课程思政下高等数学教学案例的设计与实践
孙 蕾, 朱健民, 苏 芳
(1.中山大学系统科学与工程学院,广州 510006; 2.国防科技大学文理学院数学系,长沙 410073)
1 引 言
2016年12月7日,习近平总书记在全国高校思想政治工作会议上强调,要坚持把立德树人作为中心环节,把思想政治工作贯穿教育教学全过程,实现全程育人、全方位育人,努力开创我国高等教育事业发展新局面.2020年5月28日,教育部印发《高等学校课程思政建设指导纲要》,指出全面推进课程思政建设是落实立德树人根本任务的战略举措.高等数学教学中如何渗透课程思政已经引起高校数学教学的重视与思考[1].全国高校也积极响应,将结合当前的疫情时政,采用多种教学方式,将“思政”元素融入到微积分教学之中[2].落实课堂教学中大学数学课程思政的途径很多,包括师德师风建设、挖掘课程思政元素、丰富数学文化内涵、更新教学手段、构建连接第一课堂与第二课堂的课程思政平台等[3-4].本文着重探讨了课程思政具体的实施途径,研究将高等数学思政教育与案例式教学法相融合的教学模式,并给出相应的教学案例设计.
高等数学是高校理工科学生的公共基础必修课程,它为学生将来课程学习和科学研究打下理论基础.高等数学衔接了高中数学知识与大学理工科专业知识的学习,承担了从传统知识为主到创新思维训练的转换,是理工科学生在大学一年级最重要的课程之一.高等数学的教学会对学生从高中生到大学生的转变产生深刻的影响.将思政元素融入高等数学的课堂教学,对培养学生正确的世界观和价值观,激励学生自觉把个人的理想追求融入国家和民族的事业有着重要的意义.
教学案例法是一种特定的教学方法,即在教师的指导下,根据教学目的的需要,采用案例来组织学生们进行学习、研究、锻炼能力的方法.案例式教学,以引导学生分析问题为出发点,综合利用所学知识,发挥想象力,解决实际问题.学生在分析问题、解决问题的过程中,由认知客体转变为认知主体,在科学探索中得到自我提升.成功的教学案例能驱动学生的好奇心,对探究问题产生浓厚的兴趣.在案例式教学中,教师通过选取知识点明确的案例作为高等数学课程设计对象,将问题凝练后,引导学生学会逐步分解难点、化难为易,在纷繁复杂的现象中探寻抽象的数学本质,构建新的知识结构,完成课程教学.因此,案例式教学在培养学生数学思维、提升综合能力和激发创新意识中都能发挥重要作用[5-6].
高等数学课程中优秀案例的选取如果既紧贴思政教育,又凝练了明确的教学内容的知识点,就能在提高学生思想水平、政治觉悟、道德品质的同时,激发学生的学习热情,学生顺利进入课程的情境,完成知识点的学习.教师也从知识的传授者转变为学生学习的激发者、组织者和引导者,培养学生观察世界、分析问题和解决问题的能力.将课程思政与案例式教学相结合,将达到一举多得的效果.
本文所涉及的这些案例选材具有鲜明的时代感,将数学课程的知识点与国家重大工程建设、最新科技发展前沿、社会生活热点紧密结合,实现传授知识与思政教育的高度融合.思政案例的更新和完善不仅取得了较好的教学效果,同时支持作者所在教学团队获得了多项教学比赛奖项.
2 高等数学课程思政案例
2.1 将国家重大工程与课堂教学相融合,培养学生的历史使命感
微积分理论是伴随着社会生产的创立与发展的,已经渗透到航空航天、材料、力学、控制、动力学各个领域.可以收集与国家重大工程密切相关的案例,与高等数学教学深度融合.例如,反常积分概念的引入就与航天器发射密不可分.
2020年12月17日,嫦娥五号携带月球样品在预定区域安全着陆,实现了中国航人“九天揽月星河阔,十六春秋绕落回”的伟大梦想.探月工程的“绕、落、回” 三步走战略规划是指:发射卫星绕月球旋转;月球车在月球上软着陆;携带月球样本返回地球.那么在设计探月器发射的燃料和动力时,会遇到如下问题:
例1从地球表面垂直向上发射质量为m的航天器, 当航天器距离地面h时, 求克服地球引力做的功. 如果航天器要脱离地球引力范围, 求航天器克服地球引力做的功.
解设地球半径为R,质量为M,物体与地面垂直距离为x,如图1所示.根据万有引力定律,当航天器离开地球表面高度为x时,它所受地球的引力为
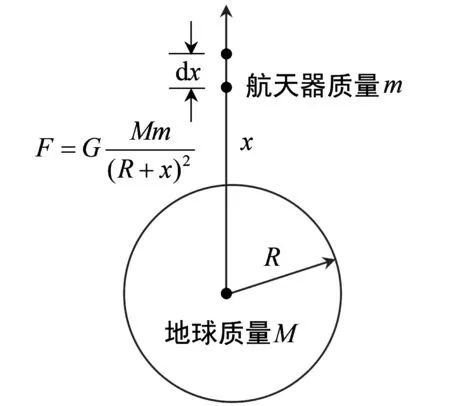
图1 航天器克服地球引力做的功
当航天器上升时,克服引力所做功的微元为
当航天器自地球表面x=0上升到高度x=h时,需要做的功为
求航天器要摆脱地球的引力所作的功,相当于在无穷区间[0,+∞)上积分,让积分上限h→∞,故有
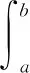
2.2 将最新科技发展与课堂教学融合,培养学生勇于创新的科研精神
在教学中融入与国计民生、社会生活息息相关的最新科技,会让学生深刻体会到数学在科技创新中的力量,激发学生投身科技研发的热情.下面以傅里叶级数为例,介绍如何将思政素材与案例式教学融入课堂教学.
没有任何学术和工程实践背景的一年级本科生是难以理解为什么要把函数展开成复杂的傅里叶级数的,然而傅里叶级数形式上的复杂给信号处理带来了极大的便利.课堂上,可以从5G技术引发激烈的中美对抗,导致美国政府制裁中兴和断供华为说起.那么为什么5G技术会引发如此呢?在信息高速传播的社会里,5G技术最具备竞力的优势就是超高速,它与其核心数学工具傅里叶分析密不可分,从而引出教学知识点——傅里叶级数.该案例通过燃情的开场白打开学生探究傅里叶级数的好奇心,用最新科技的代入感将学生的注意力很快吸引到教学内容上来,进入教学情境.
在工程上,简谐振动是最简单的周期运动,于是希望能把一切周期运动,都分解成了一系列简单的简谐振动的之和.将这种思想运用到周期函数的表示上,便产生了傅里叶级数,进入正式知识点讲授环节.完成了傅里叶级数的理论讲授内容后,再回到前面提出的问题.为什么傅里叶变换会使信号处理和传输的速度加快?
要在时间轴上表示一个复杂的无限信号,代价非常大.把信号进行傅里叶分解,就是把信号用无限项三角函数的线性组合来表示

以三角函数的角频率为自变量,傅里叶系数的模作为每个角频率对应的值,可以把信号从时域转化到频域中去,如图2所示.于是时域内无限的连续信号,就可以用频域内的离散信号表示.同时数学上可以证明当n→∞时, 傅里叶系数an→0以及bn→0.于是可以将后面足够小的项进行截断.这样复杂的时域内无限的信号变换到频域内后只用几个离散的点就能表示出来,在频域内有效地压缩信号,从而提高了信号处理的速率.这就是傅里叶变换成为重要信号处理工具的原因.表1给出了信号在时域与频域中的比较.

图2 傅里叶级数展开的示意图

表1 信号在时域与频域中的比较
2.3 将社会生活与课堂教学融合,培养学生观察世界、分析和解决问题的能力
有些数学概念的提出是源自于生产生活的需要的.将这些例子引入课堂教学,培养学生用数学思维观察世界、分析和解决问题的能力.

图3 铁轨弯道与直接连接设计的问题
比如,中国高铁历经25年从无到有的快速发展,国内运营里程已经突破2万公里,居世界首位,让国人引以自豪.如果把高铁轨道的弯道抽象成曲线,在实现弯道的设计中,常会遇到这样一个问题:一条直线的轨道,与圆弧形轨道相连接.最容易想到的连接方式就是直接将圆弧与直线相切连接.这样的设计真的能够实现列车在轨道上平稳转弯吗?
为了解决这个问题,需要引入一个刻画曲线弯曲程度的量,这就是曲率.学生带着这个问题学习曲率的概念、定义和计算方法.解决了知识点的讲授后,可以回到最开始提出的火车轨道设计的问题上来,铁轨圆弧形的弯道究竟能不能与直道直接相切地连接起来.由力学知识,物体所受的向心力与运动轨迹的曲率成正比,与速度的平方成正比.高铁在直道上高速行驶没有向心力,在圆弧形的轨道上有巨大的向心力.如果将直道与弯道直接连接,在切换轨道的一刻,会突然受力冲击.为保证高铁的平稳运行,工程上不能将直道与圆弧弯道直接相接,而必须在直道和弯道间接入一段缓和曲线.我国常使用三次抛物线缓和曲线.根据缓和曲线的设计原则,首先,缓和曲线的曲率必须是连续的,这样才能保证曲率连续地变化.其次,缓和曲线在直道与弯道的接头处的曲率要相等.在保证这两个原则的前提下,给出思考题,让学生自己设计合理的缓和曲线.至此完成案例教学的首尾呼应,培养学生自己动手动脑,用数学思维解决社会生活中的实际问题的能力.
2.4 将民族自豪感与课堂教学紧密结合,培养学生爱国主义精神
早在春秋时期,庄子在《天下篇》中提到的“一日之槌,日取其半,万世不竭”就是极限思想的最初萌芽.魏晋时期的数学家刘徽首创割圆术,刘徽在《九章算术》提到“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”割圆术用积分的思想计算圆的面积,为计算圆周率建立了严密的理论和完善的算法.南北朝时期的祖冲之利用割圆术将圆周率计算到小数点都第七位,这一记录在世界范围内保持领先了近一千年.这些例子,足以让我们为祖先的智慧所折服,爱国主义情怀油然而生.
例2如图4所示,利用割圆术的思想计算半径为r的圆的面积.
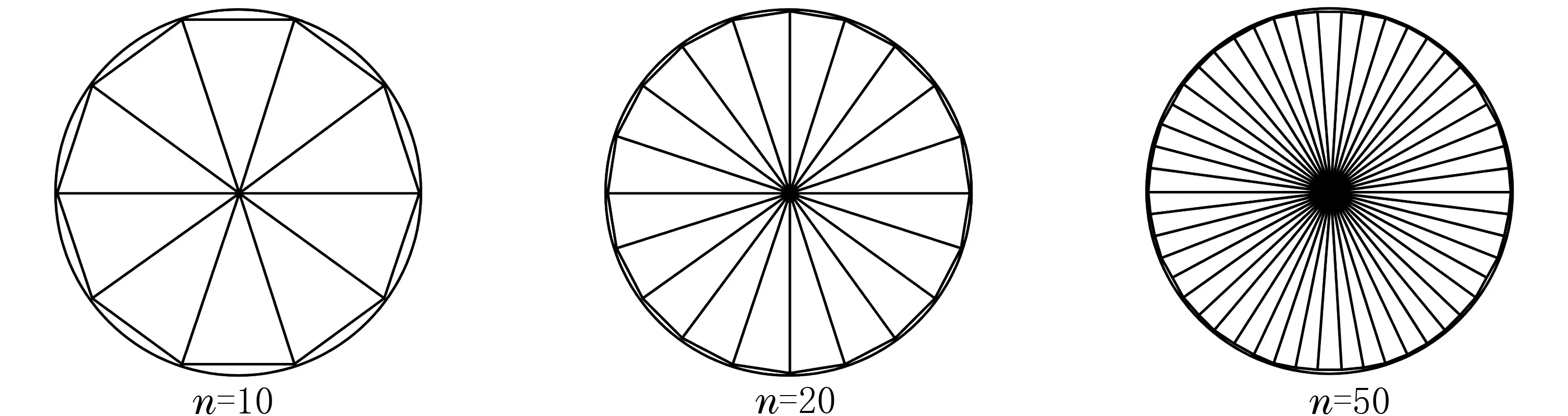
图4 “割圆术”的思想
解圆内接正n边形的面积为

圆的面积为

2.5 将数学文化与课堂教学紧密结合,提升学生的审美素养

身边常有一些和数学知识紧密联系的案例,能完美地诠释数学的和谐美、对称美、简单美和抽象美.这些案例能充分体现数学文化,提升学生的审美素养.
在高等数学[7]的作业题中可以证明,两条不垂直的异面直线,取其中一条做轴,另一条直线绕其旋转,得到的图形是单叶双曲面(图5).广州市地标建筑广州塔也是直线钢柱倾斜交织而成,它的设计理念由荷兰设计师海默尔提出:将橡皮筋绑在两个椭圆片之间,拉直,轻轻旋转,一个奇妙的几何结构就产生了(图 6).把圆换成椭圆,扭动后产生的结构宛如少女的腰肢,优雅而妩媚,因此广州塔又名“小蛮腰”(图7).标准的单叶双曲面水平截面是同心的椭圆,且主轴平行,而广州塔的水平截面是主轴依次旋转的椭圆,错落有致,让人产生空间扭转的迷人错觉.那么它用直线交织而成的外表面是还是单叶双曲面吗?如果不是,又如何建立它的曲面方程?(该方程的求解见参考文献[8])学生在探求这些问题的时候,既加深了知识点的掌握,又体验到用不同的方程曲面形态,展示不同的建筑之美,表达设计师不同的情感与理念.
地标建筑能反映出城市的文化内涵,通过介绍著名的地标建筑的设计将数学与建筑设计之美相结合,加深学生对曲面方程的理解.课堂上可以采用该案例教学,层层深入地剖析问题,通过师生之间的对话和交流,层层递进地将简单的曲面方程求解问题推广到更一般的情形,调动学生了探究、求解问题的欲望,并使学生感受思考的乐趣.
3 教学效果
为了解在高等数学教学中采用案例教学法融入课程思政教育的教学效果,设计了一份电子匿名调查问卷发放给最近一轮高等数学教学班的学生,共收到398份有效问卷。问卷问题及调查结果如图8所示. 从调查问卷反馈的结果来看,学生给出了积极的反馈信息.大多数学生认可将思政教育引入高等数学课堂的必要性,并乐于接受这种课堂学习模式的.其中,最受欢迎的教学案例类型是将国家重大工程与课堂教学相融合,培养学生的历史使命感,这也启发教师平时要多关心国家大事,主动收集素材并挖掘提炼蕴含的德育元素,将其融入教学案例设计,贯穿到高等数学课程教学实践中去.
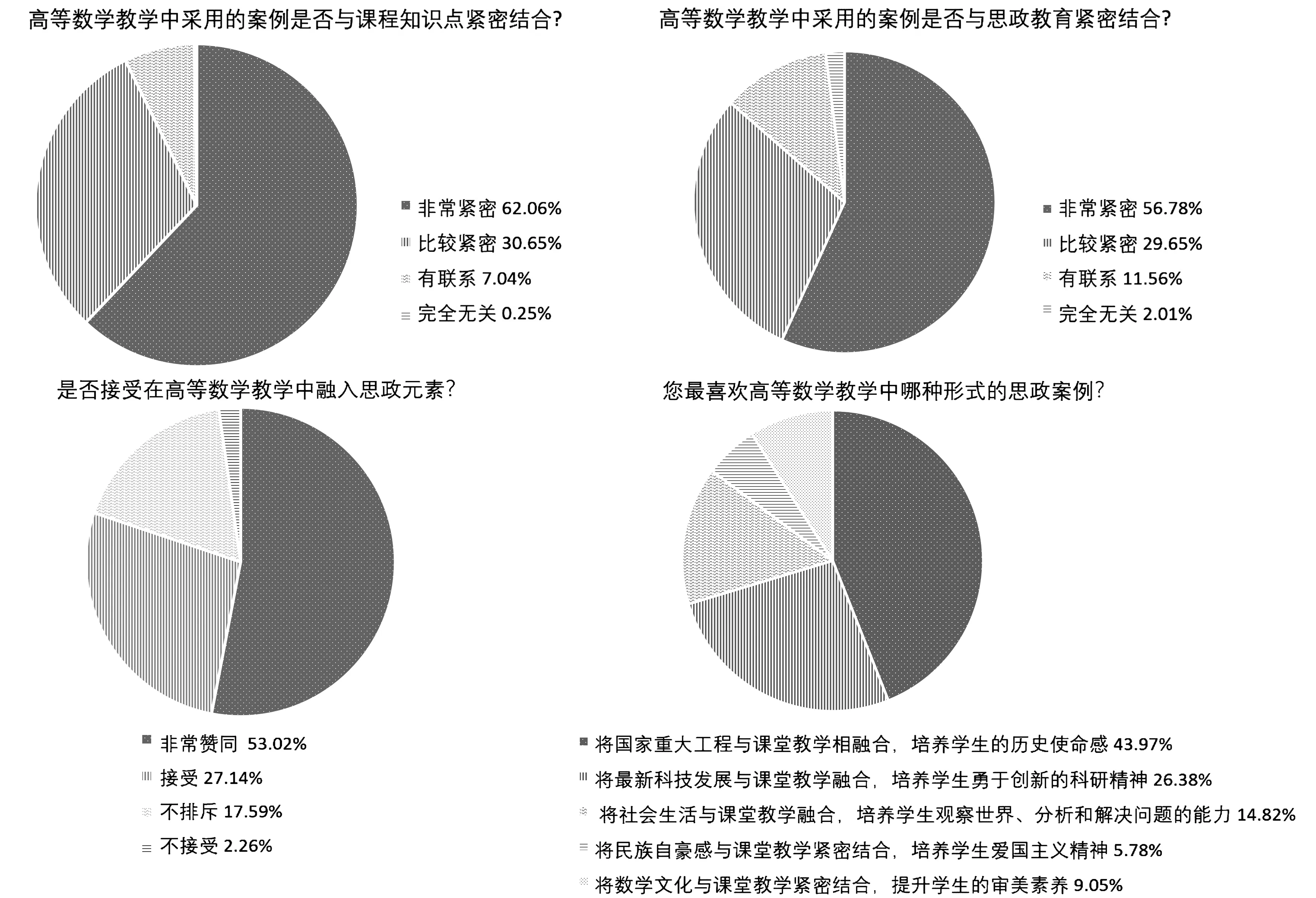
图8 调查问卷和反馈结果
学生在问卷调查中诚恳地给出了自己关于课程思政下高等数学教学案例的设计的想法,图9截取其中部分交流信息,其中既有对高等数学中思政教育的肯定,也有非常中肯的建议和意见。

图9 学生交流关于高等数学中思政教育案例的心得体会
本文全体作者最近一次高等数学教学的教务系统学生评价的分数均超过98分,具体情况如表2所示.学生对在高等数学教学中采用案例教学法融入课程思政教育是持肯定态度的.在思政教育的同时,也提高了学生对学习高等数学的积极性,获得了预期的教学效果.

表2 教务系统学生评价
在高等数学教学中采用案例教学法融入课程思政教育不仅得到了学生的认可,还得到高校同行的肯定.高等数学课程思政案例的更新和完善支持国防科技大学高等数学教学团队先后获得了全国高校数学微课程教学设计竞赛全国一等奖三项,湖南省普通高校教师课堂教学竞赛一等奖三项,军队院校数学创新教学比赛一等奖两项,军队院校数学微课程教学设计竞赛一等奖一项.教学案例《单叶双曲面与现代建筑》获得广东省本科高校课程思政优秀案例二等奖.
因此,为高等数学课程精心设计的教学案例,既能激发学生探求知识的欲望,又将思政教育融入了课堂,这种教学模式得到了学生和同行的一致认可.
4 结 论
在高等数学课程的教学中,成功的教学案例能驱动学生的好奇心,对探究问题产生浓厚的兴趣.案例式教学能将复杂的数学知识融入具体案例,构建新的知识结构,对培养学生数学思维,提升综合能力和激发创新意识都有巨大的帮助.思政素材将国家重大工程与课堂教学相融合,既能培养学生的社会责任感,又能培养学生用数学思想解决实际问题的能力.平时应关注时事,留心生活,遇到好的教学案例和思政素材要及时收集并整理,真正做到:用心浇灌,立德树人,一切以学生为本;时光打磨,日积月累,春雨润物细无声.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.

