基于B样条混合模型的一维形状分析
邵周健, 王旭辉
(合肥工业大学数学学院,合肥 230601)
1 引 言
信息几何主要研究概率分布族所具有的微分几何结构,在研究流形和度量空间上的形状分析时常常用高斯混合模型来表示形状.参考文献[1]中用地标点表示每个形状,并将形状建模为高斯分布的混合,高斯混合模型是由k个高斯模型组合而成.然而,高斯混合模型中的高斯函数是超越函数,且不具有局部支撑性,当运用高斯混合模型进行形状分析时,通常无法得到显式表达式.参考文献[2]提出了用熵度量计算信息矩阵的方法,并计算出其显式表达式,但是由于高斯函数的性质,测地线距离的计算成本较高.参考文献[3]中通过估计两种密度函数之间的测地线距离,得到形状之间的相似性度量.然而,该方法求出的距离显式表达式仅仅适用于特殊的高斯混合模型.流形上测地线的构造还可以使用射击法[4-5],基于微分方程的梯度下降方法[1],基于变分函数的梯度下降方法[6-7].综上可知,运用高斯混合模型进行形状分析的两个主要缺点为:(i)度量没有显式表达式;(ii)梯度的估计较复杂.
近期Strait等研究了弹性形状分析和基于地标约束的弹性形状分析,将形状的整个轮廓纳入计算,在处理复杂形状时具有一定的优势[8-9].然而,要实现对平移、缩放、旋转和重新参数化不变的形状分析相对困难.例如,参考文献[10]提出了用坐标下降法来解决再参数化问题.
针对高斯混合模型在形状分析上的不足,本文拟建立一种基于B样条函数的形状表示模型.通过研究B样条模型情形下的形状度量,进而获得不同形状间的测地线及测地距离.由于B样条函数是分段多项式且具有局部支撑性[11],使得测地线及其距离的计算数值较为稳定.特别地,如果对B样条模型的节点做恰当限制后,所得到的信息矩阵具有显式表达式,使得计算更为高效.
2 B样条模型
高斯混合模型是由k个单高斯模型组合而成,令μ1,μ2,…,μk∈为形状的k个地标点,所有的这些地标被视为一个单一向量θ=(μ1,μ2,…,μk),高斯混合模型为
(1)
其中σ2为方差.因此,具有k个地标点的形状被表示为k个分量高斯混合模型.然而,当应用高斯混合模型进行形状分析时,信息矩阵一般不具有显式表达式且计算成本高[1],因此希望寻找其他的函数代替高斯函数.
B样条在工业中广泛应用于构造形状曲面[12],1992年,Unser等人证明了当样条n的阶数趋于无穷时,B样条收敛于Lp(),∀p∈[2,+∞)中的高斯函数.此外相关数值计算结果还表明,三次B样条基函数可较好逼近高斯函数[13].
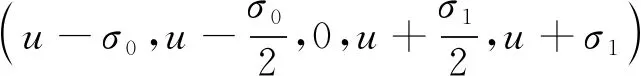
(2)
由(2)式知,N(x)具有局部支撑性(如图1所示),即N(x)在区间上(u-σ0,u+σ1)是非零的.因此,可将N(x)记为N(x;σ0,σ1),其中σ0,σ1是控制非零区间大小的缩放参数,图2中展示了N(x;σ0,σ1)在不同参数下的情况.
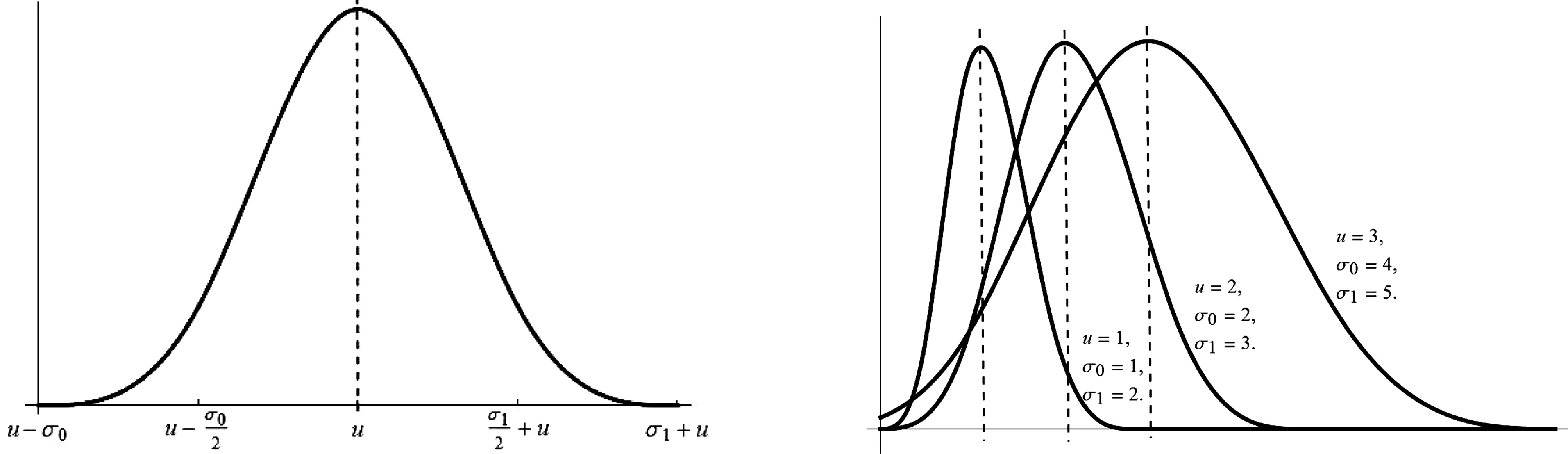
图1 三次B样条基函数N(x;σ0,σ1) 图2 不同参数下的三次B样条基函数
基于N(x;σ0,σ1)可定义B样条混合模型.给定k个地标点u1,u2,…,uk∈,其对应的B样条混合模型为
(3)
其中wi为第k个B样条基函数的权重,用来平衡第k个地标点对模型的影响,σi0,σi1用于控制相邻地标点之间的影响.该B样条混合模型可以用来表示形状分析,图3为有五个地标点的B样条混合模型,在图3-1中取σi0=σi1=2,ui=i,再将各个地标点的权重分别取为w1=0.20,w2=0.27,w3=0.117,w4=0.002,w5=0.411,图3-2中σi0=ui-ui-1,σi1=ui+1-ui,权重分别取为w1=0.17,w2=0.32,w3=0.22,w4=0.17,w5=0.12.
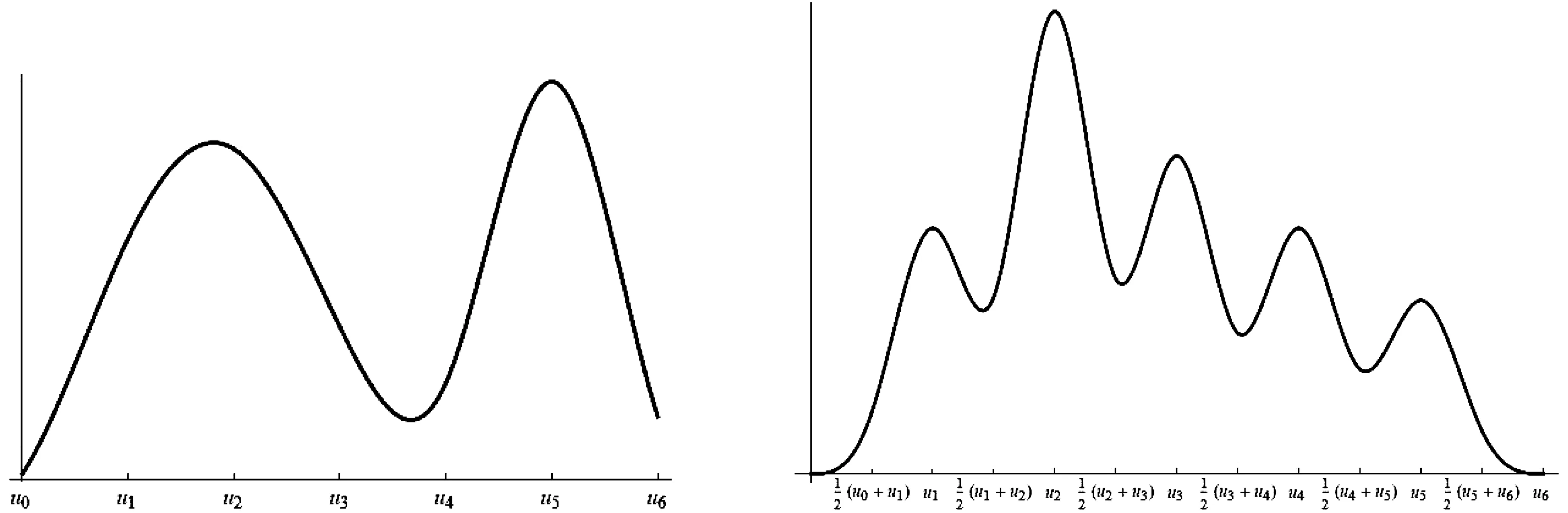
图3-1 图3-2
3 形状度量
上节阐述了基于B样条混合模型的形状表示法,本节主要讨论如何利用概率模型来度量形状之间的差异.在信息几何中,概率模型p(x;θ)可视为对应黎曼流形上的一个点,而信息矩阵g(θ)被认为是参数空间上唯一的黎曼结构.参考文献[14]中首次证明了Fisher信息矩阵满足黎曼流形上度量,Fisher信息矩阵的(i,j)项是由Fisher-Rao度量得到

(4)
因此,对于两个具有有限个地标点的形状,基于高斯混合模型的形状表示能度量它们之间的差异,混合模型表示已被用于解决各种形状分析问题[15-16].然而,Fisher-Rao度量有一个基本的缺点:对混合模型来说度量没有显式表达式.因此,需要对(4)中的积分进行数值计算,这就导致了该模型在计算上的复杂性.为了解决这个问题,参考文献[2]提出了一种熵度量:
(5)
且由黎曼度量(5)诱导出来的信息矩阵具有显示表示式,所以在求测地线时使用熵度量提高了计算效率. 本文也采用熵度量来计算了基于B样条基函数的信息矩阵,并且在计算时可采用高斯数值积分[17],该方法可加快计算速度且提高精度.特别地,取σi0=ui-ui-1,σi1=ui+1-ui时,可由相关符号计算软件计算出度量矩阵gij的显式表达式.
注 具体表达式见https:∥note.youdao.com/s/6EEfL8Hp.
4 测地线计算
设θ(t)=(θ1(t),θ2(t),…,θK(t)),t∈[0,1]是流形上的一条光滑路径,则该路径的长度为
(6)
定义θ(t)的能量泛函为
(7)
给定流形上两点P和Q,对于流形上连接两点的所有分段光滑路径,式(6)具有与式(7)相同的最小值[18].因此,连接P和Q的黎曼流形上的测地线是该能量泛函的极值点,测地线距离就为由连接这两点的所有分段光滑路径的最小长度(即能量泛函的最小值).
(8)
设流形上的P点为形状S0、Q点为形状S1,连接两点测地线上的每一点对应了S0与S1之间的中间变形形状.
关于测地距离的求法,许多文献里都有所研究,在参考文献[3]建立高斯模型后,在两种特殊情况下将Fisher距离与庞加莱半平面距离做相似变换求得了距离的显式解.对于混合模型,参考文献[19]提出测地距离可用打靶法求出,该方法是用离散化数值步骤求出测地线微分方程边值问题在离散点上的近似解.此方法要求求得边界点对应的参数,但困难在于该参数是未知的.配置算法是求解带边界条件常微分方程的常用方法[20],通常比打靶法更稳定,但可能需要更多的计算.此外,参考文献[21]还研究了一类步数为2(k+1)的次黎曼流形上的测地线.
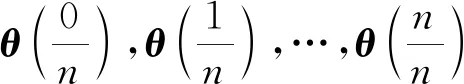
(9)
(10)
5 数值实例
本节基于第3,4节中用B样条模型来表示形状的相关结果,用一些模拟采样数据做数值实例.例1,2分别选取有不同数量的地标点形状,用B样条混合模型表示该形状,求出初始形状S0到目标形状S1的测地线距离及变形过程,并与基于高斯混合模型的形状变形过程进行了对比.
例1选取三个地标点u1,u2,u3用B样条混合模型表示形状,取
σi0=ui-ui-1,σi1=ui+1-ui,
地标点个数LN及权重wi选取的数据见表1,变形中间步骤为5,求得的测地线距离见表2,且由初始形状向目标形状的变化过程如图4所示,该变形过程与基于高斯混合模型的形状变形过程相似.

表1 地标点及权重数据(LN=3)

表2 测地线距离数值
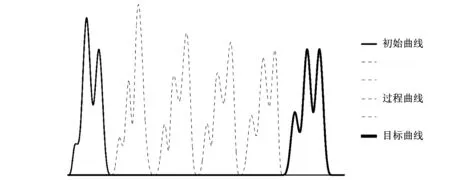
图4 变形图 (LN=3)
例2给定五个地标点u1,u2,u3,u4,u5用B样条混合模型来表示形状,并取
σi0=ui-ui-1,σi1=ui+1-ui,
表3是地标点个数LN及权重wi数据的选取,变形中间步骤为5,求得测地线距离见表2,其由初始形状向目标形状的变化过程如图5所示,该变形过程与基于高斯混合模型的形状变形过程相似.

表3 地标点及权重数据(LN=5)
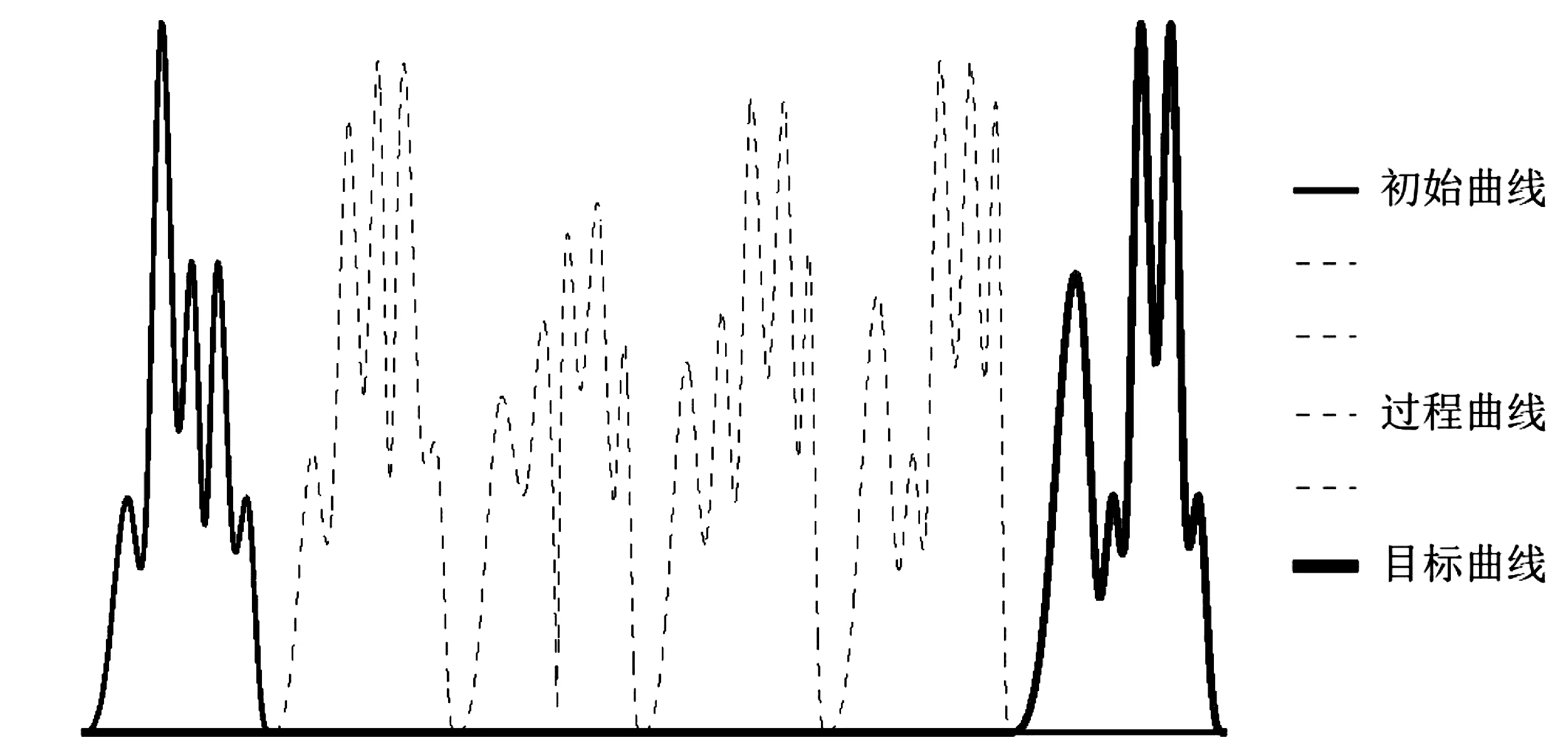
图5 变形图 (LN=5)
6 结 论
提出了一种计算流形上形状之间距离的方法,它是基于B样条混合模型的特殊的形状表示.在明确了B样条基函数与高斯函数的关系后,选择好节点序列求得对应的B样条基函数,并建立B样条混合模型,利用熵度量导出了信息矩阵的显式表达式.最后求得黎曼流形上两点间测地线距离,即形状之间的距离.另外,还应用此模型做了形状之间的变形,并与传统高斯混合模型进行计算效率上的对比,展示了该模型的有效性.
尽管基于高斯混合模型表示的形状分析已经得到了广泛的研究,但相应的信息矩阵通常无法求得显式表达式,在测地线计算上也需要较高的计算成本,且数值具有不稳定性.通过用B样条函数代替高斯函数,本文提出了一个新的概率模型来表示形状.由于B样条函数是局部支撑的,运用B样条模型表示形状并计算形状之间的测地线是成功有效的,也给出两个计算测地线距离的数值实例来证明本文方法的有效性.与传统的高斯模型表示相比,所提出的新模型表示显著降低了计算成本.由于本文关注一维计算的可行性,二维情况的具体应用将在未来进行研究.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.

