基于Weibull模型的混凝土冻融损伤寿命预测及应用

杨冬鹏，郭卫民，王宝民

(1.辽宁省水利水电勘测设计研究院有限责任公司，辽宁 沈阳 110006；2.辽宁省交通规划设计院有限责任公司，辽宁 沈阳 110166；3.大连理工大学 土木工程学院，辽宁 大连 116024)

1 研究背景

混凝土作为当今应用最广泛、最重要的一种人造建筑材料，其耐久性能直接影响着工程的使用寿命。混凝土耐久性受内外部因素的共同影响，其中内部因素主要有混凝土组成材料用量、材料性质及微观结构[1]；外部因素主要是指其服役环境包括应力条件、温度湿度条件等各种外部因素[2-4]。不同环境条件下，各影响因素造成的影响权重大不相同。对于我国北方严寒和寒冷地区，混凝土的抗冻性能是影响混凝土服役寿命的关键因素。目前基于冻融损伤作用下的混凝土损伤模型研究已取得一定研究成果[5-6]。宋玉普等[7]基于三参数Weibull分布建立了一种混凝土结构冻融损伤可靠度分析模型，并利用等效损伤原理推导了计算混凝土冻融损伤失效概率及剩余寿命计算公式；关宇刚等[8]结合可靠度与损伤理论，提出了适用于不同边界条件以及包括单因素和多因素复合作用下的混凝土寿命预测多元Weibull分布模型；余红发等[9-10]基于Fick第二扩散定律建立了多种因素作用下的混凝土氯离子扩散理论模型，解决了Fick扩散理论在混凝土中的适应性问题。不同的科研工作者对于表征混凝土冻融损伤程度的指标选取各不相同，依据不同的选取指标主要有基于冻融损伤过程的质量衰减模型、相对动弹性模量衰减模型、强度衰减模型、能量耗散模型、超声波声速变化规律模型等。

目前对于混凝土冻融破坏过程的认识基本一致，即认为混凝土冻融损伤破坏过程是混凝土内部微单元体在膨胀压力和渗透压力两种破坏应力的作用下逐渐破坏失效的过程。Weibull理论是一种广泛应用于各种寿命试验的可靠性分析和寿命检验的理论。研究表明[8]，Weibull分布同样可以较好的应用于模拟混凝土冻融损伤及寿命预测。

物理模型的建立对冻融损伤模型的准确性至关重要，目前常见的对混凝土结构的损伤模型和寿命预测模型多是以半无限空间体为物理模型，而基于冻融损伤的寿命预测多以混凝土快速冻融试验(棱柱体试件)所得结果为物理特征指标，必然会因为物理模型与实际状况存在的差异而导致最终结果产生一定误差。因此，为了能够准确预测既有混凝土构筑物的使用寿命，本文以冻融损伤理论为基础，研究以水工混凝土棱柱体抗冻试件为物理模型的冻融损伤模型和寿命预测方法，建立基于Weibull模型和混凝土快速冻融试验的混凝土冻融损伤模型寿命预测方法，并通过室内试验和实际工程案例进行验证。

2 模型的建立

2.1 模型的引入及说明将Weibull分布模型应用于混凝土冻融损伤模拟和寿命预测中，有三个基本假设[10-11]，如下：

(1)假设混凝土内部是均匀连续的，当混凝土四周边界处于同一环境条件时，混凝土内距离边界最小距离的部分均服从同一种损伤演变规律。

(2)混凝土损伤过程是混凝土内部微缺陷随龄期逐渐增多、积累的过程。若将混凝土看作是大量微“元件”的聚合体，则混凝土内部微“元件”失效率是随时间的递增函数，符合形状因子大于1时的Weibull分布函数。

Weibull三参数分布函数表达式如式(1)：

F(t)=1-exp{-[λ·H(t-t0)]α}

(1)

式中：t为时间；t0为阈值；λ为尺度因子；α为形状因子；H为Heaviside函数(当t-t0≥0时，H=1；当t-t0<0时，H=0)。

(3)假设混凝土内部为均匀的，则根据Weibull分布特性，可认为混凝土内部各点失效曲线形状一致，即形状因子α一致。尺度因子λ表征混凝土对不利条件的抵抗能力大小，该值越大，混凝土抵抗能力越小；该值越小，抵抗能力越大。尺度因子越大表明材料抗力越弱，阈值出现的越早；反之，阈值出现的越晚。因此，可假设尺度因子λ与阈值t0成反比例关系，见式(2)，k0为比例系数：

t0=k0·λ-1

(2)

2.2 基于标准长方体冻融试块的模型推导混凝土内某点失效尺度因子是与此点在混凝土中的位置(深度)有关的，即式(3)

λ(x,y,z)=λ(|x|,|y|,|z|)

(3)

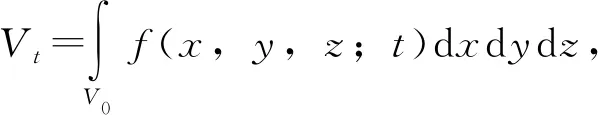
根据损伤理论得损伤度D=Vt/V0，可得出混凝土试块在t时刻的损伤因子D，见式(4)。

(4)

因为在SL/T 352—2020《水工混凝土试验规程》中，进行快速冻融试验的试样尺寸为100 mm×100 mm×400 mm，是尺寸比为1∶1∶4的长方体。因此在本文中，对1∶1∶4的长方体混凝土冻融试件进行如图1所示的网格划分，长方体长边划分为4N份，宽、高边划分为N份，设N为偶数；图1中G表示损伤梯度。通过计算推导得到距离混凝土试件表面最短距离相同的第i层(阴影部位)的单元数Ni见式(5)：

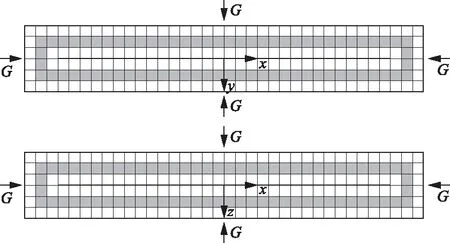
图1 模型网格划分示意

Ni=18N2-48iN+24i2-24N+24i+8

(5)

式中i=0，1，2，…，(N/2-1)。

微单元发生破坏随时间发生的分布函数为F(t)，则第i层单元破坏为Fi(t)。t时刻第i层单元破坏Ni块这一事件Φi的数学期望为式(6)和式(7)。

E(Φi)=Ni·Fi(t)

(6)

(7)

假设尺度因子λ沿截面呈非线性变化，其第i层的尺度因子λi为式(8)。

λi=λ0+ν·(i+0.5)-1

(8)

式中：λ0为待定的均匀尺度参数；ν为待定的梯度因子；i=0，1，2，…，(N/2-1)。

则时刻t全部单元破坏的数量为式(9)。

(9)

代入式(4)中可得整个模型的冻融损伤因子D如下：

(10)

式中λi为第i层的尺度因子。

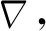
(11)

式中yi为混凝土损伤度的实测值。

(12)

(13)

(14)

(15)

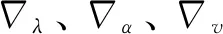
3 模型的应用

3.1 冻融作用下混凝土损伤度定义处于寒冷与严寒地区的混凝土结构，混凝土内部水分会伴随着环境温度的变化不断处于冻结-融化的过程中，经过多次冻融循环后，混凝土某些物理力学性能会发生明显的变化[12-13]。这些物理力学特性参数变化也就成为衡量混凝土冻融损伤程度的尺度，常用的物理力学特征参数包括质量损失率、强度损失率、相对动弹性模量等。混凝土抗冻性的失效判断常用指标多采用相对动弹性模量和质量损失率，本文选择相对动弹性模量用于损伤度的定义。由损伤力学理论可知，冻融损伤下混凝土的损伤度可定义为：

D=1-Pn

(16)

式中Pn为混凝土n次冻融循环后的相对动弹性模量。

3.2 试验结果及讨论为了验证模型是否能准确反映出标准抗冻试块的冻融过程，按照每立方混凝土中水泥∶水∶砂∶卵石(5～20 mm)∶卵石(20～40 mm)∶减水剂=405∶158∶580∶492∶739∶4.0的配合比制备了标准长方体抗冻试块并进行了快速冻融循环试验，试验结果见表1。

表1 验证混凝土试块抗冻试验结果

应用建立的模型对表1的试验结果进行计算，其中网格划分层数N为人为设定。网格划分对数据计算的准确性有着重要的影响，网格划分的越细，划分层数越大，所得结果误差越小。经计算验证，当网格划分为20层及以上时，计算误差已满足精度要求，因此，这里选取网格划分层数N为20层。通过计算得到4个模型参数λ0、ν、k0、α分别为2.62、0.42、0.003、3.49。冻融损伤理论预测值和实测值的比较如图2。试验结果表明，建立的冻融损伤模型预测值和实测值基本吻合，说明此模型能够较好的描述混凝土冻融损伤破坏过程。

图2 冻融损伤理论预测值和实测值比较

4 基于冻融损伤的混凝土寿命预测应用

4.1 基于冻融损伤的混凝土寿命预测过程与室内快速冻融循环试验不同，实际服役环境中影响混凝土寿命的因素是非常复杂的，对混凝土寿命影响较大的因素包括环境温度变化、湿度变化、盐类浓度、荷载、外物冲击等[14-16]。然而，考虑多因素耦合作用下的室内试验难以实现，这里仅考虑了混凝土的冻融损伤进行室内加速试验，进行混凝土寿命预测，具体方法和步骤如下：

(1)调研混凝土配比，制作同配比标准混凝土抗冻试块，进行冻融循环试验，得到混凝土损伤和冻融循环之间的关系，确定混凝土试块室内冻融损伤模型。

(2)建立混凝土在实验室的加速试验损伤度与实际工程环境中混凝土损伤度的关系。在式(16)基础上，加速试验和现场实际环境中混凝土的劣化成比例关系，假定加速试验混凝土到达寿命时的损伤程度同实际混凝土到达寿命的损伤程度相同。对于未有工程现场损伤资料的，可根据经验对加速系数K取值，一般在1∶10～1∶15之间[11，17]，由此能够从加速试验寿命方便得到实际寿命。对于已运行使用的混凝土结构，可对混凝土结构进行检测，以获得运行期间较真实的加速系数K，结合室内加速试验结果预测混凝土结构的实际寿命。

由于混凝土冻融损伤度是对于试件(结构)初始状态而言的，因而现场混凝土芯样的快速冻融试验结果并不能直接用于计算现场混凝土的损伤度。同样，混凝土冻融破坏终止条件(《水工混凝土试验规程》(SL/T 352—2020)中相对动弹性模量下降至初始值的60%或质量损失率达到5%)是相对于混凝土试件(结构)初始时的状态。因此，现场混凝土芯样和室内混凝土试样的终止条件并不相同。

现场取芯试样进行冻融循环得到的相对动弹性模量是针对取芯时的混凝土状态，而此时的混凝土已经经历若干年服役，已有一定的损伤。而按照配合比新成型的混凝土试件可以看作未损伤的混凝土试件。此时，现场取芯混凝土冻融循环试验时混凝土试样的动弹性模量要比新浇筑时的动弹性模量低。因此为了更为准确地确定混凝土相对于未损伤时的混凝土状态，本文设计采用迭代逼近方法。

第一次迭代：首先利用损伤模型计算出室内长方体试样和工程实体钻芯试样损伤度为0.4时的冻融循环次数，两者的冻融循环差为N1，N1对应的室内长方体试样损伤值作为工程实体的初始损伤值D1。则与室内长方体试样损伤度为0.4相对应的工程实体钻芯试样损伤度应为0.4/(1-D1)。

第二次迭代：利用损伤模型计算出工程实体钻芯试样损伤度为0.4/(1-D1)时的冻融循环次数，它与室内长方体试样损伤度为0.4时的冻融循环次数差为N2，N2对应的室内长方体试样损伤值作为工程实体的初始损伤值为D2。则与室内长方体试样损伤度为0.4相对应的工程实体钻芯试验损伤度应为0.4/(1-D2)。

同理依次进行迭代，得到稳定的循环次数差N，这个N就表征工程实体建成之后冻融损伤所对应的快速冻融次数，结合混凝土室内试验的抗冻数据即可得到工程实体的寿命预测结果。

4.2 基于冻融损伤的混凝土寿命预测应用实例石门水库枢纽工程位于辽宁省盖州市，工程始建于1970年，1971年11月基本竣工，现场照片如图3。分别在2006年5月和2016年9月对石门水库溢洪道左边墙进行钻芯取样，进行混凝土抗冻性能检测。为对此部位混凝土进行寿命预测，进行了以下工作：(1)试样制取：间隔10 a进行了两次钻芯取样，同时在室内按此部位混凝土配合比按《水工混凝土试验规程》(SL/T 352—2020)制备了长方体混凝土抗冻试件；(2)同时对现场取芯、室内取芯和室内成型试样进行快速冻融试验，测量混凝土的相对动弹性模量；(3)根据测量结果确定寿命预测模型的4个待定系数；(4)应用迭代逼近法确定现场芯样的损伤度，并进行寿命预测。

图3 石门水库溢洪道

试验部位混凝土使用的配合比为水泥∶水∶砂∶卵石(20～30 mm)=307∶172∶624∶1297，设计混凝土强度等级为C20，设计坍落度为40 mm。

将3种类型试件置于相同环境进行冻融循环试验，得到试验结果见图4。

利用式(16)确定混凝土芯样冻融循环的损伤度，从图4中的数据可以看出室内长方体试样的相对动弹性模量变化趋势同室内圆柱体钻芯试样的基本一致。运用最小二乘法确定Weibull模型(式(10))中的待定系数，结果见表2，冻融损伤理论预测值和实测值的比较如图5。

表2 4种试样待定系数计算结果

图4 4种试样快速冻融试验结果(35 a和45 a)

图5 4种试样待定系数计算结果(35 a和45 a)

从图5看出，式(10)的损伤模型对圆柱体试样仍有较好的拟合效果。由图4可以看出，工程实体的芯样由于已服役多年，混凝土已有初始损伤，所以对冻融损伤的抵抗能力较差，冻融损伤的推进速度也较快。

应用迭代逼近法处理损伤数据：第一次迭代，根据冻融损伤模型可以计算出室内长方体快速冻融试验到达破坏(损伤度0.4)时的冻融循环次数为242次，35 a时的现场钻芯试样破坏时(损伤度0.4)的冻融循环次数为152次，差值为N1为242-152=90次，90次循环对应的室内长方体试样损伤值D1为0.049，则与室内长方体试样损伤度为0.4相对应的工程实体钻芯试样损伤度应为0.4/(1-0.049)=0.421，对应的冻融循环次数为155次。

第二次迭代，现场实体钻芯试样和室内长方体试样损伤时冻融循环差值N2为242-155=87次。N2对应的室内长方体试样损伤值D2为0.045。则与室内长方体试样损伤度为0.4相对应的工程实体钻芯试样损伤度应为0.4/(1-0.045)=0.419，与第一次迭代冻融循环次数对应的155次较为接近，迭代结束。

则运行的前35 a中，每年的冻融损伤等同于室内经历快速冻融次数为87/35=2.49次，35 a时的混凝土寿命预测为155/2.49=62.4 a，混凝土总寿命周期为97.4 a。

同样步骤处理45 a时的钻芯试件冻融数据可以得到，45 a的冻融使混凝土的损伤度为0.072，每年的冻融损伤等同于室内经历快速冻融次数为114/45=2.53次，45 a时混凝土的寿命预测为135/2.53=53.3 a，混凝土总寿命周期为98.3 a。

考虑到混凝土的离散型和外部环境因素的变化，以及取样月份的不同，两次寿命周期预测差异0.9 a是可接受的，此预测方法较为合理。通过石门水库冻融寿命预测的结果可以看出，通过迭代逼近法获得混凝土的初始损伤状态及进行寿命预测是可行的。

5 结论

(1)将Weibull分布模型应用于混凝土冻融损伤模拟中，以混凝土标准快速冻融试件为基本物理模型，建立了一种基于混凝土快速冻融试验的损伤模型，通过室内试验验证，模型计算结果与试验结果拟合效果较好。(2)提出了一种迭代逼近的寿命预测方法，通过该方法能够快速有效地得到工程实体实际冻融损伤所对应的室内快速冻融次数，结合室内快速冻融试验结果便可对混凝土剩余寿命进行预测。对同一工程实体，间隔10 a取样进行寿命预测，两次预测总寿命周期差异为0.9 a，说明该方法应用于工程实体的寿命预测是可行的。