风光水互补系统时间序列变量概率预报框架

张振东，罗 斌，覃 晖，唐海华，周 超，冯快乐

(1.长江勘测规划设计研究有限责任公司，湖北 武汉 430010；2.长江水利委员会 互联网+智慧水利重点实验室，湖北 武汉 430010；3.华中科技大学 水电与土木工程学院，湖北 武汉 430074)

1 研究背景

风光水互补系统出力主要受径流、风速、太阳辐射强度和负荷影响，获取这四者的高精度预测结果对风光水互补系统的稳定安全运行具有重要作用。四者的共同点在于都是时间序列变量[1]，预报方法有类似之处也各有不同。

时间序列变量预测方法主要分为两大类：物理过程驱动方法和数据驱动方法[2-4]。径流物理过程驱动方法以水文学概念为基础，将流域的物理特征进行概化，并结合水文经验公式来近似地模拟流域内降雨、径流的形成过程从而完成预报过程[5]，比如新安江模型[6]和水箱模型[7]等。风速物理过程驱动方法基于温度、湿度、气压、风速等气象数据和地形数据构建数学物理方程来模拟未来一段时间某区域或全球尺度风速变化过程，例如：数值天气预报模型[8]。光伏物理过程驱动方法主要采用数值天气预报和卫星图片进行太阳辐射强度预测[9]。物理过程驱动方法的优势在于模型可解释性强，缺点在于对基础数据要求高、建模复杂、求解耗时。

数据驱动方法通常根据待预测变量的历史信息以及气象相关因子采用机器学习或深度学习等统计类方法对径流、风速、太阳辐射强度和负荷进行预测[10-13]。数据驱动方法的优点是预报速度快、预测精度较高；缺点是预报模型是黑箱模型，可解释性差，结果依赖于样本数据质量。常见数据驱动方法可以分为时间序列模型、机器学习或深度学习模型以及多模型的混合方法。使用自回归差分滑动平均(Autoregressive Integrated Moving Average，ARIMA)等时间序列模型进行预测的前提条件是数据满足平稳性假设或通过差分化处理之后满足平稳性假设[14]，该假设限制了这类算法的使用场景。为了处理变量的非线性、非平稳性和随机性等特征，许多机器学习方法被用于径流、风速、太阳辐射强度和负荷预测，比如支持向量回归(Support Vector Regression，SVR)[15-18]、极限学习机[19]和人工神经网络模型(Artificial Neural Network，ANN)[20-23]等。近几年，随着计算机技术和人工智能的蓬勃发展，深度学习模型[24]逐渐被运用于时间序列变量预测领域。长短期记忆网络(Long Short-Term Memory Network，LSTM)[25-26]和卷积神经网络(Convolutional Neural Network，CNN)[27-28]因分别擅长时序处理与特征提取而被用于径流、风速、太阳辐射强度和负荷的预测。为了克服单一预测模型的缺点，同时发挥多个预测模型的优势，混合模型逐渐成为时间序列变量预测主流方法，例如时间序列模型与机器学习模型的组合ARIMA-ANN[29]，模态分解机制与LSTM等模型的组合[30]，LSTM和CNN深度学习模型的组合[31]等。受径流、风速、太阳辐射强度和负荷不确定性特征的影响，确定性预测结果给调度决策人员提供的信息有限，概率预报正在成为预测领域的研究热点与趋势。构造一定置信度对应的上下限区间[32]来量化径流的不确定性是思路之一；更全面地，基于贝叶斯理论[33]、高斯过程回归(Gaussian Process Regression，GPR)[34]以及分位数回归结合核密度估计方法[35]的概率预报模型，可以获取径流、风速、太阳辐射强度和负荷的概率密度函数，为调度人员提供更丰富的信息。

综上所述，径流、风速、太阳辐射强度和负荷预测研究还需进一步提升预测精度、量化预报不确定性并增强预报的可靠性。因此，如何设计一套时间序列变量概率预报框架，能获取可靠高精度的径流、风速、太阳辐射强度和负荷概率预报结果是本研究的关键问题，解决该问题可为不确定条件下的风光水互补系统实时调度提供数量依据。

2 风光水时间序列变量概率预报框架

本研究提出一套通用框架可以实现水风光互补系统中时间序列变量的概率预报。框架主要包括深度学习概率预报模型、特征优选和超参数优化等部分。

2.1 深度学习概率预报模型本研究框架采用基于共享权重长短期记忆网络(Shared Weight Long Short-Term Memory Network，SWLSTM)和高斯过程回归的混合模型[36]作为概率预报模型。

2.1.1 共享权重长短期记忆网络 SWLSTM由输入层、隐藏层和输出层组成，其网络结构如图1所示。

图1 共享权重长短期记忆网络结构图

SWLSTM网络在时段t下信息前向传播过程和公式如下：

(1)计算共享门和信息状态

nett=wh·ht-1+wx·xt+b

(1)

st=σ(nett)=σ(wh·ht-1+wx·xt+b)

(2)

at=tanh(nett)=tanh(wh·ht-1+wx·xt+b)

(3)

(2)更新单元状态

Ct=st*Ct-1+(1-st)*at

(4)

(3)计算隐藏层输出

ht=st*tanh(Ct)

(5)

(4)输出预测值

yt=σ(zt)=σ(wy·ht+by)

(6)

式中：xt、st和at分别为当前时段输入层输入、共享门和信息状态；Ct-1和Ct分别为前一时段和当前时段的单元状态；ht-1和ht分别为前一时段和当前时段隐藏层输出；yt为当前时段输出层的输出，也是当前时段的预测值；nett和zt为中间变量，没有具体含义；[wh，wx，b]和[wy，by]分别为隐藏层和输出层权重变量，也是整个神经网络模型需要训练的变量；符号·和符号*分别表示矩阵乘法和矩阵元素间乘法。函数σ(·)和tanh(·)分别是sigmoid和tanh激活函数。

为提升神经网络类模型性能并避免产生过拟合现象，在模型训练过程中增加小批量梯度下降、正则化、衰减学习率和dropout等机制。

2.1.2 高斯过程回归 一系列服从高斯分布的连续随机变量构成了高斯过程。在离散情况下，基于已知样本信息推求未知样本的高斯分布参数即为高斯过程回归，示意图如图2所示。

图2 高斯过程回归示意

采用贝叶斯推理可得验证集预测值y的后验条件分布为：

(7)

(8)

(9)

(10)

2.1.3 SWLSTM-GPR混合模型 其思路是：首先在训练集上完整地训练SWLSTM模型；然后将训练集和验证集输入到训练好的SWLSTM模型中，完成第一次预测；最后将第一次预测结果与观测值重组成新训练集和验证集，调用GPR模型完成第二次预测。

SWLSTM-GPR完整步骤如下：

步骤中xt表示特征输入；y1，t表示第一次预测结果，由SWLSTM模型得到；y2，t表示第二次预测结果，由GPR模型得到；Yt表示观测值；上标ta和te分别代表训练集和验证集标识；Ta和Te分别是训练集和验证集总样本数。

2.2 基于0-1规划思想的特征组合优选在模型预测过程中，所有特征输入共同影响预测结果。一组备选特征如何组合使模型预测精度达到最高是本研究的重点。

假设n个通过特征选择之后的备选特征为[X1，X2，…，Xn]，每个特征均有被选取加入特征组合中和不被选两种状态，但至少要保留一个特征作为输入，因此整个特征组合优化等价于0-1规划问题，搜索空间有2n-1种组合情况。针对某一特征组合，采用预报模型进行训练和预报，可以获取该特征组合对应的预报精度，通过比较不同特征组合的预报精度即可筛选出最优特征组合，如图3所示。

图3 特征组合优化示意

显然，搜索空间大小随维度n增加呈指数增长，当维度n较大时，特征组合优化面临“维数灾”问题，在进行特征组合优化之前可以采用皮尔逊相关系数或者最大信息系数对特征进行初选，减少搜索空间。针对不同维度n，本研究采用不同策略寻优：(1)当07时，总搜索空间大小至少为128，此时采用启发式算法进行搜索。

2.3 基于贝叶斯优化算法的超参数优选预报模型的精度也受模型超参数的影响，以最小化损失函数为例，超参数优化问题可以表示为：

(11)

式中：h*为最优超参数；H为超参数可选范围集合；P为预测模型；h为当前超参数；L(P，h)为预测模型P在超参数h下的损失函数。

本研究采用贝叶斯优化算法(Bayesian Optimization Algorithm，BOA)[37]求解超参数优化问题。相比于其他优化算法，贝叶斯优化算法通过估计整个损失函数概率分布使得新生成的超参数更接近最优结果，从而能够在较少的函数评价次数内获取更优的超参数，其优化过程示意图如图4所示。

图4 贝叶斯优化算法过程示意图

贝叶斯优化算法的完整步骤如下：

步骤1：在超参数可选范围集合H下，随机生成少量超参数子集[hi]；计算预测模型P在每一种超参数hi下的损失值li；构造损失函数分布数据集D=[(hi，li)]；

步骤2：在超参数优化空间数据集D上训练概率回归模型M，通过模型M估计损失函数l的概率分布p(l|h，D)；概率回归模型M不是预测模型P，常用模型M有高斯过程、随机森林和Parzen估计树等模型；

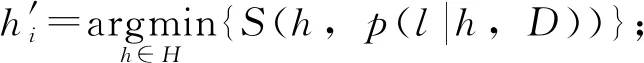
步骤4：计算预测模型P在新生成超参数h′i下的损失值l′i，补充损失函数分布数据集D=D∪(h′i，l′i)；重复步骤2和3，直至迭代完毕；输出最后生成的新超参数作为最优超参数h*。

2.4 预报评价指标本研究提出的时间序列变量预报框架涉及确定性预测和概率预测，因此需要从确定性预测精度、概率预测综合性能和预报可靠性3个方面对预报模型性能进行评价。

(1)确定性预测评价指标。确定性预测指标评价模型预报精度，预测值越接近观测值，则确定性预测精度越高。常用确定性预测精度指标有均方根误差(Root Mean Square Error，RMSE)和确定性系数(Coefficient of Determination，R2)：

(12)

(13)

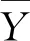
(2)概率预测评价指标。连续分级概率评分(Continuous Ranked Probability Score，CRPS)可评价概率预报综合性能，是平均绝对误差(Mean Absolute Error，MAE)在连续概率分布上的广义形式。其计算方法如下：

(14)

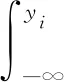
(15)

(16)

式中：预测值yi的概率密度函数和累计分布函数分别为p(yi)和F(yi)；H(yi-Yi)为赫维赛德函数。CRPS越小，概率预报综合性能越好。

(3)可靠性评价指标。可靠性是指预测值和观测值统计的一致性。本研究采用概率积分变换(Probability Integral Transform，PIT)评价预报可靠性。如果验证集上PIT值服从0到1之间的均匀分布，则概率预测结果是可靠的。PIT值通过累计分布函数和观测值计算：

(17)

2.5 时间序列变量概率预报框架风光水互补系统时间序列变量概率预报框架如图5所示，框架中主要包括特征、超参数、预报模型和评价指标4个模块，总体流程如下：(1)特征生成：从时间序列数据中挖掘历史前期特征、周期特征和物理特征，当特征数量较少时，可采用平方、对数等操作对特征进行变换以生成更多特征；(2)特征初选：特征组合优化搜索空间随特征数量呈指数级增长，采用相关系数对生成的特征进行初选，以减少特征组合优化搜索的空间；(3)特征组合：以经过特征初选之后的特征作为备选特征，将特征组合优化问题视作0-1规划问题，采用穷举法、随机搜索或启发式算法求解得到最优特征组合；特征组合优化过程中对每一套特征组合而言，需同时完成超参数优化和模型训练，并采用预测指标对该特征组合进行评价；(4)超参数优化：一套特征组合确定后，采用贝叶斯优化算法对模型超参数进行优选；超参数优化过程中对每一套超参数而言，需完成模型训练并采用预测指标对该组超参数进行评价；(5)预报模型：在最优特征组合和最优超参数下构建SWLSTM-GPR概率预报模型，完成模型训练和预报；特征组合中嵌套超参数优化，超参数优化中嵌套模型训练，三者是同时完成的；(6)评价指标：无论是特征组合，还是超参数优化，亦或是模型训练，都需要采用确定性或概率预报指标进行评价。

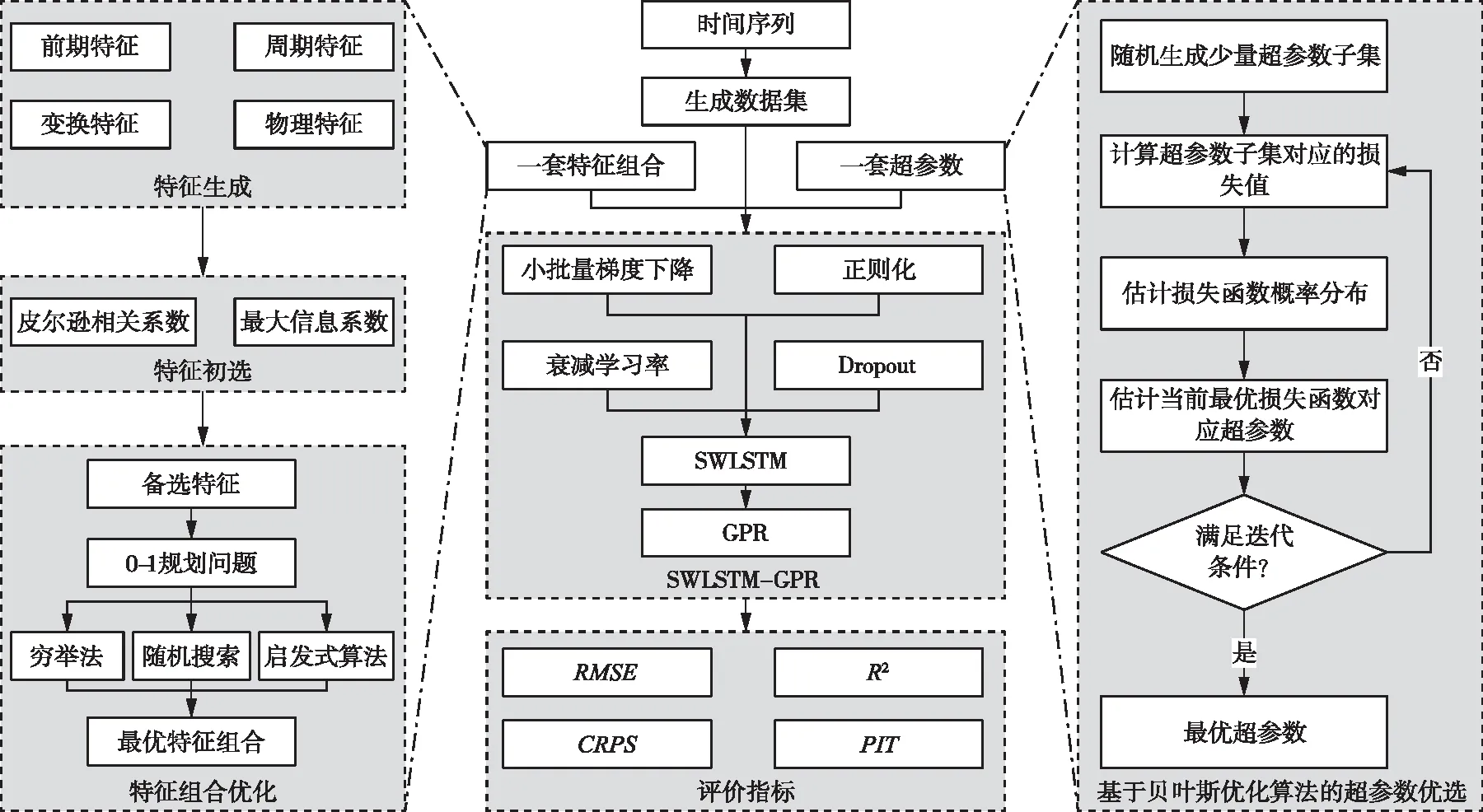
图5 时间序列变量概率预报框架

3 案例研究

3.1 研究对象采用雅砻江流域风光水互补先期试点示范基地作为研究对象。示范基地位于四川省盐源县，青藏高原东南缘，雅砻江中下游西岸，川、滇两省交界处。盐源县经纬度介于北纬27°06′—28°16′、东经100°42′—102°03′之间，全县幅员面积8398.6 km2。幅员内地形地貌以山高、坡陡、谷深、盆地居中为总特征。海拔集中在2500～3000 m之间，最高海拔4393 m，最低海拔1200 m。盐源县风资源密集区主要分布在县城周围海拔较高的山地上，年平均风速在6～8 m/s之间。盐源县年平均太阳辐射量约6100 MJ/m2，属于日照高值区，多年平均日照时数约2570 h。

研究选取雅砻江流域风光水互补示范基地中的径流、风速、太阳辐射强度和负荷4个时间序列变量，分别来自于官地水库、沃底风电场、扎拉山光伏电站和四川省负荷数据集，称为官地径流数据集、W1风速数据集、S1光伏数据集和四川负荷数据集。数据集详细信息如表1和图6所示。

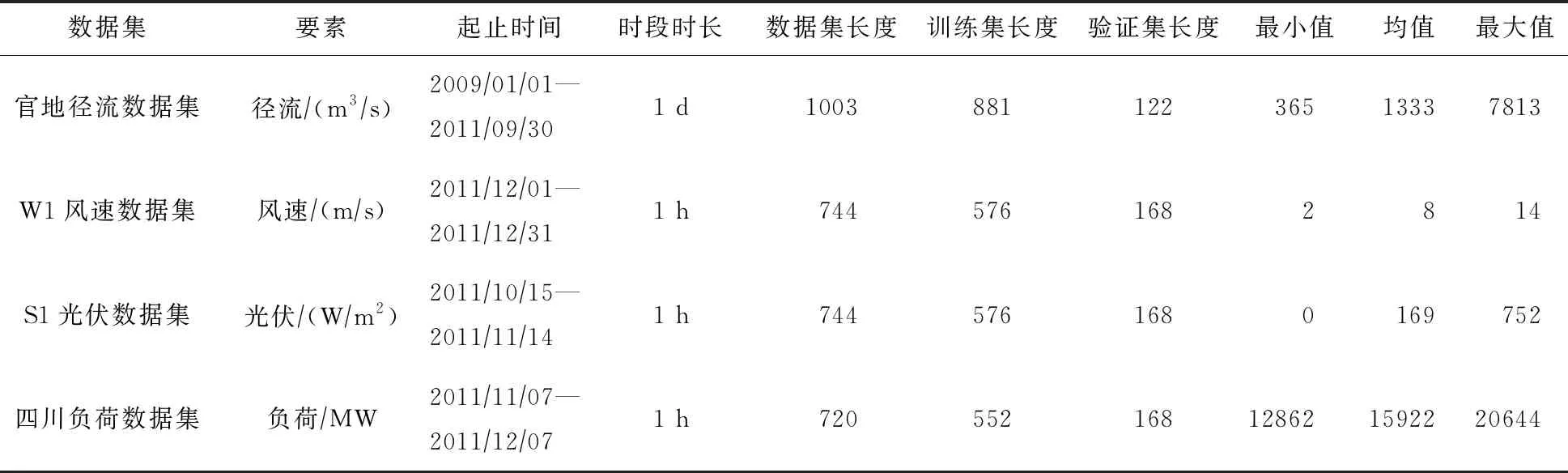
表1 预报实例研究数据集统计信息

图6 预报实例研究数据集

3.2 实验设计为了验证所提出概率预报框架的性能，将SWLSTM与LSTM[25]、GRU(Gate Recurrent Unit)[38]、CNN[27]、ANN[20]、SVR[15]、GPR[34]和XGB(Xgboost)[39]等7个前沿的时间序列变量预报模型在4个数据集上从确定性预报精度、概率预报综合性能和可靠性3个方面进行对比。对于实验中的其他确定性预报模型，均采用本研究框架与GPR结合获取概率预报结果。径流、风速、光伏和负荷4个时间序列变量分别调用本研究提出的框架完成预测，而不是4个变量一次性完成预测。

风光水多能互补系统时间序列变量预报实验目的如下：(1)对4个数据集进行相关性分析，并完成特征初选；(2)对比不同模型特征组合优化结果；(3)以SWLSTM模型为例展示超参数优化结果；(4)在验证集上对比不同模型确定性和概率结果指标；(5)以SWLSTM-GPR模型为例展示4个数据集确定性和概率验证结果；(6)以SWLSTM-GPR模型为例验证概率预报的可靠性。

为了保障对比实验的公平性，实验中所有模型均独立进行特征组合优化和超参数优化，确保每个模型都是在最优条件下进行对比。实验中预报模型参数设置如表2所示，表格中确定的值表示该超参数不需要优化，表格中区间表示该超参数优化的范围。

表2 预报模型参数设置

4 结果分析与讨论

4.1 相关性分析及特征初选综合考虑历史前期特征和周期特征，官地径流数据集和W1风速数据集采用历史前9个时段的值生成特征，S1光伏数据集和四川负荷数据集采用历史前47个时段的值生成特征。采用皮尔逊相关系数绝对值(PCC)和最大信息系数(MIC)探究特征和待预测变量之间的相关性，部分特征相关系数如表3所示，完整相关系数如图7所示，其中F1特征表示前1个时段的历史值，F2特征表示前2个时段的历史值，以此类推。

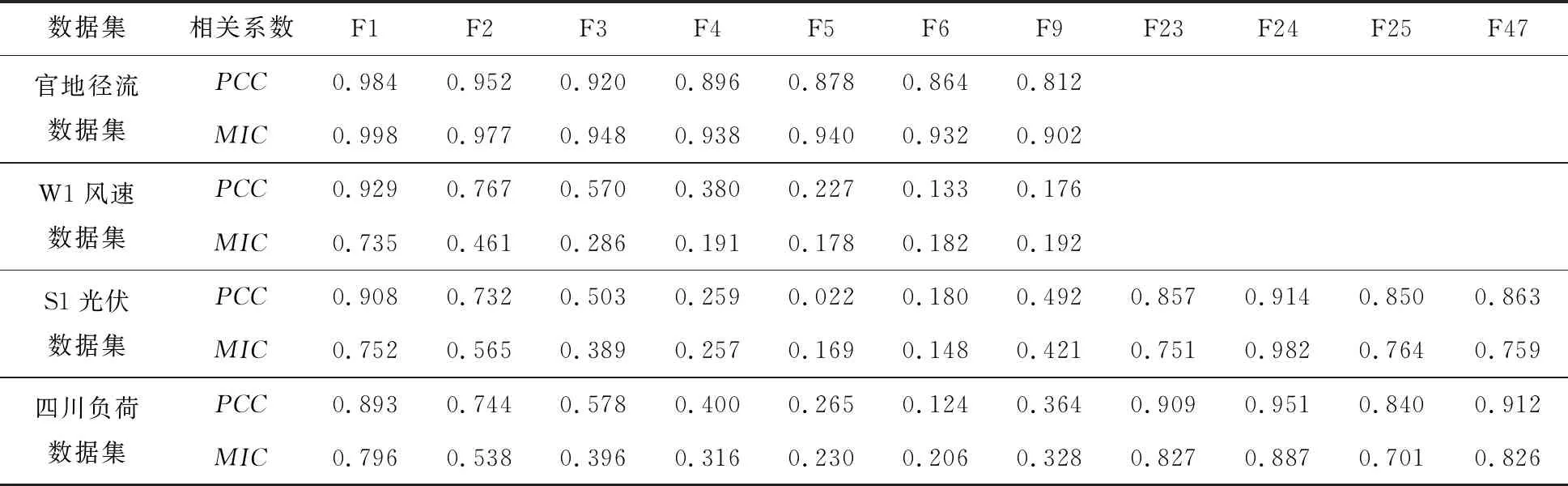
表3 相关系数表

考虑到不同数据集相关系数的差异，针对不同数据集采用不同标准进行特征初选。4个数据集相关系数阈值分别设置为[0.9，0.6，0.8，0.8]。PCC和MIC通过阈值筛选的特征不一定相同，需要考虑取并集特征还是交集特征。综合特征组合优化搜索空间大小以及时间成本，官地径流数据集在PCC和MIC两个指标进行特征初选时取两者交集，其余3个数据集取两者并集。4个数据集特征初选如图7所示。以官地径流数据集和W1风速数据集为例分析如下：

图7 相关性分析及特征初选

(1)图中蓝色和紫色线圈分别代表各特征的PCC绝对值和MIC值，黄色线圈和灰色区间分别代表相关系数阈值和高相关系数区间；对于某一条相关系数线圈而言，落在灰色区间的特征表示通过该相关系数的筛选；绿色虚线表示该特征通过特征初选可作为特征组合优化的备选特征。

(2)在官地径流数据集中，相关系数阈值为0.9，通过PCC筛选后得到的特征为[F1，F2，F3]；通过MIC筛选后得到的特征为[F1，…，F9]；两者取交集，故官地径流数据集通过特征初选之后的特征为[F1，F2，F3]。

(3)在W1风速数据集中，相关系数阈值为0.6，通过PCC和MIC筛选得到的特征均为[F1，F2]；两者取并集，故W1风速数据集通过特征初选之后的特征为[F1，F2]。其余数据集经过特征初选之后的结果分析与之类似，S1光伏数据集和四川负荷数据集通过特征初选之后的特征均为[F1，F23，F24，F25，F47]。

4.2 特征组合优化实验中所有预报模型均完成了特征组合优化，各预报模型在4个数据集上的最优特征组合如表4所示，结果分析如下：

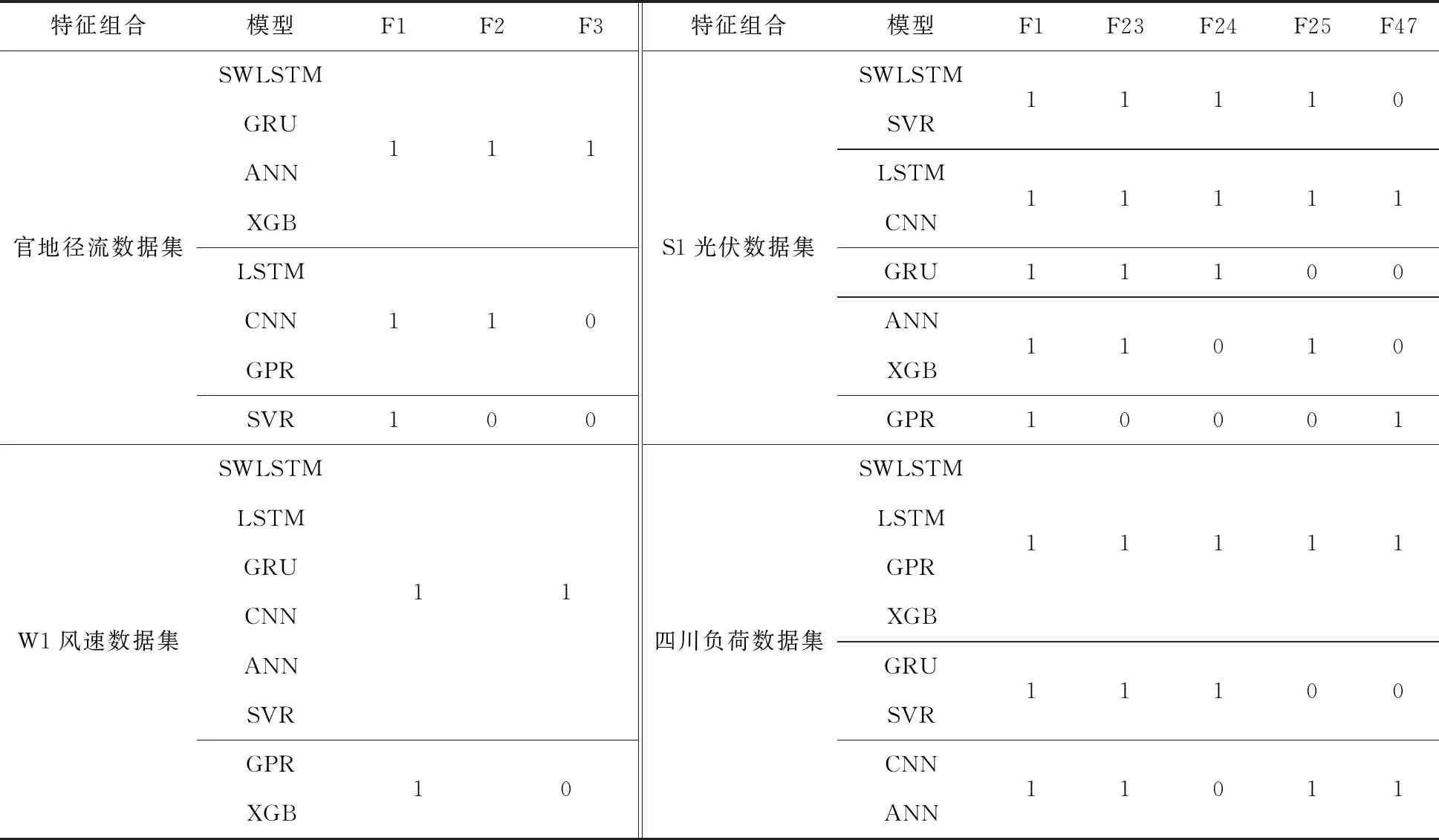
表4 各模型在4个数据集上的最优特征组合

(1)在4个数据集上，没有一个数据集上所有模型的最优特征组合是全部一样的，说明在不计时间成本的情况下对各个模型分别进行特征组合优化有利于提升模型性能。

(2)每个数据集上都存在对多数模型为最优的特征组合，因此在考虑时间成本的情况下，可以采用耗时少模型的最优特征组合近似代替训练费时模型的最优特征组合，例如可以采用GPR、XGB和SVR等模型的最优特征组合代替神经网络类模型的最优特征组合。

(3)对其他模型最优的特征组合，虽然不一定对本模型是最优的，但也是次优或较优的特征组合，再次佐证了特征组合近似替代的思想。

4.3 超参数优化结果实验中所有预报模型均完成了超参数优化，以SWLSTM模型为例，列出其在4个数据集最优特征组合上的前三最优超参数，如表5所示，表格中列出的是优化后超参数的结果，模型其他固定超参数如表2所示。SWLSTM模型待优化超参数分别为小批次大小、dropout比例、隐藏层节点数、隐藏层数和正则化比例，其在4个数据集上的最优结果分别为[64，2.755×10-4，8，2，1.017×10-4]、[8，3.495×10-4，32，2，6.086×10-4]、[8，2.772×10-4，64，1，1.860×10-4]和[32，1.573×10-4，8，2，1.829×10-4]。

SWLSTM模型前三超参数的精度都较高，原因在于一方面特征输入为最优特征组合，大幅度保障了模型精度；另一方面超参数优化范围通过经验设置在常用范围内。在不考虑时间成本的情况下，对预报模型进行超参数优化有利于提升模型性能；在考虑时间成本的情况下，各模型不进行超参数优化时通常需要人工根据经验设置。SWLSTM模型超参数默认设置可参考表2和表5，能保障预报模型具有不错的性能。

表5 SWLSTM模型在4个数据集最优特征组合上的前三最优超参数

4.4 验证结果对比为验证本研究提出预报框架的精度和综合性能，所有模型均采用其在最优特征组合和最优超参数下的结果进行对比。不同模型在4个数据集上的确定性预报和概率预报指标分别如表6和表7所示。从表格中可以分析得出：SWLSTM模型在4个数据集上的确定性预报指标和概率预报指标是8个对比模型中最优的，说明SWLSTM在4个数据集上的确定性预报精度最高、概率预报综合性能是最好的，验证了本研究提出预报框架在时间序列变量预报上的优势。

表6 不同模型在4个数据集上的确定性预报指标

表7 不同模型在4个数据集上概率预报指标

4.5 验证结果展示SWLSTM-GPR预报模型在4个数据集上的验证结果如图8所示，图中蓝色的预测值曲线紧贴红色的真实值曲线，说明确定性预测精度较高；红色的真实值曲线绝大部分均位于灰色的90%预测区间内，对于验证集中未出现在灰色区间中的样本点采用绿色点标出，同时灰色预测区间宽度没有过大，说明预测的区间整体较合适，能为预报、调度决策人员提供较准确的参考信息。本研究提出的预测框架为单步预测框架，图8中验证结果呈现出“序列”的感觉是因为验证集本身有多个时序样本而不是完成的多步预测。

图8 SWLSTM-GPR模型在4个数据集上的预测结果

SWLSTM-GPR模型在4个数据集上典型时段的概率验证结果如图9所示，图中蓝色的概率密度函数(PDF)线都比较饱满，曲线形状没有过高过低、也没有过宽过窄，说明SWLSTM-GPR获取的PDF比较合适。图中有些时段的真实值靠近PDF均值线，有些则离均值线较远，正好说明概率预报结果是可靠的。如果真实值都远离均值线或都位于均值线上，则概率预报结果是不可信的。

图9 SWLSTM-GPR模型在4个数据集上典型时段概率验证结果

4.6 概率预报可靠性本研究采用概率积分变换(PIT)值是否服从均匀分布来验证概率预报的可靠性。SWLSTM-GPR模型的PIT值图如图10所示，图中黑色的PIT值点均匀的分布在对角线附近并覆盖了0到1之间的完整区间，同时所有的PIT值点均位于Kolmogorov 5%置信带内，说明预测的概率密度函数PDF形状没有过高过低或过宽过窄，验证了概率预报的可靠性。

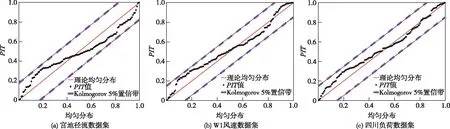
图10 SWLSTM-GPR模型PIT图

5 结论

本研究提出了一种风速、太阳辐射强度、径流和电力负荷等时间序列变量的概率预报框架，该框架融合了深度学习模型、特征组合优化和超参数优化，增强了确定性预报精度和概率预报可靠性。将预报框架运用于雅砻江流域风光水互补先期试点示范基地径流、风速、太阳辐射强度和负荷4个数据集上，实验结果验证了框架的预报性能，可得出以下结论：该预报框架可组合绝大多数预报模型，一方面可通过框架中的高斯过程回归将确定性预报结果扩展为概率预报结果；另一方面框架中特征组合和超参数优化可为预报模型筛选出较优的特征输入和超参数。