输水管道含沙水锤模型及特性研究

汪怡然，俞晓东，石 林，张 健

(河海大学 水利水电学院，江苏 南京 210098)

1 研究背景

近年来，由于水力元件众多、沿线地形地质情况复杂等原因，长距离供水工程的运行事故频发，管路水锤是产生爆管事故的主要原因之一[1]。目前，长距离供水管路水锤问题的研究主要针对单相流或气液两相流(液柱弥合)[2-4]，关于固液两相流的研究较少。而我国主要河流的含沙量较高(例如黄河的平均含沙量高达26.5 kg/m3[5])，含沙水的流动特性又与清水相差甚远。如何求解含沙水锤压力、评估泥沙颗粒参数对高含沙流域长距离供水管路运行安全的影响，成为一个不可忽视的问题。

由于泥沙在液体中受惯性力、重力、阻力的共同作用，其滚动、跳跃、悬移的运动过程难以描述，学者们通常倾向于在宏观上划分固液混合物(本文为含沙水)类型，但基于固相浓度、颗粒直径、沉降速度等参数制定的判定标准尚未统一。本文借鉴费祥俊[6]关于管道断面垂向浓度的Wasp[7]定量指标C/CA(C为管顶下0.08倍管径处的固相体积分数；CA为管路中心处的固相体积分数)为判定标准：定义C/CA>0.8即为均质流(伪一相流)，反之则为非均质流。尽管钱宁和张瑞瑾均认为高含沙水悬移质属于受湍流支持的非牛顿流体，一旦流速下降便会沉降；费祥俊认为以含沙量高低来区分含沙水毫无必要，即便是含沙量900 kg/m3的高含沙水悬移质(C/CA=0.50～0.73)仍属于非均质流[6]。

目前针对含沙水锤的研究较少，但在水力输运领域涉及固液混合物水锤(以下简称浆体水锤)的研究成果较为丰富，这对构建含沙水锤数值计算方法起到了重要的参考作用。韩文亮等[8-11]结合连续性方程、动量方程、管路和固相颗粒的弹性模量与变形量方程，推导了均质流与非均质流的水锤压力波速公式和压力增量公式，采用特征线法计算得到了浆体水锤的混合物波速和瞬态压力，计算结果与实验数据吻合程度较高。这一方法得到了国内外专家学者的广泛运用[12-14]，成为最主流的浆体水锤数值计算方法。此外，周云龙等[15]基于CFD(计算流体力学)技术动网格方法探究阀门关闭时间对浆体水锤压力增量的影响规律，结果显示最大压力增量随着关阀时间的延长而减小，这与清水间接水锤的规律一致。李艳等[16]基于AMESim软件探究粗颗粒均质流垂直管道浆体水锤特性，得出了随着管道长度的增加、管道直径的增加、颗粒浓度的减小，垂直管路浆体水锤最大压力增量减少的结论。尽管浆体水锤与含沙水锤的原理一致，但含沙水(多为低浓度非均质流)与浆体(多为高浓度均质流)的流动特性存在明显差异；且已有研究表明，非均质流的压力波速高于均质流，且随着固相浓度的增加差值逐渐增大[8]。因此，含沙水锤的数学描述不能直接套用浆体水锤的计算模型，应当结合含沙水的管道流动特性与非均质流水锤压力波速公式进行研究。

目前，针对管路的清水水锤计算和浆体水锤计算大多采用特征线法。本文基于费祥俊阻力模型和浆体水锤波速公式，推导了非均质流含沙水锤特征线方程；同样采用特征线法求解了RPV系统的关阀水锤压力，探究了含沙量、颗粒直径与初始流速对含沙水锤压力的影响，总结了一般性规律。研究结论可为含沙流域长距离供水管路水锤计算与防护设计提供参考，指导工程实践。

2 含沙水流动特性与含沙水锤求解

2.1 含沙水流动特性相较于含沙水流型、流态及速度分布等流动特性，管路水头损失对于水锤过程的影响较大。在计算含沙水管路的水头损失之前，仍需对本文界定的含沙水类型做出一定的假设：

(1)假设不同固相浓度的含沙水均为非均质流，忽略颗粒沉积对管道沿程阻力系数的影响。

(2)假设不同固相浓度的含沙水均为牛顿流体，忽略高含沙水悬移质对流动特性的影响。

(3)假设含沙量S、颗粒平均密度ρs、颗粒平均直径ds可以表征含沙水的固相浓度、密度和颗粒直径，忽略颗粒形状(假设为球形颗粒)、颗粒级配、固相浓度及密度分布对含沙水流动特性的影响。

目前，基于经验或半经验理论，专家学者们提出了诸多的管路阻力模型和水头损失计算公式[17]，在此不做赘述。本文选用兼顾悬移质和推移质作用的费祥俊阻力模型[18]，其中非均质流含沙水管路水头损失hm的计算式为：

(1)

式中：h0为清水的水头损失；hs为颗粒运动引起(以沉降为主)的附加水头损失；在清水项h0中，f0为清水沿程阻力系数(在工程中常用管道糙率n表示)；g为重力加速度；D为管径；v为含沙水流速；ρL为液相(水)的密度；ρm为含沙水平均密度；α为考虑悬移质对紊流抑制作用的阻力影响系数，可以基于下述表达式计算[19]：

α=1-0.4lgμr+0.2(lgμr)2

(2)

式中μr为混合物黏度与清水黏度的比值，可根据Einstein稀悬液黏度公式μr=1+2.5S/ρs计算得出。

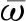
(3)

由于阻力系数本身不易测得，前人基于大量的试验数据，构建了阻力系数CD和颗粒雷诺数Red的关系图，其中颗粒雷诺数Red关于液相黏度μL的计算式为：

(4)

(5)

(6)

这样，联立式(1)(2)(6)即可计算得到长距离供水管路非均质含沙水流的水头损失。

2.2 含沙水锤求解方法关于清水水锤的特征线法与管路水力元件及边界条件的数学描述在文献[4]中有详细描述，本文不再赘述。若想采用特征线法求解含沙水锤方程，需做出以下假设：

(1)假设管路截面面积保持不变，忽略泥沙淤积对于管路截面形状的影响；

(2)假设水锤过程中压力波速保持不变，管路截面压力不受固相颗粒分布的影响；

(3)忽略泥沙对泵、阀等水力元件性能的影响，假设管路水力元件的数学描述与文献[4]一致；

(4)忽略瞬态摩阻变化对含沙水锤过程的影响，管路糙率按稳态流动的水力损失计算。

基于上述假设，借鉴韩文亮的非均质流浆体水锤压力波速公式[8]计算含沙水锤压力波速am的数值，其表达式如下：

(7)

式中：Ew为清水的弹性系数；Es为固相颗粒的弹性模量；e为管路壁厚；E为管路材料的弹性模量。结合式(1)、式(7)与文献[4]中简化后的用于清水水锤计算的运动方程和连续性方程，可以得出含沙水锤的运动方程L1和连续方程L2表达式如下：

(8)

(9)

由于非恒定摩阻在清水水锤过程中对水锤压力第一个周期的影响较小，本文忽略瞬态摩阻变化对含沙水锤过程的影响，定义当量摩阻fm表征非均质流含沙水管路稳态流动的水头损失：

(10)

式中当量摩阻fm可由稳态流动初始条件的f0、v0计算得出。将当量摩阻fm代入方程(8)中得到改进后的含沙水锤的运动方程L1如下：

(11)

通过引入未知因子λ关联方程(11)与方程(9)构建线性组合公式L=L1+λL2=0，求解得到λ的两组特征根代入线性组合公式中得到两组方程分别用C+和C-表示，其具体表达式如下：

(12)

(13)

引入管路截面面积A与含沙水流量Q表征混合物流速v，对特征线方程进行积分，令v=Q/A，B=am/gA，R=fmΔx/2gDA2得到差分形式的代数方程如下：

C+：HP=HA-B(QP-QA)-RQA|QA|=0

(14)

C-：HP=HB+B(QP-QB)+RQB|QB|=0

(15)

在方程(14)和方程(15)的基础上引入边界条件与水力元件代数方程，即可求解得到特定时间位置参数P点的压力HPi与流量QPi的数值解。

3 理论分析

3.1 清水模型验证现以Bergant等[22]RPV系统(水箱-管路-阀门)的清水关阀水锤实验数据为参考，采用前节所述含沙水锤数值计算特征线方法进行关阀瞬变流分析。该实验包含高为32 m的上游水箱，通过长度为37.2 m、直径为0.022 m的管道连接至末段阀门，管道清水条件下的糙率n为0.037。在初始流速v0为0.3 m/s、关阀时间为0.009 s的实验条件下，测量得到了管道末端与中点的清水水锤瞬态压力数据。为了更好地对比清水水锤与含沙水锤的数值计算结果，针对ρm=2650 kg/m3的泥沙颗粒，在颗粒直径ds=0.01～0.5 mm、含沙量S=1～100 kg/m3的范围内，选取三组不同参数介质(其中一组为清水，即含沙水颗粒参数设定为S=0 kg/m3，ds=0 mm)进行对比分析如图1所示。此外，由于含沙水与清水的密度不同，本文将含沙水压力水头Hm统一换算至清水压力水头Hw，其表达式如下：

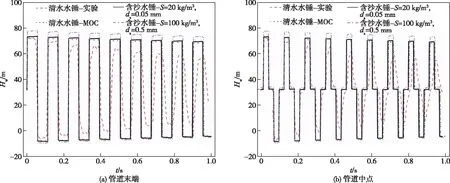
图1 含沙水锤数值计算瞬态压力与清水水锤实验压力对比

(16)

从图中可以看出，清水水锤压力的瞬态数值计算结果与Bergant实验数据在水锤压力波的第一个周期内吻合程度较好，其最大压力值为72.32 m与实验值偏差小于0.5%；而第一个周期后仿真数据与实验结果的偏差较大，这种压力波衰减速率和波速变化的不同主要是受到实验误差与瞬态摩阻效应影响。对于另外两组泥沙而言，S=20 kg/m3，ds=0.05 mm时计算得到的最大瞬态压力为73.45 m，较清水水锤高出1.55%；而S=100 kg/m3，ds=0.5 mm时最大压力值为77.91 m，较清水高出7.71%。对于最小压力值而言，含沙水锤与清水水锤数值计算结果的偏差量小于1.62 m，较最大压力而言偏差较小。无论是管道末端还是中点的含沙水锤压力波动规律与清水仿真一致，其波速存在一定的偏差但差别较小。可以看出，低含沙量、低颗粒直径的含沙水锤压力与清水水锤更为接近，而与高含沙量、高颗粒直径的偏差较大。这一方面论证了含沙水锤数值计算结果随颗粒浓度和直径变化趋势的合理性，另一方面说明了一定规模的颗粒存在对于含沙管路水锤压力产生一定的影响，需要进一步具体地分析不同的颗粒参数对含沙水锤过程压力波动的影响。

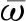
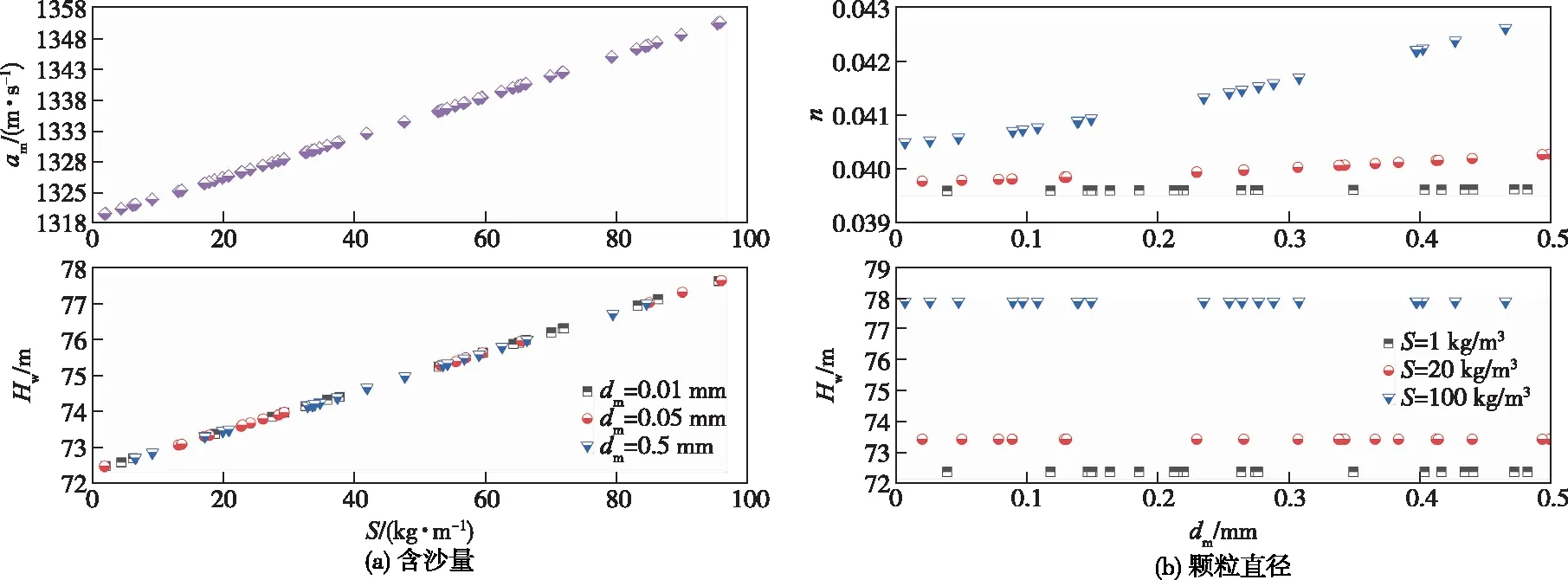
图2 不同颗粒参数与波速、糙率、最大压力关系对比

3.3 流动参数分析计算得到不同初始流速条件下相同颗粒参数(S=20 kg/m3，ds=0.05 mm)的瞬态压力变化如图3所示。结果表明不同流速条件下的压力增量不同而波速相同，这与文献[4]中清水水锤的规律一致；此外，不同流速条件下的压力波衰减过程不同，需要进一步分析相关因素糙率的变化规律。图4的计算结果表明，含沙水水锤过程的压力增量与初始流速线性相关，这与清水水锤Joukovsky方程[4]描述的规律是一致的。然而，本文给定管路条件的清水波速为1319 m/s，给定颗粒参数下的含沙水锤波速为1325.5 m/s，其最大压力计算结果与压力增量变化率存在明显偏差。进一步分析不同初始流速条件下的糙率变化可以看出，当流速小于0.05 m/s时糙率与流速呈现出明显负相关；而当流速大于0.05 m/s时逐渐趋于0.0396不变，这与给定的管道清水条件糙率0.037增大约7%。

图3 不同初始流速瞬态压力波动对比

图4 不同管道流速最大压力与糙率对比

综上所述可以得出含沙量、颗粒直径与初始流速共同影响非均质流含沙水稳态流动的管路糙率，而初始流速与含沙量同时也会对水锤过程的压力增量产生影响，且不同颗粒参数与流动参数对水锤过程压力波动影响的程度和相关性不一。

4 结论

本文基于含沙水费祥俊阻力模型、韩文亮非均质流浆体水锤方程和特征线方法，定义了恒定当量摩阻，构建了含沙水锤的特征线方程，建立了RPV系统关阀的数值计算模型，并结合清水实验验证。结果表明：不同颗粒参数含沙水锤计算结果最大压力差值明显，而最小压力的差别相对较小；含沙量与颗粒直径越小，含沙水锤瞬态压力计算结果与清水实验数据越接近；随着含沙量的增加，含沙水锤的压力增量增大，含沙量100 kg/m3时的最大压力较清水水锤高出7.71%，但颗粒直径对压力增量的影响较小；当量摩阻换算得到的管路糙率与含沙量和颗粒直径呈正相关，与初始流速呈负相关，给定颗粒参数范围内糙率变化超过4.7%。

含沙水锤过程中颗粒对摩阻影响的作用机理十分复杂，本文采用恒定流当量摩阻代换，存在一定的误差。此外，对于长期运行的供水管路而言，颗粒沉积甚至堵塞现象十分严重，非均质流固液混合物的水锤压力波速公式往往不能适用，还需要研究颗粒沉积对波速的影响。上述两方面问题将结合模型实验开展进一步研究。