堤坝混凝土防渗墙渗透溶蚀演化规律研究

甘 磊，陈官运，沈振中，徐力群

(河海大学 水利水电学院，江苏 南京 210098)

1 研究背景

我国堤防工程大多是傍河而建，表现出堤基条件差，堤身质量差，堤后坑塘多，覆盖层薄弱等特点。黄河下游河道是举世闻名的“善淤、善决、善徙”的地上悬河，其右岸临黄堤长624.248 km，左岸临黄堤长746.979 km，部分堤段采用混凝土防渗墙进行基础防渗，这些混凝土防渗墙常年受渗流作用，因环境水作用，其物理、化学性能改变[1]，导致固相钙分解析出，孔隙率增大，强度降低，即发生渗透溶蚀现象。

渗透溶蚀是混凝土结构主要病害之一[2]，我国许多混凝土坝在运行多年后逐渐显现裂缝、渗透溶蚀等老化病害，其中渗漏及其引起的坝体混凝土溶出性侵蚀较为普遍[3]，如运行70多年的丰满混凝土重力坝，坝体混凝土已遭到了明显溶蚀破坏。对坝体钻孔检查发现，坝体内部混凝土表现出极强的空间变异性，混凝土抗压强度一般在15 MPa以上，但局部无法取芯，实际强度低于10 MPa。渗漏部位的坝体混凝土强度下降可达 20%，局部区域则达 70%，甚至完全失去强度成为疏松体[4]。罗湾混凝土重力坝，运行9年以后，廊道内部分排水孔口 CaCO3晶体呈瀑布状，现场检测发现，溶蚀部位混凝土后期强度不仅未增长，反而明显下降，挡水运行10年后仅为设计值的83%[5]。

目前，关于溶蚀现象的研究，多为不考虑渗流作用的接触溶蚀，钙离子析出的驱动力是溶液间的浓度梯度[6]。然而，对于堤坝混凝土防渗墙而言，渗流作用对溶蚀进程的影响不容忽视。渗流作用下渗透溶蚀钙离子析出的驱动力不仅是浓度梯度，还有水力梯度。在水力梯度作用下，孔隙溶液的运移作用加快了固相钙的分解速率和钙离子析出速率，加速了溶蚀进程[7]。同时，渗流作用下混凝土产生渗透溶蚀现象，将导致材料孔隙率增加，从而引起渗透系数和扩散系数增大，进而改变结构整体的渗流场，渗流场的改变又反作用于溶蚀场，加速溶蚀进程[8-10]。

在水泥基材料渗透溶蚀数值模型研究方面，Nakarai等[9]将硬化水泥基体中钙离子的析出模拟为钙的固-液两相平衡的过程，从热力学角度推导了钙离子运移过程。Yokozeki等[10]分析了温度对钙离子浸出过程的影响，建立了水化产物溶解度平衡模型，结合溶解度模型和对流扩散模型模拟了混凝土中钙离子的析出。Ulm等[11]提出了基于固相钙分解反应速率计算方法的化学-孔隙-塑性理论。Gawin等[12]在Ulm等理论基础上，研制了去离子水中的水-力-化学溶蚀模型。Huo等[13]建立了反映渗流、化学及细观结构等特征的多场耦合模型，研究渗透溶蚀对帷幕孔隙率和防渗性能的影响。彭鹏等[14]依据渗流水力学及水文地球化学基本理论，建立了反映帷幕体防渗时效多场耦合作用模型。现有水泥基材料渗透溶蚀分析模型仍存在一些问题，已有研究有的将渗透系数定义为常数，忽略溶蚀作用所导致的渗透系数演变；有的采用经验模型，未考虑孔隙率、孔隙结构改变对渗透系数的影响，也未对材料固相钙含量、渗透系数等参数进行分析，存在一定局限[15-16]。目前，堤坝防渗墙渗透溶蚀演化规律的相关研究成果尚少，但渗透作用会加速坝基防渗墙的溶蚀进程，缩短坝基防渗墙使用寿命。

本文针对混凝土防渗墙渗透溶蚀问题，考虑混凝土防渗墙渗流-溶蚀耦合效应，提出基于孔隙率变化的渗透溶蚀微分控制方程。结合某土工膜堤坝工程，建立该堤坝多物理场渗透溶蚀数值模型，研究渗流作用下混凝土防渗墙渗透溶蚀演化规律，研究成果可为堤坝工程长效服役性能评估提供理论依据。

2 混凝土渗流-溶蚀耦合分析模型

2.1 钙离子质量守恒定律水泥水化物的孔隙溶液中存在一些离子，当孔隙内外浓度存在差异时，通过扩散作用而使浓度保持平衡。通常，多孔介质中的扩散现象通过表观扩散系数计算，研究混凝土内离子扩散系数时，假定骨料不会发生扩散现象，考虑骨料对离子传输路径的影响(传输路径曲折度)，如图1所示。

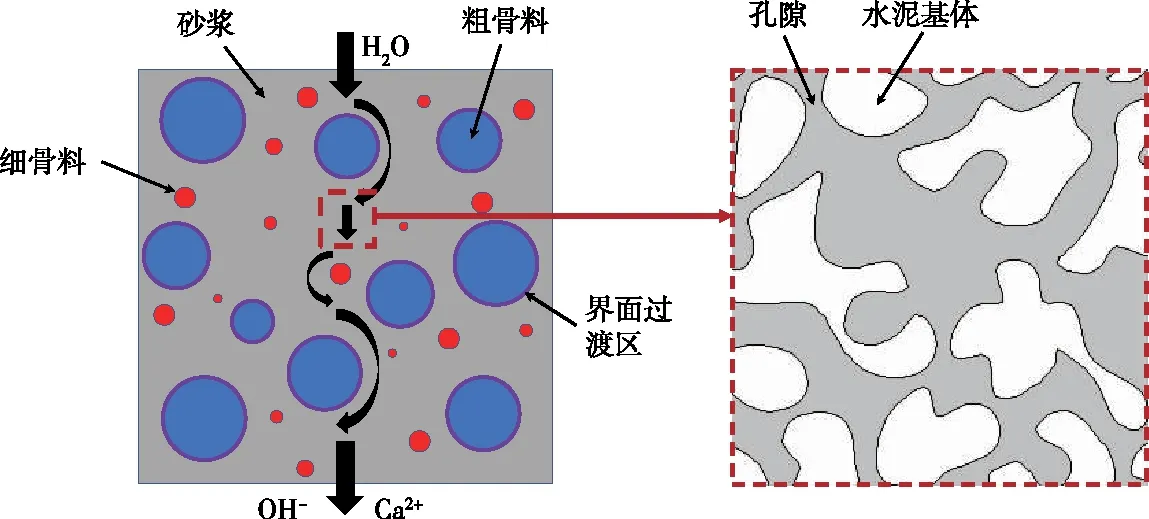
图1 混凝土细观孔隙内的离子传输模型

钙离子在水泥基体孔隙溶液中的质量守恒定律如式(1)，涉及孔隙溶液中钙离子总质量和浆体中固相钙的总质量[9-10，12]。

(1)

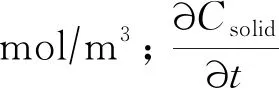
考虑扩散-对流情况下钙离子在多孔介质中的传输通量为[17-18]

(2)

式中：Deff为基体内考虑对流及孔隙曲折度的钙离子有效扩散系数，m2/s；u为达西流速，uT=[ux，uy]，m/s。

2.2 孔隙率变化模型硬化的水泥基体中的孔隙可大致分为滞留空气、夹带空气、毛细孔和凝胶孔，溶蚀过程中的孔隙率可表示为[19-22]：

θ=Pvol(θgel+θcap)+θleach

(3)

其中

(4)

(5)

(6)

式中：Pvol为混凝土中水泥基体的体积分数，本文取0.26[10]；θgel为凝胶孔隙率；θcap为毛细孔隙率；θleach为溶蚀过程产生的孔隙率增量；hα为水泥水化程度；w/c为水灰比，本文取0.6[10]；MCH为氢氧化钙的摩尔质量，g/mol；ρCH为氢氧化钙的密度，kg/m3；Cs0为基体中初始固相钙含量，mol/m3；Cs为溶蚀过程中基体中固相钙含量，mol/m3。

混凝土防渗墙内可溶解固相钙主要由氢氧化钙和水化硅酸钙组成。在环境水侵蚀作用下，混凝土内的氢氧化钙和水化硅酸钙依次溶解，首先氢氧化钙开始溶解，当氢氧化钙全部溶解后，水化硅酸钙开始溶解。本文仅考虑氢氧化钙的溶解[13，23]，随着氢氧化钙的不断溶解，防渗墙的孔隙率不断增大，其增长速率为

(7)

式中：RCH为氢氧化钙的溶解速率，mol/(m3·s)。氢氧化钙的溶解速率与溶液中钙离子浓度有如下关系[13，23]：

(8)

式中：A为化学反应动力学系数；n为动力学指数；C(Ca2+)为溶液中钙离子浓度，mol/m3；C(OH-)为溶液中氢氧根离子浓度，mol/m3；Ksp为氢氧化钙的溶度积常数。

2.3 扩散系数变化扩散作用下，以孔隙溶液与完全不受基质影响的稀溶液作为扩散介质，其扩散系数有着较大差异。如果认为微孔是一组大而均匀的孔隙，且钙离子在水泥水化物及骨料中不会发生扩散，则由于曲折度的影响，钙离子在微孔内沿实际路径的迁移距离大于基质长度，因此，表观扩散系数较低。同时，当孔隙数量增加时，扩散系数也随之增大。因此，取钙离子在水溶液中的基本扩散系数D0，根据孔隙率和基质曲折度的变化，孔隙溶液的有效扩散系数表示为：

(9)

式中：Gvol为混凝土中粗骨料的体积分数，本文取0.414[10]；Svol为混凝土中细骨料的体积分数，本文取0.326[10]；ξ和ζ为骨料修正系数，本文分别取1.5和0.86[24]；Pvol为混凝土中水泥基体的体积分数；f(θ-θgel)为反映微孔曲折度的换算系数[10]，计算如下式所示：

f(θ-θgel)=0.001+0.07(θ-θgel)2+1.8H(θ-θgel-0.18)(θ-θgel-0.18)2

(10)

式中H(x)为Heaviside函数。当x>0时，H(x)=1；当x≤0时，H(x)=0。

考虑对流及孔隙曲折度的钙离子有效扩散系数可表示为[15]：

Deff=α·u+Ds

(11)

式中α为弥散度，m。

2.4 渗流-溶蚀耦合分析方程孔隙溶液中溶质迁移的对流速率在无流动水中为零，当环境水存在水力梯度时，根据渗流微分方程计算对流速率。根据达西定律建立的渗流微分方程为：

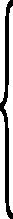
(12)

式中：ρ为水的密度，kg/m3；Qm为源汇项，kg/(m3·s)；p为孔隙水压力，Pa；g为重力加速度，m/s2；k为渗透系数，m/s。水泥基材料的渗透系数通常为孔隙率的函数，根据Kozeny-Carman(K-C)方程可得渗透系数的演化方程为[25]：

(13)

式中：k0为初始渗透系数，m/s；θ0为初始孔隙率，本文取混凝土水化完全时(hα=1)的孔隙率作为初始孔隙率。

图2为渗流-溶蚀耦合求解过程流程图，通过式(12)计算出孔隙溶液对流速率，进而影响式(2)中钙离子在多孔介质中的传输通量，改变钙离子扩散系数，进而实现钙离子的迁移扩散，混凝土孔隙率增加，渗透系数变大，从而对渗流场产生影响，实现渗透溶蚀耦合过程。基于钙离子在水泥基体孔隙溶液中的质量守恒定律公式(1)和渗流微分方程式(12)，建立混凝土防渗墙渗透溶蚀耦合非线性偏微分方程组，采用有限元法进行数值求解，运用COMSOL Multiphysics软件中的达西定律模块及溶质运移模块进行渗流场和溶质运移场的耦合分析。

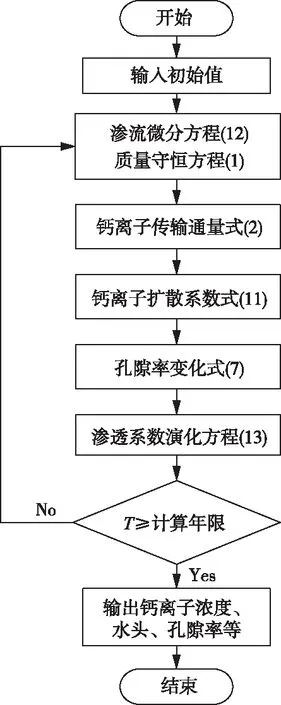
图2 渗流-溶蚀耦合求解过程流程图

3 试验论证

本文采用文献[19]混凝土试件溶蚀算例进行模型验证，试件横断面尺寸为100 mm×100 mm，模拟其全部浸泡在软水中的溶蚀情况，研究其溶蚀深度演化规律，混凝土配合比见表1，有限元网格模型如图3所示。

表1 混凝土配合比

图3 混凝土试件有限元网格模型

图4为混凝土试件浸泡360 d后的钙离子浓度分布图。从图4可看出，钙溶蚀过程是一个由表及里的过程，符合试验规律。当孔隙溶液中钙离子浓度为19.1 mol/m3时，氢氧化钙晶体完全溶解，故以浓度19.1 mol/m3等值线到混凝土表面的垂直距离作为钙溶蚀深度。不同溶蚀时间下钙离子随溶蚀深度(h)变化规律如图5所示，图中曲线与虚线交点的横坐标代表混凝土溶蚀深度。图6为溶蚀深度随溶蚀时间的变化曲线。由图6可知，溶蚀深度随时间增大而增大，溶蚀60、120、180、240和320 d后混凝土试件溶蚀深度分别为3.4、4.6、5.4、6.2和7.2 mm，混凝土溶蚀深度与时间的平方根呈较好线性关系，与文献[19]结果较为吻合。

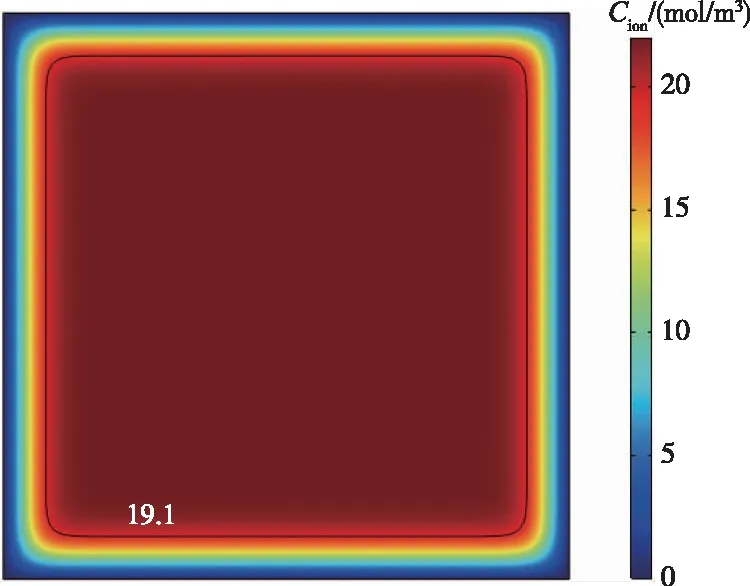
图4 试件浸泡360 d钙离子浓度分布

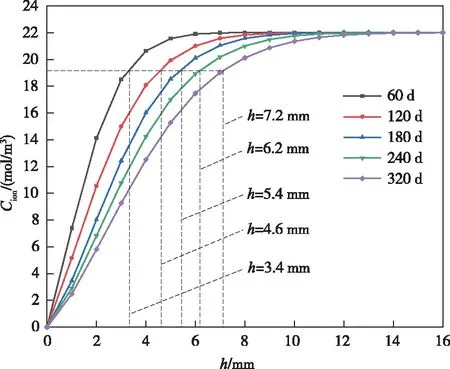
图5 不同溶蚀时间下钙离子浓度随溶蚀深度的变化曲线

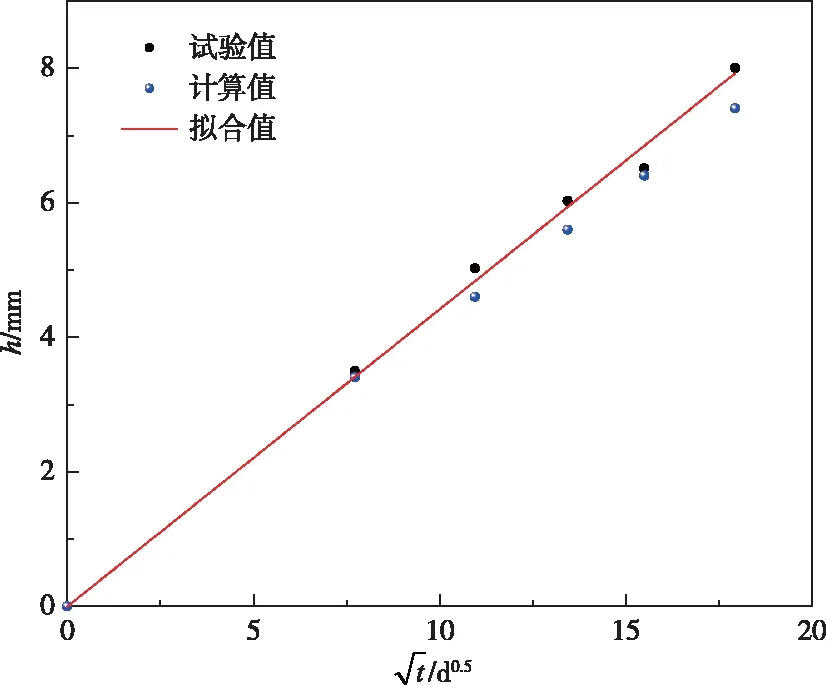
图6 溶蚀深度与侵蚀时间的关系曲线

4 应用实例

4.1 计算模型和参数某堤坝位于黄河干流上，为复合土工膜砂砾石坝，坝顶高程1883.50 m，最大坝高23.50 m，正常蓄水位1880.50 m，上游坝坡布置1道复合土工膜防渗，并与上游围堰中的混凝土防渗墙相接，混凝土防渗墙厚0.6 m，防渗墙设计顶高程为1870.00 m，防渗墙底部深入微透水的弱风化岩体中。

采用COMSOL Multiphysics软件建立该堤坝典型断面有限元计算模型，考虑坝体主要结构和地层，计算模型如图7所示。上游库水中钙离子浓度取1.0 mol/m3[15]，上游水头边界取正常蓄水位1880.50 m以下坝体上游面与河床覆盖层顶部，下游水头边界取正常尾水位1862.31 m以下坝体下游面与河床覆盖层顶部，正常尾水位以上坝体下游面设置出逸边界，坝基上游边界、下游边界和底边界设置为不透水边界。计算区域材料渗透参数由地勘部门提供；防渗墙初始孔隙率取为0.12，运行过程中由式(3)计算所得，其它非水泥基材料的孔隙率按工程经验选取，运行过程中不发生变化；考虑到骨料及孔隙对钙离子传输路径的影响，防渗墙有效扩散系数D0由式(11)获得；化学反应动力学参数参照文献[15]和水库年平均温度20 ℃综合确定，堤坝计算模型渗透溶蚀参数如表2所示。

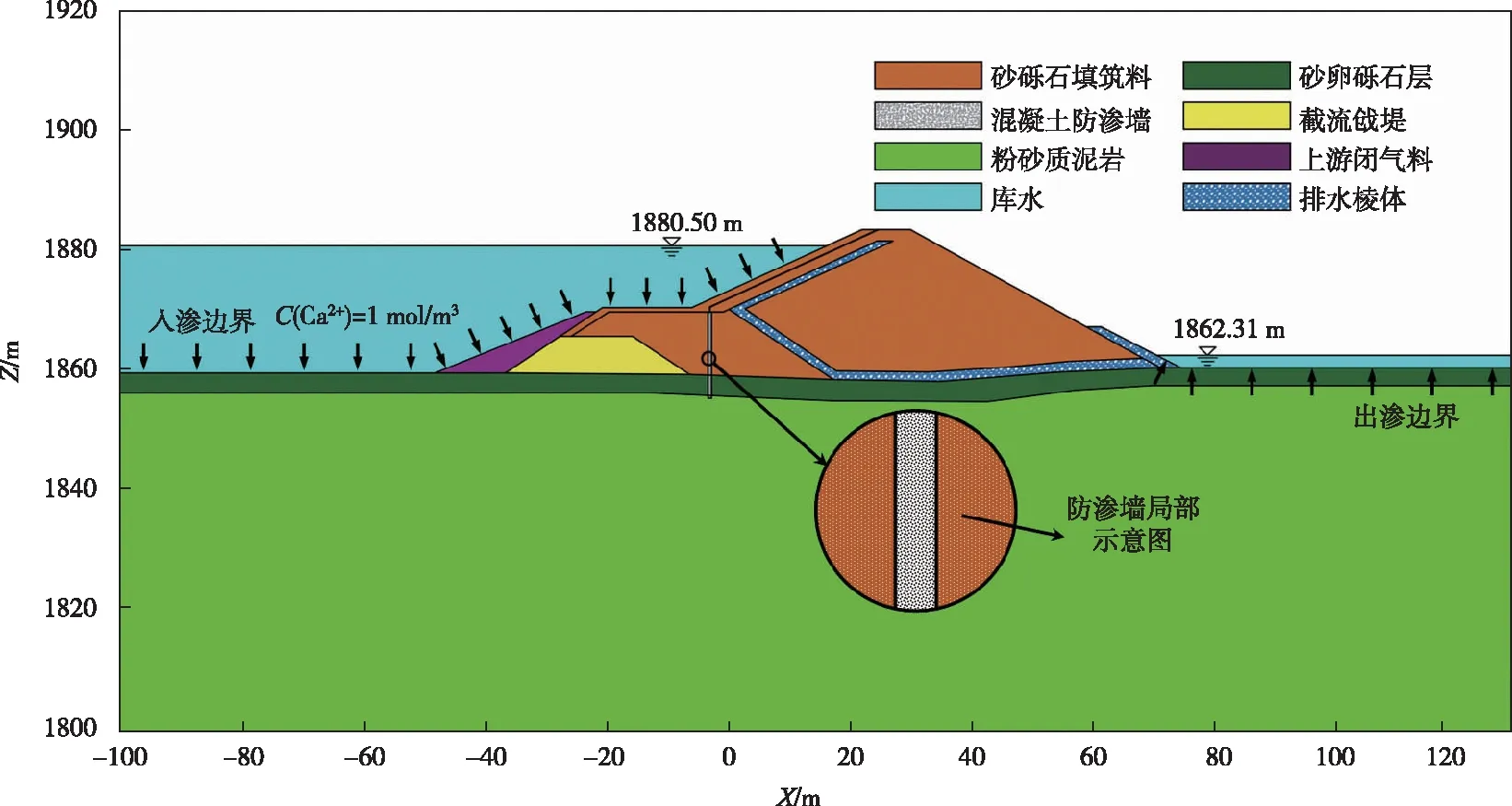
图7 计算模型示意

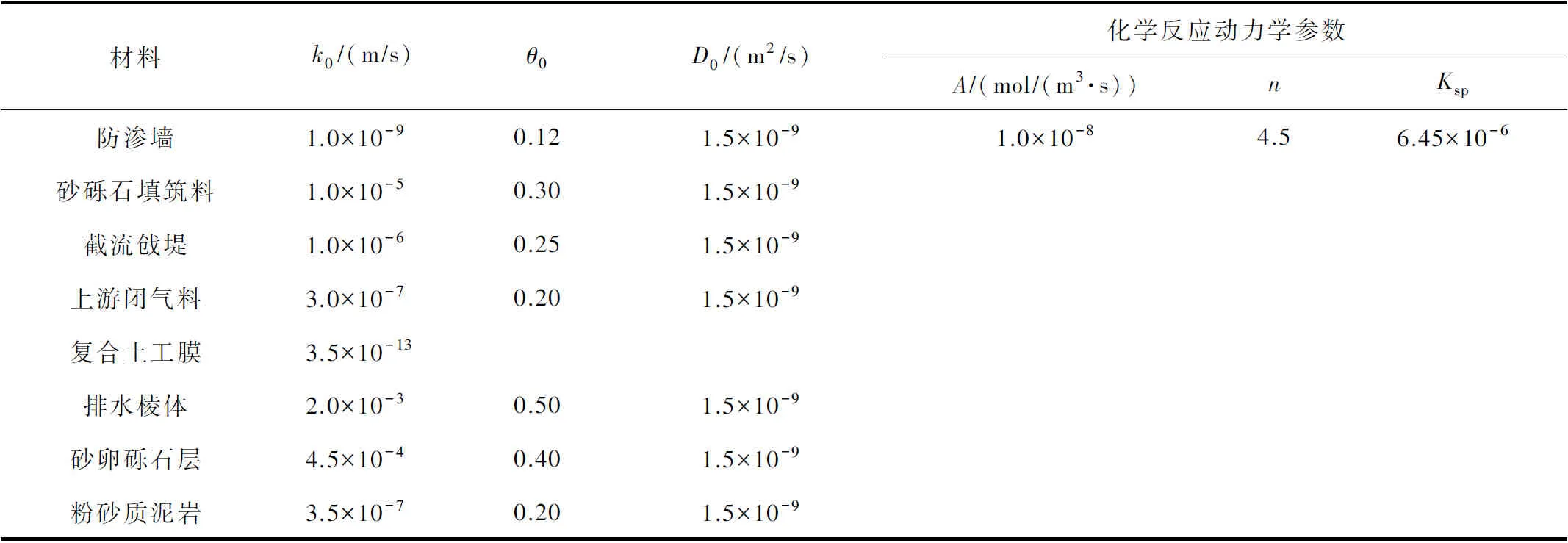
表2 计算模型渗透溶蚀参数

4.2 结果与讨论

(1)钙离子分布。图8为不同服役年份下混凝土防渗墙中钙离子浓度分布图。由图8可知，防渗墙顶部和底部钙离子浓度值较中部低，运行20 a时，防渗墙内部钙离子浓度最大值为5.239 mol/m3，运行100 a后，钙离子浓度最大值仅为2.485 mol/m3，随着运行时间增加，防渗墙中钙离子整体浓度不断降低，年平均变化速率约为0.03 mol/(m3·a)。

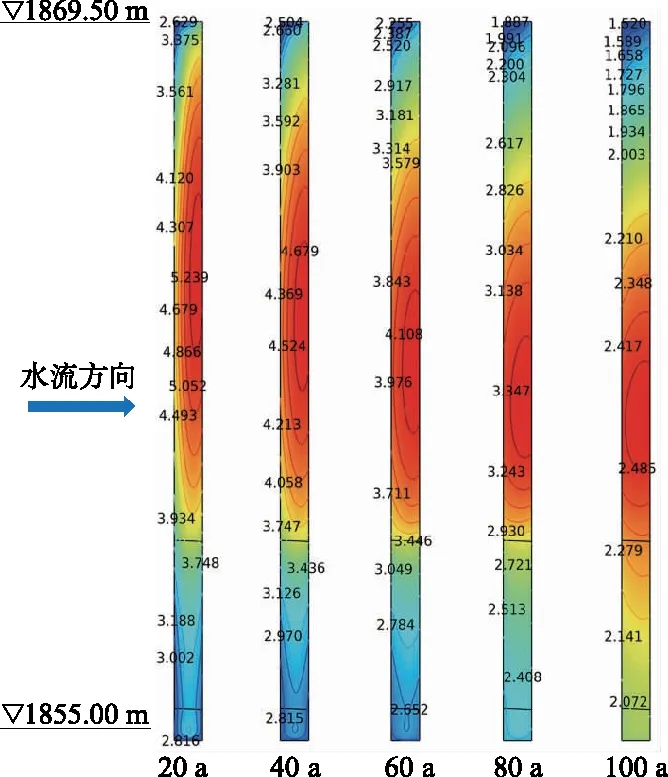
图8 防渗墙钙离子浓度分布(单位：mol/m3)

防渗墙3个典型位置，点A(-1.9，1869.0)、点B(-1.9，1863.0)、点C(-1.9，1856.0)的钙离子浓度变化如图9所示。由图9可知，3个典型位置的钙离子浓度随服役年限增长均不断降低，与文献[15]中所得变化趋势和数量级较为一致。钙离子浓度是表征防渗墙溶蚀量的指标，钙离子浓度低说明对流迁移速率大，防渗墙溶蚀反应强，溶蚀量高。

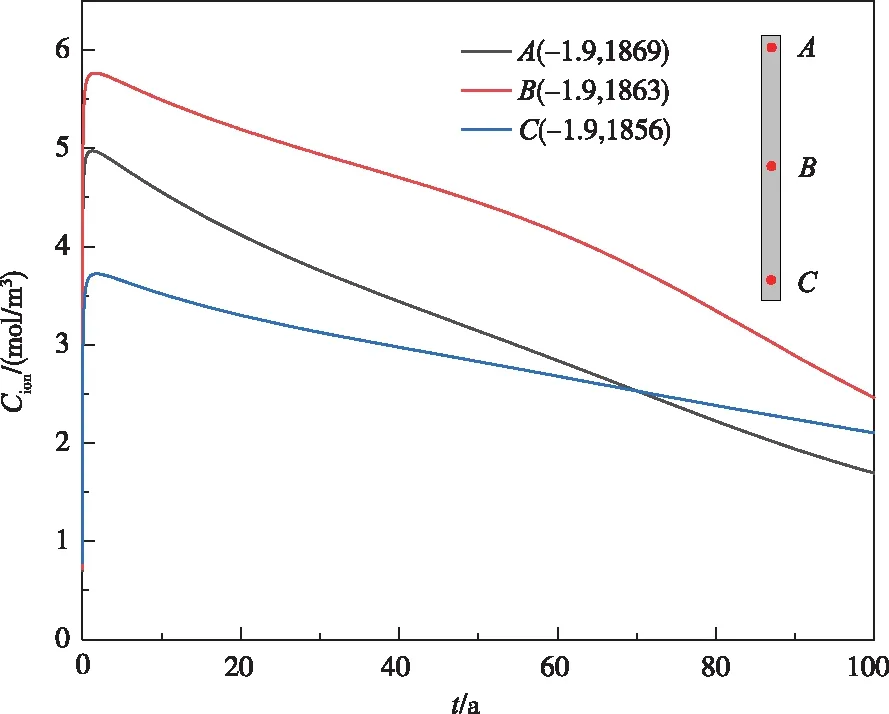
图9 典型位置钙离子浓度变化

(2)孔隙率变化。图10为防渗墙不同溶蚀时刻下的孔隙率分布图。由图10可知，随着Ca(OH)2在混凝土防渗墙中的不断溶解和地下水的迁移，防渗墙的孔隙率不断增大，运行100 a后混凝土防渗墙孔隙率约为0.33。这种变化在空间和时间上有一定差异，但由于墙体结构较薄，空间分布差异数值较小，但分布规律较明显，防渗墙顶部和底部溶蚀现象较中部严重，顶部上游侧溶蚀范围较下游侧更大，底部溶蚀深度较大。这主要是由于这些部位流速较大，且钙离子浓度较低，反应速率较大。本文混凝土防渗墙不同溶蚀时刻下孔隙率分布规律与文献[13，15]研究成果相吻合，但由于防渗体厚度及埋深有所不同，不同位置孔隙率在数值变化上存在一定差异。

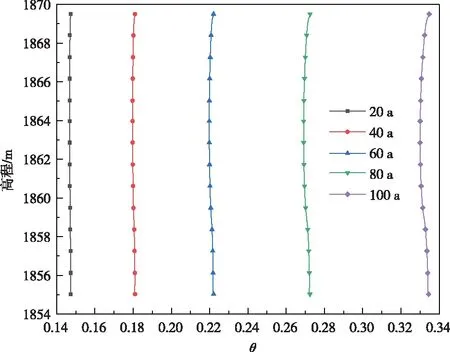
图10 不同溶蚀时刻下防渗墙孔隙率分布

(3)渗流特性。初始时刻，库水通过坝体及防渗体渗向下游，浸润线在土工膜及防渗墙处产生突变，防渗体削减水头百分比约为97.8%，削减水头作用明显，初始时刻坝体及坝基水头等势线分布如图11所示。

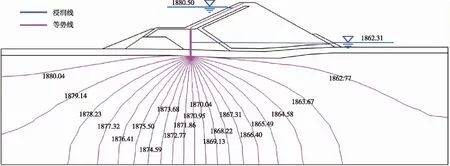
图11 初始时刻坝体及坝基水头等势线分布(单位：m)

随着溶蚀过程的发生，防渗墙内孔隙率在不断增大，孔隙率增加导致渗透系数增大，进而影响防渗墙渗流场分布。分析溶蚀对防渗墙不同区域渗透系数的影响，选取防渗墙上、中和下3个典型断面(1-1、2-2和3-3断面)，各断面不同时刻平均渗透系数变化曲线如图12所示。由图12可知，3个断面平均渗透系数均随时间呈指数型增长，且差异性较小，渗透溶蚀100 a内，渗透系数由最初的1.0×10-9m/s增长到3.6×10-8m/s，混凝土防渗墙防渗性能逐渐降低。这与流速分布关联密切，防渗墙周围地下水流速分布如图13所示。运行100 a后防渗墙渗透系数变化量级与文献[16]成果相吻合。由图13可直观看出，墙前与底部地下水渗透流速较大，最大流速约为2.5×10-5m/s，对流作用效应较大，导致这些部位钙离子浓度减少更快，溶蚀作用更强。

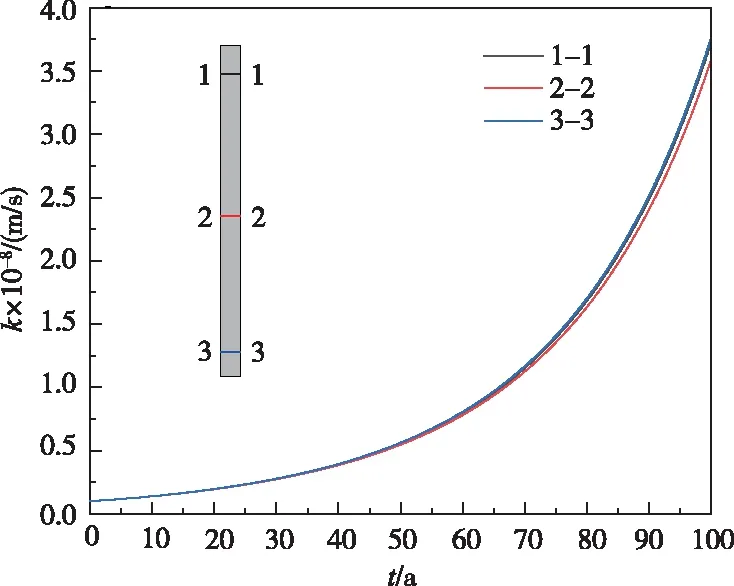
图12 典型断面不同时刻渗透系数变化曲线

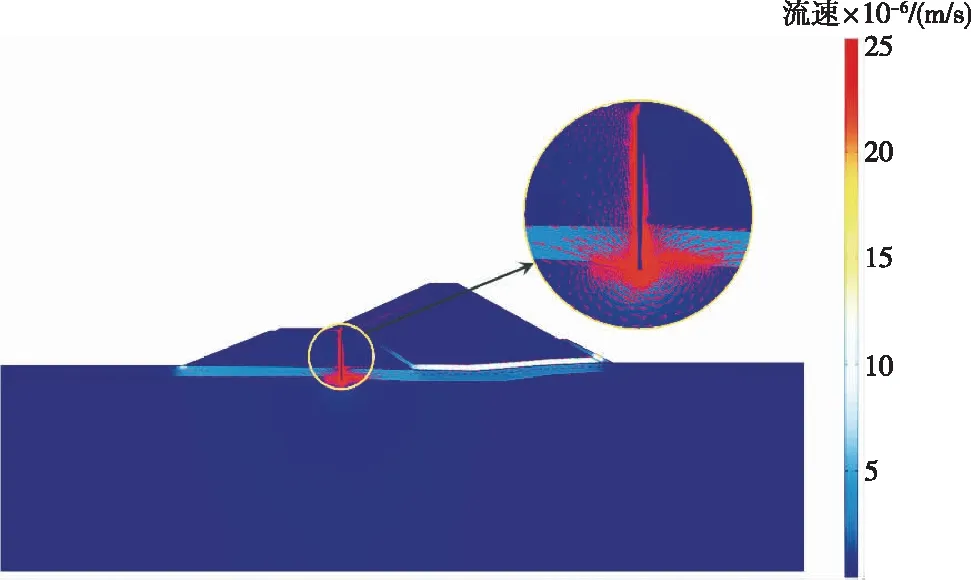
图13 地下水流速分布

随着运行时间推移，防渗墙后的浸润线不断抬升，当到达100 a时，防渗体削减水头百分比从最初的97.8%减小至95.1%。大坝渗流量也在增加，堤坝、防渗墙单宽流量及防渗墙单宽流量占比变化曲线如图14所示。由图14可以看出，流量随时间呈明显增大的趋势，初始时刻堤坝单宽流量为2.23 m2/d，运行100 a后单宽流量为3.35 m2/d，较初始时刻增大了约50%，初始时刻防渗墙单宽流量为0.04 m2/d，运行100 a 后单宽流量为1.28 m2/d，较初始时刻增大了31倍，与其防渗墙渗透系数增大倍数相当。防渗墙单宽流量占堤坝总单宽流量的百分比随堤坝运行年份增加呈指数函数增加，从初始时刻的1.6%提高至运行100 a后的38.3%，说明防渗墙渗透溶蚀对其防渗性能劣化效应随运行时间逐年增强，防渗墙防渗性能不断衰减，库区渗漏量显著增加。

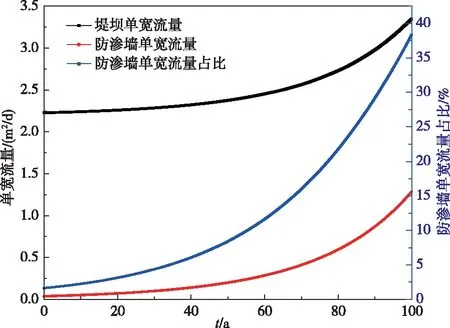
图14 堤坝、防渗墙单宽流量及防渗墙单宽流量占比变化曲线

(4)混凝土防渗墙使用年限估算。从防渗墙溶蚀和防渗性能两个方面对混凝土防渗墙使用年限进行估算，不同溶蚀时间下混凝土防渗墙中钙离子浓度和渗透系数变化曲线如图15所示。一方面结合已有文献[26]成果，将氧化钙溶出量达25%作为混凝土防渗墙溶蚀年限，本文将混凝土防渗墙中钙离子浓度峰值折减25%作为混凝土防渗墙使用年限。由图15可知，溶蚀初期，混凝土中的胶凝材料发生水化反应使得防渗墙中钙离子浓度增大，随溶蚀历时增大，水化反应逐渐减弱，在渗透水流作用下防渗墙中钙离子不断被迁移出，当防渗墙中钙离子浓度下降至峰值的75%，即3.614 mol/m3时，认定混凝土防渗墙溶蚀年限为44.0 a。

图15 防渗墙中钙离子浓度和渗透系数随溶蚀时间的变化曲线

另一方面，考虑堤坝坝基混凝土防渗墙有一定的防渗要求，防渗墙混凝土防渗等级需根据防渗墙承受的水头、墙体厚度和建筑物重要性，并满足一定安全系数储备和渗透系数要求进行设定。一般塑性混凝土防渗墙防渗等级要求比常规混凝土要低，其渗透系数一般控制在n×10-9m/s范围(n∈(1，10))，本文以1.0×10-8m/s作为混凝土防渗墙渗透系数控制指标。由图15可知，防渗墙渗透系数随溶蚀历时呈指数增加，当防渗墙渗透系数增大至1.0×10-8m/s时对应的溶蚀时间为66.4 a。

综合混凝土防渗墙钙离子迁移和渗透系数变化规律，认定该堤坝混凝土防渗墙使用年限为44.0 a。文献[26]开展了12个塑性混凝土试件长期渗透溶蚀试验，测定了塑性混凝土渗透系数和氧化钙含量，计算得出塑性混凝土防渗墙使用年限为37.1～60.7 a。新疆乌拉泊水库大坝已经运行了33.0 a，通过埋设的测压管观测，暂未发现坝基渗流异常情况，其塑性混凝土防渗墙运行良好。本文计算成果与文献[26]研究成果的变化规律和数值均较为吻合，说明本文提出的混凝土防渗墙渗透溶蚀耦合分析模型合理，适用于模拟堤坝混凝土防渗墙渗透溶蚀演化进程，研究成果亦可推广应用于土石坝坝基防渗结构长期渗透溶蚀特性分析。

5 结论

本文建立了考虑扩散-渗流-化学作用的混凝土渗流-溶蚀耦合分析模型，模拟了某复合土工膜砂砾石堤坝防渗墙渗透溶蚀进程，研究了防渗墙防渗性能演化规律，主要结论如下：(1)混凝土钙溶蚀算例表明当孔隙溶液中钙离子浓度为19.1 mol/m3时，氢氧化钙晶体完全溶解，溶蚀60、180和320 d后混凝土试件溶蚀深度分别为3.4、5.4和7.2 mm，混凝土溶蚀深度与时间的平方根呈线性关系，模型计算结果与试验测值较为一致。(2)防渗墙中钙离子浓度降低会引起防渗墙孔隙率变化，不同部位变化情况略有不同，防渗墙顶部和底部溶蚀现象较中部严重，顶部上游侧溶蚀范围较下游侧更大，底部溶蚀深度较大，固相钙溶蚀量也较高。(3)随着运行时间推移，防渗墙孔隙率不断增大，渗透系数会呈指数型增大，防渗墙后浸润线不断抬升。运行100 a后混凝土防渗墙孔隙率约为0.33，渗透系数增大了35倍，堤坝单宽渗流量增大了50%，混凝土防渗墙防渗性能显著降低。(4)结合混凝土防渗墙钙离子迁移和渗透系数成果，综合认定该堤坝混凝土防渗墙使用年限为44.0 a。本文提出的混凝土防渗墙渗流-溶蚀耦合分析模型合理，研究成果可为堤坝工程长效运行和修补加固提供理论依据。