地震波频率非平稳对土石坝非线性结构响应影响研究
张 饶,金 峰,黄杜若,刘 宁
(清华大学 水沙科学与水利水电工程国家重点实验室,北京 100084)
1 研究背景
大坝抗震分析与评价对保障工程运行安全有着重要意义,其关键问题之一是确定合理的输入地震波,不同输入地震波的结构动力反应可能差异巨大[1-3]。由于受到强震监测历史短暂和设备的限制,目前符合设计标准的实测地震波较为匮乏,人工地震波成为工程抗震设计时程分析的主要地震输入来源。现有的人工地震波合成方法主要分为物理模拟方法[4-5]、随机分析方法[6-8]和混合方法[9-10]。其中随机分析方法是一种经验校准逼近方法,利用一定数量的经验参数直接模拟生成地震波,具有所需参数少、计算成本低等优点,能在短时间内产生大量地震波,在抗震分析中应用广泛。
传统人工地震波合成方法的主要目标是将人工地震波的反应谱和设计反应谱匹配[11]。但真实地震动非常复杂,具有非平稳特征。为研究地震动频率非平稳性影响,Yeh等[12]发现时变频率对非弹性退化系统响应有显著影响。曹晖等[13]以钢筋混凝土框架为研究对象,发现如果频率成分在时间上的分布特征不同,结构的动力响应结果有着明显区别。李英成等[14]以上海某深厚覆盖场地为背景,发现地震动非平稳性对覆盖土层非线性反应的影响不容忽视。张翠然等[15]发现实际地震动与只考虑拟合反应谱的强度非平稳时程输入引起的坝体非线性反应有着较大区别。俞瑞芳等[16]对大跨度桥梁结构进行分析,发现未考虑频率非平稳性的地震动存在低估非线性结构响应的风险。因此,地震动频率非平稳性对结构动力响应,特别是非线性结构响应可能存在着重要影响。土石坝坝体及覆盖层材料在地震动反复荷载作用下,会表现出强烈的非线性特征[17-19],开展频率非平稳性对土石坝动力响应影响的研究,对土石坝抗震安全分析评价具有重要意义。
尽管地震动模拟方法得到了迅猛进展,但对具有高度非平稳性地震波的仿真模拟仍是难点,更有待发展一种精细控制地震波时-频特征以获得不同程度非平稳性地震波的模拟方法。同时,现阶段针对频率非平稳性对结构响应影响的研究,主要针对简单结构开展,对土石坝这一复杂且重要水工结构的研究仍是空白。为此本文发展了基于小波包变换(wavelet packet transform,WPT)的人工地震波随机模拟方法。同时,一方面通过精细控制人工地震波时程非平稳性、持时、谱加速度和能量累积,研究了一致频率非平稳性的人工地震波作用下土石坝结构响应的不确定性;另一方面,在控制持时、反应谱和能量累积等关键地震动参数的条件下,研究了地震波非平稳特性对考虑了边界面软化非线性本构的土石坝结构响应的影响规律。
2 基于小波包变换的地震动非平稳性刻画及人工地震波随机模拟方法
2.1 小波包分解及地震动非平稳性的刻画小波包变换在模拟生成人工地震波时具有效率高和分辨率高等优点,基于小波包变换,地震动加速度时程x(t)能以小波包的形式被分解成时间域和频率域,公式如下:
(1)

同样,根据小波包系数的分布,通过小波包逆变换,能重构得到加速度时程x(t):
(2)
Yamamoto和Baker基于小波包变换提出了一个高效的地震动随机模拟模型,根据能量大小,小波包被分别编入主要能量组和次要能量组,其中主要能量组小波包占总能量70%,次要能量组含30%,并总结出13个模型参数来刻画小波包在时-频域的分布[6]。13个统计参数分别为:Eacc代表总能量;E(t)major和E(t)minor代表主要能量组和次要能量组小波包在时间轴的形心;S(t)major和S(t)minor代表主要能量组和次要能量组小波包分布在时间轴的标准差;E(f)major和E(f)minor代表主要能量组和次要能量组小波包在频率轴的形心;S(f)major和S(f)minor代表主要能量组和次要能量组小波包分布在频率轴的标准差;S(ξ)代表次要能量组小波包幅值的离散度;ρ(t,f)major和ρ(t,f)minor代表主要能量组和次要能量组小波包在时域和频域分布上的相关性关系,反映了频率成分随时间变化的特征,能有效刻画地震动的时-频非平稳性。
主要能量组和次要能量组小波包的非平稳性参数ρ(t,f)可以通过各自小波包参数及分布,由下式分别计算得到:
(3)
式中tk和fi分别为小波包中心在时间轴、频率轴的投影位置。
如徐渭《南词叙录》对南戏的考察并没有盲从当时南戏系统已经出现的《南九宫》,而是认真考证了南宋“永嘉杂剧”阶段南戏有着“即村坊小曲而为之,本无宫调,亦罕节奏,徒取其畸农、市女顺口可歌而已”[14](P240)的体例特征,从而在这一史实基础上,推导出结论:南戏在宋元两朝其自身原本“乌有所谓九宫”[14](P240),没有宫调系统,故从明初流传至嘉靖初的《南九宫》也属“无知妄作”[14](P240)。
我们提出计算每一个时间窗格tk的平均频率,可以观察平均频率随时间的变化情况:
(4)
图1展示了两条实测地震动,其中1#地震动记录于1994年美国Northridge地震Los Angeles Baldwin Hills台站正东方向,2#地震动记录于1989年美国Loma Prietta地震Anderson dam台站。从图1(a)加速度时程很容易发现,1#地震动具有很强的非平稳性,特别是地震波后段明显存在着表面波,而图1(d)所示的2#地震波则接近平稳,地震动全程以高频成分为主。从图1(b)可以看出,1#地震波的平均频率随着时间推移呈现逐渐降低的趋势,后期平均频率小于1 Hz;而图1(e)则反映2#地震波的平均频率随时间变化几乎保持不变。从对应的小波包谱中我们更能精细观察到频率成分随着时间变化的情况,其反映的小波包时-频分布特征和前两者相同。同时,计算所得1#地震波对应的非平稳性参数ρ(t,f)major和ρ(t,f)minor分别是-0.46 和-0.36,表明非平稳性强烈;2#地震波对应的ρ(t,f)major和ρ(t,f)minor分别为-0.09 和-0.10,表明其接近平稳。参数所反映的地震波非平稳性特征和前面的分析十分吻合。

图1 两条实测地震波对比
2.2 地震动随机模拟方法黄杜若和王刚通过对小波包系数在时域和频域的调整修正,提出了一种能够实现与目标能量、反应谱相匹配的地震动随机模拟方法[7]。受此启发,作者改进了一种通过精细控制地震动小波包的时频域分布,仿真平稳、中度非平稳、高度非平稳等不同非平稳特性的人工地震波模拟方法。同时,这种方法能够根据灾害水平、场景地震直接模拟人工地震波,无需种子时程等前置条件;且同时匹配关键持时、反应谱加速度、Arias能量累积全过程等一系列重要地震动参数。
给定场景地震信息(震级Mw、距断层最近距离Rrup、剪切波速Vs30),相应的目标加速度反应谱、持时和阿里亚斯强度的分布可以通过广义条件地震动参数预测方法(GCIM procedure)得到[20-21]。目标能量累积过程引入Husid函数描述,基于选定的目标持时和阿里亚斯强度值,Husid函数通过对数正态分布的累积分布函数拟合得到[22]。此外,我们也可以基于实测地震波直接计算得到目标函数值。基于本文的研究需求,我们将实测地震波的函数值作为调整修正的目标。流程如下,流程图见图2。

图2 人工地震波模拟方法流程图
1)生成种子波。基于场景地震,通过预测方程可以获得相应小波包统计参数[7]。另一方面,基于实测地震波,可以通过小波包分布计算得到其小波包参数。根据研究所需,设置特定的非平稳性ρ(t,f)major和ρ(t,f)minor参数值,得到一系列小波包分布,通过式(2)重构得到地震动加速度时程,获得种子波库。
2)调整时域参数匹配重要持时。迭代修正小波包参数中控制时域分布的参数E(t)major,E(t)minor,S(t)major和S(t)minor,以实现重要持时t5-95的匹配。
3)调整小波包谱行向量以匹配目标反应谱。对于反应谱中特定周期的幅值,地震动中对应的频率成分对其影响最大,因此,通过迭代修正小波谱特定频率对应的行向量内容,实现和目标反应谱匹配。
4)调整小波包谱列向量以匹配能量累积过程。Husid函数描述地震动能量的累积过程[22],在每个时间步,通过迭代修正小波谱列向量内容,实现模拟地震动Husid函数值和目标值的匹配。
5)评估匹配程度。通过计算目标值和模拟值之间的误差,评估非平稳性、反应谱、Husid函数、 重要持时的匹配程度,以达到预期误差小于的3%为止。
通过以上步骤,能够得到具有特定频率非平稳性,并和目标重要持时、反应谱和能量累积过程相匹配的人工地震波。
2.3 合成地震波示例基于以上方法,我们生成了一组地震波,如图3。其中实测地震动记录于1994年美国Northridge地震Willoughby台站正东方向,以此其反应谱、能量累积过程和持时为同一目标,但目标频率非平稳性不同,合成了两条模拟地震波,分别为克隆模拟地震波和对比模拟地震波。克隆波预期与目标实测波保持相同的频率非平稳性,对比波则预期接近平稳。

图3 实测地震波、克隆组模拟地震波和对比组模拟地震波示
从地震动加速度时程和小波包谱的特征容易观察到,实测地震波具有较为强烈的时-频非平稳性,非平稳性参数ρ(t,f)major和ρ(t,f)minor分别为-0.44和-0.40。克隆地震波很好的保持了实测波的非平稳特性,ρ(t,f)major和ρ(t,f)minor分别为-0.47和-0.44。对比地震波则接近平稳,从地震初期到末期均是高频成分占主要内容,且小波包分布离散,参数ρ(t,f)major和ρ(t,f)minor分别为-0.15和-0.07。此外,三条地震波的能量累积过程和加速度反应谱匹配良好,但频率随时间的变化有所不同。
3 土石坝模型
Success土石坝位于美国加州图里河,是一座碾压式土石坝。最大坝高44.2 m,坝顶长1037.5 m,坝顶宽6.8 m,坝体由心墙、填土区和过渡区组成。研究中选取典型横截断面,上下游由可透水的砂土填充,心墙为不透水的砂质黏土和黏土沙,在心墙和填土之间设置了砂砾土组成的过渡区。河床冲积层根据土层年代和土体特性,分为新覆盖层和老覆盖层。新覆盖层为砂土以及含少量鹅卵石的砂砾石,可液化,厚度4.5 m。参考美国陆军工程兵团报告[23]获得可归一化剪切波速值[24]、标准贯入试验锤击数修正值(N1)60(简称标贯修正值)等材料参数,如表1所示。

表1 土石坝材料特性

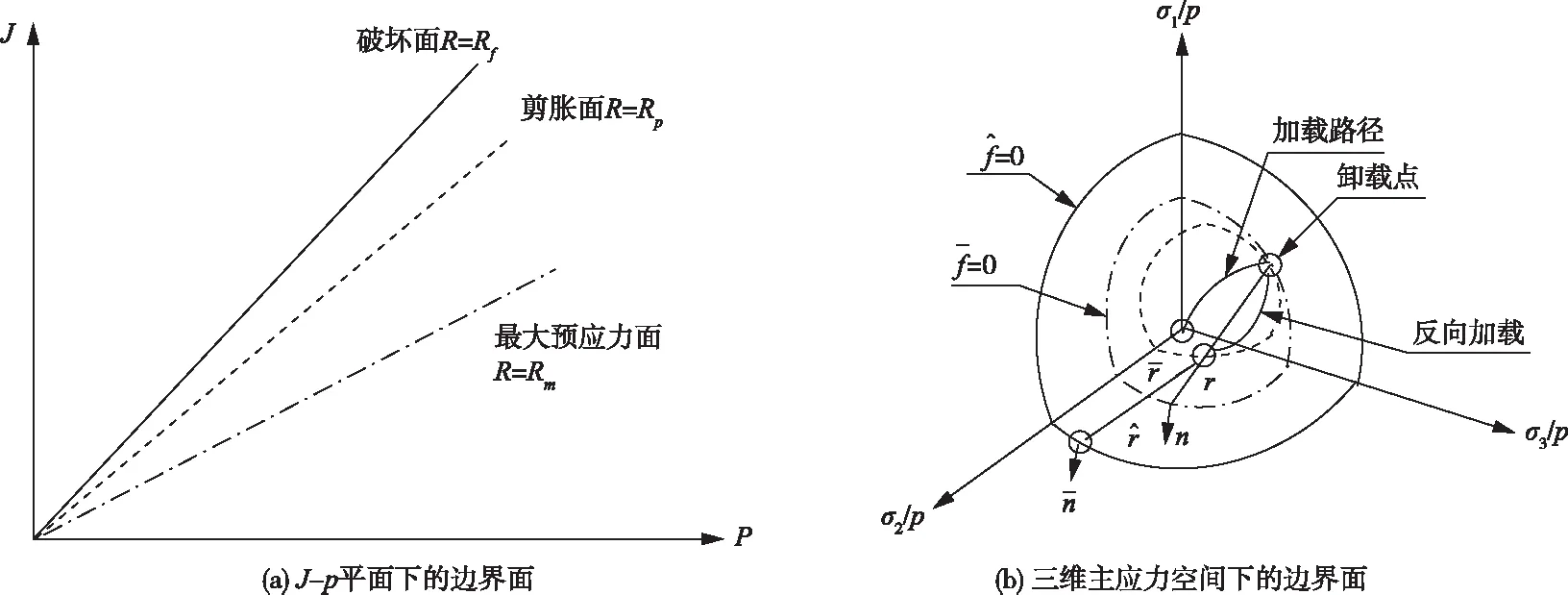
图4 边界面亚塑性模型的边界面[25]
本构模型中共有8个控制参数,分别为:φ,等效摩擦角,用于定义极限破坏状态面;G0,初始模量系数,控制初始最大模量;hr,刻画剪切模量和剪切应变的振幅非线性关系的参数;kr,控制单调加载条件下有效应力变化的参数;b,用于改变有效应力路径形状的参数;d,控制不排水条件孔隙水压变化或排水条件下因剪切引起的体积变化的参数,刻画土体抵抗液化能力;κ,刻画土体压缩性的参数;Rp,表征相变线的参数。各参数值参考了美国陆军工程兵团报告取值[23],如表2所示。
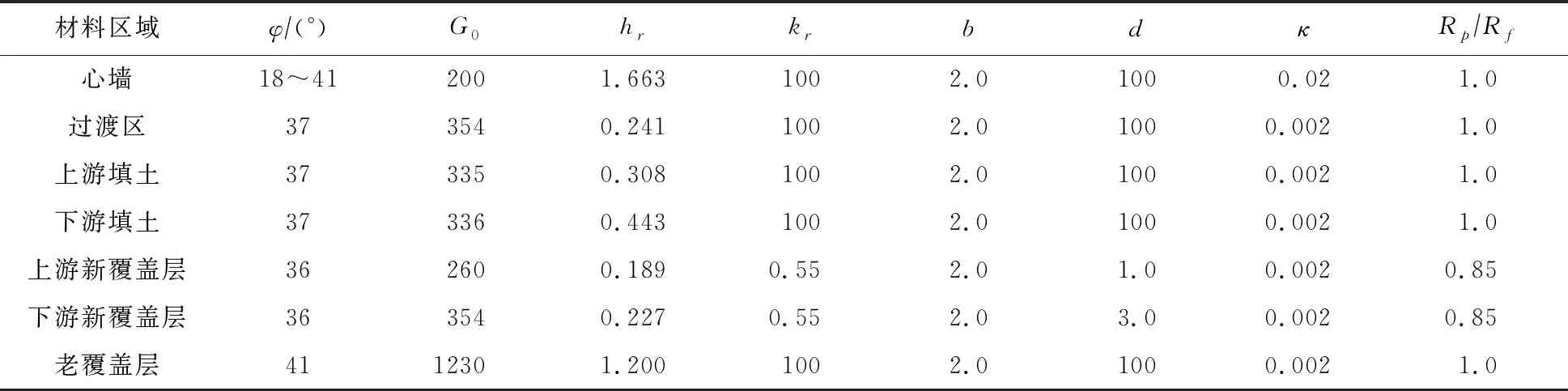
表2 边界面亚塑性本构模型参数取值
通过FLAC软件建立了大坝模型,主体模型如图5。在模型边界上设置了自由场边界条件[27],主体网格和自由场网格之间设置阻尼器,模拟与无限地基相同的地震波传播效果,并考虑了材料瑞利阻尼比为0.02。
静力计算中重力通过分层施加方式完成,并考虑了库水影响,将最终应力场和渗流场作为震前初始状态。动力计算中采用位移-压力(u,p)方式求解地下水渗流条件下的流固耦合作用[27]。大坝响应分析了新覆盖层土体有效应力发展路径、剪应力-应变关系,以及变形较大区域的节点位移,即坝顶节点、坝址下游节点、坝址上游节点,节点分布如图5中红色虚线框内所示。
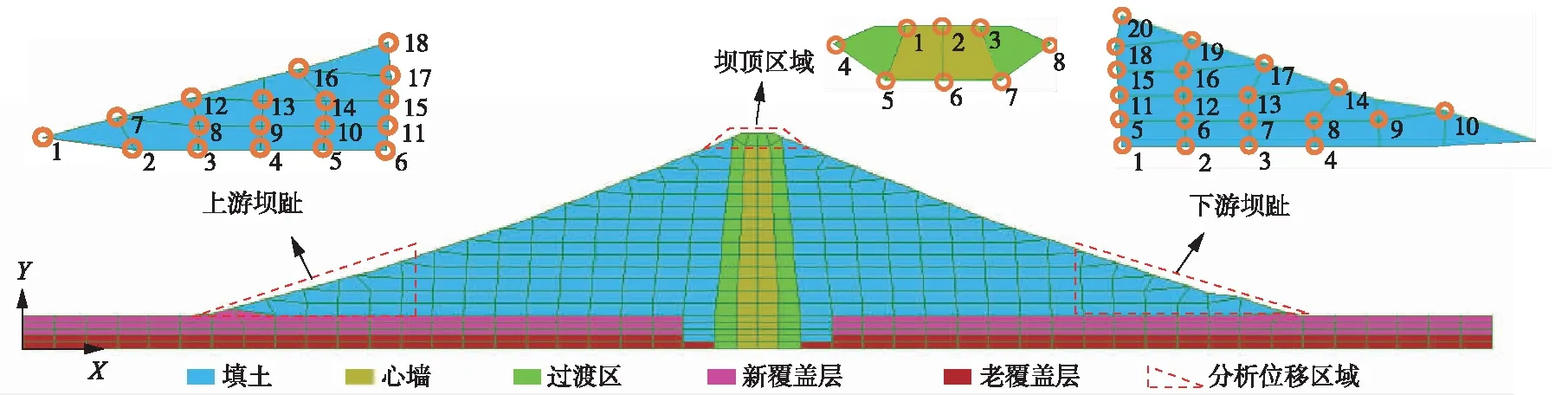
图5 大坝有限差分模型
4 基于一致频率非平稳性地震波输入的土石坝结构响应离散性
4.1 地震波数据集以1994年美国北岭地震Los Angeles Baldwin Hills台站正北方向实测地震波为目标,模拟生成了与实测地震波的频率非平稳性、加速度反应谱、能量累积过程和重要持时等相匹配的15条人工地震波。图6绘制了实测地震波的加速度时程、能量累积过程和加速度反应谱图。图7展示了15条人工地震波的加速度时程,以及人工波与实测波的反应谱和能量累积过程的匹配情况。可以看出,实测地震波和15条人工波的波形相似,且均具有较为明显的时-频非平稳性,在地震动前20 s内以高频纵波为主,而在25~40 s则有着较丰富的低频成分,明显有表面波的存在。在图7(d)(e)反应谱和能量累积匹配对比图中,无论是对极值的控制还是对曲线形状的精细刻画,15条人工地震波均与实测地震波均匹配良好。

图6 目标实测地震波

图7 人工地震波组
实测地震波和15条人工波的非平稳性参数ρ(t,f)major和ρ(t,f)minor见表3。实测波分别为-0.52,-0.34,反映其小波包分布具有明显的时-频相关性,地震动具有较强烈的非平稳性。15条人工地震波的ρ(t,f)major均值为-0.52,ρ(t,f)minor均值为-0.40,和目标实测波非常一致,且标准差很小,小于0.05。地震波数据集15条人工地震波很好地控制了反应谱、能量累积过程等地震动参数,且具有一致的频率非平稳特征。

表3 实测波与人工地震波组非平稳性特征
4.2 土石坝动力响应
4.2.1 平均有效应力路径和剪应力-应变关系 在新覆盖层的上下游随机选择部分单元,分析其在动力计算下的有效应力路径和剪应力-应变关系。从15组计算结果中发现,随着单元平均有效应力从初始应力状态到触发液化(平均有效应力小于14.35 kPa[26]),剪应力-应变路径都会逐渐软化,剪应变逐渐增加。特别地,15组的有效应力路径和剪应力-应变回环路径均非常相似,且最大剪应变十分接近。
图8展示了位于第15列、第4行的(15,4)单元,在3组人工波作用下的应力-应变关系。从图8(a)看出,该单元在不同地震动作用下,平均有效应力的发展路径非常相似,初始阶段变化较为缓慢,后期剧烈,且都到达了触发液化的有效应力水平。图8(b)可以看出,单元的剪应力-应变变化曲线虽略有区别,但规律非常一致,且回环曲线很相似,最大剪应变十分接近,约为6.5%。因此,在一致频率非平稳性地震波的作用下,坝体土体单元的应力应变关系存在一定的离散性,但离散程度低。

图8 新覆盖层单元在不同地震波作用下的应力应变关系
4.2.2 最大位移响应 动力计算中,土石坝容易发生大位移的区域为坝顶和上下游坝趾。本小节分析坝顶最大沉降位移、下游坝趾偏下游和上游坝趾偏上游的最大水平位移。分别得到15条地震波作用下的最大位移分布以及离散性,离散性通过变异系数衡量,公式如下:
(5)
式中:σ为节点最大位移分布的标准差;μ为最大位移平均值。
图9展示了土石坝坝顶两层单元内8个节点的最大沉降位移响应。图9(a)为表征最大位移分布的箱线图,分别统计了均值、极值、中位数及上下四分位数。可以发现,坝顶区域发生了很大的沉降,但沉降不均匀。心墙中心处的节点(2号、6号节点)最大沉降位移超过了4 m,心墙和过渡区交界的节点(如5号和7号)最大沉降位移超过2 m,相邻节点间发生不均匀沉降的主要原因是材料属性不同,动力响应不同。心墙土体有效摩擦角小,材质松软,摩擦角决定了破坏状态面,土体单元易发生大塑性变形;过渡区摩擦角大,材质更坚硬,变形更小。但一致地,各节点的最大位移分布较集中,均分布在均值附近。图9(b)为各节点最大位移的变异系数统计图,其值分布在10%左右,最小值约为8%,反映最大沉降位移分布离散程度低。
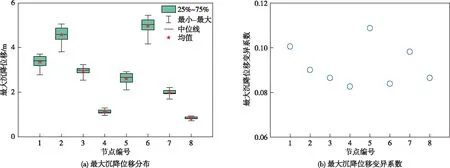
图9 坝顶节点最大沉降位移分布及变异系数图
图10展示了下游坝趾区域20个代表节点偏向下游的最大水平位移响应。从图10(a)箱线图可以看出,坝体下游坝趾区域发生了较大的水平位移,各节点最大位移均值均超过2 m,但各节点的最大水平位移分布较集中。图10(b)了各节点最大位移的变异系数统计图,变异系数值不超过8%,反映下游坝趾区域最大水平位移响应的离散性弱。

图10 下游坝趾最大水平位移分布及变异系数图
图11展示了上游坝趾区域18个代表节点偏向上游的最大水平位移响应。图11(a)为最大水平位移分布的箱线图。相较坝顶和坝体下游坝趾区域,上游坝趾区域发生的最大位移较小,主要是考虑了库水压力的作用。各节点最大位移均值分别在0.5~1 m之间,各节点的最大水平位移分布集中。图11(b)为各节点最大位移的变异系数统计图,发现变异系数值小于10%,反映最大水平位移分布的离散程度低。
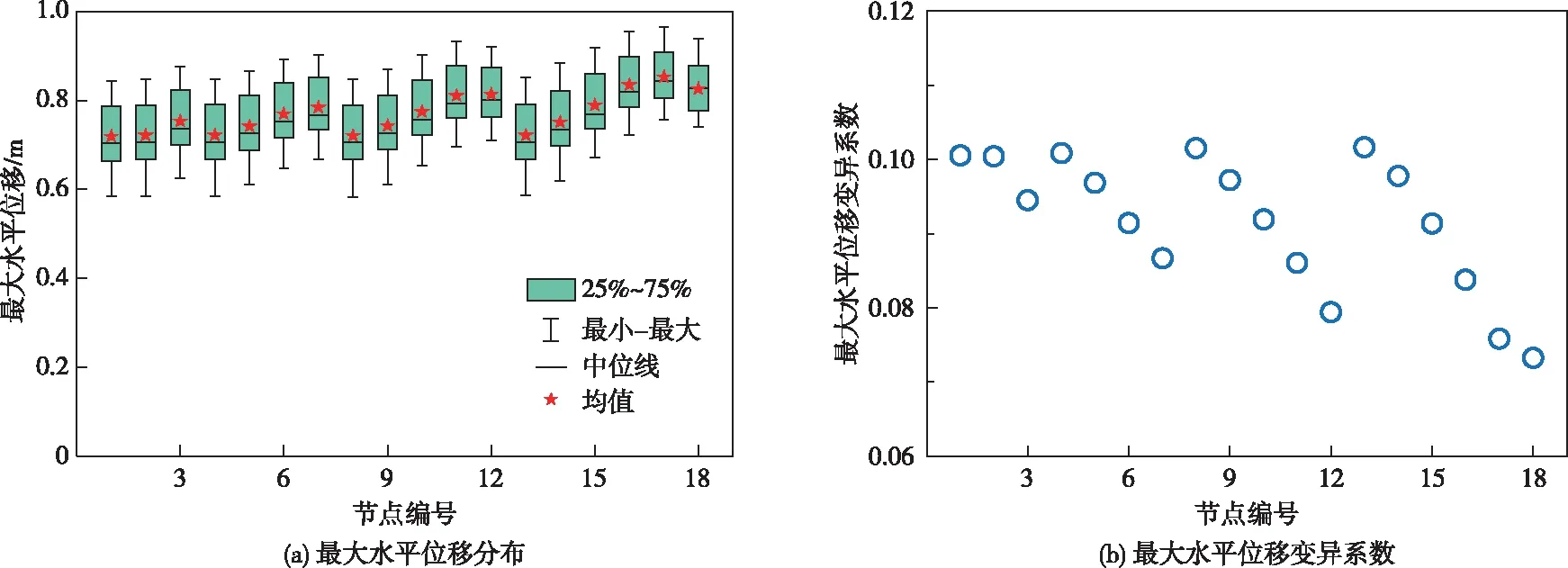
图11 上游坝趾最大水平位移分布及变异系数图
5 不同频率非平稳性地震波作用下的土石坝坝体响应分析
5.1 实测与模拟地震波数据库从1971年San Fernando地震、1979年Imperial Valley地震、1989年Loma Prieta地震、1994年Northridge地震和1999年我国台湾集集地震共5场历史大震中,选择了17条实测地震动记录,其均具有较为强烈的时-频非平稳特征。以实测地震波为目标,通过上述人工地震波合成方法,生成了两组人工地震波:克隆模拟地震波组、对比模拟地震波组,每组波17条。克隆组地震波与实测波保持了相同的频率非平稳性、反应谱、能量累积过程和重要持时等特征;对比组地震波和实测地震波匹配相同反应谱、能量累积过程和重要持时,但频率非平稳性明显不同,该组地震波均接近平稳。示例地震波如第一节中的图3所示。
图12将两组模拟地震波的阿里亚斯强度Ia、重要持时t5-95以及非平稳性参数ρ(t,f)major和ρ(t,f)minor同实测地震波组进行了对比。在图12(a)(b)中,克隆组与对比组模拟地震波的Ia和t5-95值几乎落在1∶1直线上,表明模拟地震波能够很好地与实测地震波的这些特征相匹配。针对地震动非平稳特性表征量ρ(t,f)major和ρ(t,f)minor,我们从图12(c)(d)可以看出,克隆组模拟地震波的数据值都落在1∶1直线附近,表明其值与实测地震波更接近,非平稳特征接近;对比组模拟地震波的数据值都远离1∶1直线,表明其值与实测地震波相差较远,非平稳特征差别大,且其值在0附近,表明其接近平稳。

图12 实测组、克隆组和对比组模拟地震波的阿里亚斯强度、重要持时、非平稳性参数对比图
5.2 基于实测和模拟地震波数据集的土石坝动力响应分析本节主要研究了地震动频率非平稳性对土石坝非线性结构响应的影响。利用5.1节中的地震波作为输入,以Success土石坝为例,分别将克隆组波、对比组波的计算结果同实测波组的计算结果进行对比,研究模拟地震波对土石坝非线性结构响应无偏估计的性能区别。为了量化不同数据集的性能优劣,定义了残差来衡量模拟波组结果和实测波组结果的差异,其计算公式如下:
Residual=ln(S模拟波)-ln(S实测波)
(6)
式中:S为最大位移响应;下标为动力计算结果的所属地震波组。
图13展示了坝体大变形区域最大位移的残差均值统计,图13(a)为坝顶区域,图13(b)为上游坝趾区域,图13(c)为下游坝趾区域。特别说明的是,根据第4节位移均值结果,以及本小节计算发现,坝顶的最大沉降位移值要大于上/下游坝趾水平位移值,且以上游坝趾水平位移值最小。从图13很容易看出,克隆波组地震波对各个区域的位移响应无偏估计效果很好,残差均值均接近0。对比波组的残差均值则在-25%至-10%之间,且对于位移更大的坝顶和下游坝趾区域,其残差均值的绝对值更大。表明对比波组相较于实测波组,会较大程度上低估坝体结构动力响应,且对于变形越大的区域,其低估程度越高。计算结果表明控制频率非平稳性,对结构响应有着更好的无偏估计;另外,平稳地震波会低估坝体响应,其对坝体非线性响应的激励作用更弱,且土体变形越大的区域,其激励效果和非平稳地震波的差别越大。

图13 坝体节点最大位移的残差均值图(克隆波组;对比波组)
6 结论
本文发展了基于小波包变换的人工地震波合成方法,生成了一系列人工地震波。该类地震波能与目标加速度反应谱、能量累积过程和重要持时等特征匹配良好,且具有特定的频率非平稳性。在同时控制反应谱、能量累积过程和持时等地震动参数后,具有一致频率非平稳性的不同人工地震波输入得到的土石坝非线性结构响应结果接近,主要表现为土体单元的平均有效应力发展路径和剪应力-应变关系十分相似,坝体大变形区域的最大位移响应分布较集中、其变异系数小于10%。
在控制了地震波的反应谱、能量累积过程和持时后,频率非平稳性对土石坝非线性结构响应影响显著。控制模拟地震波的频率非平稳性,对土石坝结构响应有着更好的无偏估计效果,模拟波组与实测波之间的最大位移十分接近,残差均值约为0。而未控制频率非平稳性的平稳模拟地震波,对土石坝结构响应无偏效果较差,会较大程度上低估坝体响应,残差均值的极值能达到-25%,且对土体变形越大的区域,其激励效果和非平稳地震波的差别越大。在水利工程设计中,工程师们或许应对地震动频率非平稳性给予足够的重视和考虑。

