利用构造函数法求解导数不等式问题

魏立向

(甘肃省定西市安定区交通路中学)

不等式求解问题是高考的重点内容,利用函数单调性证明不等式问题是近几年高考的热点和难点.若在一个不等式中同时含有f(x)与f′(x),常通过构造辅助函数来求解,即构造一个含有f(x)与另一函数g(x)的积或商的新函数F(x)来解题.

根据函数的求导法则,构造辅助函数经常要用到以下几种常见的数学模型.

构造差函数对于不等式f′(x)－g′(x)≥0,构造函数F(x)＝f(x)－g(x).特别地,对于不等式f′(x)≥k,构造函数F(x)＝f(x)－kx.

构造积函数1)对于不等式f′(x)g(x)＋f(x)g′(x)≥0,构造函数F(x)＝f(x)g(x).

2)对于不等式xf′(x)＋nf(x)≥0,构造函数F(x)＝xnf(x).

3)对于不等式f′(x)＋f(x)≥0,构造函数F(x)＝exf(x).

4)对于不等式f′(x)＋kf(x)≥0,构造函数F(x)＝ekxf(x).

构造商函数1)对于不等式f′(x)g(x)－f(x)g′(x)≥0,构造函数,则

1 构造差函数F(x)=f(x)-g(x)

例1已知函数f(x)为R上的偶函数,f′(x)是f(x)的导函数,且当x∈[0,＋∞)时,f′(x)＞2x.若f(a－1)－f(a)≥1－2a,求实数a的取值范围.

令F(x)＝f(x)－x2,因为f(x)为R 上的偶函数,所以F(x)为R 上的偶函数,且F′(x)＝f′(x)－2x.又因为当x∈[0,＋∞)时,F′(x)＝f′(x)－2x＞0,所以F(x)在[0,＋∞)上是增函数.又因为F(x)为R 上的偶函数,所以F(x)在(－∞,0)上是减函数.

f(a－1)－f(a)≥1－2a等价于f(a－1)－1＋2a－a2≥f(a)－a2,即f(a－1)－(a－1)2≥f(a)－a2,则F(a－1)≥F(a),所以|a－1|≥|a|,解得a≤,故a的取值范围是

2 构造积函数F(x)=xnf(x)

例2已知y＝f(x)是定义在R上的奇函数,且当x＜0时,不等式f(x)＋xf′(x)＜0成立,若a＝20.3·f(20.3),b＝logπ3·f(logπ3),,试判断a,b,c的大小关系.

设F(x)＝xf(x),则F′(x)＝f(x)＋xf′(x),结合已知可得当x＜0时,F′(x)＜0,故F(x)在(－∞,0)上单调递减.

由y＝f(x)为R 上的奇函数知F(x)＝xf(x)为R上的偶函数,所以F(x)在(0,＋∞)上单调递增,所以

又0＜logπ3＜1＜20.3＜3,所 以F(logπ3)＜F(20.3)＜F(3),即b＜a＜c.

3 构造商函数

例3已知函数f(x)是定义在(－∞,0)∪(0,＋∞)上的偶函数,f′(x)是函数f(x)的导函数,若∀x＞0,都有xf′(x)－2f(x)＞0 成立,试比较9f(－2)与4f(3)的大小.

又因为函数f(x)是定义在(－∞,0)∪(0,＋∞)上的偶函数,则F(x)为(－∞,0)∪(0,＋∞)上的偶函数,故F(－2)＝F(2),结合F(2)＜F(3),则F(－2)＜F(3),故即9f(－2)＜4f(3).

4 取对数法构造形似函数

例4求证:当m＞n＞0时,有(e＋m)e＋n＜(e＋n)e＋m成立.

证明当m＞n＞0时,要证不等式(e＋m)e＋n＜(e＋n)e＋m成立,只需证(e＋n)ln(e＋m)＜(e＋m)·ln(e＋n)成立,即证成立.

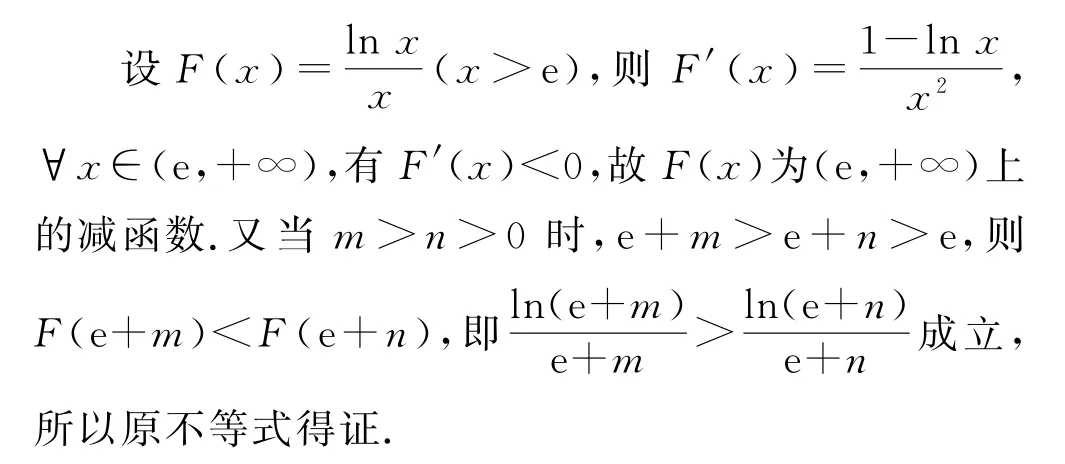
5 移项法构造二阶导函数

例5已知函数f(x)＝2aex－x2.

(1)若f(x)为R 上的增函数,求实数a的取值范围;

(2)若a＝1,求证:∀x＞0,f(x)＞2x＋2成立.

(1)由f(x)＝2aex－x2(x∈R),得f′(x)＝2aex－2x(x∈R),因为f(x)为R 上的增函数,所以f′(x)≥0在R上恒成立,即2aex－2x≥0在R上恒成立,即

综上,a的取值范围是

(2)当a＝1,x＞0时,f(x)＝2ex－x2(x＞0),要证当a＝1 时,∀x＞0,f(x)＞2x＋2 成立,只需证f(x)－(2x＋2)＞0(x＞0)恒成立,即证2ex－x2－2x－2＞0(x＞0)恒成立.

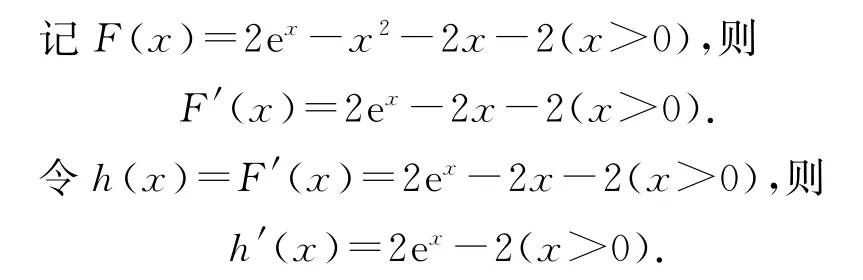
显然,当x＞0时,h′(x)＞0,h(x)在(0,＋∞)上单调递增.又h(x)在x＝0处连续,h(x)＞h(0)＝0,即F′(x)＞0,F(x)在(0,＋∞)上单调递增.

又F(x)在x＝0处连续,F(x)＞F(0)＝0,即

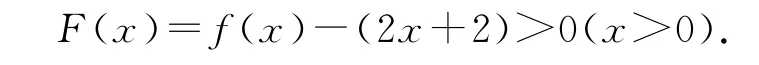
综上,当a＝1时,∀x＞0,f(x)＞2x＋2成立.

总而言之,利用构造函数法求解导数不等式问题的关键在于充分挖掘题中的条件,构造合适的辅助函数,与题设形成解题链条,再将不等式的求解问题转化为研究辅助函数的单调性和最值问题,进而可解原不等式.

链接练习

1.定义在R 上的函数f(x)满足f′(x)＋f(x)＞1,f(0)＝3,则不等式exf(x)＞ex＋2的解集为( ).

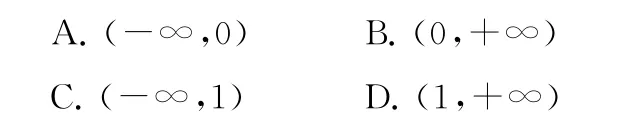
2.定义在R 上的函数f(x)满足f(1)＝2,且对任意的x∈R有f′(x)＜1,则不等式f(x2)＞x2＋1的解集是( ).

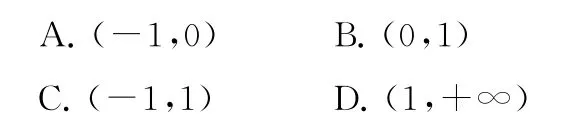
3.设f′(x)是奇函数f(x)(x∈R)的导函数,且f(2)＝0,当x＞0时,xf′(x)－f(x)＜0,使得f(x)＞0成立的x的取值范围是( ).

链接练习参考答案

1.B. 2.C. 3.D.

(完)