基于刚度定向的工业机器人铣削姿态优化研究

杨 靖 张小俭 吴 毅 叶松涛 严思杰， 陆家麟

1.华中科技大学机械科学与工程学院，武汉，4300742.华中科技大学无锡研究院，无锡，2141743.固瑞特模具(太仓)有限公司，苏州，215488

0 引言

飞机机翼蒙皮、发电机及船用螺旋桨桨叶等大型复杂曲面类零件在国家高端装备领域广泛应用。这类零件尺寸大、结构复杂、加工可达性差，传统数控机床由于加工行程的制约，往往无法适应其制造和装配需求。相对而言，工业机器人操作空间大、灵活性强，因此机器人加工在航空、航天以及船舶等领域备受青睐。但工业机器人结构刚度较低，铣削加工过程中容易发生颤振，难以保证铣削稳定性。

TOBIAS等[1]和TLUSTY等[2]最早指出，再生效应和模态耦合效应是引起加工颤振的主要机制。由于模态耦合颤振很少发生在刚度较大的数控机床上，故对传统加工颤振的研究主要聚 焦于镗杆、铣刀等刀具的再生颤振。与传统机床不同，串联结构导致工业机器人刚度较低，使用机器人加工必须考虑模态耦合颤振的影响。近年来，学者们对加工过程中的颤振问题开展了广泛的研究，但与模态耦合颤振相关的报道较少。GASPARETTO[3]通过建立刀具-工件系统的数学模型，从理论上解释了模态耦合颤振机理。PAN等[4-5]在机器人铣削实验中观察到严重的低频颤振现象，基于动力学模型分析发现切削力方向与工业机器人主刚度方向之间的夹角是影响加工过程稳定性的主要因素，并建立了模态耦合颤振的预测准则。基于前人的工作，CEN等[6]将保守同余变换(conservative congruence transformation，CCT)应用到机器人铣削颤振分析中，提出优化机器人进给速度可以避免铣削过程中的模态耦合颤振。虽然以往研究[4-6]表明，改变切削力方向与工业机器人主刚度方向之间的夹角可以抑制颤振，但如何得到工业机器人的主刚度方向报道较少。HE等[7]首次提出了一种将模态振型和工业机器人运动学相结合的刚度定向方法，但需要应用有限元软件辅助分析。同时，工业机器人的功能冗余特性一直是研究的热点。学者们定义了不同的冗余优化标准，如刚度性能指标最大化[8]、稳定性边界最优化[9-10]等，但利用工业机器人功能冗余改变姿态、避免模态耦合颤振的研究未见报道。

本文提出了一种刚度定向方法，利用刚度椭球计算机器人加工系统在切削平面内的主刚度方向，操作过程简单；针对模态耦合颤振抑制，研究如何利用功能冗余优化工业机器人姿态。

1 机器人铣削模态耦合颤振机理

1.1 机器人铣削动力学建模

为了研究工业机器人铣削过程中的模态耦合颤振，首先建立切削坐标系{c}和主刚度坐标系{k}，如图1所示。同时，作以下假设[4]来简化分析：①阻尼效应总是提高系统的稳定性，为了降低复杂度，仅考虑无阻尼系统；②铣削力大小与其他参数无关，只与径向切削深度成正比。

基于上述假设，在切削坐标系中建立无阻尼二自由度铣削动力学模型：

(1)

x=[xcyc]T

(2)

式中，x为刀尖点在xc和yc方向上的位移；M、K分别为2×2质量和刚度矩阵；Kp为过程刚度矩阵；kp为切削刚度；β为切削力F与xc轴夹角。

本文重点在于研究刚度方向对模态耦合颤振的影响，不失一般性，假设质量矩阵M为对角阵，且对角元素相等。根据ALTINTAS[11]提出的平均铣削力模型，作用在铣刀上进给方向(xc方向)、法向(yc方向)的切削力分量分别为

(3)

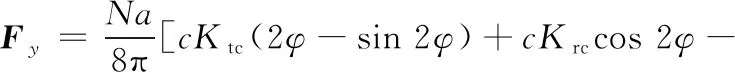
(4)

式中，N为铣刀齿数；a为轴向切削深度；c为进给率；φ为刀齿的瞬时齿位角；Ktc、Krc分别为切向和径向切削力的剪切力系数；Kte、Kre分别为刃口力系数；φst、φex分别为刀具的切入角和切出角。

根据式(3)和式(4)给出的切削力分量，可以计算出切削力F与xc轴夹角β，β=arctan(Fy/Fx)。

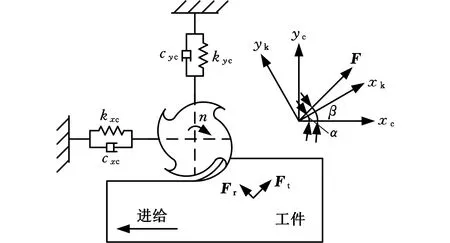
图1 铣削加工模型Fig.1 Mechanical model of milling

1.2 铣削过程稳定性分析

为了解耦式(1)，需要将其由切削坐标系{c}转换至主刚度坐标系{k}中。由图1可知两个坐标系之间满足：

(5)

其中，α为xc轴和xk轴之间的夹角。设定：

(6)

将式(5)代入式(1)并对式(1)进行解耦：

(7)

对式(7)进一步计算可得

(8)

其中，mq为模态质量；kx、ky分别为xk和yk方向的模态刚度；γ为切削力F与xk轴夹角，γ=β-α。整理式(8)可得

(9)

记k′x=kx-kpsinαcosγ，k′y=ky-kp·cosαsinγ[5]，则式(9)的特征方程为

(10)

进一步计算可得

(11)

若λ2均为负实数，则加工过程稳定；而当λ2存在虚数时，则产生模态耦合颤振[12]。机器人加工系统的结构刚度kx、ky一般远大于切削刚度kp，因此，式(11)中的-(k′x+k′y)一定为负数。此时只需要分析式(11)中根号内的部分，即可判定系统稳定性。

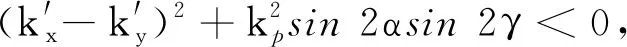
2 机器人加工系统刚度定向方法

2.1 机器人加工系统运动学模型

本文的理论分析及实验均基于ABB公司的IRB 6660-130/3.1型号工业机器人。进行刚度定向之前，需要对机器人加工系统进行运动学分析。采用修正的D-H方法建立了ABB IRB6660工业机器人的运动学模型，为每个连杆建立坐标系{i}，如图2所示，其中，坐标系{t}为工具坐标系。基于该运动学模型，可以分析任意连杆之间的位姿关系，获得工业机器人从基座到末端的齐次变换矩阵T0t，同时计算机器人加工系统的雅可比矩阵。相应坐标系下机器人的D-H参数见表1。

表1 IRB 6660-130/3.1机器人D-H参数

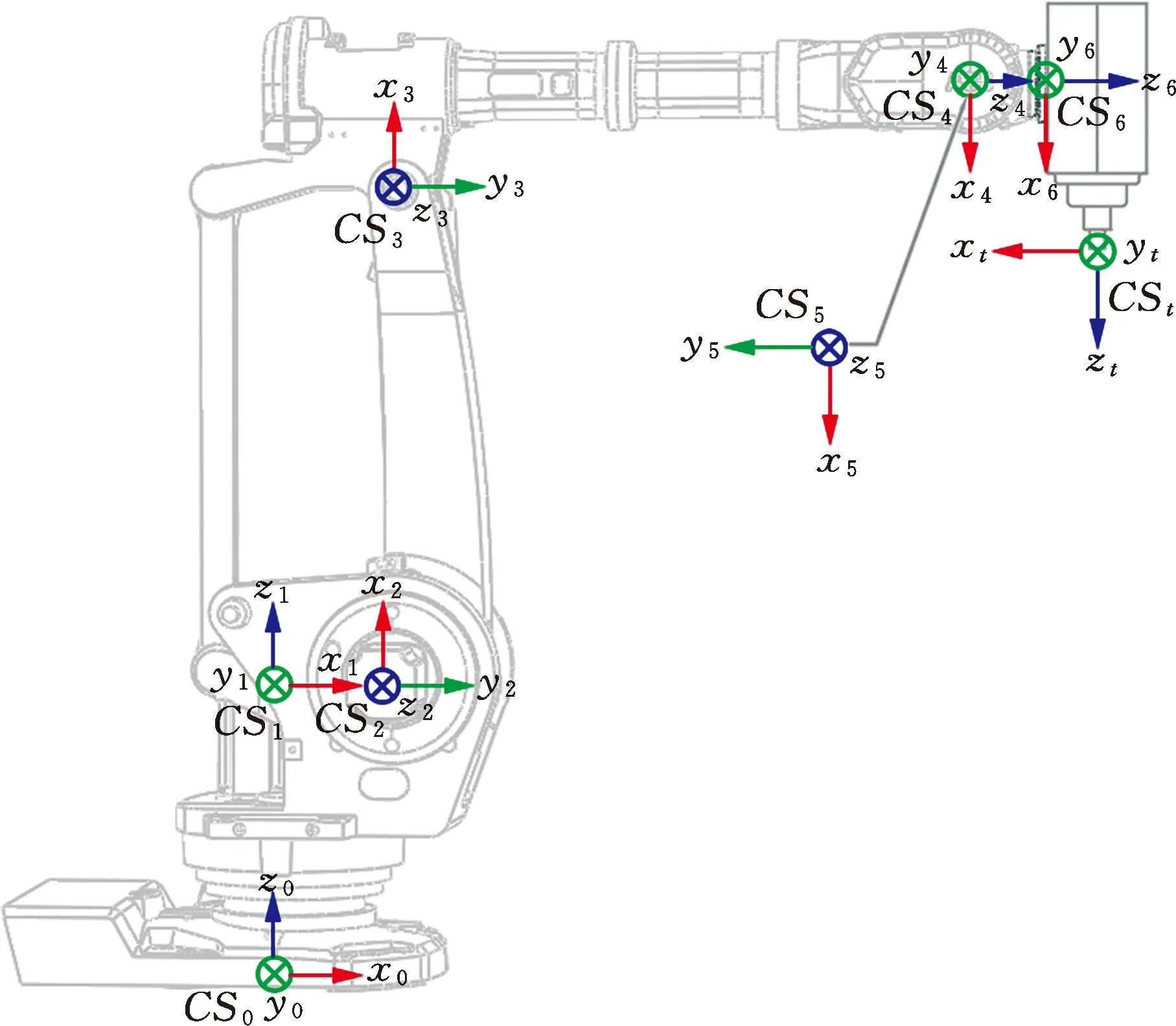
图2 IRB 6660-130/3.1机器人D-H模型Fig.2 D-H model of the IRB 6660-130/3.1 robot

2.2 刚度定向方法

在铣削加工中，完整的机器人铣削系统包括工业机器人本体、安装在末端法兰的电主轴及铣刀。由上文稳定性分析可知：角度α和γ是决定加工过程是否稳定的重要因素。确定这两个角度需要获得机器人在加工平面内的主刚度方向，但机器人加工系统的非对称结构导致其主刚度方向不易确定，因此，本文提出一种基于工业机器人刚度椭球的主刚度定向方法。机器人末端刚度椭球作为评价机器人在整个笛卡儿空间内的综合刚度性能指标，其各个方向上的轴长直接反映了机器人末端在对应方向上的刚度，因此通过计算刚度椭球在切削平面内的长轴和短轴方向，即可确定工业机器人主刚度方向。具体步骤如下：

剥夺他人生命的形式有很多种，法律对具体的行为方式不做限制。既可以暴力手段，也可以是非暴力手段；既可以是作为方式，也可以是不作为方式。[4]10-11因艾滋病的病情的特殊性，故意传播艾滋病符合故意杀人罪的客体特征。

(1)进行工业机器人关节刚度辨识实验[13]，求出其关节空间刚度矩阵Kθ，并通过矩阵Kθ与末端笛卡儿空间刚度矩阵K之间的映射关系，获得机器人笛卡儿刚度矩阵K。

(2)利用刚度矩阵K中的力-线位移子矩阵Kft(3×3)计算出机器人加工系统末端的刚度椭球，并将其在切削坐标系中表示。

(3)刚度椭球与切削平面相交面为椭圆面，通过求取该椭圆长轴及短轴方向，即可获得机器人加工系统在特定位姿下，切削平面内的最大刚度方向和最小刚度方向。

通过实验得到的工业机器人各关节刚度值见表2。在关节空间中，每个关节的刚度是相互独立的。

表2 IRB6660机器人关节刚度

通过雅可比矩阵将关节刚度矩阵转化至笛卡儿空间[14]：

K=J-TKθJ-1

(12)

其中，J为相对切削坐标系{c}表示的雅可比矩阵；Kθ为关节空间刚度矩阵，Kθ=diag(Kθ1，Kθ2，…，Kθ6)；K为6×6笛卡儿空间刚度矩阵，可以将其划分成4个3×3子矩阵：

(13)

式中，Kft、Kfr、Kmt、Kmr分别为力-线位移子矩阵、力-角位移子矩阵、力矩-线位移子矩阵和力矩-角位移子矩阵。

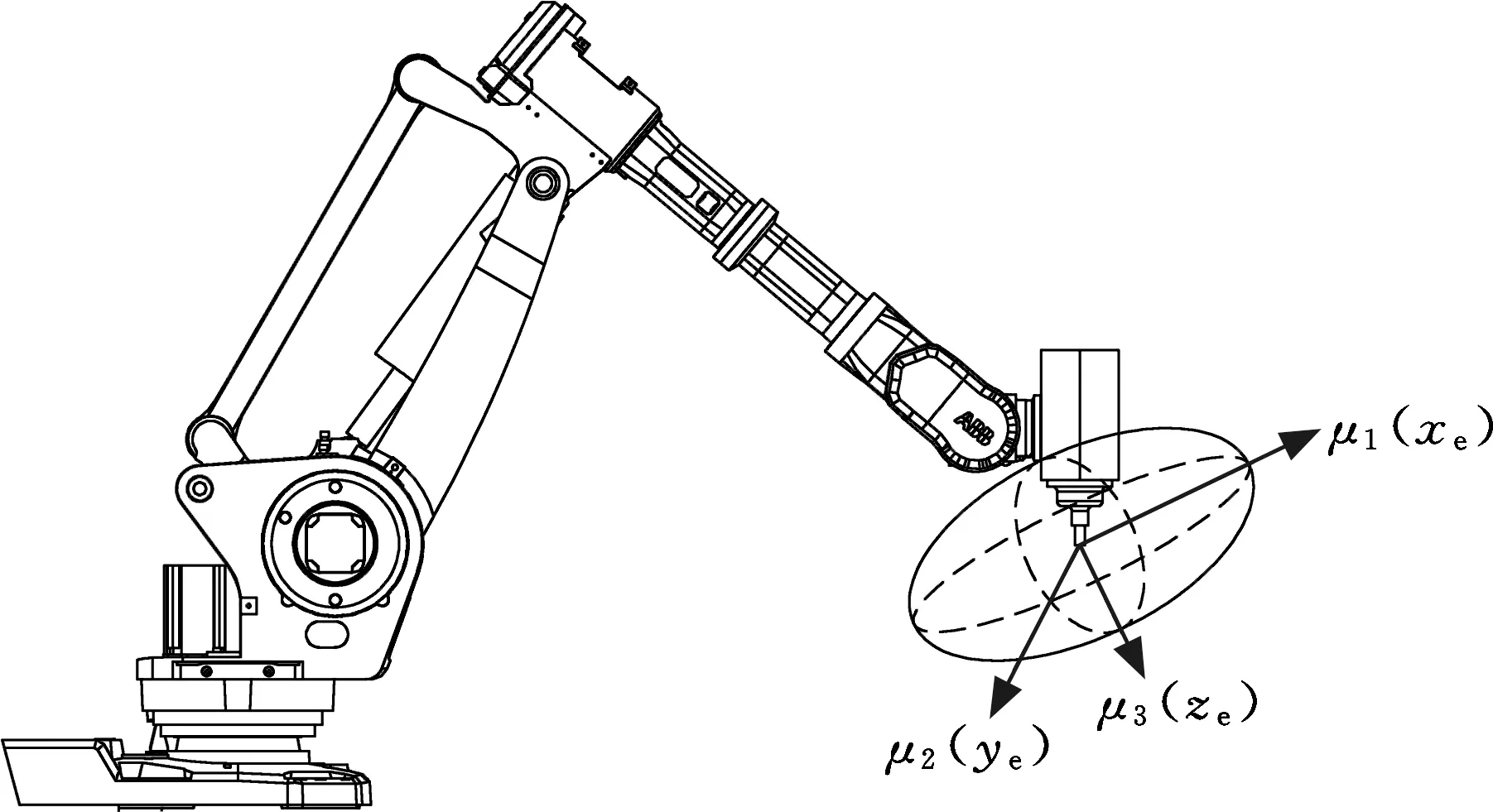
图3 机器人加工系统末端刚度椭球Fig.3 The stiffness ellipsoid of the end of roboticmachining system

该笛卡儿刚度椭球在自身坐标系{e}中的方程可表示为

(14)

椭球坐标系{e}相对于切削坐标系{c}的齐次变换矩阵Tce用刚度椭球的特征向量可表示为

(15)

式中，Rce为两坐标系的旋转矩阵。

因此，椭球面上的任意一点q在椭球坐标系中的坐标qe=(xe,ye,ze)与在切削坐标系中的坐标qc=(xc,yc,zc)满足：

(16)

式中，μij(i,j= 1, 2, 3)为特征向量μi各分量。

将式(16)代入式(14)，可得刚度椭球在切削坐标系中的方程：

(17)

则刚度椭球与切削平面的椭圆交面方程为

(18)

此时，椭圆的主轴方向即为机器人加工系统在切削平面内的主刚度方向，如图4所示，椭圆主轴方向可根据椭圆方程进一步求出。

图4 机器人加工系统主刚度方向Fig.4 The principle stiffness directions of robotic machining system

3 工业机器人铣削姿态优化算法

3.1 机器人功能冗余特性

六自由度工业机器人在铣削应用中，只需要五个自由度即可确定刀具位姿，其中三个自由度用于定位刀具中心点，另外两个自由度用于确定刀具轴线的方向，从而产生一个冗余自由度。这种特性被称为功能冗余，增加了工业机器人在执行任务时可达空间的体积和末端执行器的灵活性。如图5所示，改变机器人姿态，使得刀具坐标系{t}绕zt轴旋转角度θr，此时两个不同机器人姿态下的刀尖点位置和刀具轴向相同。这意味着对于同一加工轨迹，可以用工业机器人的不同位形进行加工，从而为优化姿态抑制模态耦合颤振提供了可能。本文用旋转角度θr表示冗余自由度，对于特定的刀具位姿，θr可以指定为在机器人可达范围内的任何值。

角度θr给定后，根据第2.1节确定的机器人D-H参数可以计算出任意加工位置处刀具坐标系相对于基坐标系的齐次变换矩阵T0t：

(19)

其中，Pi(i=x，y，z)表示刀具坐标系原点在机器人基坐标系中的位置分量。通过逆运动学求解即可推导出机器人各关节角度，从而确定各冗余角θr对应的机器人铣削姿态。

3.2 姿态优化算法

基于工业机器人功能冗余特性及所提的刚度定向方法，机器人铣削姿态优化算法如图6所示。首先，给定初始冗余角θr=0°，变化范围为0°～360°，并设定角度增量dθ。给定θr后，即可获得齐次变换矩阵T0t，通过逆运动学求解计算出机器人各关节角度；然后求取该机器人姿态下的笛卡儿空间刚度矩阵K，并推导出相应的刚度椭球，其与切削平面的交面为椭圆。通过计算该椭圆长轴及短轴方向，得到加工平面内的主刚度方向，从而确定角度α和角度γ。最后，基于模态耦合颤振稳定性判据，判断加工过程是否稳定。基本步骤总结如下：①确定初始冗余角θr，设定角增量dθ，并计算机器人各关节角度；②执行2.2节提出的刚度定向过程，得到切削平面内的主刚度方向；③根据1.2节建立的模态耦合颤振准则，判断机器人铣削的稳定性；④重复上述步骤，遍历所有θr，并检测边界，确定铣削过程稳定的机器人姿态。

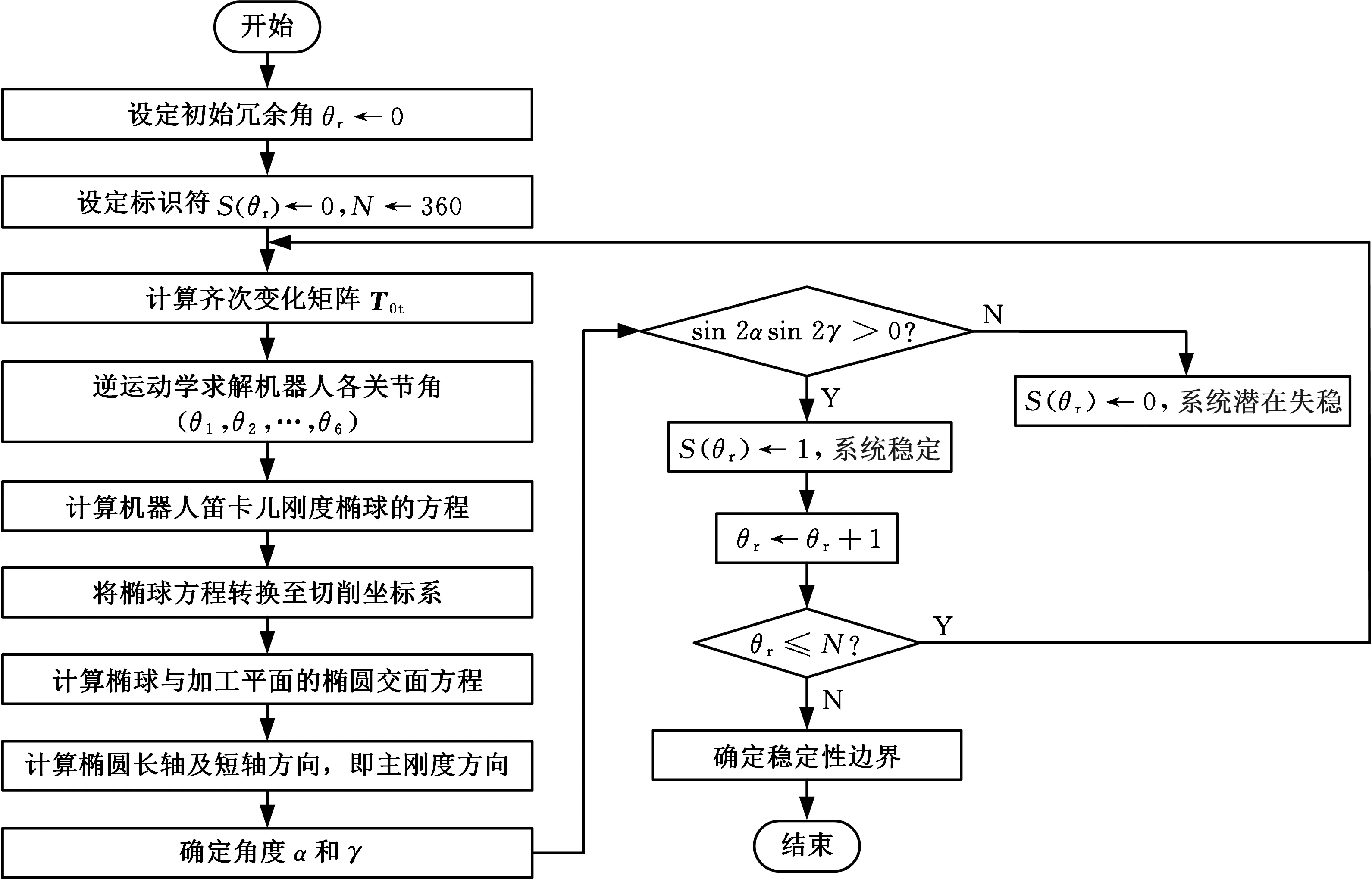
图6 机器人铣削姿态优化算法流程图Fig.6 Flowchart of posture optimization algorithm for robotic milling

4 案例分析

4.1 机器人铣削实验

实验装置如图7所示，通过将电机主轴连接到六轴工业机器人(IRB6660)的末端，搭建了机器人铣削实验平台。采用直径12 mm、螺旋角30°、刃长30 mm的硬质合金四刃立铣刀，在Q235结构钢工件(50×100 mm)上进行了平面铣削实验。通过单轴加速度传感器(3711F11100G，PCB)采集铣削过程中机器人的振动加速度信号。

为了验证利用冗余自由度优化机器人姿态避免模态耦合颤振的可行性，在两个位置分别进行半槽铣削实验和全槽铣削实验，刀尖点在两个位置处的坐标分别为(1050，-1500，875)mm、(1350，-1500，875)mm(相对于机器人基坐标系)。每组铣削实验分别在机器人12个不同位形下进行。所有实验的切削参数均为：轴向切深ap=0.3 mm，进给速度f=16 mm/s，主轴转速n=2400 r/min，铣削方式为顺铣。

图7 铣削实验装置Fig.7 Milling test equipment

4.2 结果和讨论

利用2.2节提出的刚度定向方法，计算出机器人铣削系统在位置1和位置2处不同位形下的主刚度方向。部分冗余角θr对应的机器人关节角θ1～θ6与角度α见表3。

表3 机器人关节角及主刚度方向角

根据1.2节建立的模态耦合颤振模型，位置1和位置2处的潜在颤振区域如图8中的阴影部分所示，当平均铣削力位于图8中的阴影部分时，可能发生模态耦合颤振。由式(3)和式(4)计算出半槽铣削和全槽铣削时，平均铣削力F与xc轴夹角β分别为94°和127°。将角增量dθ设定为10°，通过3.2节提出的姿态优化算法，可以判断采用不同冗余角θr对应的机器人姿态进行铣削时是否发生模态耦合颤振，预测结果如图9所示。由图9可知，机器人在位置1和位置2处进行半槽铣削时，所有位形下均不会发生模态耦合颤振；对于全槽铣削，在位置1处，冗余角θr为70°～170°时，铣削过程稳定；而在位置2处，稳定的冗余角范围扩大至0°～170°。

(a)位置1 (b)位置2图8 潜在颤振区域示意图Fig.8 Diagram of potential chatter area

图9 不同冗余角θr的稳定性预测结果Fig.9 Stability prediction respect to functional redundancy θr

为减少实验工作量，实验时设定角增量dθ=20°，采用机器人12个不同的典型位形在位置1和位置2处分别进行半槽铣削和全槽铣削实验，实验采用的冗余角如图9所示，并通过低频加速度计采集机器人振动信号。为了进一步分析实验结果，对铣削过程中的加速度信号进行快速傅里叶变换(fast fourier transform，FFT)。图10～图12所示为部分典型实验结果。

在位置1处进行全槽铣削时，为了寻找过渡冗余角边界，增加θr=70°的实验。如图10a～图10c所示，机器人在冗余角θr=0°、40°对应的位形下铣削时出现了明显的低频颤振频率(～7 Hz)，通过模态锤击实验，确定该频率接近机械臂的低阶固有频率(～7.74 Hz)，且在13个不同位形下，机械臂固有频率变化很小(7～8 Hz)；当冗余角达到70°时，7 Hz左右对应的幅值明显降低；而在冗余角θr=80°、120°、140°时，如图10d～图10f所示，7 Hz左右的颤振频率消失，说明铣削过程中没有发生模态耦合颤振，与预测结果一致。

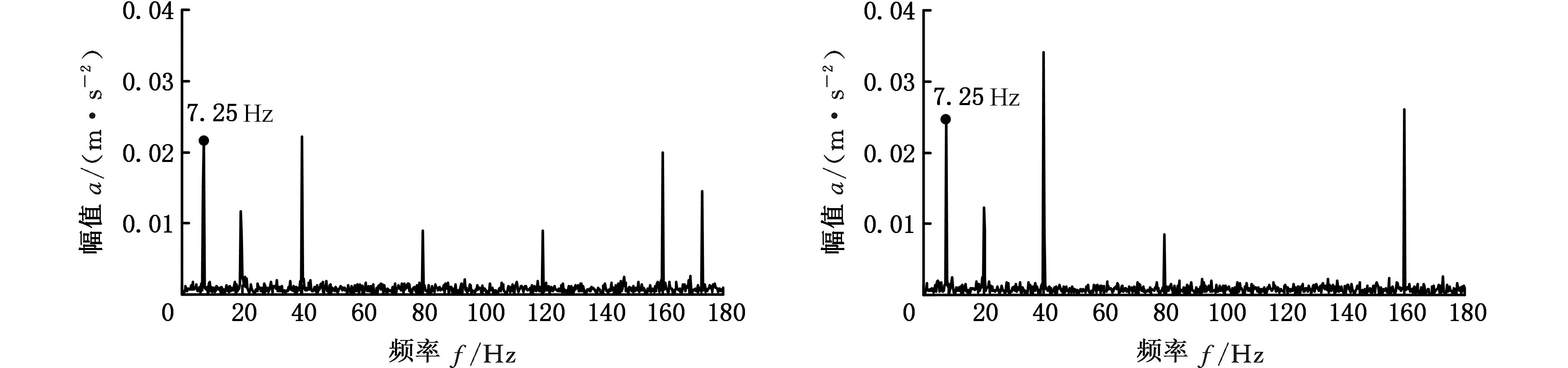
(a)θr=0° (b)θr=40°

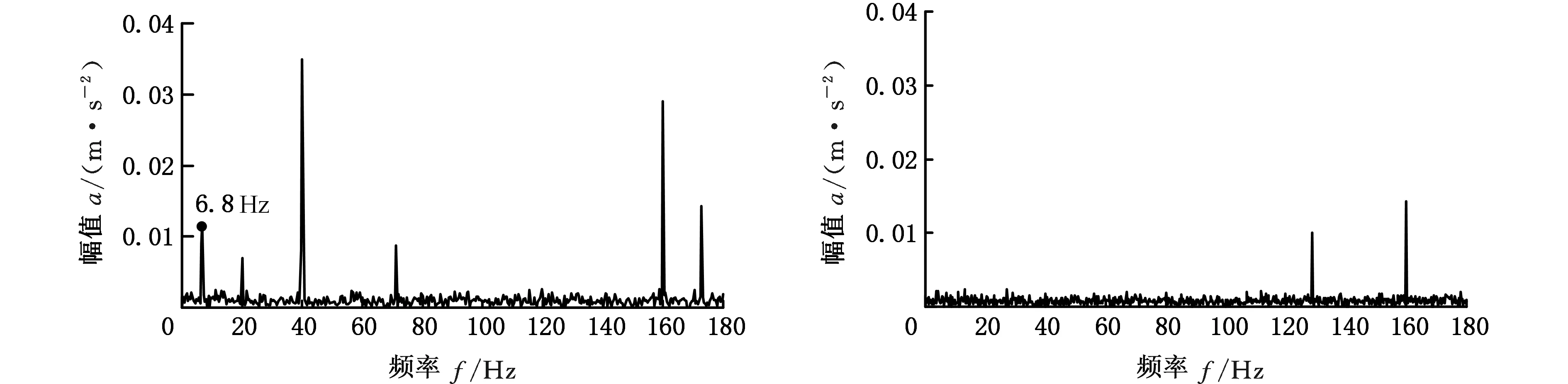
(c)θr=70° (d)θr=80°

(e)θr=120° (f)θr=140°图10 位置1处全槽铣削加速度信号频谱Fig.10 Acceleration signal spectrum of full-slot milling at position 1

在位置1处进行半槽铣削实验，实验结果显示所有冗余角下铣削过程均稳定，符合预测结果，加速度信号快速傅里叶变换的典型结果如图11所示，机器人在冗余角θr=0°、40°对应的姿态下铣削时并没有出现7 Hz左右的峰值，与全槽铣削结果对比明显，这是因为半槽铣削时，平均铣削力更加靠近y轴，从而远离了颤振区域；在位置2处进行的半槽铣削实验同样符合预测结果，在所有冗余角下均稳定。

(a)θr=0° (b)θr=40°图11 位置1处半槽铣削加速度信号频谱Fig.11 Acceleration signal spectrum of half-slot milling at position 1

位置2与位置1相比，x坐标变化0.3 m。通过模态锤击实验，12个不同位形下的机器人低阶固有频率均为8.5 Hz左右。由预测结果可知，位置2处全槽铣削时稳定的冗余角范围相比位置1扩大至0°～170°。对比表3中两个位置处的α角，位置2处各冗余角θr对应的α角的绝对值相对位置1均有所增大，这意味着位置2处的不稳定区域相比位置1逆时针旋转，如图8所示；而两个位置处平均铣削力的方向角β相同，所以位置1处不稳定的冗余角范围0°～70°在位置2处变得稳定，θr=0°、40°的实验结果如图12所示。

(a)θr=0°

(b)θr=40°图12 位置2处全槽铣削加速度信号频谱Fig.12 Acceleration signal spectrum of full-slot milling at position 2

5 结语

实验结果表明，当使用优化后的机器人姿态进行铣削时，低频模态耦合颤振被显著抑制。与以往方法不同，本文方法不需要改变刀具进给方向、工件方向或切削参数，从而保留了机器人铣削的灵活性，使得机器人加工的工业应用范围更广泛。