一种平面冗余机器人总性能最优的实时控制方法
荣 誉 豆天赐 张兴超 张 磊 赵景宇
1.燕山大学车辆与能源学院,秦皇岛,0660042.燕山大学河北省特种运载装备重点实验室,秦皇岛,0660043.河北科技师范学院机电工程学院,秦皇岛,066004
0 引言
随着电子产业的迅速发展,科技的发展日新月异,计算机类(computer)、通信类(communication)和消费类电子(consumer electronics)三类电子产品(简称“3C产品”)更新换代频繁。由于目前3C产品的装配工作大都由人工来完成,为了提高效率、降低成本,各个厂商都购买和使用现有的高速轻载机器人协助完成每个产品的装配任务,但是由于装配空间以及流水线的空间十分有限,导致人机协作的风险大大增加。目前,3C 装配领域一般采用选择顺应性装配机器手臂(selective compliance assembly robot arm, SCARA),这类机器人作为自动化生产线的辅助装备,其平面自由度仅有两个,无法完成对工作区域障碍的回避,所以其协同作业的安全性较低[1],于是将平面4R冗余度机器人引入3C产品装配的工作中,因为4R冗余度机器人拥有更多的自由度,具备更高的灵活性,能够有效降低人机协作风险,此外,还能从根源上解决能源消耗不可控的问题进而对其进行优化。
对于冗余度机器人,驱动布置是一个关乎能量消耗的问题,机器人的伺服电机通常处于关节 处,导致机器人的关节负载增大。随着机器人的发展,绳索驱动也逐渐进入大众视野,但是现阶段的绳索驱动带负载能力弱,传动效率低,应对电机实时速度方向变化的能力差。牟宗高[2]为了减小臂杆部分的质量,机械臂采用电机后置和绳索牵引的驱动方式。绳索驱动在软体机器人行业也备受关注,如JEONG等[3]采用线驱动实现各种控制算法的手康复运动可穿戴机器人;IN等[4]设计了辅助驱动器系统。
对于冗余度机器人,逆运动学求解比较困难,各国学者在冗余机械臂的逆运动学求解方面进行了大量的研究,求解方法有很多,大致分为8大类:①迭代法。以工作空间密度函数为基础的迭代算法[5]、模糊神经推理法[6]、粒子群优化求解[7]。②代数法。加权最小范数法[8]、梯度投影法[9]。③二次计算法[10]。④几何法[11-12]。⑤运动流行法[13-14]。⑥几何与数值迭代结合法[15-16]。⑦倍四元数法[17]。⑧退化自由度法[18]。上述方法均有优缺点,例如:迭代法需要的算力很大,耗费时间长;几何法具有求解快、精度高的优点,但是通用性较差[19]。
冗余度机器人可以改变位姿,完成优化的轨迹,以此达到最优控制。ROUT等[20]提出了教与学优化算法(teaching-learning-based optimization, TLBO)对目标函数进行寻优。HUANG等[21]选择NSGA-Ⅱ算法对时间和平均冲击目标寻优求解。沈悦等[22]采用加权系数法将时间和二次多项式双目标变为单目标。SERRALHEIRO等[23]引入惩罚系数来建立时间和能耗的多目标优化。徐海黎等[24]采用弹性系数和加权系数法定义时间与能耗的目标函数。MULIK[25]同时考虑时间、能耗和冲击等五个指标。施祥玲等[26]引入权重系数分配法建立时间、能耗和冲击组成的总目标模型。邓乾旺等[27]提出应用蜜蜂进行型遗传算法求解最优能耗轨迹。
对于冗余度机器人,动力学建模是后续优化的基础,也是控制的前提。常见的动力学建模方法有:①牛顿-欧拉方法[28];②拉格朗日方程法[29];③凯恩方法[30];④罗伯特-维登伯格方法[31];⑤高斯最小约束原理方法[32]。其中,牛顿-欧拉方法和拉格朗日方程法使用更为广泛。由于拉格朗日方程法对系统整体进行动力学建模,更加简单和方便,故本文采用拉格朗日方程法。
本文从提高整体性能方面出发,在结构设计上受绳索驱动的启发,提出了以同步带为传动方式的驱动集中布置的方案,此方案可使机器人关节负载降低,提高带负载能力、传动效率以及应对实时速度方向变化的能力。本文在冗余度逆运动学求解的基础上,基于加权M-P伪逆法提出了一种预设空间降维法,通过优化项来确定运动学逆解从而得到路径插值点所对应的各个关节角度。此方法可有效地对负载大杆件进行角度分配以及全局角度摆动幅度的调控。建立机器人动力学模型,得到各个关节驱动力矩用于后续优化处理,由前文可知,国内外研究人员采用的各种优化方法非常丰富,优化目标也都相对完善,但是针对总能量、总力矩和总时间的综合优化却报道较少。随着智能优化算法的兴起,粒子群算法脱颖而出,该算法因实现容易、精度高、收敛快的优点而被广泛使用。随着时间的缩短,以动能为指标的能量消耗必然增加,总力矩也会增大,会造成性能不均衡,关节磨损加剧,缩短使用寿命。本文将总能量消耗最优、总力矩最小和时间相对最短三个指标通过加权系数整合为综合指标,以综合指标作为目标函数,采用粒子群优化算法对时间进行寻优,最后通过仿真及样机验证来检验该算法的有效性。
1 结构设计
传统SCARA类机器人平面自由度仅有两个,协同作业的安全性较低,而且此类机器人的驱动单元都布置在关节处,所以其高速运动时的转动惯量偏大[33]。本文设计的平面冗余度机器人采用驱动集中后置布置的形式,各个关节均为转动副连接。驱动动力通过同步带和同步带轮来完成传输。由于驱动集中后置布置,故各个关节的负载大大减小,减小了机器人在高速运动时的转动惯量,进一步提高了作业效率,并且能使整个系统更加平稳,因本机器人拥有两个冗余自由度,故其能够更好地辅助人完成工作。机器人模型如图1所示。

1.伺服电机 2.行星减速机 3.轴一 4.杆一 5.轴二 6.杆二 7.轴三 8.杆三 9.轴四 10.杆四 11.小带轮 12.大带轮 13.长同步带 14.电机连接板 15.短同步带 16.加强筋 17.墙板图1 4R冗余机器人三维图Fig.1 3D diagram of 4R redundant robot
2 冗余度机器人运动学建模
2.1 机器人运动学建模
本文采用齐次变换方法,该方法通用性极强,并且能够将运动控制算法、动力学、矩阵运算及变换及几何关系映射等联系起来,方便理解和使用。
运动学分析主要包含两个部分:运动学正解及运动学反解。正运动学求解是指已知机械臂的臂形参数以及各个关节转动的角度以此求取末端操作器的状态变量,正运动学存在唯一解;运动学反解是指已知末端操作器的状态变量,求取各个关节状态,对于冗余度机械臂,逆解存在多组解,因此,需要一种特定的求解算法。
2.2 机器人D-H坐标的建立
在笛卡儿坐标系中根据D-H参数法对图1所示机器人建立各连杆坐标系,并设定各个连杆的参数。图2所示为机械臂各个关节坐标系定义,可以看出4个连杆相互之间的串联关系以及坐标系定义规则。平面4R冗余机器人的D-H参数见表1,其中,αi为连杆转角;ai为连杆长度;di为连杆偏距;θi为关节角。

图2 平面4R冗余机器人D-H坐标系Fig.2 D-H coordinate system for planar 4R redundant robot

表1 4R冗余机器人D-H连杆参数
2.3 机器人正运动学建模
已知机器人的几何参数及关节角矢量,需求解末端执行器相对于固定基座的位姿,即齐次变换问题。采用坐标变换方法表示从坐标系{0}到坐标系{i}的变换过程,连杆变换矩阵公式为
rot(X,αi)trans(X,αi)rot(Z,θi)trans(Z,di)=
(1)

(2)
nx=oy=cijkmny=-ox=sijkm
nz=oz=ax=ay=pz=0az=1
cijkm=cos(θi+θj+θk+θm)
sijkm=sin(θi+θj+θk+θm)
由式(2)可知,冗余度机器人末端位置为
(3)
2.4 冗余机器人逆运动学分析
冗余度机器人末端的速度即操作速度为
(4)
关节空间下的速度为
(5)
用雅可比矩阵将关节速度与操作器末端的笛卡儿速度联系起来,则有以下关系:

(6)


图3 冗余度机器人雅可比矩阵J的子空间示意图Fig.3 Redundancy robot jacobian matrix J subspace schematic diagram
(7)
则有
(8)
因此,可得
(9)
本文通过对瞬时关节最优速度求解,将末端实际位置与现在位置进行对比,然后将位置差作为实际位置和现在位置的步长,通过雅可比伪逆与每个步长距离相乘得出角速度,将此角速度与时间插值相乘得到关节角增量,再与原有角度相加从而得到关节角度,以下为具体分析方法。
(10)
针对该冗余度机器人雅可比矩阵J(q)为2×4长方阵,其逆矩阵不存在,所以引入雅可比矩阵的伪逆矩阵来进行求解。伪逆具体形式为
J(q)+=J(q)T(J(q)J(q)T)-1
(11)
冗余自由度机器人速度方面的解已经有了很大的突破,其中具有加权M-P逆解具有各关节同步运动、无关节自运动的特点[34],本文采用梯度投影法和此方法相结合,对于四轴串联机器人系统,以总摆动幅度最小作为原则,为各个轴分配转动权值,从而建立权值向量:
W=[W1W2W3W4]T
(12)
故此时的伪逆具体形式为
J(q)+=W-1J(q)T(J(q)W-1J(q)T)-1
(13)
由此得到该冗余度机器人关节速度:
(14)
当J(q)+满秩时,满足以下条件:
(15)

表2 加权矩阵主对角元素与角度幅度关系
由于冗余度机器人的逆运动学的解具有非唯一性,故以总摆动幅度最小作为优化项来选择冗余度机器人逆解。在表2中发现[1 100 1 1]这一组加权值更加符合条件,本文通过算法实现以及大量实验验证,即使此时100加大到10 000或减小一部分对结果影响也不大,为了方便计算和记录,故选取[1 100 1 1]这组策略,可以看到关节2的转动速度很小,几乎不动,而关节1、关节3和关节4对末端速度贡献更大,相当于四杆变三杆。此为预设空间降维法的核心部分。此方法将在之后机械臂关节故障下重新建模与容错控制研究方面起到重大作用。
2.5 基于三次多项式的轨迹生成
在轨迹规划过程中,主要是求出多项式系数,随着多项式次数增加,计算量也会随之增大,要求我们根据不同的情况选取合适的多项式。在相对满足规划要求的情况下,选择计算量相对小的多项式,可以提高控制反馈误差,故本文采用三次多项式插值规划轨迹。
在规划轨迹的过程中,需要知道以下参数:①始末两点的角度;②始末两点的速度。 插值点初始速度为零,末端速度也为零,其他点归为起始点和终止点,但是速度不为零,利用前一段轨迹终端速度和加速度作为下一段轨迹起始速度和加速度,可以得到由三次多项式构成的轨迹。θ0为起始点关节角,θf为终止点关节角。设三次多项式函数表达式为
θ(t)=a0+a1t+a2t2+a3t3
(16)
起始和终止点位置约束为
(17)
起始速度约束为
(18)
速度和加速度用三次多项式可分别表示为
(19)
解方程组可得三次多项式的系数分别为
(20)
由此可知,三次多项式和轨迹终止时间存在函数关系,因此,可以找到一个时间,使得这一段轨迹内综合性能最优。
3 冗余度机器人动力学建模及优化
3.1 拉格朗日动力学建模
拉格朗日方程是以能量守恒为基础的研究机械臂动力学的一种常用方法。运用拉格朗日法建立动力学方程的核心是确定系统的动能关系,拉格朗日函数用L表示,其函数表达式如下:

(21)
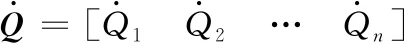
以机械臂的第i个连杆为例,其动能是由连杆质心的线速度和角速度共同作用产生的,用Ki表示,其数学表达式如下:
(22)
其中,mi为连杆i的质量;vci为该连杆的线速度;ωi为该连杆的角速度;Ii为该连杆的惯性量。则机械臂的总动能等于组成该机械臂n个连杆动能之和:
(23)
对于机械臂的第i个连杆,其势能用Pi表示,其数学表达式如下:
Pi=-migTPci
(24)
其中,g表示该连杆的重力加速度矢量;Pci表示该连杆质心在坐标系中的位置矢量。则机械臂的总势能就等于组成它的n个连杆的势能之和:
(25)
机械臂的拉格朗日方程表达式为
(26)
其中,τi表示第i关节的驱动力或者力矩,i=1,2,…,n,由于此处关节是转动关节,故τi表示第i关节的驱动力矩。以机械臂的第i连杆为例,运用拉格朗日方程进行推导,根据机械臂的功能关系可以很明确地建立其动力学方程,在推导的过程中可以完全忽略连杆之间不做功的约束反力及摩擦力等,思路清晰,并且简化了推导过程,所以,相对于牛顿-欧拉方程和凯恩方程,拉格朗日方程对建立机械臂的动力学方程更具有优势。
3.2 冗余机器人动力学方程的建立
根据上文运用拉格朗日方程建立机械臂动力学推导过程,总结为以下步骤:①通过上述分析运动学所建立的坐标系,确定独立的广义关节变量qi,i=1,2,…,n;②确定机械臂相应关节上的广义力Fi;③求解机械臂各个关节的动能和势能,构建拉格朗日函数;④代入拉格朗日方程,建立机械臂动力学方程。
针对平面冗余4R机器人,应用上述由D-H建立的连杆坐标,可以得到各个连杆质心在基坐标系中的表示:
(27)
由于该机械臂的作用平面在同一水平面上,故此时的重力势能为0。通过上述给定的拉格朗日函数公式,L定义为机械系统的总动能K减去总势能P,即
L=K-P
(28)
则可得到系统的动力学表达式:
(29)

由于势能与速度是无关的,故动力学方程可写成
(30)
最后整理动力学方程如下:

(31)
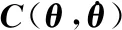
4 多目标综合性能优化
上文利用三次多项式构造了空间机械臂的关节轨迹,下面建立多目标规划问题的数学模型。
4.1 目标函数
本文研究平面冗余度机器人的4个关节,由于三次多项式的系数和结束时间有关,故定义如下3个优化目标:
(32)
(33)
S3=tf
(34)
式中,tf为机械臂总时间;τ为机械臂力矩;EK为机械臂能量。
以上3个优化目标中,S1为关节的总能量,可以作为衡量机械臂关节的能量消耗的指标;S2为关节的总力矩,可以作为衡量关节磨损的指标;S3为机械臂运动时间,可以作为衡量机械臂运动效率的指标。
设定运动学、动力学和时间约束条件,将机器人多目标综合最优问题表达如下:
(35)
4.2 基于粒子群算法的多目标优化问题求解
单一指标的优化已经难以满足现代工业的生产需求,所以多指标综合性能优化拥有很大的研究价值。由式(35)可知,若想达到综合最优,其中唯一的变量为结束时间,各指标相互对抗,S1、S2越小越好,而S3(时间)则是在一定范围内,若其偏小,速度和加速度会偏大,机械臂运动不平稳,反之则效率不高。采用加权系数将多指标变为综合指标,以综合指标作为目标函数然后采用粒子群优化算法对时间进行优化。粒子群优化算法的计算步骤如下:
(1)随机初始化n个粒子的位置和速度,计算每个粒子对应的适应度,确定个体最优值p_best和种群最优值g_best,令k←0。
(2)判断收敛条件是否满足,若满足,则停止搜索,输出最优结果X*=g_best;否则,转到下一步。
(3)更新所有粒子的位置及速度,并计算各粒子的适应度,更新p_best、g_best,令k←k+1。
(4)转到第(2)步,直至收敛。
4.3 粒子群算法与其他算法的对比
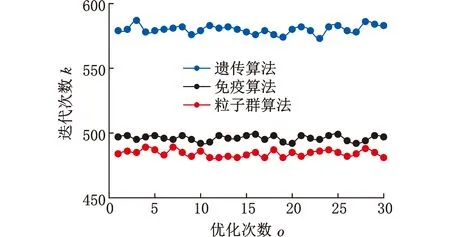
对5种不同类型的函数分别用遗传算法、免疫算法和粒子群算法进行优化,如图4所示。可以看到,遗传算法显得有些吃力,免疫算法和粒子群算法旗鼓相当,但是观察图4b可以明显发现,免疫算法的迭代次数居然超出了遗传算法的迭代次数,说明该算法针对不同函数时,其稳定性也不尽相同,而粒子群优化算法的迭代次数始终保持在较低水平。

(a)函数一

(b)函数二

(c)函数三
(d)函数四

(e)函数五图4 不同函数下不同算法性能对比Fig.4 Performance comparison of different algorithms under different functions
各算法针对不同函数的平均迭代次数见表3。由上述数据分析可知,粒子群算法更加有效且收敛速度更快,稳定性更好,故本文采用粒子群优化方法对函数进行优化。

表3 各算法针对不同函数的平均迭代次数
4.4 粒子群算法的应用
本文对多目标进行综合优化,将每个目标与权重系数相乘再相加得到的值作为目标函数,将结束时间作为变量,满足目标函数值最小的结束时间即为本文寻优的值。
按照粒子群算法对初始值进行5次优化,a、b、c分别为加权参数,其作用是保证三个指标相对协调即归一化处理,并且进行加权起到了强调某项指标在整体中的重要程度,本文取a=b=1/107,c=8。优化结果保留4位小数,具体优化结果见表4。

表4 粒子群优化结果
5 实验验证
本文基于综合性能最优,结合实践考虑,选择最优的数据进行实验验证,在轨迹规划中对路径点进行插值,然后点和点之间再进行关节空间规划,故只需求点和点之间最优即可。
本实验以直线为优化轨迹,选择总关节幅度相对较小的加权矩阵,通过逆解得到关节位置,进而对该机械臂所完成时间进行优化。实验样机的搭建如图5所示。

图5 实验样机搭建Fig.5 Experimental prototype construction
以总幅度相对较小作为标准,图6为跟踪直线轨迹的机械臂形态图。

图6 冗余机器人状态Fig.6 Redundant robot state diagram
机械臂状态仿真如图7所示,可知样机的动作和仿真形一致,关节摆动角度总幅度相对较小,证明了本文提出的预设空间降维法是正确的。

图7 冗余机器人状态仿真Fig.7 Redundant robot state simulation diagram
图8为优化前后能量对比图,可以明显看出优化前后峰值的变化。图9为优化前后总能量扇形对比图,可以明显看出优化量占总能量的百分比。图10为优化前后力矩对比图,可明显看出优化前后峰值的变化。图11为优化前后总力矩对比图,可明显看出优化量占总能量的百分比。

图8 优化前后能量对比Fig.8 Comparison of energy before and after optimization

图9 优化前后总能量对比Fig.9 Comparison of total energy before and after optimization

图10 优化前后力矩对比Fig.10 Comparison of the torque before and after optimization

图11 优化前后总力矩对比Fig.11 Comparison of the total torque before and after optimization
图12为整体性能优化前后对比图,可以看出整体性能优化了1.9%。图13为优化前后各指标对比图,可以看出总能量优化了17.65%,总力矩优化了17.83%。

图12 优化前后总性能对比Fig.12 Total performance before and after optimization

图13 优化前后指标对比Fig.13 Comparison of indexes before and after optimization
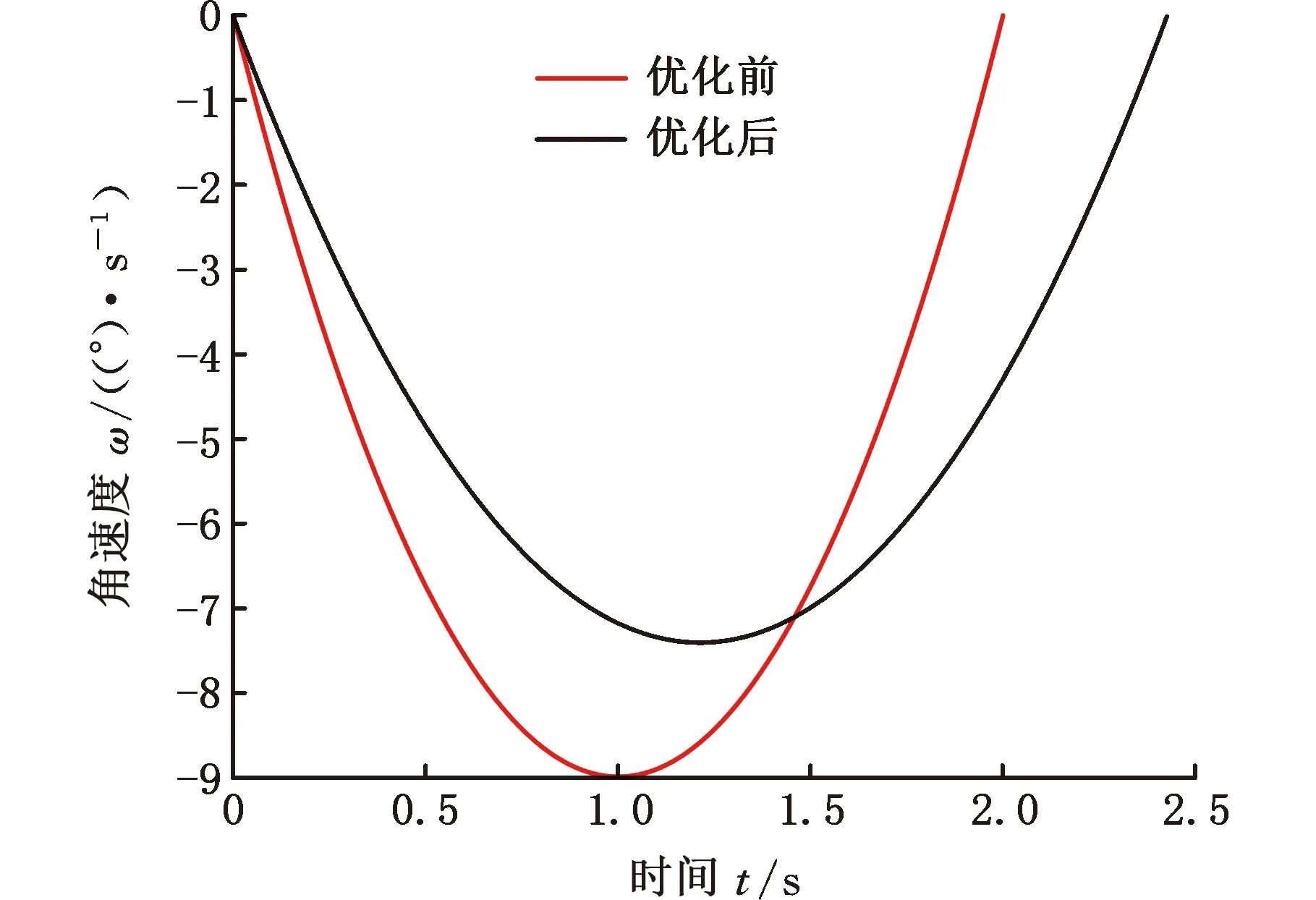
图14所示为各关节优化前后各角度与时间关系变化。图15所示为各关节优化前后各关节速度与时间关系变化。图16所示为各关节优化前后关节加速度与时间关系变化。图17所示为各关节优化前后力矩与时间关系变化。经过计算机仿真和实物验证,发现优化总能量S1、总力矩S2和总时间S3之后,机械臂的其他性能也有所提高。由图14可知,优化后的各个关节角度与时间的关系更加平缓,性能更加稳定。由图15 可知,优化后的各个关节速度峰值降低,增加了协作的安全性。由图16可知,优化后各个关节加速度变化幅度更小。由图17可知优化后各个关节的力矩明显降低,延长了电机的使用寿命。
6 结论
本文以平面冗余度机器人为研究对象,提出了驱动集中布置的方案,此方案提高了作业效率并且使工作时更加平稳。对路径点进行插值,以总摆动幅度作为优化项目,然后通过基于加权M-P伪逆的预设空间降维法进行逆运动学求解。以总能量、总力矩及总时间为目标函数,采用粒子群优化以综合指标为目标函数对结束时间寻优。通过实验以及仿真验证,得到优化前后的对比图,直观表现出优化前后的数值,在优化综合指标的同时,机械臂其他性能也得以提高。由对比图可知本文方法真实可行。

(a)杆一

(b)杆二

(c)杆三

(d)杆四图14 优化前后各杆角度随时间变化对比Fig.14 Comparison of angle of four front and rear bars changing with time before and after optimize
(a)杆一

(b)杆二
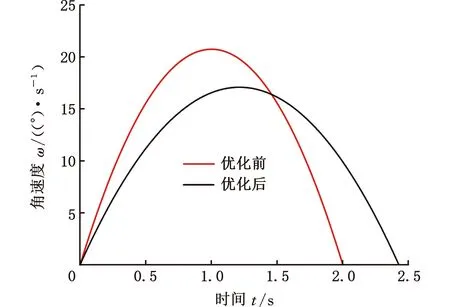
(c)杆三

(d)杆四图15 优化前后各杆角速度随时间变化对比Fig.15 Comparison of velocity of four front and rear rod corner changing with time before and after optimize

(a)杆一

(b)杆二

(c)杆三

(d)杆四图16 优化前后各杆角加速度随时间变化对比Fig.16 Comparison of angular acceleration of four front and rear rods changing with time before and after optimize

(a)杆一

(b)杆二

(c)杆三

(d)杆四图17 优化前后各杆驱动力矩随时间变化对比Fig.17 Comparison of driving torque of four front and rear rods changing with time before and after optimize

