裂纹故障对轮齿时变啮合刚度的影响分析

孟 宗 李佳松 潘作舟 庞修身 崔玲丽 樊凤杰

1.燕山大学电气工程学院，秦皇岛，0660042.北京工业大学机械工程与应用电子技术学院，100124

0 引言

齿轮传动系统在工业领域应用范围极为广泛[1],与人类生产生活息息相关。齿轮作为旋转机械中改变转速与传递扭矩的重要零部件之一，长期处于复杂、变化环境下，易产生磨损、裂纹、点蚀、剥落、断齿等故障[2]。裂纹作为齿轮故障主要存在形式之一，产生的危害轻则影响设备正常工作，降低人类生产效益，重则威胁人类生产生活安全，甚至造成机毁人亡惨剧，因此，对齿轮传动系统进行故障检测与健康监测具有重要意义。齿轮振动来源于系统内部激励与外部激励，刚度激励作为内部激励的主要来源，当齿轮啮合时，裂纹使齿轮时变啮合刚度(time-varying mesh stiffness,TVMS)发生不规则变化，进而引起齿轮异常振动，产生较大噪声，因此，准确计算TVMS是构建动力学模型的关键所在。针对裂纹故障情况下的齿轮TVMS的计算及动力学分析，国内外学者做了许多研究。万志国等[3]考虑齿根圆与基圆大小不重合现象，对TVMS算法进行改进，并与ISO标准比对，结果表明误差在5%以内。张振等[4]提出双齿根裂纹模型，指出在两轮齿裂纹深度之和相等的前提下，具有最大裂纹深度模型对TVMS劣化率有较大影响。YANG等[5]构建了考虑齿廓间隙与轴承间隙的四自由度动力学参数模型，研究了不同故障程度下齿轮系统的动力学响应，结果表明故障程度越高，系统庞加莱截面图与相图越混乱。李秀红等[6]通过ABAQUS确定裂纹萌生位置，分析影响齿轮疲劳寿命的多种因素，最终选取合适齿顶修缘量与增大表面硬化方法来延长齿轮使用寿命。MA等[7]考虑了裂纹分别沿基体和轮齿拓展的两种情况，并根据有限元法得出裂纹在相同深度情况下，对沿基体方向拓展的TVMS影响最大的结论。CHEN等[8]采用解析有限元法对复杂基体类型的TVMS进行求解，结果表明与轮缘厚度相比，腹板厚度对TVMS的影响更大。吴家腾等[9]通过实验台采集裂纹轮齿的齿根应变，将其与有限元法计算得到的应变代入反问题模型中，实现了对TVMS的反向求解。MENG等[10]采用两种方法计算了在不同裂纹等级下振动信号的统计指标，结果表明峭度指标对早期故障特征较为敏感。雷敦财等[11]参照圆柱直齿轮有限元模型构建方法，得出面齿轮传动载荷分布不均匀、TVMS呈周期性正弦曲线变化的结论。

作为TVMS的两种基本计算方法，有限元法与解析法各有利弊。有限元法是将齿轮模型离散为若干微小单元，并通过施加相应载荷条件与边界条件计算系统各部分发生的位移；解析法则是在MATLAB中构建TVMS参数模型并输入相应齿轮参数进行求解计算。相比有限元法，解析法求解速度较快但精度较差。因此，通过研究TVMS的变化规律并对模型算法进行合理改进，可以保证解析法运算效率以及结果的准确性。

本文首先修正了双齿啮合区TVMS计算公式，减小了计算误差；其次，分析“死区”的产生原因，通过有限元法确定轮齿易发生断裂的位置；构建了分别沿裂纹深度与长度方向的拓展曲线，定量研究了不同裂纹深度及长度对TVMS的影响规律；最后讨论了不同裂纹深度下的轮齿对承载能力的变化过程。

1 健康齿轮TVMS计算

齿轮在正常工况下工作时，轮齿接触数量与啮合位置发生周期性改变，并使TVMS呈现周期性(高-低-高)变化规律[12]。在单双齿交替时刻，刚度发生突变产生啮合冲击并导致振动幅值改变。因此，准确评估TVMS有助于描述齿轮传动系统动态响应，为动力学参数模型的确立提供必要条件。

1.1 轮齿齿廓方程的确定

根据材料力学相关理论，将圆柱直齿轮轮齿简化为固定在齿根圆上截面不断变化的悬臂梁。轮齿齿廓共由三部分组成，如图1所示，分别为齿顶圆圆弧(AB段)、渐开线齿廓(BC段)和基圆与齿根圆之间的过渡曲线(CD段)[13]，轮齿齿廓沿x轴对称分布，在BC段上轮齿相互接触并发生啮合过程，BC段渐开线曲线公式为

x=Rb[sin(α2+α)+cosα]

(1)

hx1=Rb[cos(α2+α)-sinα]

(2)

图1 健康轮齿悬臂梁Fig.1 Healthy tooth cantilever beam

过渡曲线虽未因接触发生形变，但对分析轮齿弯曲形变有重要意义。近年来，诸多学者将过渡曲线简化为一条直线[14]，但实际加工采用展成法切削方式，渐开线与过渡曲线分别由标准齿条的直线部分与齿顶圆弧部分切割而成，过渡曲线表达式为

(3)

(4)

(5)

式中，r为分度圆半径；a1为齿顶圆弧圆心距中线距离；rρ为齿顶圆弧半径；b1为齿顶圆弧圆心距齿条齿槽中心线的距离；γ为变参数，变化范围为α0≤γ≤π/2；α0为分度圆压力角。

1.2 改进势能法计算公式

TVMS作为表征振动特性的一个重要指标，具有重要研究价值。根据弹性力学相关理论，接触齿对所具备的总势能U包括轮齿具有的势能Utooth与轮体具有的势能Ubody，Utooth包括赫兹接触势能Uh、弯曲势能Ub、剪切势能Us、轴向压缩势能Ua。根据势能与刚度的对应关系，可推导出赫兹接触刚度Kh、弯曲刚度Kb、剪切刚度Ks、轴向压缩刚度Ka及基体刚度Kf。随着齿轮转动，啮合点沿着发生线移动，产生不同变形量，引起势能与刚度改变，其中，总势能及每部分刚度计算公式为

(6)

(7)

(8)

(9)

(10)

(11)

(12)

式中，F为啮合力；E为弹性模量；L为齿轮宽度；μ为泊松比；d为啮合点到齿根圆距离；h为啮合点距轮齿中心线高度；G为剪切模量；hx1、hx2分别为距离齿根圆x处且分别位于渐开线与过渡曲线处的齿廓与x轴的距离；Ix、Ax分别为距离齿根圆x处的截面惯性矩与截面面积。

计算基体变形量时，假设轮齿是刚性的，而轮体为一个弹性圆环，当齿对参与啮合时，认为轮齿不会因接触而变形，但会导致齿轮体产生弹性形变，进而引起轮齿发生形变。在双齿啮合区，当同时有第i与第j对(i≠j)轮齿参与啮合过程时，传统方法仅考虑第i(j)对齿的啮合力在轮体作用下对第i(j)对齿沿发生线的变形量，却忽视第i(j)对齿的啮合力对第j(i)对齿的变形量。因此，低估由轮体偏转作用下引起的轮齿总变形量，从而高估双齿啮合区TVMS数值，这种不同齿对之间的变形量互相影响的现象称为相邻齿耦合效应。MA等[15]通过有限元法确定修正系数并对双齿啮合区的基体刚度进行修正。随后XIE等[16]基于弹性圆环理论，假设在齿根圆处法向应力呈三次分布、切向应力呈抛物线分布，并对基体刚度进行改进。相邻轮齿耦合效应示意图见图2a，轮齿i与轮齿j在耦合效应作用下的变形量计算公式分别为

(13)

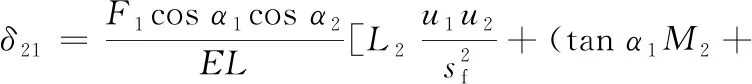
(14)

其中，δij(i≠j)为考虑相邻齿耦合效应时，当第j个轮齿在啮合变形时对第i个轮齿沿发生线造成的变形量；Fi、ui、αi定义方式如图2b所示，i表示轮齿编号。Ai～Ii数值参考文献[16]，参数Mi、Qi、Ti、Ui与Li、Pi、Ri、Si、Vi计算公式如下：

(15)

(16)

(a)相邻齿耦合效应示意图(b)轮齿受力放大图图2 相邻齿耦合效应Fig.2 Coupling effect of adjacent teeth

在双齿啮合区，除了考虑由相邻齿耦合效应引起的齿形变外，仍需考虑啮合齿对i(j)受轮体弹性形变作用产生的变形量的影响，在两者共同影响下引起基体变形，总的基体变形量公式为

δf1=F1δ11+F2δ12

(17)

δf2=F1δ21+F2δ22

(18)

(19)

(20)

(21)

则单、双齿啮合区TVMS的计算公式分别为

(22)

(23)

其中，δf1、δf2为在不考虑齿接触变形时，轮齿沿啮合线的总变形量；δij(i=j)为当第j个轮齿在啮合变形时对第i个轮齿沿发生线造成的变形量；Lsr1、Lsr2为齿对负载分担比。上标和下标p、g分别代表主、从动轮，i代表接触齿对的数量，采用表1所示的齿轮参数，将基于改进势能法的TVMS结果与其他方法进行对比，如图3所示。

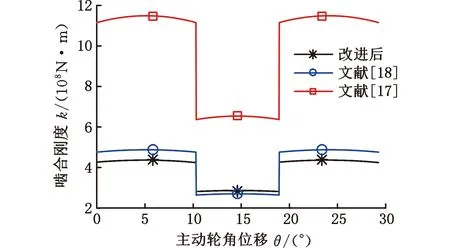
图3 不同方法TVMS对比Fig.3 TVMS Comparison of different methods

由图3可以看出，文献[17]与其他两种方法相比，在单双齿啮合区TVMS均相差过大，这是由于该方法视齿轮体为刚性，只考虑轮齿的形变作用，而忽略了轮体变形量的影响，使得TVMS计算结果过大。文献[18]为传统势能法，与改进后势能法相比结果相差不大，但在双齿啮合区未考虑由相邻齿耦合效应引起的轮齿变形量，使得整体变形量偏小，而在单齿啮合区由于齿轮变形量拟合方程系数差异性引起结果不同。因此，改进后势能法与另外两种方法相比，考虑范围更为全面，能够得到更准确的齿轮变形量，获得更精确的TVMS数值。

2 裂纹齿轮TVMS计算

TVMS异常变化是齿轮故障及外界工况变化等诸多因素共同作用的结果。当旋转机械长期在高强度的环境下工作时，在齿根附近会产生应力集中现象并生成微观裂纹。随着循环加载次数累积，形成宏观裂纹并逐步传播，从而导致TVMS随之下降，使得振动信号故障特征愈发明显，因此由裂纹故障引起的危害是不容忽视的问题。本节考虑裂纹在不同时期拓展情况，构建不同裂纹模型并分析不同裂纹深度与长度对TVMS的影响。

2.1 沿深度方向拓展裂纹模型的构建及TVMS计算

与健康轮齿相比，裂纹导致轮齿截面面积A(x)及截面惯性矩I(x)减小，其原因为在载荷作用下，这部分轮齿缺乏足够机械强度，被称为“死区”，表明该部分轮齿不但失去正常承载能力，而且会在弯曲应力持续作用下拓展范围越来越大，直至产生断齿故障并导致轮齿对的承载能力完全丧失。根据第一强度理论，最大拉应力为引起材料断裂的最主要因素，以此为依据可确定裂纹萌生位置。文献[19]指出裂纹萌生点位于渐开线齿廓上，结合文献[20]的分析方法，在ANSYS Workbench静力学模块中，对单齿啮合区一点施加500 N的载荷，并约束轮孔表面的6个自由度，主应力分析结果如图4所示。结果表明齿轮最大拉应力点位于过渡曲线处(图4中红色区域)，而不是在渐开线齿廓上，因此，可确定裂纹萌生点多发生在过渡曲线附近[20]。

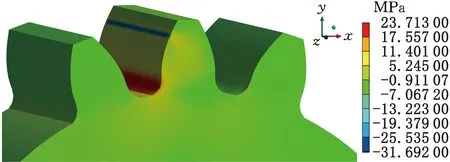
图4 最大主应力分析结果Fig.4 Analysis results of maximum principal stress

在裂纹拓展相关研究中，多数情况将裂纹简化为对称直线，但由于裂纹拓展到轮齿对称线时，拓展速度加快、斜率更大，故将下半部分裂纹形状修正为斜率更大的圆弧。如图5所示，q1为未穿过x轴裂纹深度，此时裂纹尖端位于E点；随着故障程度加剧，裂纹深度到达x轴(G点)并穿过x轴到达H点处，将穿过x轴裂纹深度记为q2，这两部分深度之和记为总裂纹深度q。本文中，裂纹拓展角度取常数θ=80°，研究裂纹是否穿过x轴两种情形，A(x)与I(x)计算公式如下。

图5 裂纹轮齿悬臂梁Fig.5 Crack tooth cantilever beam

情形1：当裂纹深度在x轴上方，如图5中E点所示，即裂纹总深度q≤q1max且q≥0时，有

(24)

(25)

hc=q1/sinθ

(26)

情形2：当裂纹深度在x轴下方，如图5中H点所示，即裂纹总深度q=q1max+q2>q1max时，有

A(x)=

(27)

I(x)=

(28)

(29)

(30)

由式(24)～式(30)可知，在由齿根圆向齿顶圆啮合过程中，情形1与情形2均会导致A(x)与I(x)减小。为更直观地分析轮齿在不同裂纹深度下TVMS的变化规律，将裂纹深度取整，数值分别为0、1 mm、2 mm、3mm，且每种深度都有相应故障程度并对应表2，TVMS变化结果如图6所示。

表2 裂纹深度参数

由图6看出，裂纹使单双齿啮合区TVMS结果发生改变，当裂纹深度较小时，TVMS减小但变化不明显，且随着深度增加降幅逐渐变大。在第一个双齿啮合区比第二个双齿啮合区降幅要小，这是由于在初始啮合阶段健康齿对起主导作用。同时，负载分担比作为衡量齿对承载能力变化的一个重要指标，能够更加直观地描述齿对在不同故障程度下承载能力的变化规律及轮齿损伤程度的变化过程。负载分担比的变化如图7所示。

图6 不同裂纹深度TVMS变化Fig.6 TVMS changes with different crack depths

图7 不同裂纹深度下负载分担比Fig.7 Load sharing ratio for different crack depths

由图7看出，在不同裂纹深度下，裂纹齿对的负载分担比不同，并对第二个双齿啮合区结果影响较大。在单齿啮合区负载分担比为1，因为此时只有裂纹齿对参与啮合；随着裂纹深度的增加，双齿啮合区负载分担比逐渐降低且变化幅度增大，而造成这一现象的原因为轮齿“死区”范围拓展速度加快，使得裂纹齿对承载能力下降，直接印证了裂纹会缩短齿轮使用寿命并且降低齿轮系统传动质量这一观点。

2.2 沿长度方向拓展裂纹模型的构建及TVMS计算

裂纹在中早期拓展时，并不是等深度且完全贯穿的[5]，会在过渡曲线附近同时沿深度与长度方向拓展，直至完全贯穿整个齿宽。因此，本文针对这一现象，将中早期裂纹模型简化为沿齿宽方向不等深度分布的裂纹模型，如图8a所示，qs与qe分别为始端与尾端裂纹深度。沿齿宽方向将轮齿分割成无数小薄片，任取一小薄片如图8b所示，当该小薄片厚度很小时，裂纹深度是确定的，但小薄片间裂纹深度不断变化且都沿固定角度θ拓展。每一小薄片记为Δx，其厚度与刚度分别为ΔL、Kpiece，健康与故障轮齿所具有的刚度Kthealth与Ktcrack记为

(31)

(32)

(33)

N=L/ΔL

(34)

当只有裂纹齿对参与啮合过程时，时变啮合刚度K记为

(35)

式中，Ka(x)、Kb(x)、Ks(x)与ΔKa(x)、ΔKb(x)、ΔKs(x)分别为整个健康轮齿与裂纹轮齿任一小薄片的轴向压缩刚度、弯曲刚度与剪切刚度；N为被分割后裂纹轮齿小薄片份数，求解时需同时保证结果精确性与运算速度，取N=60。

(a)非均匀分布裂纹悬臂梁模型 (b)切割后裂纹轮齿小薄片图8 非均匀分布裂纹模型Fig.8 Non-uniform distribution crack model

当裂纹沿齿宽方向投影长度小于齿宽时，称为非贯穿型裂纹，反之称为贯穿型裂纹，需同时讨论这两种情形下沿齿宽方向的裂纹深度分布情况，如图8a与图9所示。在裂纹深度(A-A)截面上，建立以初始裂纹萌生点O为坐标原点，OC与OB方向分别为X轴与Y轴的平面直角坐标系，将裂纹深度分布曲线按照抛物线处理，沿长度方向拓展的解析方程计算公式如下。

(1)贯穿型裂纹模型：

(36)

图9 非均匀分布裂纹轨迹Fig.9 Non-uniform distribution crack trajectories

(2)非完全贯穿型裂纹模型：

(37)

在本文中，研究在中度故障程度前提下，分析贯穿型与非贯穿型裂纹对TVMS的变化规律，裂纹参数与其对应的结果分别见表3与图10。

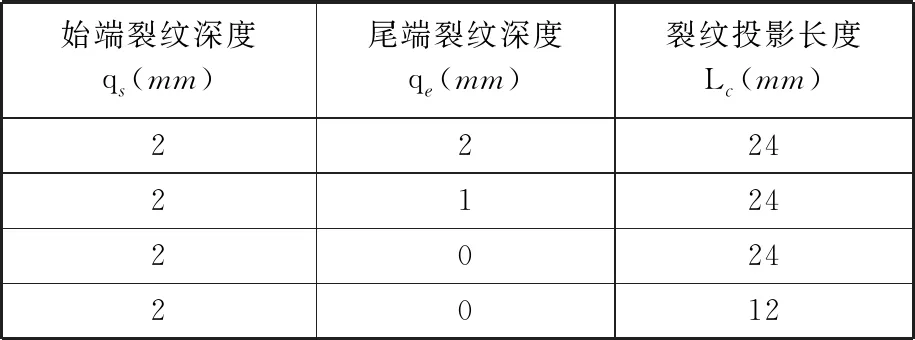
表3 非均匀分布模型裂纹参数

图10 不同裂纹长度TVMS变化Fig.10 TVMS changes with different crack lengths

由图10可知，在初始裂纹深度相同前提下，由不同裂纹尾端深度与裂纹投影长度引起的TVMS不同，且TVMS会随着两者的增加而减小。对比图10结果与图6裂纹深度结果可知，由裂纹长度与尾端深度引起的TVMS变化并不明显；并且对比裂纹深度和裂纹长度对TVMS影响可知，裂纹深度对TVMS影响更大，说明当故障发生在中早期时，由故障产生的刚度激励变化并不明显，导致由轮齿故障引起的动态行为不易被监测。

3 有限元结果验证

3.1 齿轮模型建立及网格划分

以表1参数为基准，在SolidWorks中构建不同故障程度的圆柱直齿轮装配模型，相应故障程度的轮齿部位放大图见图11，模型保存为x_t文件并通过SolidWorks与Workbench接口将齿轮模型导入Workbench瞬态动力学模块中，模型被分割成轮齿与轮体两部分，对三对啮合轮齿的网格进行加密，如图12所示。主动轮和从动轮只具备自身对地的旋转自由度[21]，旋转副采用MPC184单元，接触区采用CONTA174单元和TARGE170单元，齿轮副为四面体与六面体混合网格，即轮体与轮齿网格分别为六面体与四面体。由于轮齿的故障程度不同，采用四面体网格能够适应裂纹复杂形貌，使其求解时具备更好的适应性，此外假定材料为线弹性材料，其余网格设置不变。

(a)q=0 (b)q=1 mm

(c)q=2 mm (d)q=3 mm图11 啮合轮齿放大图Fig.11 Enlargement of meshing gear teeth

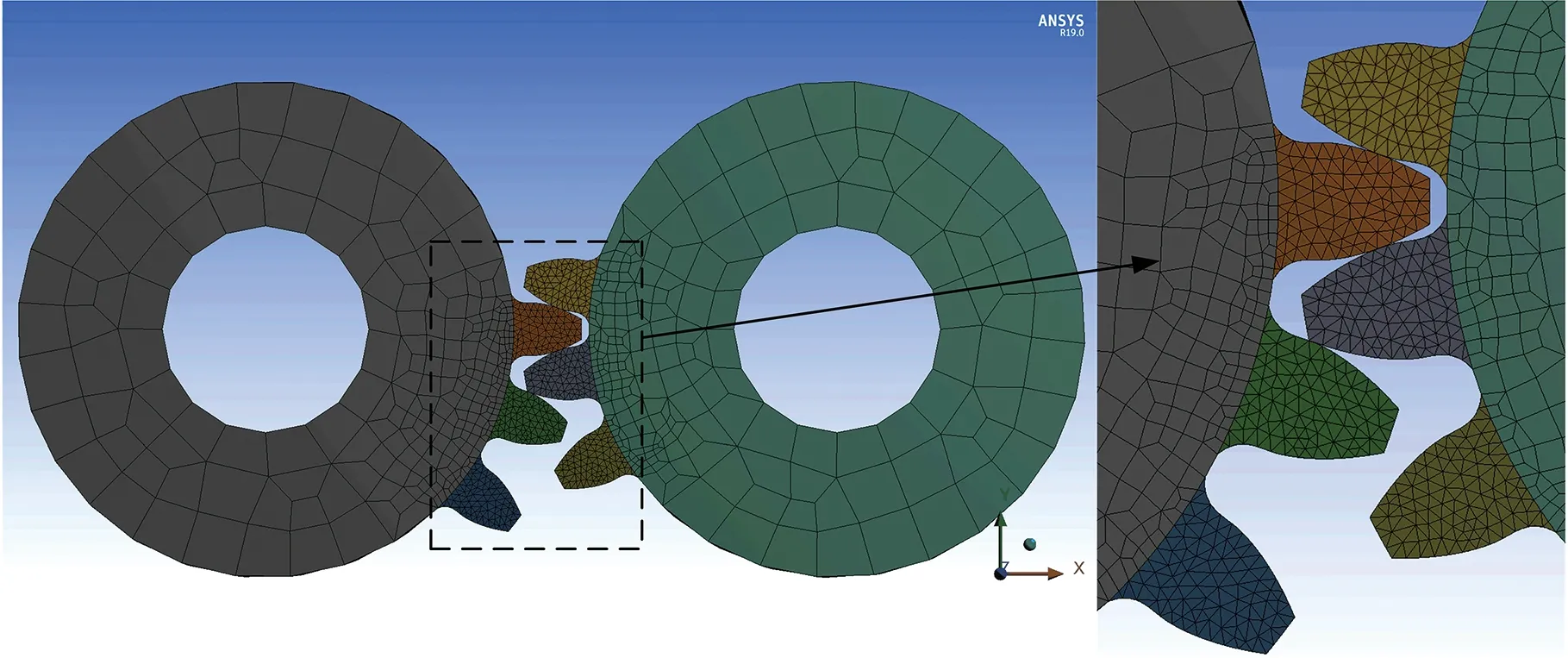
图12 有限元齿轮网格Fig.12 Finite element gear mesh

3.2 有限元法TVMS的求解

为更准确地分析齿轮副动态行为，并对2.1节结果进行验证，在接触设置中，选择互相接触的上下表面分别为接触面与目标面，建立图13所示的无摩擦力两自由度齿轮副动力学参数模型[22]，并将齿轮副简化为带有质量的质心与形心重合的两个圆盘。求解前，需将齿轮模型旋转并使第二对轮齿恰好在初始啮合位置上。求解结束后，提取对应时刻主从动轮轮孔相对旋转角，分别记为θp(t)与θg(t)，由动力学方程可得

(38)

(39)

x(t)=rpbθp(t)-rgbθg(t)-e

(40)

式中，Jp、Jg分别为主、从动轮惯性矩；Tp、Tg分别为驱动力矩与负载力矩；rpb、rgb分别为主、从动轮基圆半径；C(t)、Kt分别为啮合阻尼与啮合刚度；x(t)为轮齿沿啮合线的变形量；2e为齿轮总间隙。

当齿轮副旋转速度较慢时，由齿轮副转动引起的惯性效应及啮合阻尼很小[21]，可剔除式(38)、式(39)与转角相关的导数项，简化后的啮合刚度Kt为

(41)

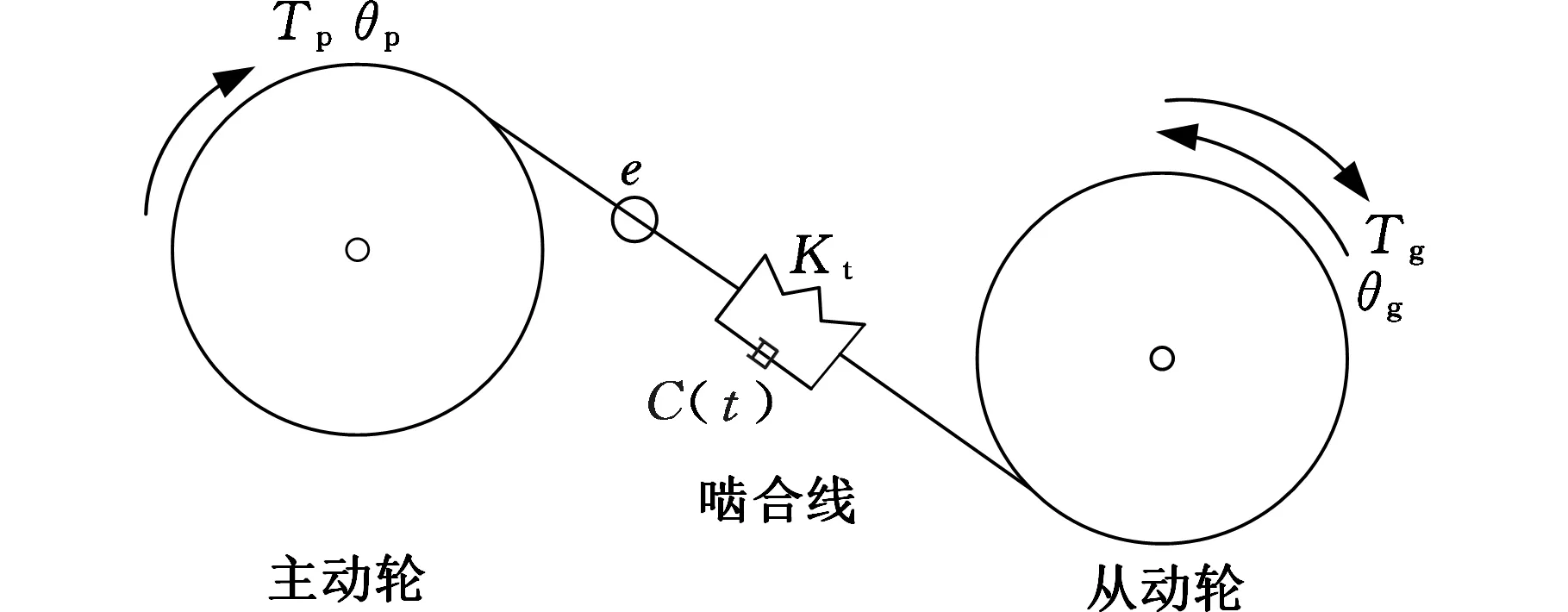
图13 两自由度动力学参数模型Fig.13 2-DOF dynamic parameter model

在前处理阶段，需设置如齿轮转速与扭矩等相关边界条件，本文以第二对轮齿开始啮合到退出啮合的整过程为研究对象，同时结合分析前后两组齿对结果的影响，如图14红色虚线框所示，规定第二对齿开始进入啮合(i=1)时角位移为0，单双齿区角位移范围计算公式如下：

(42)

(43)

θt=2π(Cr-1)/Z1

(44)

(45)

式中，θs、θd分别为主动轮位于单齿啮合区与双齿啮合区轮齿角位移范围；θt为双齿啮合区角位移；Z1为主动轮齿数；Cr为重合度；rai、rbi、ri(i=1, 2)分别为主从动轮齿顶圆、基圆、分度圆半径；α为分度圆压力角。

经式(42)～式(45)计算，确定主动轮旋转角度为0.51 rad，转速为0.51 rad/s，从动轮扭矩为200 N·m，求解时间为1 s，共分为50子步，即针对四种不同的裂纹深度情况，在0～1 s内每隔0.02 s分别采集主、从动轮的轮孔相对旋转角。在后处理阶段，将得到的轮孔相对旋转角导入MATLAB中并根据式(41)计算啮合刚度Kt，结果如图15所示。

图14 轮齿角位移变化Fig.14 Change of tooth angle displacement

图15 有限元分析结果Fig.15 Finite element analysis results

由图15可知，TVMS随裂纹深度增加而降低，且裂纹对单双齿啮合区均有影响，并对第二个双齿啮合区结果影响较大，这与改进的势能法所得结论一致；当裂纹深度达3 mm时，TVMS降幅变大，由于裂纹深度超过轮齿中心线，轮齿上半部分完全失去承载能力。值得注意的是，此时有限元结果存在一个“转接区”，因为在啮合时轮齿处于单双齿啮合交替的过渡阶段，使得齿轮总变形量位于单齿变形量与双齿变形量之间，能够更准确地描述齿轮传动的动态过程。

为研究有限元法与改进势能法结果的差异性，将两者的平均TVMS进行对比，对比结果见表4。当裂纹深度分别为0、1 mm、2 mm、3 mm时，与有限元法所得结果的相对误差分别为5.9%、5.0%、2.6%、3.5%，结果在可接受误差范围内，为齿轮动力学模型的确立提供了一定参考。

表4 势能法与有限元法对比结果

4 结论

(1)本文将轮齿简化为固定在齿根圆变截面的悬臂梁，研究了由齿顶圆弧、渐开线齿廓及过渡曲线构成的完整齿廓曲线。针对传统势能法的局限性，分析了双齿啮合区相邻齿耦合效应对TVMS的影响，将所得结果与另外两种传统算法进行了对比，结果表明传统方法低估了轮齿总变形量，改进势能法能够实现双齿区TVMS的降低。

(2)明确了“死区”出现的原因及危害性，探索了最大拉应力点(材料失效部位)出现的位置。研究了裂纹对截面面积及惯性矩的影响并推导了相应的计算公式，提出了一种沿深度方向拓展的裂纹路径，分析了不同深度下的TVMS及负载分担比的变化规律。研究了中早期故障程度下裂纹同时沿深度和长度方向拓展的情况，构建了一种非均匀分布裂纹模型并提出相应的TVMS计算方法，结果表明TVMS对裂纹深度较为敏感，而对裂纹长度的敏感性较差。

(3)构建了两自由度齿轮传动系统动力学参数模型，在ANSYS Workbench瞬态动力学模块提取主从动轮轮孔相对旋转角，并求得TVMS大小。结果表明有限元法与势能法结果较为吻合，误差均在6%的范围内。

本文仅考虑了裂纹对TVMS的影响规律，下一步研究由裂纹故障引起的动力学响应并分析相应的故障特征，进而讨论多种评价指标(时域、频域)的变化趋势，从而实现裂纹故障早期故障诊断的目的。