多重对比，让计算学习走向深入——以人教版二年级下册『除法竖式』为例

文 张慧

《义务教育数学课程标准（2022年版）》中提出：“数的运算重点在于理解算理、掌握算法，数与运算之间有密切的关联。”学生在计算的学习过程中不仅要掌握算法，明晰算理，还要感悟计算的本质，建立计算知识体系，从而实现深度学习。刘月霞教授在《深度学习：走向核心素养（理论普及读本）》中指出：“在深度学习中，学生掌握学科的核心知识，理解学习的过程，把握学科的本质及思想方法，形成积极的内在学习动机、高级的社会性情感、积极的态度、正确的价值观，成为既具独立性、批判性、创造性又有合作精神，基础扎实的优秀的学习者，成为未来社会历史实践的主人。”可见，深度学习着眼于学生对于知识的迁移和对知识整体的把握，并重视学生思维和情感的提升。

四则运算中难度最大的是除法，学生在描述书写过程和计算中有一定的困难。除法竖式的形式较为特殊，因此掌握其算法、理解其算理都存在一定的困难。人教版二年级下册教材第六单元中第一次出现了“除法竖式”，学生在掌握竖式计算方法和理解算理的过程中遇到困难。原因有三：其一，除法竖式的书写格式与学生本节课前学习的加、减、乘法竖式不一样；其二，除法竖式中被除数、除数、商、余数的书写位置没有按照横式的顺序进行排列；其三，学生难于从除法竖式中直接观察到平均分的过程。比较是一切理解和一切思维的基础，对于难理解和难掌握除法竖式的学习来说，教师可以让学生在多次对比的过程中理解除法竖式的计算过程，建立起除法横式与除法竖式之间的联系，从而深化对除法竖式模型的理解和掌握。

一、对比竖式图形，解析除法竖式过程

逻辑并不产生于语言，而是可以从动作的普遍协调中找到其较深的起源，计算思维是一种逻辑推理，学生在算理的学习中就要借助动作来经历逻辑推理过程，从而形成计算思维。小学生的思维大多处于具体运算阶段，在此阶段中，学生要借助具体的表象来表征抽象的运算，从而理解运算的道理。小学数学计算是十分抽象的，其竖式的书写规则是约定俗成的，学生不能够直接体会其优势。几何直观作为理解计算的脚手架，是连接竖式计算外在形式和内在算理的桥梁。在“除法竖式”一课的教学中，教师在学生列横式计算后创设“有13 个车轮，组装1 辆车用4 个车轮，可以组装几辆车？”的情境，为学生提供竖式计算的机会，并让学生借助操作圆片解析竖式计算过程。

师：（如图1）这位同学列的竖式就是数学上规定的除法竖式，它与我们以前学习的加法、减法和乘法竖式不一样，你能看懂这个竖式吗？请你借助圆片摆出竖式计算的过程，一边摆一边说竖式里面的每一个数表示什么？

借助已有学习经验，学生摆出图2，边摆边解释图1 竖式计算的过程。

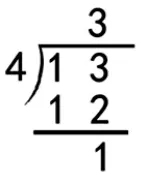
图1

图2

师：结合图来说说，竖式里的13、4、3、12 和1 分别表示什么？

生：13 是被除数，是表示车轮的总数，是所有圆片数。

生：4 是除数，是每辆车有4个车轮，是一辆的车轮数。

生：3 是商，是可以装3 辆车，一共有3 辆。

生：12 是3×4 的积，是用掉的车轮。

生：1 是余数，是分剩下的车轮。

借助分圆片的操作过程，学生将抽象的除法竖式计算过程具体化。竖式计算的过程较为抽象，学生不能够直接理解其过程中的各数是什么意思，尤其是12，只有在竖式中有所体现，无法在横式中找到。学生借助操作经历平均分的过程，找到了竖式中的除数4和商3，也找到了12 的原型，是3个4，即组装3 辆车用掉的车轮数。在本环节中，学生通过摆一摆、圈一圈等活动，将平均分的过程与竖式计算的过程相结合，就能够理解竖式计算中的每一个数字表示的含义。

二、对比横式竖式，感悟竖式的完整性

比学什么更重要的是学生已经知道了什么，学生在学习新知识过程中一定要迁移旧的知识与方法。知识迁移是学习数学最重要的方法之一，任何数学知识学习之前，学生都有着一定数学学习和生活经验的基础。如学生在学习列除法竖式前已经学习了列横式计算有余数的除法，知道除法横式中各部分的名称，能列出“13÷4＝3（辆）……1（个）”的算式，求出组装3 辆车，还剩1 个车轮。但是横式计算有局限，其无法呈现竖式计算的全过程。对于第一次接触除法竖式的学生来说，初步理解和掌握除法竖式计算模型是本节课的重难点之一。因此，教师在教学前要充分把握学生的知识起点，找准学生知识的生长点。学生要迁移除法横式的学习经验学习竖式，将除法竖式中各部分名称与横式相对应，从而感悟除法竖式能够完整清晰地体现除法竖式的计算过程。

师：观察横式和竖式，它们有什么相同与不同？

生：横式里的被除数、除数、商和余数在竖式里面也有。

生：竖式比横式多了一个12，12 是3×4 的积。

师：横式与竖式表示的道理都一样，只不过竖式能够清楚地表示出除法计算的过程。

学生在学习竖式前是用横式表示除法计算的，在学习竖式后，学生学会用竖式来表示计算的过程，也能够详细描述除法竖式的算法。除法横式是旧知识，竖式是新知识，在教学中教师应该引导学生借助对比的手段在新旧知识之间形成联系，使得除法竖式各部分与横式的各部分一一对应起来，从而借助横式来理解竖式的计算过程。此外，在学习除法竖式的过程中，教师要引导学生将横式和竖式进行对比，区分横式与竖式各自的优势，感悟竖式不仅能够体现除法各个部分，还能够体现除法计算的过程，即感悟竖式的完整性。

三、对比正误格式，巩固除法竖式表象

相对于加法、减法和乘法来说，除法竖式的模型更难于掌握，学生尝试竖式计算除法时更容易迁移加法、减法和乘法竖式模型来计算除法。世界各国的除法竖式模型不尽相同，但是无论模型外在形式是怎样，其都要在竖式计算的过程中体现除法计算的过程，体现出计算方法。在竖式计算的学习过程中，学生需要记忆竖式计算的过程，也要经历知识的再认与辨析等。除法竖式计算过程对于二年级的学生来说稍复杂，学生在刚学习除法竖式时难免会出现两种错误。其一，是迁移加、减、乘法竖式计算的模型，将除法竖式写成乘法竖式的形式（如图3）；其二，是漏掉除法的计算过程，只体现被除数、除数、商和余数（如图4）。

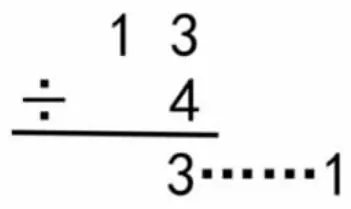
图3

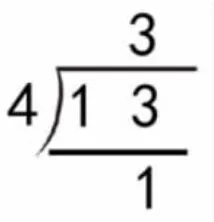
图4

学生迁移原有旧知识来帮助自己理解和掌握新知识，在除法竖式的学习中，学生也会迁移加法、减法、乘法的模型来构建除法竖式。但是，受除法计算特殊性影响，除法竖式计算的外在表现形式与其他三种运算不同。因此，教师在发现学生迁移其他竖式的形式来计算除法时要将其与正确除法竖式格式进行对比，帮助学生建立正确的除法竖式模型。

师：想一想，刚才老师为什么没有选择这个除法竖式（图3）？

生：它没有表示出3×4 的积是12。

师：原来这个竖式（图3）没有表示出除法计算的过程，它不够完整。

除法竖式的书写格式是人为约定的，约定的正确书写格式能够完整体现除法计算过程的形式。对比正误，学生不仅加深了对除法竖式外在形式的印象，还可以更加深入地理解各部分所表示的含义。此外，在二年级的除法竖式计算中，学生经常在商的书写位置上出现错误，学生会将商与十位和个位的中间对齐，且这个错误常常会持续很久，甚至会保持到五年级学“小数除法”时。由此可见，学生对于商书写位置的理解需要加强。针对这种现象，教师同样可以借助对比的方法，让学生对比两种商的书写位置并说一说哪种书写是正确的。借助直观图，学生能够说出除得的3 表示的是3 辆车，而不是30 辆车，所以应该与个位对齐。学生在对比辨析中，不仅能够深化对正确书写格式的记忆，还可以进一步说理，再次深入分析除法竖式计算的算理巩固算法，从而培养学生的批判精神。

四、对比有无余数，深化除法竖式模型

除法的本质是等分计数单位，刚好分完是等分的一种特殊情况，大部分的整数除法都是有剩余的，写在除法横式中就是余数。学生在除法竖式中容易出现两种错误：其一，剩余的数大于或者等于除数；其二，没有剩余时，忘记用0 来占位。针对学生容易走进的误区，教师在教学过程中要准确把握教学重难点和学生的易错点，着重介绍除法计算中的余数。除法计算的最后一步就是看有没有剩余，如果有余数，就在竖式的最后一行写下余数，如果刚好除尽，没有剩余，就在余数的位置写0 来占位。在学习除法竖式的过程中，学生要经过有无余数的对比，才能够体验余数的产生过程，也就能够理解没有余数还要写一个0 来占位的道理。

师：对比13÷4 和16÷4 这两道题的竖式（如图1、图5），它们有什么不同？

图5

生：13÷4 的横式和竖式中都有余数，16÷4 的横式和竖式中都没有余数。

生：13÷4 没有分完，所以有余数；16÷4 正好分完，所以没有余数。

生：被除数比除数与商的积大时，有余数；被除数和除数与商的积一样时没有余数。

通过对比，学生发现，余数就是等分后的剩余，刚好分完就没有余数；平均分到不能够再分还有剩余，剩余的部分就是余数。学生在观察竖式的过程中发现，竖式的书写是十分完整的，无论有没有余数，都要写出一个数来表示剩余情况，0 就是没有剩余，非0 就是有剩余，而以前学习的横式则采用直接不写余数来体现没有剩余。可见，除法竖式对除法过程描述更加详细。对比有无剩余的横式竖式，学生进一步发现了除法竖式的优势，采用的除法竖式不仅能将除法的各个部分体现出来，还能够完整体现除法计算的全过程，进一步深化对除法计算的理解。

对比是小学数学学习的一个重要方法。通过对比学习计算，学生能够深入理解各种计算的相同和不同，领悟计算之间的关联，感悟计算的一致性。因此，小学计算学习过程中，教师要引导学生进行多角度对比。对比正误，经历计算知识的形成过程；对比同一种计算的不同外在形式来掌握计算方法；对比计算与几何直观，深入理解算理；对比不同计算之间的相同与不同，使抽象的除法计算越来越具体、清晰。在充分对比的计算学习中，学生凭借多角度对比建立竖式表象、巩固竖式模型，经历计算推理过程，从而实现运算能力的提升，促进自身深度学习的发生。