基于效率修正的变频压缩机性能模型开发

赵康佐，周永戬，胡海涛*，管斌

（1-上海交通大学制冷与低温研究所，上海 200240；2-上海交通大学新能源动力研究所，上海 200240）

[关键字] 效率修正；变频；压缩机；模型

0 引言

变频空调因其节能和优异的性能，近年来得到了越来越广泛的应用[1]，针对变频空调的研究也越来越多[2-3]。与传统的定频空调相比，变频空调的主要区别是采用了变频压缩机。压缩机是系统的核心部件，为整个系统提供动力[4]。因此，研究变频压缩机是研究变频空调系统仿真的关键。

目前常用的压缩机模型主要有理论模型、经验模型和半经验模型。其中，理论模型完全基于理论，主要为全动态模型、准动态模型和全稳态模型。全动态模型考虑到的细节较多，模型比较复杂，会影响计算时间和稳定性[5]。全稳态模型应用于系统仿真可以较好反映流量和功率[6]，但是没有考虑压缩机排气温度与压缩机壳体换热之间的关系，导致计算误差较大[7-8]。准动态模型可以反映压缩机的部分动态特性，相较于全动态模型速度较快，但应用于系统仿真中仍过于复杂，无法满足要求[9-10]。经验模型主要为系数拟合模型等[11]，如针对定频压缩机的“十系数”模型[12]和针对变频压缩机的“二十系数”模型。经验模型的建立完全基于实验结果，通过拟合得到目标参数与实验参数的关系式，其中的参数没有任何的物理意义[13]。经验模型的优点是计算速度较快，但缺点是在预测实验工况范围之外的工况时，精度会急剧下降[14]。半经验模型从理论模型出发，通过推广理论模型，将其转换为可以进行拟合或修正的形式，将该形式理论模型中的某些性能参数用数据拟合公式表示。半经验模型通过拟合参数提升了计算速度、计算精度和适用范围，具有一定物理意义，因此适用于压缩机的系统仿真[15]。目前已有的半经验模型，大多采用神经网络或多项式拟合[16]，缺乏明确的物理意义，数据需求量大，并且没有通用的表达式。

本文在定频半经验模型的基础上，建立了基于效率修正的变频压缩机模型，并对模型的精度进行了验证，分析了模型的拟合性能和外推预测性能。

1 基于效率修正的变频压缩机流量计算模型

通过将压缩机容积效率作为中间参数，建立变频压缩机流量与定频压缩机流量联系，进而建立变频压缩机流量模型，具体形式为：

式中，m为质量流量，kg/s；mref为基准频率下的质量流量，kg/s；f为频率，Hz；fref为基准频率，Hz；ηv为容积效率；ηv,ref为基准频率下容积效率。

通过将变频压缩机容积效率与频率进行归一化处理，得到归一化容积效率与归一化频率的关系，如图1所示。由图1可知，归一化的容积效率与频率之间的关系可以用二次多项式来表示：

图1 归一化容积效率与频率关系

式中，a1、a2和a3为拟合系数。

定频压缩机理论流量可以表达为：

式中，Vdisp为理论排气量，m3；vsuc为吸气比容，m3/kg。

容积效率ηv与压缩机压缩比的关系[17]：

式中，pdis为排气压力，kPa；psuc为吸气压力，kPa；b1、b2为拟合系数。

因此，基频下压缩机的质量流量可由式(5)计算：

将定频压缩机流量及归一化容积效率代入式(1)，即可得到变频压缩机流量显式计算公式：

综上所述，基于效率修正的变频压缩机流量计算模型建立过程为：1）设计压缩机使用工况范围，在范围内进行可能工况的台架实验或仿真计算，将得到的数据作为基于效率修正的质量流量模型数据源；2）观察数据源并选取合适的基频；3）在基频下建立压缩机定频率模型并进行拟合得到拟合系数b1和b2；4）对源数据的容积效率及频率进行归一化处理，并建立变频率归一化容积效率的关系模型，进行拟合得到拟合系数a1、a2和a3。

2 基于效率修正的变频压缩机功率计算模型

通过将压缩机等熵效率作为中间参数，建立变频压缩机功率与定频压缩机功率联系，进而建立变频压缩机功率模型，具体形式为：

式中，W为压缩机功率，W；Wref为基准频率下的压缩机功率，W；ηis为等熵效率；ηis,ref为基准频率下的等熵效率。

通过将变频压缩机等熵效率与频率进行归一化处理，得到归一化等熵效率与归一化频率的关系，如图2所示。

图2 归一化等熵效率与频率关系

由图2可知，归一化等熵效率与频率关系式：

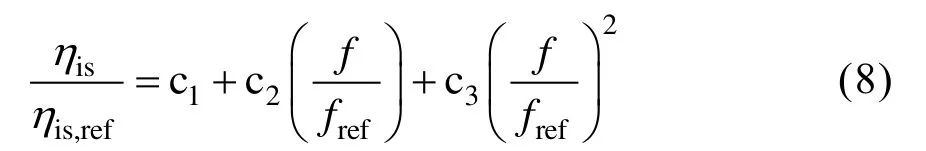
式中，c1、c2和c3为拟合系数。

基频下的压缩机功率可以表示为理论输入功率和损耗功率的函数，基频下压缩机的功率为：

式中，Wt为理论输入功率，W；Wloss为恒定损耗功率，W；α为损耗系数。

通过引入拟合系数d1、d2，式(9)可简化为：

Wt采用式(11)可以平衡物理模型与多项式回归精度，达到良好的拟合精度[17]：

式中，psuc为吸气压力，kPa；pdis为排气压力，kPa；Vsuc为吸气体积流量，m3/s；n为多变系数。

为了进一步简化理论输入功率Wt的表示形式，降低计算复杂度，将难以显式计算的高阶非线性项以拟合系数进行替代，即令拟合系数d3=(n-1)/n，可将基频下压缩机功率表示为式(12)：

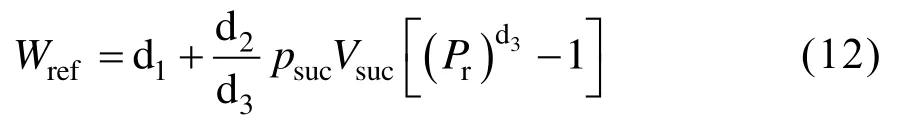
式中，d1、d2和d3为拟合系数；Pr为压缩比。

将定频压缩机功率及归一化等熵效率代入式(7)，即可以得到变频压缩机功率显式计算公式：

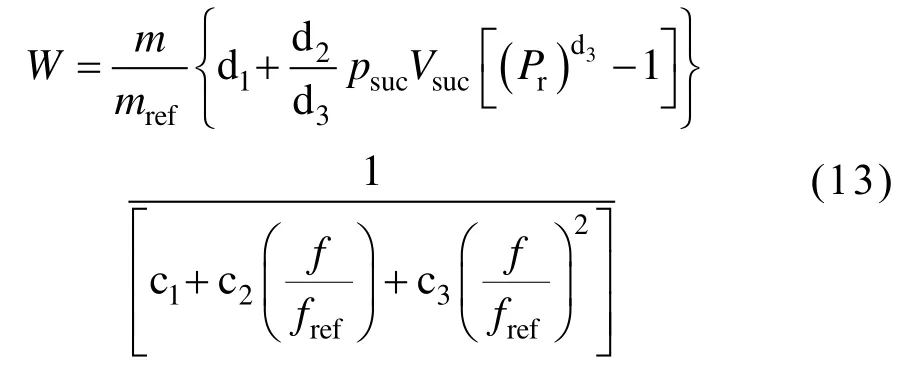
综上所述，基于效率修正的变频压缩机功率计算模型建立过程为：1）选取压缩机使用工况范围，利用产品数据或其他方式得到用于功率模型拟合的数据源；2）观察数据源并选取合适的基频；3）在基频下建立压缩机定频率模型并进行拟合得到拟合系数d1、d2和d3；4）对源数据的等熵效率及频率进行归一化处理，并建立变频率归一化等熵效率的关系模型，进行拟合得到拟合系数c1、c2和c3。

3 变频压缩机排气温度计算模型

变频压缩机排气温度可以表示为排气压力及工质出口焓的函数：

式中，Tdis为压缩机排气温度，K；hdis为压缩机排气焓，kJ/kg；f为物性计算函数。

通过压缩机的能量平衡建立出口焓值和压缩机做功的关系：

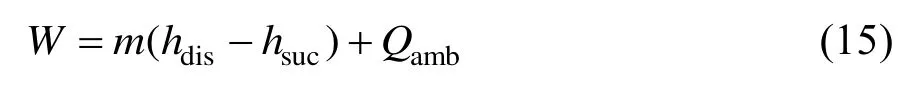
式中，Qamb为压缩机与环境换热量，kW；hsuc为压缩机吸气焓，kJ/kg。

当确定压缩机功率W，质量流量m，吸气焓值hsuc，换热量Qamb即可计算得到出口焓值hdis。

压缩机与环境的换热量Qamb可以按式(16)计算：

式中，U为压缩机壳体的平均传热系数，kW/(m2·K)；Ashell为压缩机壳体传热面积，m2；Tshell为压缩机壳体温度，K；Tamb为环境温度，K。

压缩机壳体温度Tshell可表示为式(17)[18]：

式中，e1、e2和e3为拟合系数。

4 变频压缩机模型精度验证

为验证基于效率修正的变频压缩机流量、功率以及排气温度模型的精度，本文采用文献[16, 19]中的数据与模型预测结果进行对比，工质为R22，压缩机参数及测试工况见表1。

表1 压缩机参数及测试工况

流量模型中，拟合系数a1、a2、a3、b1和b2分别为0.706 7、0.422 9、-0.128 6、0.964 57和-0.045 40；功率模型中，拟合系数c1、c2、c3、d1、d2和d3分别为0.313 2、1.127 1、-0.439 2、171.978 7、1 270.540 5和0.405 2；排气温度模型中，拟合系数e1、e2和e3分别为126.053 5、5.942 4和110 296.041。

验证的运行工况为-10～15 ℃，冷凝温度为30、40、50和6 ℃，频率范围为30～120 Hz。

图3～图5所示分别为变频压缩机流量、功率和排气温度模型的精度验证结果。可知对于质量流量，平均误差为0.75%，而最大误差为3.06%，总体误差在±5%以内；对于功率，平均误差为1.45%，而最大误差为-7.15%，总体误差基本在±5%以内；对于排气温度，最大误差为4.5 ℃，总体误差基本在±4 ℃以内。因此3个模型均达到较好的预测效果。

图3 变频压缩机质量流量模型精度验证

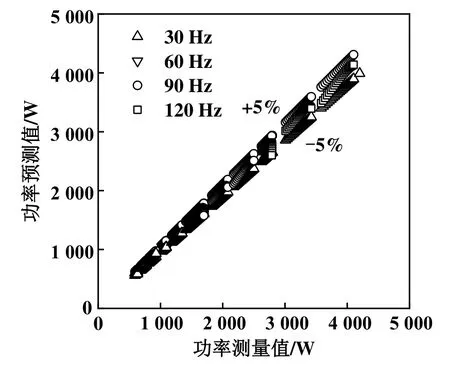
图4 变频压缩机功率模型精度验证

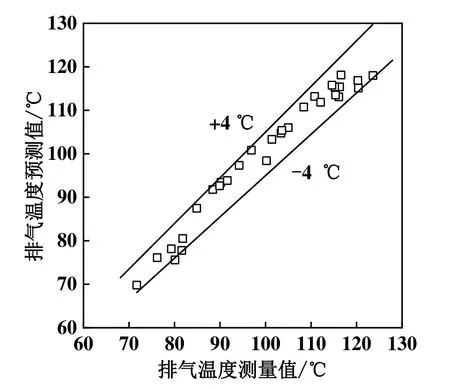
图5 变频压缩机排气温度模型精度验证

5 变频压缩机模型的优势分析

5.1 模型所需数据量的优势分析

为了验证模型在不同数量的源数据下，能否达到拟合的精度要求，需对模型拟合性能进行分析。如果数据量太少，拟合模型无法满足精度要求；如果数据量太多，不但耗费了多余的时间和人力资源，而且容易发生过拟合现象。为了找到模型欠拟合的临界点，本文分别随机选取10、20、30、40、50和60组数据进行拟合。平均预测误差的计算式为：

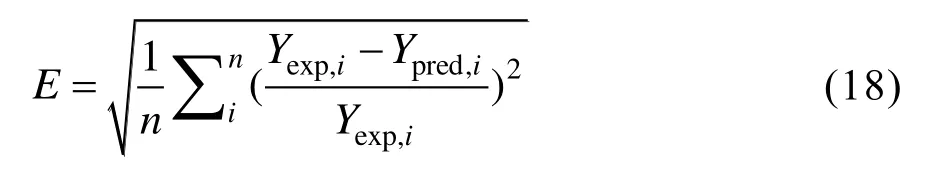
式中，E为平均预测误差；Yexp,i为质量流量或功率的实验值；Ypred,i为质量流量或功率的预测值。

图6所示为不同拟合数据量下的压缩机模型预测误差。由图6可知，随拟合数据量增加，模型预测偏差快速下降。当数据量达到20组时，预测精度达到稳定，推荐采用20组实验数据拟合模型，这比已有研究[20]下降了50%以上。对于质量流量和功率，平均预测误差分别为0.75%和1.45%，最大预测误差分别为3.0%和7.1%，表明基于理论推导的模型形式能够反映压缩机实际工作的物理过程。

图6 不同拟合数据量下的压缩机模型预测误差

5.2 变频压缩机模型外推预测性能分析

为了研究本文建立的变频压缩机外推预测性能，将变频率工况分为两组，一组用于拟合基于效率修正的变频压缩机模型，一组用于测试模型在未拟合部分数据的预测性能。在30、60、90和120 Hz四组变频数据中分别选取30 Hz、120 Hz组作为测试数据，其余组作为拟合数据。图7所示为30 Hz、120 Hz时质量流量模型验证。图8所示为30 Hz、120 Hz时功率模型验证。由图7和图8可知，在30 Hz和120 Hz测试数据集中，质量流量的平均预测误差分别为1.06%和0.95%，最大预测误差分别为-3.40%和-2.42%；功率的平均预测误差分别为1.33%和1.55%，最大预测误差分别为-7.84%和6.89%，其中95.9%的预测误差小于±5%。

图7 30 Hz、120 Hz频率时，质量流量模型验证

图8 30 Hz、120 Hz频率时，功率模型验证

综上所述，模型对于外推的预测性能良好，其中模型对于120 Hz的外推性能要优于对30 Hz的外推性能，这说明本模型在考虑拓展应用时应优先考虑高频率外推。

6 结论

本文建立了基于效率修正的变频压缩机质量流量模型、功率模型和排气温度计算模型，对模型的精度进行了验证，并对模型的拟合性能做出了分析，得出如下结论：

1）对模型的精度验证结果表明，压缩机定频模型对质量流量的预测偏差在±2%以内，对功率的预测偏差在±3%以内，变频模型对质量流量预测偏差小于±5%，对功率的预测偏差基本小于±5%，对排气温度的预测偏差小于±5 ℃；

2）模型在20组及以上拟合数据量下可以达到稳定良好的拟合精度，拟合性能良好；

3）外推验证表明，模型对于质量流量的平均预测误差为1.06%，对于功率的平均预测误差为1.33%，其中95.9%的预测结果在±5%范围内，外推预测性能良好。