基于运行数据的冷水机组系统建模及优化控制

胡蓝青，晋欣桥，杜志敏

（上海交通大学制冷与低温工程研究所，上海 200240）

0 引言

由于全世界的能源紧张问题逐渐严峻，节能问题已经越来越受到世界各国关注。根据联合国环境计划署统计，建筑能耗约占总能源消耗的40%以上[1]。近些年来的研究与实践表明，建筑节能是缓解能源供应不足最有效的措施[2]。从建筑能耗的构成来看，暖通空调系统（Heating, Ventilation and Air conditioning，HVAC）能耗是建筑能耗最大的组成部分，约占建筑总能耗的65%左右。因此，降低空调系统能耗是建筑节能的重要组成部分。在冷负荷需求一定和空调系统设计不变时，对空调系统进行优化控制是降低空调系统能耗的重要途径。

对空调系统的进行优化控制，需要建立能够实时预测空调系统运行特性的能耗预测模型。当前空调系统建模方法主要可分为黑箱模型法、物理模型法和灰箱模型法，其中灰箱模型建模方法介于黑箱模型建模方法和物理模型建模方法之间[3]。对于物理模型建模方法，主要的仿真平台包括BLAST、DOE、TRNSYS和Energyplus等。胡玮等[4]利用TRNSYS建立了大厦某层的多区域建筑及其中央空调系统能耗仿真模型。杨臣等[5]利用建筑能耗仿真软件Energyplus和Designbuilder对某机场建筑及其空调系统建立了仿真模型。但是物理模型中需要的多个参数难以获取，且仿真计算相对复杂，难以用于优化控制计算中。由于多数暖通空调配备了建筑能源监管系统，能够不断采集并记录系统的运行数据，使获取大批量的运行数据成为可能。黑箱模型以大量运行数据为基础，常常通过神经网络、向量机等方法进行仿真建模。龙海燕等[6]利用反向人工神经网络的非线性映射能力建立了中央空调系统制冷机的能量消耗模型。YANG等[7]采用回归树和支持向量机建立冷水机组能耗预测模型，并对两种方法的建模效果进行比较。这些模型与实际系统物理模型无任何物理意义的关联，模型预测的准确度取决于参数的学习、辨识和训练，容易出现泛化能力差等问题。与上述建模方法相比，在数据量充足时，采用基于一定物理意义的经验模型回归拟合的建模方法，不仅可以避免繁琐的参数训练过程，还能够提高计算速度，适用于空调系统的控制计算。

目前国内外不少学者建模时采用基于运行数据对经验模型拟合的方法，并且能够保证模型的准确性与合理性。LEE等[8]利用2 000多组实测数据拟合得到离心式冷水机组性能与水流量之间的经验关系式，并对此经验关系式作为预测模型时的准确性及适用性进行了验证。潘高峰[9]采用最小二乘法与多元线性回归法对电空调与非电空调进行了建模，并通过实例对模型的合理性进行了验证。龚明启[10]采用经验模型对空调系统中的冷水机组、冷却塔等部件进行拟合，并采用遗传算法对整个空调系统进行优化。LU等[11-12]分别对冷水机组和输送设备建立了参数辨识模型。LEE等[13]通过实验得到了冷水机组各种工况下的运行数据，并采用多项式拟合的方法得到冷水机组性能与水流量间的数学表达式。在基于运行数据的建模方法中，历史数据的质量好坏与模型的准确性，因此在建立模型之前，有必要对历史运行数据进行处理。

本文以某自动化生产车间的多冷水机组系统为研究对象，对历史运行数据的数据处理和基于设备经验模型的回归拟合，建立系统的能耗预测模型。为了验证模型的可用性，本文将其应用于基于粒子群优化（Particle Swarm Optimization，PSO）算法的冷水机组系统优化控制策略中，并将该策略与常规顺序启停策略进行比较。

1 运行数据处理

在实际的数据监测过程中，受到系统复杂性、外界干扰和传感器故障等因素的影响，空调系统实际的运行数据存在数据缺失、数据异常和数据量庞大等问题。因此，在利用这些数据之前，必须进行数据处理。对于数据缺失问题，由于缺失数据比例占数据总量的比例很小，因此对缺失数据直接进行删除。对于数据异常问题，本文局部异常因子算法进行异常数据清洗处理。庞大的运行数据量会带来巨大的计算需求，为减少计算量以适应于控制的需要，可以利用系统各运行参数之间存在的关联性和耦合性，采用Boruta能耗特征选择方法将高维度的运行数据进行降维，从而提高计算速度。

1.1 基于局部异常因子算法的数据清洗

局部异常因子算法（Local Outlier Factor，LOF）是一种基于密度的局部异常值识别算法。该算法将某一点的局部密度与其邻域点的局部密度进行比较，如果前者明显低于后者，说明该点位于比其相邻点更稀疏的区域，代表该点是一个异常点。本文使用LOF算法进行对异常数据的清洗工作，并对被识别出的异常数据进行删除。

根据离心式水泵的相似理论，冷却水泵的频率与流量之间存在一条关系曲线。以某冷却水泵为例，图1所示为某水泵频率和功率的原始数据分布情况。

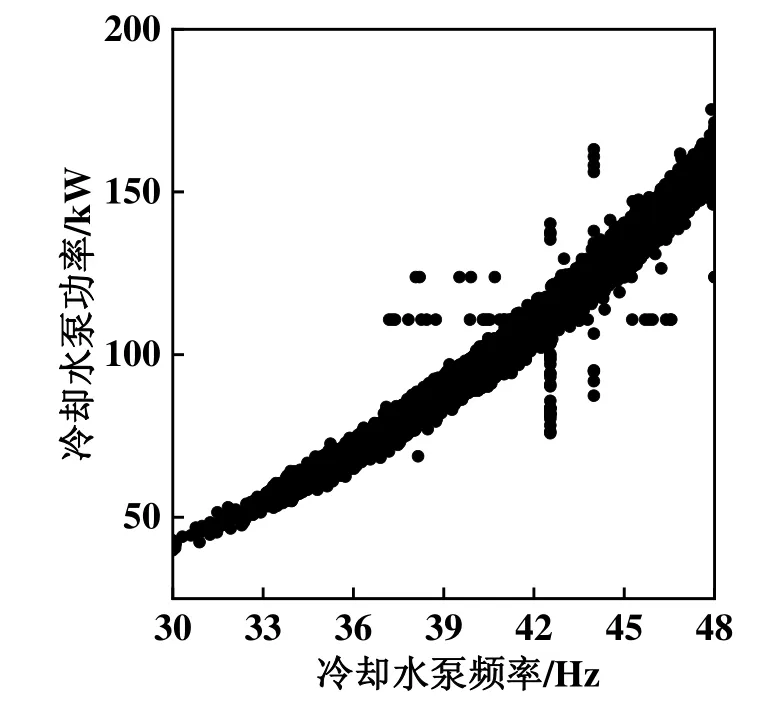
图1 冷却水泵原始数据分布

由图1可知，有部分数据点偏离了绝大部分数据所在的曲线区域，且分布较为稀疏。图2所示为基于LOF算法的异常数据清洗结果，LOF算法将偏离冷却水泵频率-功率关系曲线的数据识别为异常值，去除异常值之后的数据分布符合冷却水泵的频率与流量之间的关系曲线，说明LOF算法在可以准确识别出运行过程中产生的异常数据。

图2 冷却水泵异常数据清洗结果

1.2 基于Boruta能耗特征选择算法的数据降维

数据降维是保留高维度数据最重要的一些特征，去除不重要的特征。在空调运行数据中，冷水机组的功率（P）、负荷（Q）、冷却水进水温度（tcdw,in）、冷却水出水温度（tcdw,out）、冷冻水进水温度（tchw,in）、冷冻水出水温度（tchw,out）、蒸发温度（tevap）和冷凝温度（tcond）存在一定的关联性与耦合性，对以上高维度数据进行降维将大大降低计算成本。冷水机组部分运行数据如表1所示。

表1 冷水机组部分运行数据

特征选择算法广泛应用于高维数据降维领域当中，而Boruta算法是特征选择算法中性能较好的方法，因此通过使用Boruta算法进行能耗特征选择，从而实现高维数据的降维。Boruta能耗特征选择算法基于随机森林分类器[14]，能够挖掘出与对能耗影响最大的运行参数，从而简化模型，降低计算成本。

基于Boruta特征选择算法的数据降维过程步骤：1）对原始数据集进行复制得到复制数据集；2）复制数据集中的每一列都独立地进行随机行变换，得到阴影特征数据集；3）原始数据集与阴影特征数据集进行合并得到混合样本；4）随机选取数据样本和特征组成随机森林，使用随机森林对数据集进行训练并得到各个特征的重要度值。

在所有的原始特征中，特征重要度大于该最大的影子特征重要度值的记为重要特征，特征重要度小于该最大的影子特征重要度值的记为不重要特征。对于不重要特征或者重要度值较低的特征，在建模过程中可以选择舍弃。

使用Boruta能耗特征选择算法可以计算出与冷水机组功率有关的所有特征的重要度。如图3所示，S1、S2和S3分别代表阴影特征最高重要度、阴影特征平均重要度和阴影特征最低重要度；X1～X7依次为负荷（Q）、冷冻水出水温度（tchw,out）、冷却水进水温度（tcdw,in）、冷冻水进水温度（tchw,in）、冷却水出水温度（tcdw,out）、蒸发温度（tevap）和冷凝温度（tcond）。冷凝温度（tcond）是不重要特征，蒸发温度（tevap）、冷却水出水温度（tcdw,out）和冷冻水进水温度（tchw,in）的重要度值较低，冷却水进水温度（tcdw,in）、冷冻水出水温度（tchw,out）和负荷（Q）的重要度值较高。使用Boruta能耗特征提取方法找到了与冷机功率关系最紧密的重要特征：负荷（Q）、冷却水进水温度（tcdw,in）、冷冻水出水温度（tchw,out）。

图3 冷水机组能耗特征重要度

2 多冷水机组系统建模

本文的研究对象是某自动化生产车间的多冷水机组系统，系统结构如图4所示。该多冷水机组水系统包括4台冷水机组（CH1～CH4），冷水机组的冷冻水侧并联配置4台相同型号的变频离心泵（CHP1～CHP4），冷却水侧并联配置4台相同型号的变频离心泵（CDP1～ CDP4），冷却水通过4台相同型号的湿式冷却塔（CT1～CT4）进行散热。

图4 多冷水机组系统

2.1 冷却塔建模

中央空调冷却塔是一种利用冷却水和空气的接触，将空调系统的废热通过冷却水降温的方式排出的换热设备。在冷却塔的散热模型研究中，最常用的是Branu提出的冷却塔模型[15]。Branu模型是在冷却塔用效能-传热单元数法模型的基础上，采用机理分析法建立的模型，可以准确反映出冷却塔的散热过程。Branu模型的数学表达式如式(1)：

式中，εa为冷却塔的热交换率；Ma为空气的质量流量，kg/s；hs,w,in为饱和空气在冷却塔入口水温下的焓值，kJ/kg；ha,in为入口空气的焓值，kJ/kg。

对于逆流式冷却塔，当刘易斯数等于1时，其热交换率εa可以表示为：

式中，NTU为传热单元数Mw为冷却水的质量流量，kg/s；c、n为冷却塔散热模型的经验常数。

式中，M*为空气与水的热效率比；cp为常压下水的比热容，kJ/(kg·℃)。

cs为饱和空气焓值与温度的微分，可表达为：

式中，hs,w,in为饱和空气在冷却塔出口水温下的焓值，kJ/kg；Tcdw，in为冷却水进水温度，℃；Tcdw，out为冷却水出水温度，℃。

2.2 离心水泵能耗建模

离心水泵为输送水的设备，根据离心水泵的相似理论，在雷诺自模区内，水泵中流体在不同转速下的状态是相似的[16]。同一台离心水泵的两个相似工况点之间满足如下关系：

式中，f为离心水泵的供电频率，Hz；n为离心水泵转速，r/min；qv为离心水泵流量，kg/s；P为离心水泵功率，kW；下标1为离心水泵工作在工频下；下标2为离心水泵工作在实际供电频率下。

通过改变叶轮转速来调节离心水泵的流量及功率是一种易于实现的节能方式，水泵的频率-流量关系及频率-功率关系可根据以下关系式进行拟合，其中A0～A2和B0～B1为拟合系数：

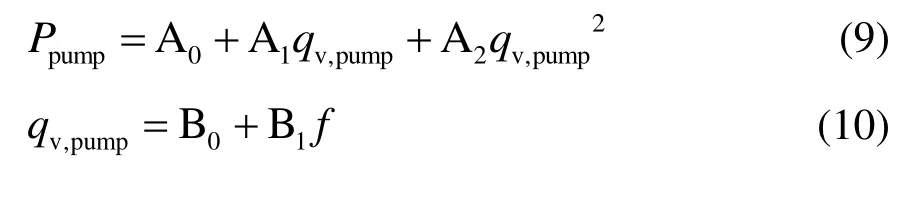
2.3 风机建模

风机是依靠输入的机械能，提高气体压力并排送气体的机械设备。与离心水泵类似，风机转速影响风机的流量和功率，风机的频率与流量关系、频率与功率关系可根据以下关系式进行拟合，C0～C2和D0～D1为拟合系数[17]。

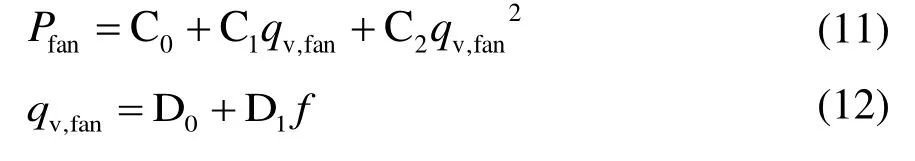
2.4 冷水机组建模

结合ASHRAE冷水机组能耗的经验模型[18]和Boruta能耗特征选择算法的结果，确定冷水机组能耗模型的建模参数为冷水机组能耗、冷负荷、冷却水进水温度及冷冻水出水温度，其余重要度值较低的特征和不重要特征选择舍弃。参照ASHRAE冷水机组能耗的经验模型，确定本文冷水机组的能耗模型表达式如下，其中E0～E5为拟合系数。

2.5 系统能耗模型及模型验证

在多冷水机组系统中，机组制冷循环产生的冷冻水输送给末端设备，机组制冷循环所产生的热量通过冷却水输送给冷却塔排放到室外空气中。冷水机组通过冷却水进出水温度和冷却塔建立关联，冷却水泵通过冷却水流量分别和机组子系统和冷却塔子系统建立关联。如式(14)所示，系统的总能耗为水泵、风机和冷水机组的能耗之和：

该多冷水机组系统配置了能源监管系统，能够对多冷水机组系统的运行数据进行实时监测与存储。本文利用该多冷水机组系统2019-08-01—2019-09-20的24 000组运行数据进行冷水机组系统的建模及验证，24 000组运行数据的冷负荷分布情况如表2所示，室外气象条件如图5所示。

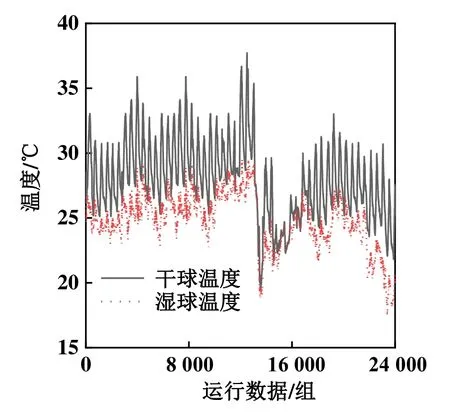
图5 室外温湿度分布

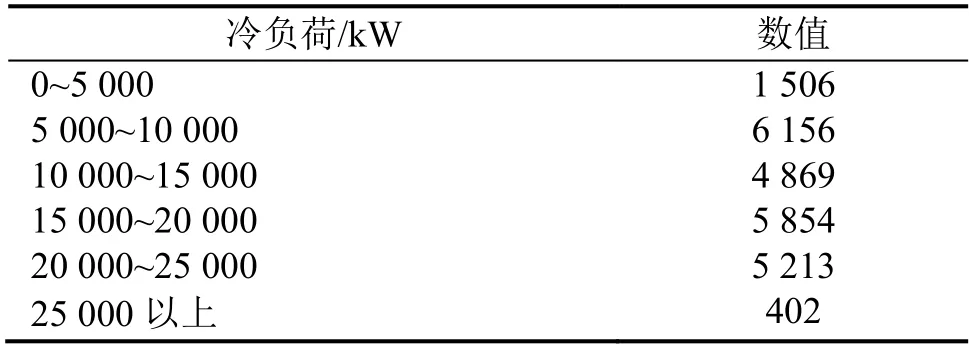
表2 冷负荷分布

在24 000组运行数据中，21 000组运行数据作为训练集用于建模训练，3 000组运行数据作为测试集用于验证模型的准确性，测试集从整个数据集中随机抽取。对比预测值与实测值的偏差是检验模型准确性的通用方法。

图6所示为测试集中400组运行数据预测值与实测值的对比。图7所示为整个测试集中预测值与实测值误差分布。由图7可知，86%的测试集运行数据的预测值与实测值的偏差小于2%。

图6 测试集系统能耗预测值与实测值对比

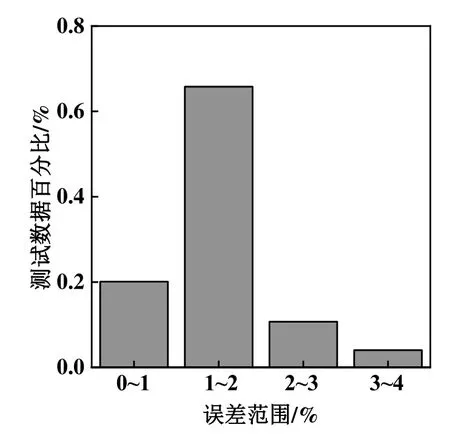
图7 测试集中预测值与实测值误差分布

为了全面量化系统能耗预测值与实测值的偏差，本文采用平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）和相关性系数（R2）作为量化指标。模型预测值和实际测量值之间MAPE和R2根据式(15)和式(16)计算，其中Pi为预测值，Mi为实测值：

MAPE越小，R2越大，说明模型预测值与实测值之间的误差越小，模型的预测准确性越高[19]。如表3所示，能耗预测模型的MAPE为1.54%，R2为0.968，说明能耗预测模型有较高的准确性。

3 基于PSO算法的优化控制策略

为了验证多冷水机组能耗预测模型的可用性，本文利用该能耗预测模型，采用基于PSO算法的优化控制策略对冷水机组系统进行优化控制，并将此优化控制策略与常规顺序启停策略进行比较。

3.1 多冷水机组系统的基本控制

多冷水机组系统的基本控制回路如图8所示，包括冷却水进水温度控制回路、冷却水进出水温差控制回路、冷水机组供水温度控制回路[20]。

图8 多冷水机组水系统控制原理

在冷却水进水温度控制回路中，控制器#1通过调整冷却塔运行风机的数量及其转速，改变冷却塔的总风量，使得冷却水的进水温度控制在设定值上；在冷却水进出水温差控制回路中，控制器#2通过调整冷却泵的运行数量及其转速，改变冷却水回路的流量，使得冷却水的进出水温差控制在设定值上；在冷水机组供水温度控制回路中，控制器#3通过调整各台冷水机组的启停状态及其所承担的负荷，改变冷水机组的供水温度，使冷冻水出水温度控制在设定值上。

3.2 基于PSO算法的优化控制策略

本文选取冷水机组冷冻水出水温度设定值、冷却水进水温度设定值以及机组负荷率作为整个系统实时优化的控制参数，冷却水进出水温差设定为6 ℃，选取冷却塔风机、冷水机组及冷却水泵总能耗最小作为优化控制策略的寻优目标，提出如图9所示的寻优控制计算流程，用以实现冷水机组系统的优化控制。

图9 粒子系统群优化算法的控制计算流程

机组优化控制问题的数学表达式如式(18)所示，约束条件如式(19)～式(22)所示：

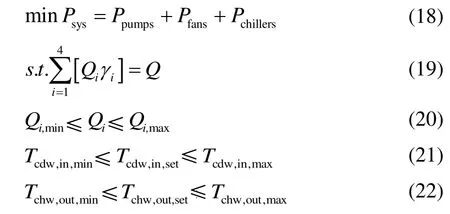
式中，Qi为第i台机组所承担的冷负荷，kW；γi为第i台机组的启停状态。0为机组关闭，1为运行。

上述优化问题可采用PSO算法求解，相关参数配置如表3所示。

表3 优化策略的PSO算法参数配置

3.3 优化策略与常规顺序启停策略的对比

为了对比验证优化策略的节能效果，本文引入了常规顺序启停策略。在常规顺序启停策略中，各台机组根据系统承担的总冷负荷按表4顺序启停，冷冻水泵随配套的机组启停，冷却泵和冷却塔的开启数目和机组开启数目相同。各运行机组的冷冻水出水温度设定为13 ℃，冷却水进水温度设定值为30 ℃，冷却水进出水温差设定值为6 ℃。

表4 冷水机组启停顺序

本文选取8月某一天作为典型日进行节能优化控制，在典型日多冷水机组系统全天24 h一直处于运行状态。图10所示为该典型日的室外干湿球温度变化，图11所示为该典型日室内冷负荷变化。

图10 典型日室湿球温度

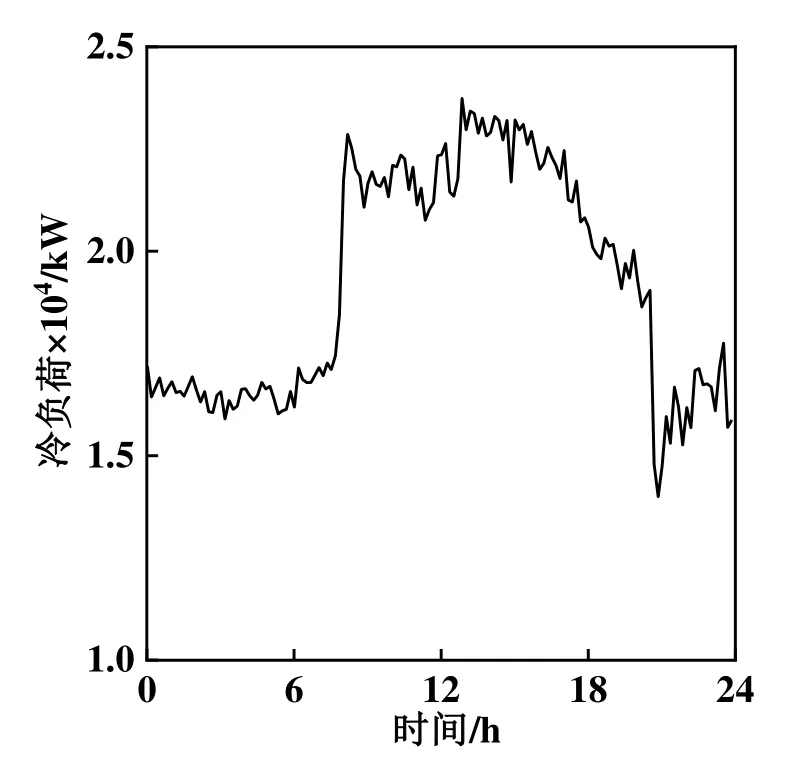
图11 典型日冷负荷

图12所示为多冷水机组系统在各策略下的逐时运行能耗，优化策略在各个时刻的运行能耗均低于常规策略。以常规策略为基准，优化策略在典型日的节能百分比为8.31%。

图12 典型日系统逐时运行能耗

4 结论

本文以某冷水机组系统为研究对象，通过对实际运行数据的数据处理和基于设备经验模型的回归拟合，建立系统的能耗预测模型。在能耗预测模型的基础上，采用基于PSO算法的优化控制策略对冷水机组系统进行优化控制，并将该策略与常规策略节能效果进行比较，得出如下结论：

1）在能耗预测模型中，86%的测试集预测值与实测值的偏差小于2%，测试集能耗预测模型的平均绝对百分比误差（MAPE）为1.54%，相关性系数（R2）为0.968，能耗预测模型在保证简洁性的基础上有较高的准确性；

2）与常规控制策略相比，基于能耗预测模型的优化控制策略在典型日的节能百分比为8.31%，验证了能耗预测模型应用于冷水机组系统优化控制中的有效性。