智能手机单点定位随机模型与平滑方式分析

葛于祥, 刘 赞, 李增科, 王阳阳, 刘冰雨

(1.中国矿业大学 自然资源部国土环境与灾害监测重点实验室,江苏 徐州 221116; 2.中国矿业大学 环境与测绘学院,江苏 徐州 221116)

0 引 言

智能手机在所有智能终端中占有极大的比重,随着社会的发展进步,智能手机用户对全球卫星导航定位系统(global navigation satellite system,GNSS)提供的位置服务有了越来越高的精度要求[1-2]。Android 7.0版本之前,谷歌公司没有开放收集Android智能手机中相位、伪距等信息的接口,研究人员无法直接从手机中获取GNSS原始观测数据,只能使用系统内部算法计算好的导航定位结果。谷歌公司在2016年举行的Google I/O会议上宣布,从Android 7.0版本开始,研究人员可以从智能手机中获取GNSS原始数据。这一举措使得开发者看清了智能手机GNSS服务的盲区,开发者可以通过智能手机中的观测数据直接或间接地得到伪距、载波、多普勒等观测值,以此进行实验和算法研究,为智能终端导航和定位精度的提高带来了无限可能[3]。

现有研究表明,处于观测条件较好的环境下,智能手机的定位精度为3～5 m[4]。当观测条件较差时,智能手机定位的精度会降到10 m或者更低[5]。智能手机相比于测量型接收机会发生频繁的信号失锁现象,且观测值更易受到多路径效应的影响;不同型号的智能手机在追踪信号和抵抗多路径干扰的能力等方面存在明显差异[6-7]。文献[8]分析了小米8智能手机的GNSS原始观测数据,与接收机相比,智能手机中伽利略卫星导航系统(Galileo satellite navigation system,GALILEO)卫星的数据质量比全球定位系统(global positioning system,GPS)卫星的数据质量好,L5/E5波段的卫星信号质量比L1/E1波段的卫星信号质量更好;文献[9]基于谷歌Nexus 9智能平板开展伪距单点定位静态实验,建立了信噪比(signal-to-noise ratio,SNR)定权模型,相比于高度角模型,定位精度提高了26%;文献[10]基于Ublox接收机进行伪距单点定位实验,选用北斗卫星导航系统(BeiDou navigation satellite system,BDS)中不同频率伪距观测值,验证了方差分量估计模型作为双频单点定位随机模型的可行性;文献[11]基于华为mate20 Pro原始GNSS观测数据,评估了动态和静态测量模式下单GPS系统,GPS/BDS联合系统的定位精度;文献[12]使用小米8智能手机GNSS原始观测数据,采用多普勒观测值平滑伪距,平滑后伪距单点定位精度明显提升;文献[13-14]利用小米8智能手机GNSS观测数据,分析了载波相位和多普勒平滑伪距2种方式对单点定位的影响,其中多普勒观测值在智能手机端伪距平滑效果更好。

为了研究智能手机的定位性能,提高定位精度,本文基于已有研究成果,从多个方面对智能手机GNSS原始观测数据进行研究分析。首先根据智能手机原始观测数据分析可见卫星数、伪距残差、精度衰减因子(dilution of precision,DOP)等信息;其次评估等权、高度角、信噪比以及Helmert方差分量估计随机模型对智能手机单点定位性能的影响;最后研究对比了原始伪距、载波相位平滑后的伪距和多普勒观测值平滑后的伪距在动态和静态环境下的定位精度。

1 随机模型

观测值的噪声水平与卫星的种类、观测值的类型等因素密切相关,而噪声的大小决定了观测值精度的高低。建立合适的随机模型给观测值定权,然后加权解算,对于提高定位性能有重要的帮助。

1.1 等权模型

模型假设同一种类型的观测值有相同的精度且互相独立。等权模型实际上是一种特殊的加权模型,即权矩阵等于单位矩阵。在实际测量环境下,电离层延迟、对流层延迟、多路径效应等误差是信号传播过程中不可避免的,它们会对观测值精度产生不同的影响,因此把所有观测值当成等精度观测是不合理的。

1.2 高度角模型

一般而言,卫星高度角越低,其观测值会受到越严重的大气延迟和多路径干扰。高度角模型是一种反映观测值和卫星高度角之间权比关系的函数模型。基于正弦函数的高度角模型可以表示为:

σ2=a2+b2/sin2(E)

(1)

其中:卫星高度角E的单位是弧度;a、b为常数。

1.3 信噪比模型

导航定位中,卫星发射信号的强度与接收机收到该信号产生的额外信号的比值用信噪比来描述,一般使用载噪功率密度比(carrier to noise power density ration,C/N0)表示信号噪声水平。信噪比在一定程度上能反映卫星信号的质量,通常情况下,信号质量和观测值的信噪比呈正相关关系,观测精度和信号质量也呈正相关关系,因此可构建如下信噪比定权模型:

(2)

其中:C为载噪比;a、b为经验参数,与卫星系统及信号的中心频率有关。

1.4 Helmert验后方差模型

本文根据卫星所属系统的不同,将观测值分为GPS、BDS 2个卫星系统,即L1、L2,其误差方程的形式如下:

(3)

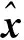
(4)

(5)

(6)

(7)

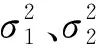
Helmert方差分量随机模型计算过程如下:

(1) 使用高度角或信噪比模型确定卫星的先验权值。

(4) 重新确定不同的观测值权值。计算公式如下:

(8)

其中,c为非零常数。

2 伪距平滑方式

多普勒平滑伪距和相位平滑伪距是2种常用的平滑方式。基于相位平滑伪距公式,借助智能手机观测值中多普勒和伪距变化率的计算关系,即可推导出智能手机多普勒观测值表示的伪距平滑公式。

2.1 载波相位平滑伪距

载波相位平滑伪距可以表示为:

(9)

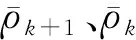
使用载波相位观测值平滑伪距时,需要满足测量设备持续锁定载波信号的条件,如果信号失锁,造成载波相位模糊度跳变,那么平滑器需重新开始[15]。

2.2 多普勒平滑伪距

欧洲全球导航卫星系统局(European global navigation satellite systems agency,GSA)在2017年发布的名为《Using GNSS raw measurements on android devices》的报告中指出,计算智能手机中的多普勒值的公式[16]为:

D=-λ/P

(10)

其中:P为伪距变化率,可以从android.location.GnssMeasurement对象的getPseudorangeRateMetersPerSecond()方法中获取;D为根据伪距变化率计算出的多普勒值。

多普勒观测值具有可持续获取、受多路径误差影响较小等优点,多普勒平滑伪距可以表示为:

(11)

(12)

其中:Δt为采样间隔;Dk+1、Dk分别为k+1、k历元的多普勒值。

3 实验与分析

3.1 数据准备

实验所需数据由华为mate30和天宝R10测量型接收机采集,实验场地在中国矿业大学南湖校区二号运动场,实验选用GPS和BDS观测数据进行研究分析,不考虑BDS2/BDS3系统间偏差的影响。

静态实验中智能手机观测时长约1 h,采样频率为1 Hz,静态定位以接收机观测数据的精密单点定位(precise point positioning,PPP)解算结果作为真值;动态实验中智能手机观测时长约30 min,采样频率为1 Hz,动态定位以接收机实时动态定位(real time kinematic,RTK)解算结果作为真值。本次实验中智能手机原始观测数据计算均使用标准单点定位算法,卫星截至高度角为15 °,截至信噪比为25 dB-Hz。

3.2 数据质量分析

华为mate30能够输出GPS、GALILEO、BDS、GLONASS以及QZSS等系统的GNSS原始观测数据,其中支持GPS的L1和L5双频信号、Galileo的E1和E5a双频信号以及QZSS的L1和L5双频信号。本文从可见卫星数、精度衰减因子、伪距残差3个方面进行智能手机和测量型接收机原始观测数据对比,简要评估了智能手机的GNSS数据质量。

3.2.1 可见卫星数

图1a、图1b所示为静态测量模式下,同一观测时段接收机和华为mate30、天宝R10可见卫星数量对比情况。任意历元下,不论是华为mate30还是天宝R10测量型接收机,BDS可见卫星数量都大于GPS卫星数量。华为mate30每个历元平均可见卫星数为37.9颗,其中BDS可见卫星数为14.3颗,GPS可见卫星数为7.2颗;天宝R10接收机可见卫星数平均为37.1颗,其中BDS为12.0颗,GPS为7.7颗。天宝R10与华为mate30的总可见卫星数相差不大,但接收机可见卫星数随历元变化更稳定,华为mate30可见卫星数起伏明显,说明华为mate30会发生频繁的卫星失锁现象,同时华为mate30采集到的GNSS原始数据还存在部分卫星载波相位信息缺失、双频观测值数量有限等问题。

3.2.2 精度衰减因子

DOP可以用来表示GPS、BDS卫星和接收机之间构成的几何图形强度,DOP会影响GNSS单点定位的精度。图1c、图1d所示为华为mate30、天宝R10精度衰减因子对比情况。从图1c、图1d可以看出,在相同观测时段和观测条件下,华为mate30相比于天宝R10,接收机几何精度衰减因子(geometric dilution of precision,GDOP)和位置精度衰减因子(position dilution of precision,PDOP)数据波动更大、更明显,卫星间的几何图形强度更不稳定;接收机的GDOP和PDOP随时间变化平缓波动,卫星间的几何图形强度相对稳定。观测时段内,华为mate30平均GDOP为1.822、PDOP为1.523;天宝R10平均GDOP为1.580、PDOP为1.351。

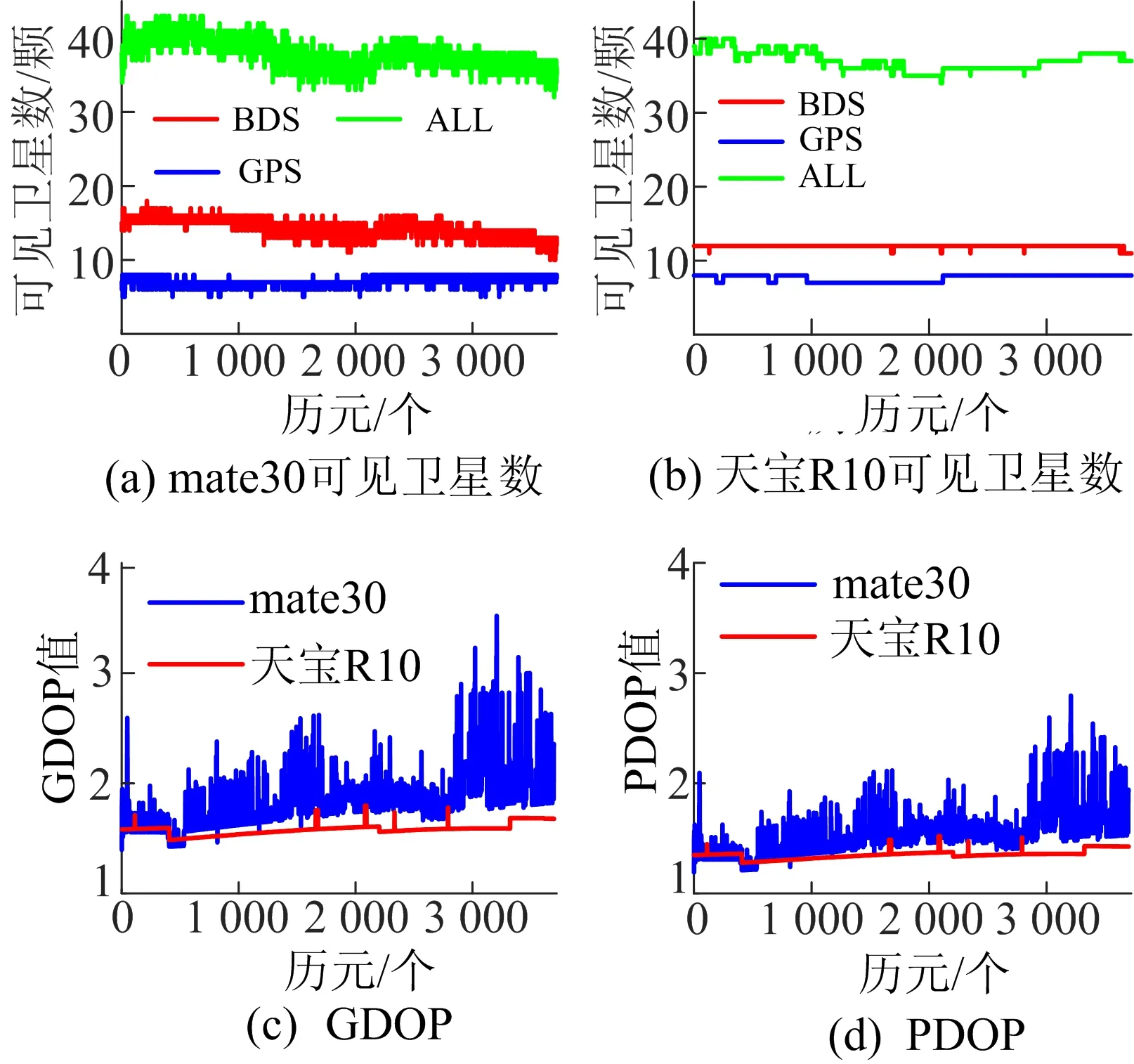
图1 华为mate30、天宝R10可见卫星数和精度衰减因子

3.2.3 伪距残差

伪距残差可以用来衡量伪距观测值质量的优劣,伪距观测值质量较好时,残差在零值附近波动。为研究华为mate30和天宝R10测量型接收机伪距残差分布情况,限于篇幅,在BDS和GPS卫星系统中分别选择2颗卫星进行对比。华为mate30和天宝R10部分卫星伪距残差如图2所示。

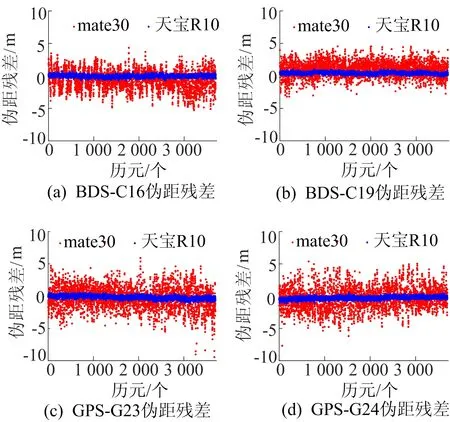
图2 华为mate30和天宝R10部分卫星伪距残差

从图2可以看出,智能手机GNSS观测数据计算出来的伪距残差波动较大,C16、C19、G23、G24的伪距残差平均值分别为-0.62、0.98、-0.29、-0.28 m;天宝R10测量型接收机伪距残差变化较为平滑,在零值附近波动,C16、C19、G23、G24的伪距残差平均值分别为-0.02、0.42、-0.27、-0.18 m。需要注意的是,BDS卫星伪距残差相对零均值有整体性偏移,考虑与BDS2/BDS3系统间偏差有关。智能手机GNSS观测值中含有较多的粗差,抵抗多路径能力远差于测量型接收机,这与手机内部构造、GNSS芯片性能以及天线位置等因素有关。

3.3 随机模型分析

为研究不同随机模型对Android智能手机单点定位的影响,本文采用等权、信噪比、高度角等先验模型和Helmert方差分量估计后验模型进行对比分析。

3种随机模型在E、N、U方向的误差对比如图3所示。

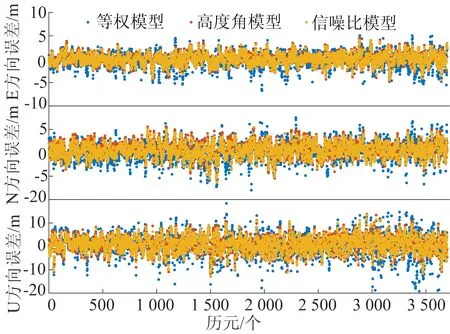
图3 3种随机模型定位精度对比

从图3可以看出,等权模型在各个方向的离散程度较大,且存在更多误差较大的点,定位结果较差;高度角模型在各个方向的定位误差离散程度小于等权模型;信噪比模型3个方向的定位效果较好,误差波动范围较小,结果相对集中。等权、高度角和信噪比模型在E、N、U方向的定位均方根误差(root mean square error,RMSE)见表1所列,其中等权模型定位精度较差,信噪比模型精度最优。

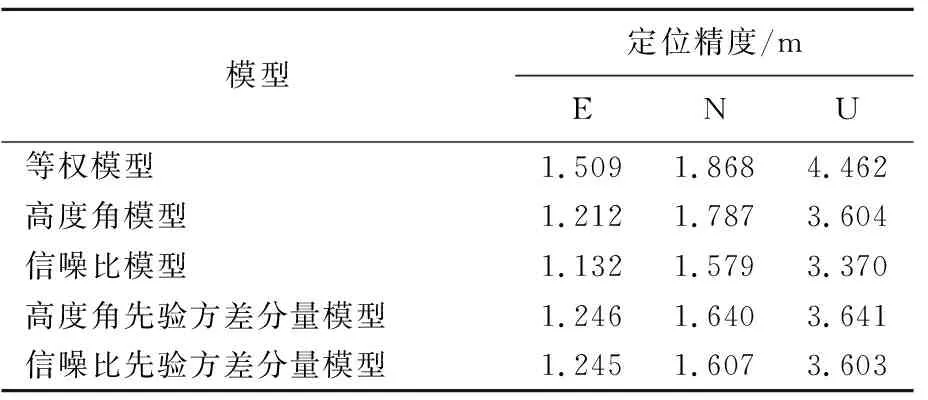
表1 不同随机模型单点定位精度对比

信噪比模型相比于高度角模型,平面定位精度提高了10%,高程方向的精度提高了6%;相比于等权模型,平面定位精度提高了19%,高程方向的精度提高了24%。

3种随机模型在水平和高程方向误差累积分布曲线如图4a、图4b所示。从图4a、图4b可以看出,在平面和高程误差累积分布中信噪比模型都更有优势,在概率相同的情况下,信噪比模型定位误差更小。以圆概率误差(circle error probable,CEP)为例,如图4c～图4e所示。从图4c～图4e可以看出，信噪比模型平面精度CEP95为3.238 m、CEP50为1.554 m;高度角模型平面精度CEP95为3.496 m、CEP50为1.678 m;等权模型平面精度CEP95为4.115 m、CEP50为1.975 m。通过对CEP的分析也可知信噪比模型更有优势。

方差分量估计随机模型在E、N、U方向上的精度对比如图5所示。

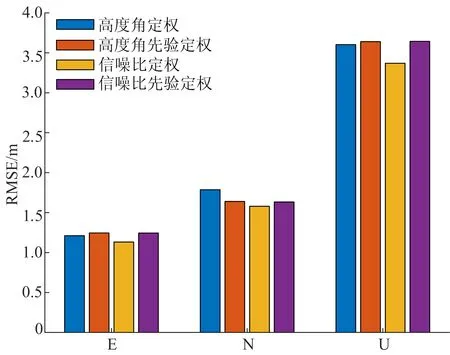
图5 方差分量随机模型定位精度对比

从图5和表1可以看出,基于高度角先验确权和信噪比先验确权的方差分量随机模型各方向定位精度大体相当,2种先验定权方法的东方向精度比仅使用高度角模型和信噪比模型都有所下降,北方向精度比仅使用高度角模型有所提升,比仅使用信噪比模型有所下降。

2种先验定权方法的平面定位精度比仅使用高度角模型的平面精度有小幅提升,但稍差于仅使用信噪比模型;在高程方向,使用信噪比模型定位精度最好。

利用测量型接收机观测到的GNSS数据进行单点定位通常使用高度角模型,本次实验使用华为mate30智能手机作为数据采集设备,发现基于信噪比模型的单点定位效果最佳,对于低成本终端来说,信噪比更能反映观测值的精度,这与前人的研究结论相同。

Helmert方差分量估计模型计算复杂,易受到粗差的干扰,但适用于不同类型、不同精度的观测值联合处理。本文在单点定位中使用方差分量随机模型,各方向定位精度相比于等权模型均有所提高,平面定位精度相比于高度角模型也有所提高,但效果有限。

3.4 伪距平滑方式分析

通过上述研究分析可知,信噪比随机模型更适用于智能手机单点定位,由此使用基于信噪比随机模型的单点定位，分析2种平滑方式在动态测量和静态测量模式下对定位精度的影响。

3.4.1 静态实验

动态和静态模式下伪距平滑方式精度对比如图6所示。

伪距平滑方式精度对比见表2所列。

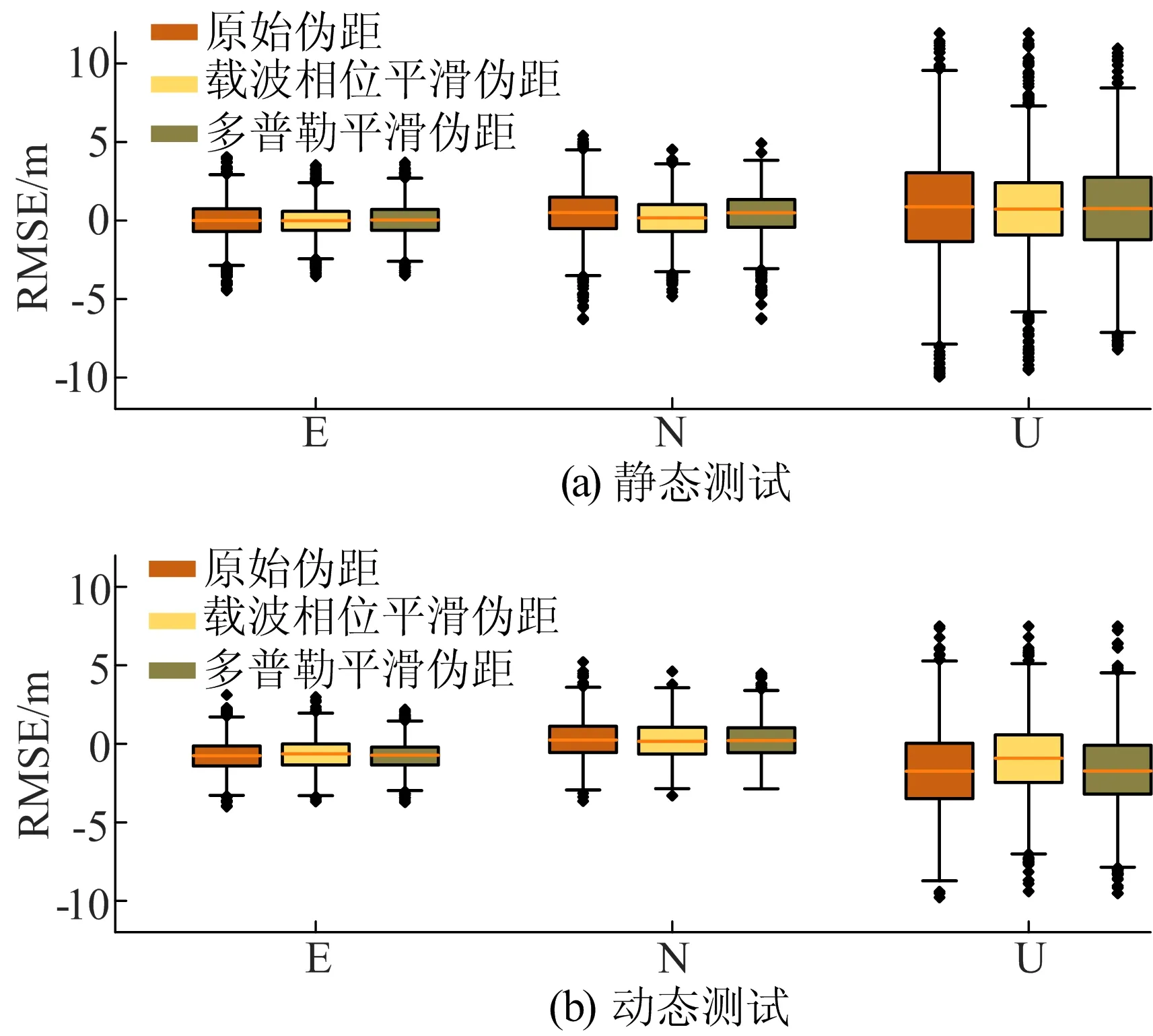
图6 动态和静态模式下伪距平滑方式精度对比

表2 伪距平滑方式精度对比

从图6a和表2可以看出,与未平滑的伪距相比,平滑后的伪距在E、N、U方向上的定位精度都有所提升,使用相位平滑的伪距比原始伪距平面定位精度提高了16%,高程方向提高了17%;使用多普勒平滑的伪距比原始伪距平面定位精度提高了10%,高程方向提高了10%。同时可以发现,载波相位平滑伪距在E、N、U方向上的定位误差更集中,原始伪距在3个方向上的定位误差相对发散。基于华为mate30原始观测数据,在静态测量模式下,2种观测值平滑伪距的方式都能提高单点定位精度,载波相位平滑伪距方式提升效果更明显。

3.4.2 动态实验

从图6b和表2可以看出,在动态测量模式下,可以得到与静态实验相同的结论,即经过2种平滑方式处理的伪距相比于未被处理的伪距都能提高定位精度。在平面定位精度方面,多普勒观测值平滑伪距方式效果较好,提高约5%;在高程定位精度方面,载波相位平滑伪距方式提升幅度较大,提升约20%。多普勒观测值平滑伪距和载波相位平滑伪距定位误差分布更加集中,稳定性更好。

单点定位主要使用伪距观测值进行计算,伪距精度的高低对定位结果的好坏起着至关重要的作用。一般而言,载波相位和多普勒观测值的精度比伪距观测值的精度高,利用这2种观测值来平滑伪距可以提高定位精度。本文基于华为mate30原始GNSS观测数据,使用载波相位和多普勒观测值平滑伪距,实验结果与前人研究结论相同,即2种平滑方式都可以提高伪距观测值的精度,精度改善程度与观测条件、观测设备等因素有关。

4 结 论

本文基于华为mate30智能手机输出的GNSS原始观测数据,研究了多种随机模型和2种伪距平滑方式对定位结果的影响,结果表明:

(1) 智能手机和接收机可见卫星数相差不大,但智能手机数据波动较大,会发生频繁的卫星失锁现象。受限于智能手机内部设计构造,智能手机抵抗多路径能力稍显不足,观测值质量较差。智能手机与测量型接收机相比,DOP更大且数据更不稳定。

(2) 相比于等权和高度角定权模型,信噪比定权模型更适用于智能手机GNSS观测数据,可以显著提高平面定位精度和高程精度。基于信噪比随机模型的单点定位,数据稳定性更好,结果更加集中。

(3) 当使用不同卫星系统的GNSS观测数据进行单点定位时,Helmert方差分量估计随机模型能够提高定位精度,但效果有限;基于高度角先验定权和信噪比先验定权的方差分量随机模型定位精度大体相当。

(4) 2种平滑方式在动态和静态测量模式下均能提高定位精度。静态实验中,使用相位观测值平滑伪距的方式定位精度提升显著;动态实验中,2种伪距平滑方式平面定位精度接近,多普勒平滑伪距的方式稍好,但相位平滑伪距在高程方向定位精度提升明显。

智能手机通常搭载成本低、体积小的线性极化天线和功耗低、性能差的GNSS芯片,这会严重影响观测数据的质量。不同型号、不同系统的智能手机搭载的芯片也不尽相同,这就导致观测到的卫星系统、信号频率、观测值类型等出现差异,会对定位结果产生不同的影响。充分利用智能手机观测数据,建立普适的高精度定位模型是下一步研究的重点。