一种应用于单光子测距的去噪算法及电路

程 帅, 刘兴辉, 赵宏亮, 赵 野, 李 博, 赵发展

(1.辽宁大学 物理学院,辽宁 沈阳 110036; 2.中国科学院 微电子研究所,北京 100029; 3.中国科学院 硅器件技术重点实验室,北京 100029)

0 引 言

近年来,应用于单光子测距电路中的时间相关单光子计数(time-correlated single-photon counting,TCSPC)技术日趋成熟[1]。因为测距系统的灵敏度很高,探测目标背景会产生很大噪声,所以有效地去除噪声是发挥单光子测距电路探测能力的关键[2-5]。

目前提出的去噪算法比较单一,本文称这类算法为传统去噪算法。在传统的去噪算法中,利用单光子在某一时间窗口具有时间相关性、而背景光往往呈均匀分布这一特性[6-8],从统计直方图中进行逐条筛选,筛选出具有一定时间间隔的相对较高的信号作为有效单光子信号,从而完成去噪[9-10],但逐条筛选的方法效率太慢。

本文提出的单光子去噪优化算法避免了逐条进行筛选,采取先进行“粗定位”而后进行“细定位”的原则对单光子进行等效筛选,从而在保证准确性和传统筛选算法一致的情况下,大幅度地提高了数据处理的效率,减少了数据处理的时间。本文不但给出了实现优选算法的数字电路结构,解释了这种结构的原理,同时也给出了一种结合该算法的单光子测距电路及其仿真结果,从而在电路层面验证了算法的有效性和正确性。

1 单光子去噪原理及测距电路

对于单光子,因为在某一时间窗口内具有时间相关性,而背景光往往随时间呈均匀分布,所以在以时间为横坐标、光子数为纵坐标的统计直方图中,单光子信号往往对应着纵坐标值相对较高的几条,可它们又不能靠得太近,靠得太近极有可能同属于一个光波信号。因此筛选单光子信号的原则如下：在对应的统计直方图中找到纵坐标值较高而相距较远的若干条,它们被视为单光子信号。

单光子信号在时间窗口里的时间相关性如图1所示,在这里单光子都聚积在某一时间窗口内,而背景光没有这种聚积性,随时间均匀分布。因此在这些时间段的光子数明显多于其他时间段收集到的光子数,而去噪工作正是找到这些时间段以及它们对应的光子数。在进行多次统计后,可生成以时间相关光子数为纵坐标、时间为横坐标的时间光子数统计直方图。单光子的去噪过程实际上就是在该直方图中筛选出光子数最多且相隔一定时间的几条,这些条的横坐标所对应的时刻即为单光子信号的到来时刻。本文在1 024个数据的直方图上进行筛选,筛选出3个单光子信号。

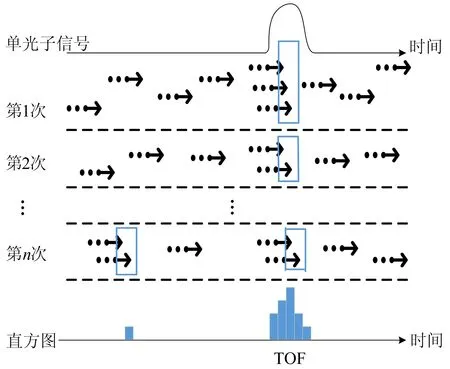
图1 相关单光子探测原理图

单光子测距主要利用统计直方图找出单光子的到来时刻,再结合已被测量的单光子发射时刻,两者做差乘光速的1/2得出被测目标距离信息。因此测距的关键在于单光子去噪,找出单光子到来时刻即可完成测距。

整个测距系统分为光子探测部分、相关光子探测电路、光子计数模块、时间数字转换器以及数字信号处理电路。光子探测部分的作用是将一个光子的光脉冲信号转变成具有一定持续时间的方波信号,并将这些信号送入时间相关光子探测电路中。时间相关光子探测电路根据是否有2个或以上的光子方波的上升沿聚集在时间窗口内来决定trigger信号是否为1,并将trigger信号分别送入时间数字转换器以及光子计数模块中。时间数字转换器将trigger信号到来时刻测量出来并以二进制数字的形式输出,光子计数模块则将时间窗口内的光子数全部计入。接下来,将时间数字转换器的测量结果以及对应光子数送入直方图获取电路中生成以时刻为横轴、光子数为纵轴的时间光子数统计直方图。最后送入数字信号处理电路中进行单光子去噪,本文着重介绍这一部分的改进及优化。

2 优化的去噪算法

本文所提出的单光子去噪算法是对传统去噪算法的优化。相比于传统算法对单光子统计直方图的逐条筛选,本文提出的优化算法则是首先确定单光子的一个比较大的时间范围,也就是确定在统计直方图的某16条内,当确定这个范围后,然后在选好的这些16条中进行细筛选,并最终确定单光子所在的位置。

2.1 传统的单光子去噪算法

传统的单光子去噪算法是指对光子数统计直方图进行逐条比较,直至将直方图的所有条全部比较完为止。但传统的去噪算法需要对直方图的所有条都进行一次对比,这里以1 024条为例,通过对这1 024条进行逐条对比，从中筛选出纵值最高且相距至少16条远的3条代表3个单光子信号。因为这种筛选方式严重地拖慢了算法的运行速度,所以对算法的优化十分必要。

2.2 单光子去噪的优化算法

为了避免数据的多次比对和判断,本文提出了一种优化的去噪算法。优化算法要经过先粗去噪再细去噪2个步骤。粗去噪是指将1 024个数据按序存入32阶的二维方阵中,其中将每16个光子数作为一组数据在直方图的先后顺序编入一个4阶分块矩阵中,并用有序整数对(row, col)(row,col在0～7之间,row称为行,col称为列)为其进行编号。因此整个矩阵被分成64块,具体的数据存储结构如图2所示。

图2 数据存储结构

在对某一分块矩阵的16个位置存满后则进行求和再进行逐块筛选。具体过程是从编号为(0,0)的矩阵开始,将该分块矩阵中的16个数据进行求和。之后列进行递增加1,求和后与前一块矩阵数据和进行比较。当某块列为7时则跳转下一行,直至比较到(7,7)为止。此处将当前矩阵块的数据和记为r,编号记为(row,col)。在此过程中若某块的和最高,则将其和定为r1,编号定为(rowt1,colt1)。(rowt2,colt2)有2种产生方式:① 找到与(rowt1,colt1)相差超过一列(下文称为条件1,若换成(rowt2,colt2)则称条件2)的块将其和定为r2,将其序号暂定为(rowt2,colt2)。若在比较过程中发现满足条件1且和超过r2的块,则将该块序号定为(rowt2,colt2)。② 发现某块和超过r1且满足条件1,则将原(rowt1,colt1)定为(rowt2,colt2)。(rowt3,colt3)的产生方式有如下3种:① 将同时满足条件1、条件2的块的和定为r3,序号暂定为(rowt3,colt3),在比较过程中若某块和超过r3且满足条件1、条件2,则将其序号定为(rowt3,colt3);② 若某块和超过r2且满足条件1、条件2,则将原(rowt2,colt2)定为(rowt3,colt3);③ 若某块和超过r1且满足条件1,则将原(rowt2,colt2)定为(rowt3,colt3)。优化算法粗去噪的具体流程如图3所示。

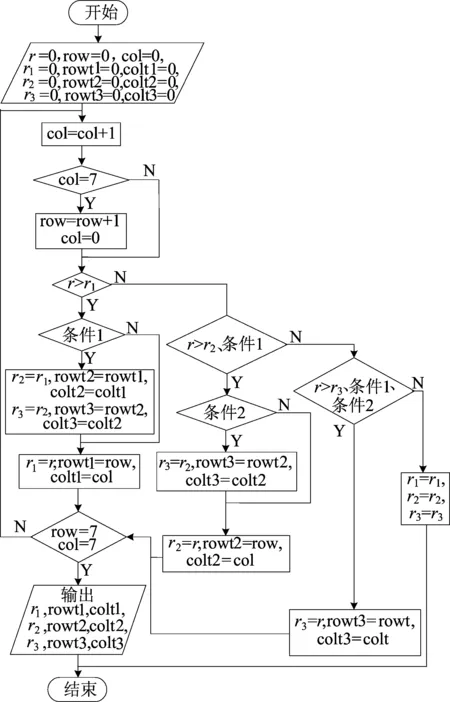
图3 优化算法粗去噪流程

由图3可知,经过这样的流程找出的3个分块矩阵中一定存在需被筛选出的3个单光子信号,且每个分块矩阵中各自存在一个。这是由于2个单光子信号至少需要隔开16条的距离,可一个分块矩阵中的距离必小于16条,因此一块中不可能存在2个单光子信号。而依照该选取原则所筛选出的是数据和最高的且相距至少一列的3块,数据和最高意味着波峰的位置就在这些块中,相隔至少一列保证了它们至少相隔16条远,因此3个单光子信号分别在这筛选出的3个分块矩阵中。若想确定它们的具体位置,则需进行下面的细去噪过程。

细去噪过程指的是从已经选好的3个分块矩阵中确定出3个单光子信号的位置。具体原则是从筛选好的3块中分别进行按条筛选并确定出光子数最大的一条。具体流程是从第1条开始与后一条进行对比,留下较大的条,直至比到最后一条(第16条)。每一块都进行这样的筛选,最终确定的3条即为3个单光子信号在对应矩阵中的位置hisfinet1、hisfinet2、hisfinet3。最后,将细筛选所确定的条数再加上128倍的相应矩阵块的行数与16倍的列数之和所得到的数,就对应着3个单光子信号在时间光子数统计直方图上的位置TOF1、TOF2、TOF3。

2.3 传统算法与优化算法的对比

对比文献[9]传统算法的逐条筛选机制,本文的优化算法在保证准确度的同时具有更高的效率。2种算法的筛选机制的对比示意图如图4所示。

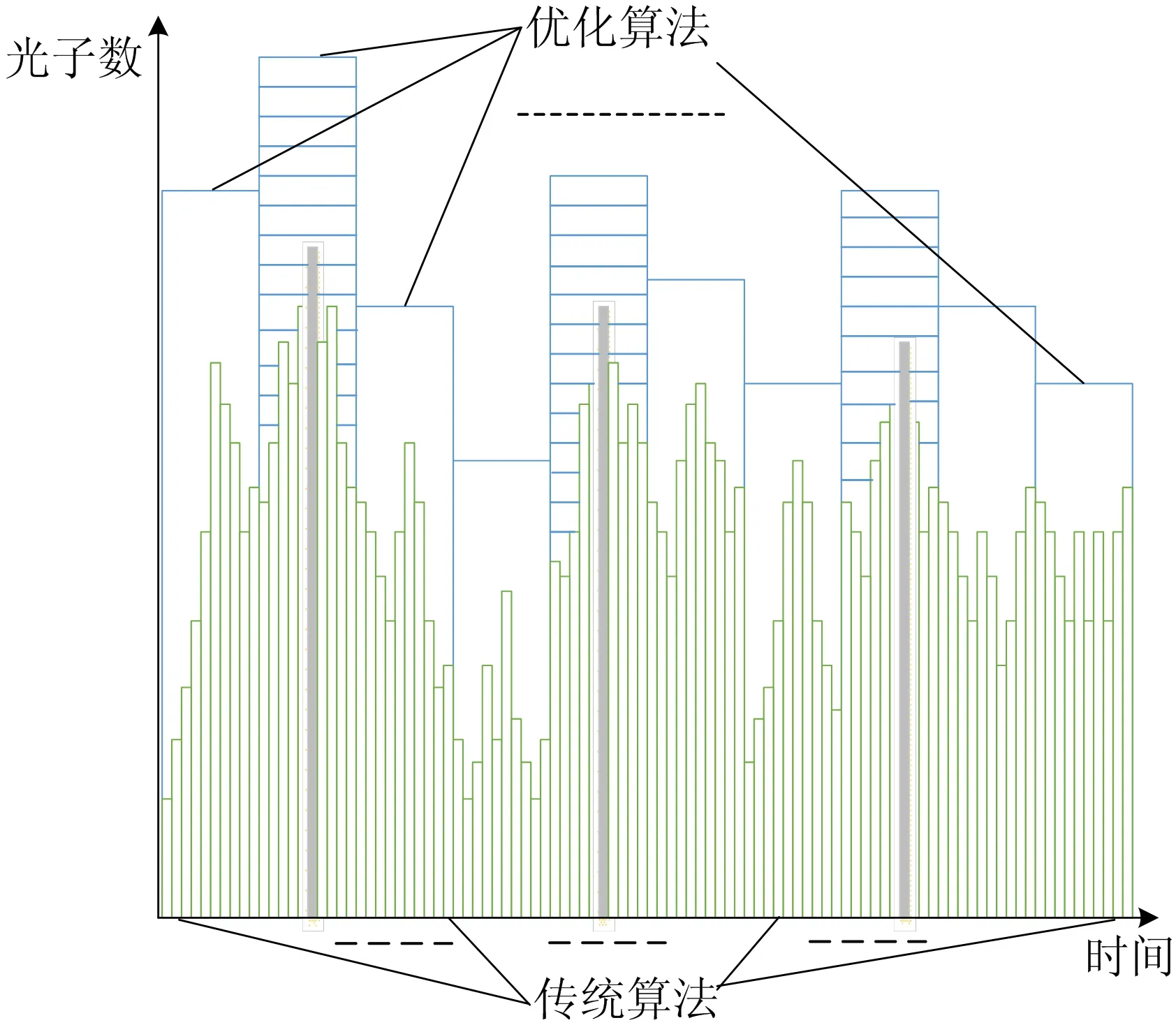
图4 2种算法筛选机制对比示意图

从图4可以看出,传统算法为将图4中的细条进行逐条对比判断,从而筛选出3个用实心细条表示的TOF1、TOF2、TOF3。而优化算法则是将细条分组作和(用粗条代表),先进行64个和的对比和判断,筛选出3个用带有阴影的粗条表示的“粗略位置”,再在这3个“粗略位置”中经细筛选找出与传统算法找出的相同的3条。

由以上分析可知,算法的数据规模大大缩减。传统的去噪算法有1 024个数据,本文提出的优化算法只需要对比112个数据。而若从算法运行次数的角度上看,传统算法需运行1 023次,而优化算法只需运行108次。结合每个算法运行时所需步数可以看到,传统算法需运行11 253步,优化算法只需运行1 044步。而两者所筛选的结果相同,从而保证了优化算法在精度与传统算法一致的前提下,效率超过了传统算法的10倍。具体指标对比见表1所列。

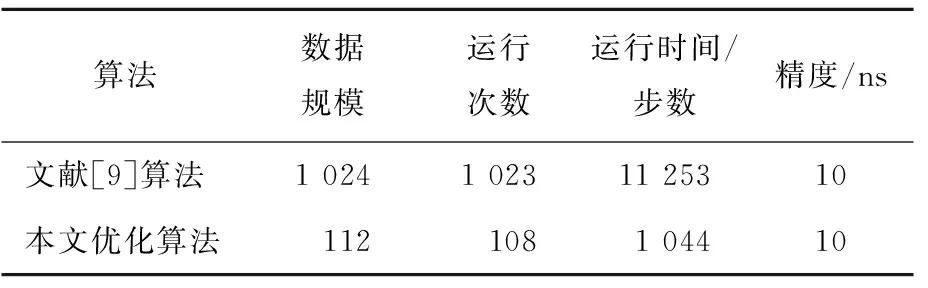
表1 2种算法指标对比

3 关键电路与仿真

本节将给出实现优化算法的数字电路的结构图及其的版图和后仿波形,用仿真数据及波形从电路层面进一步说明算法的正确性。

3.1 去噪算法核心电路

按照优化算法的流程,并结合该算法的结构,本文给出了实现此算法的电路结构,如图5所示。

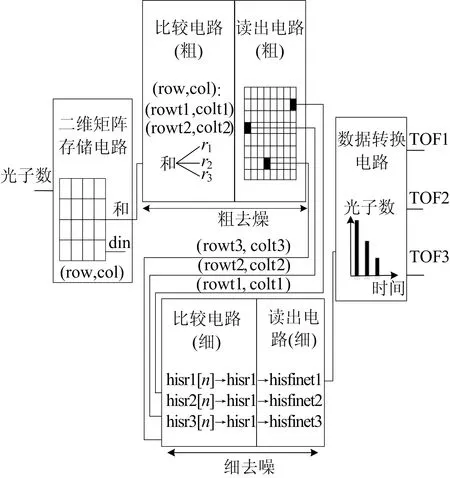
图5 去噪算法电路结构

从图5可以看出,当光子数被记下后就被送入二维矩阵存储电路中进行按块存储。接下来,每当某块数据被存满后进行作和送至粗比较电路中进行比较,直至每块都存满后将输出的(rowt1,colt1)、(rowt2,colt2)、(rowt3,colt3)送至细比较电路中。

细比较电路将这3块内的数据分别进行比较,经细读出电路选出单光子信号在这3个矩阵中的位置。最后经数据转换电路将所确定的位置转换成对应时间与光子数统计直方图上的位置TOF1、TOF2、TOF3。

3.2 版图及后仿结果

本文给出噪声去除算法电路的布局和后仿真结果,如图6所示。

从图6a可以看出,版图面积为601×1 202 μm2,电路总功耗为12.96 mW;从图6b可以看出,TOF1的位置应为00001000100,TOF2的位置应为01001001111,TOF3的位置应为01101001011。而后仿结果正是如此,这说明此电路实现了优化算法的功能,并在统计直方图中提取TOF1、TOF2、TOF3的正确位置以完成噪声去除。

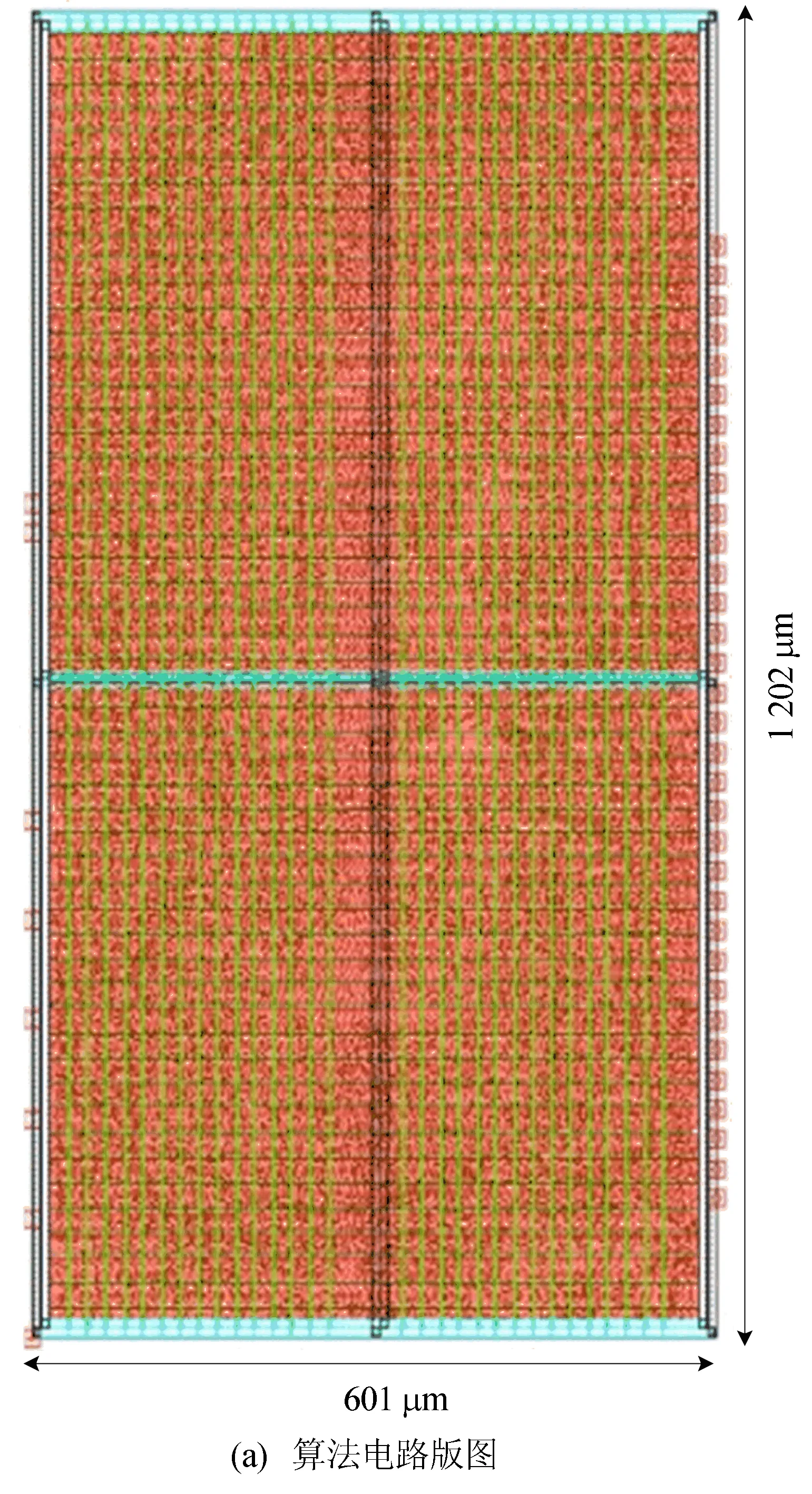
图6 算法电路版图和后仿结果

4 结 论

随着高级驾驶员辅助系统(advanced driver assistance systems,ADAS)中对高分辨率光检测和测距(light detection and ranging,LIDAR)技术的需求越来越高,本文引入了一种应用于激光测距的去噪算法,该算法可以执行与时间相关的单光子测距和完整的数字信号处理电路，它包括粗过滤和细过滤2个过程。在粗滤波中,将每个16个光子作为一个组,并首先编为4×4子阵列,在子阵列块中,将汇总所有光子,然后逐块进行筛选。在细滤波中,对来自在粗滤波中选择的3个子阵列中的每个子阵列的16个数据进行卷积,然后通过在每个子阵列中逐个地滤波来确定最大数量的光子。

本文能够根据时空相关事件生成精确触发的关键电路。仿真实验结果表明,本文提出的方法大大提高了运算速度,同时精度仍然很高,可用于激光雷达芯片的实时信号处理。