二氧化碳喷射器的喷射系数理论研究

冯小桃, 刘向农, 李鹏程, 毕笑维, 何睿祺, 刘如佳

(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)

喷射器是一种能提高引射流体的压力而不直接消耗机械能的装置,具有无运动部件、能效高和维护方便等特点,通过缩放喷嘴,工作流体的压力势能或热能转换为动能,以超音速的速度进入引射室,将压力较低的引射流体卷入混合室,发生混合后逐渐均匀,混合流体流经扩压室,动能转化为势能或热能,混合流体压力提高,并高于进入引射室时引射流体的压力[1]。喷射器作为喷射制冷的主要或辅助设备,可代替压缩机降低高品位能量的消耗,提升系统的能量利用效率[2]。喷射器的相关理论在不断创新与完善,并广泛用于制冷领域和其他行业[3]。

流体在喷射器内流动时,工作流体和引射流体的混合过程非常复杂,而实际气体的流动过程更为复杂多变。文献[4]对喷射器内实际气体的状态方程进行了深入的研究,建立了基于真实气体的气体动力学函数式,并与索科洛夫的设计方法进行了对比,结果表明,工作流体压力超过5 MPa时,索科洛夫的设计方法已出现偏差,随着压力的增大,误差也在扩大;文献[5]引入临界圆的概念,即当喷射器处于临界模式时,在引射室内工作流体与引射流体的混合薄层处,达到音速的环状区域为临界圆,并采用二维速度分布函数展示引射流体的速度分布情况,建立了一种基于理想气体的临界圆数学模型,实验验证该模型具有可行性,可以用于指导数学模型的构建。二氧化碳是一种安全无毒不可燃的自然制冷工质,廉价易得且不会危害环境。二氧化碳的热力性质十分优秀,单位容积制冷量是常规制冷剂的5～8倍,化学性质稳定,压缩机的容积效率更高[6]。相较于其他制冷剂,跨临界二氧化碳制冷系统中冷凝压力与蒸发压力较高,制冷循环过程中会出现明显的膨胀损失,而引入喷射器参与制冷循环，可以降低膨胀损失,减少压缩机耗功,提升系统的制冷效率[7]。

现有的喷射器设计方法都是基于一维模型和二维模型,但在使用二维模型的同时,对实际气体的流动过程没有深入探讨,不能准确地表达真实气体的实际流动过程。本文采用二氧化碳制冷工质,构建一种基于实际气体的二维喷射器喷射系数计算模型,并与实验测试数据进行对比,验证本文提出的计算模型的可信性。

1 含有喷射器的制冷系统概述

喷射器作为制冷系统的辅助装置,其工作性能影响着整个系统的制冷效率。喷射器结构如图1所示。

进入喷射器的工作流体来自于冷却器,此时处于高温高压低速流动状态,在喷嘴喉部达到临界速度。工作流体经过缩放喷嘴后,压力和温度降低,速度达到超音速。工作流体进入引射室后,流道突然扩大,流体在喷嘴出口过流断面和混合室入口过流断面之间流动时,产生局部损失。考虑到2个断面之间距离很小,可以忽略沿程损失[8]。由于压差的存在,工作流体与引射流体之间产生一个很薄的波阵面,超音速气流受到阻滞,来自于蒸发器的低温低压引射流体受到突跃式的压缩,形成集中的强扰动。这时出现一个压缩过程的界面,即激波。经过激波,引射流体的压强、密度和温度均升高[9]。进入混合室后,工作流体与引射流流体在混合室内进行能量交换,速度渐渐达到一致,在扩压室内混合流体开始膨胀,动能转换为势能或热能,混合流体压力提升,并高于引射流体初始压力。

图1 喷射器结构及流场示意图

含喷射器的制冷循环如图2所示。扩压室出口为气液混合物,进入气液分离器后气相流体进入压缩机压缩后进入冷却器,经过冷却再次进入喷射器,即这部分流体为工作流体;另一部分通过节流装置进入蒸发器参与制冷,蒸发后的流体即为引射流体,构成完整的制冷循环。

图2 含喷射器的制冷循环

喷射器的设计通常是以临界工况为参考,此时喷射器的喷射系数最大。本文的计算模型研究基于临界工况下的喷射器,也可适用于次临界工况的喷射器设计。

2 喷射器数学模型的构建

2.1 实际气体的热力学一般关系式

探寻实际气体在喷射器内各热力参数之间的关系,最重要的是找出实际气体与理想气体之间的偏差,选择合适的状态方程。RKS(Redlich-Kwong-Soave)状态方程较为简易,并且具有良好的计算精度,用压缩因子Z将RKS方程代换后,公式[10]如下:

Z3-Z2+(A-B-B2)Z-AB=0

(1)

(2)

(3)

(4)

a=acα(T)

(5)

b=0.086 64RTc/pc

(6)

(7)

(8)

m=0.480+1.574ω-0.176ω2

(9)

Tr=T/Tc

(10)

取温度与压力为独立变量,导数压缩因子为:

(11)

(12)

温度等熵指数kT和容积等熵指数kv的计算方程[8]如下:

kT=(1-RZT/cp)-1

(13)

(14)

在压力超过5 MPa后,二氧化碳分子间色散力的作用已不可忽略,基于理想气体的喷射器设计方法已逐渐产生误差,采用实际气体的修正方法可覆盖低压与高压工况,设计结果与实际情况之间偏离更小[4]。实际气体在喷射器内等熵流动,压力、比容和温度的关系式[11]如下:

(15)

其中:p为压力;C为常数;R为普适气体常数,R=8.314 kJ/(kmol·K);T为温度;v为比容;pc为临界压力,即7.382 MPa;Tc为临界温度,即304.21 K;ω为偏心因子,ω=0.225;kT为温度绝热指数;kv为容积绝热指数;Z为压缩因子;ZT、Zp为导数压缩因子。

2.2 条件假设

为了简化喷射器内流动过程特征而又不失准确性,做以下假设:

(1) 喷射器内部流体稳态、等熵流动,喷射器入口参数不产生波动。

(2) 工作流体与混合流体在喷射器内流动均与内壁不传热。

(3) 工作流体速度、压力与温度径向均匀分布,引射流体在混合室入口前压力、温度均匀分布。

(4) 工作流体与引射流体在临界圆混合处等温。

2.3 模型控制方程

2.3.1 工作流体进入混合室前的控制方程

工作流体的临界点速度关系到质量流量的计算以及临界圆的确定,是构建实际气体临界圆模型的关键。

文献[4]推导出真实气体的气体动力学函数理论式,得到的临界点速度控制方程如下:

(16)

其中:p0为工作流体滞止压力;v0为工作流体滞止比容。

真实气体在临界点等熵流动的相对密度关系式[4]为:

(17)

由连续性方程结合质量流量定义,代入临界状态速度与压力,工作流体质量流量方程为:

(18)

其中:A1为喷嘴喉部面积;vw,1为临界点工作流体比容;n为临界状态与滞止状态压缩因子比值。

根据等熵流动方程、能量守恒方程与连续性方程,工作流体在临界圆处满足以下控制方程:

(19)

(20)

其中:Te,0为引射流体进口温度;Tw,0为工作流体进口温度;pw,0为工作流体进口压力;pw,2为工作流体临界圆处压力;ωw,0为工作流体进口速度;ωw,2为工作流体临界圆处速度;Tw,2为工作流体进口温度;A为临界圆面积。

结合方程(17)、(18)和假设(4),得到混合室入口工作流体速度表达式为:

(21)

声速传播为绝热过程,工作流体在混合区入口处的马赫数计算公式[5]为:

(22)

结合方程(19)～(22),引入流动损失系数ξ,混合室入口工作流体实际流动直径,即临界圆直径为:

(23)

2.3.2 引射流体参数方程

在引射室内,激波的出现使得流动过程更为复杂,引射流体在引射室内的某个位置能达到音速,此处即为临界圆。引射流体的黏性作用,会在混合室内壁形成速度边界层。工作流体与引射流体界面之间,由于流动速度存在差值,将产生一个渐变的速度场,引射流体的速度场沿径向具有较大的不均匀性,靠近壁面的流体速度较小,而靠近工作流体一侧的引射流体速度接近于工作流体的速度。

为了减小误差,径向速度均匀分布的方法只适合工作流体,不能用于引射流体。

临界圆径向速度分布如图3所示。其中：R为临界圆半径；R3为此处流道半径，即喷射器的混合段半径。

图3 本文模型与其他模型速度分布对比

相较于采用传统的一维模型,采用本文模型,通过二维速度方程描述流体在混合室入口的速度分布特征更加精确,即

ω=

(24)

在临界圆截面处,根据马赫数的定义,考虑到工作流体与引射流体混合处仅为一个薄层,且2股流体接触充分,引射流体的二维速度函数指数[5]为:

(25)

引射流体的质量流量可用如下积分关系式表示:

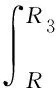
(26)

其中,ωe,2为引射流体在混合室入口处速度。

积分可得引射流体的质量流量为:

(27)

2.3.3 混合流体参数方程

在圆柱混合室入口前临界圆处,可以假定进入混合室的流体是由2股共轴流体组成。进入混合室后,2股流体发生能量交换,工作流体速度降低而引射流体速度增大,在速度趋向混合均匀的过程中伴随着引射流体的压力提升。在混合室出口,混合流体具有平均速度与静压。

根据动量定理,工作流体与引射流体在混合室进出口之间应满足的方程[1]如下:

mwωw,2+meωe,0-(mw,2+me)ω3=

(28)

混合流体进入扩散室开始膨胀,速度开始降低,压力提高,同时产生喷射器内的第2次激波。根据能量守恒定律,内部流体满足的控制方程[1]如下:

mwcpw,0Tw,0+mecpe,0Te,0=mmcpmTm+Eloss

(29)

其中:mm为混合流体的质量流量;cpm为混合流体定压比热容;Tm为混合流体出口温度;Eloss为工作流体与引射流体混合时的撞击损失,即

(30)

撞击损失同混合之前的工作流体与引射流体速度差的平方成正比,适当加大引射流体速度可减少撞击损失。此处的撞击损失虽然使得实际喷射器的喷射系数减小,并且小于理想喷射器的喷射系数,但混合流体的单位工作能力增强。

结合以上方程,得到喷射器可能达到的喷射系数计算公式为:

(31)

3 理论计算与实验数据的对比

方程(16)～(31)构成了喷射系数的理论计算模型。对于处在临界工况的喷射器,给定喷射器的结构尺寸、工作流体和引射流体的进口参数,便可求解工作流体的喷嘴喉部速度与质量流量、引射流体的质量流量、喷射系数。

喷射器结构尺寸采用文献[12]参数,关键尺寸见表1所列。

表1 喷射器结构尺寸

根据文献[12]中的实验数据,对比理想气体模型和本文计算模型,工作流体压力pw、工作流体温度Tw、喷射系数实验值u、采用本文模型的喷射系数计算值u1及相对误差δ1、采用理想气体模型的喷射系数计算值u2及相对误差δ2见表2所列。

根据表2中数据,绘制不同工况下喷射系数的折线图,如图4所示。

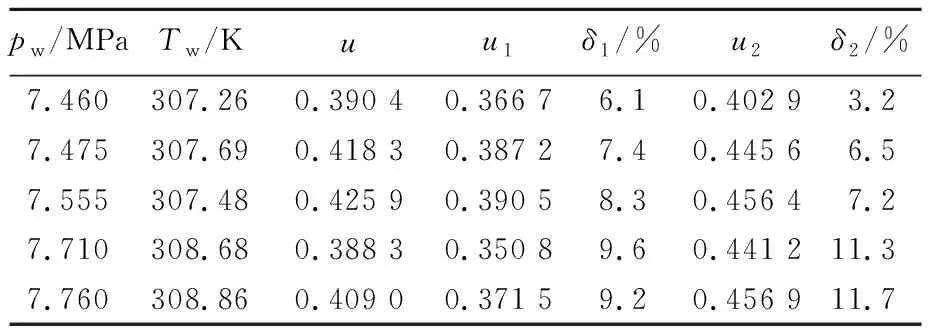
表2 不同压力下的喷射系数

图4 不同工况下喷射系数的实验值与计算值对比

由图4可知:工作流体压力为7.460、7.475、7.555、7.710、7.760 MPa时,采用本文模型所计算出的喷射系数分别为0.366 7、0.387 2、0.390 5、0.350 8、0.371 5,相对误差分别为6.1%、7.4%、8.3%、9.6%、9.2%，采用理想气体计算出来的喷射系数分别为0.402 9、0.445 6、0.456 4、0.441 2、0.456 9,相对误差分别为3.2%、6.5%、7.2%、11.3%、11.7%;同时,随着工作流体压力增大,本文模型和理想气体模型计算出的喷射系数与实际喷射系数变化趋势相似。

4 结 论

本文选取了5组工况,通过理论计算,得到了理想气体与实际气体在不同工况下的喷射系数和相对误差。

(1) 本文提出的模型理论计算喷射系数与实际喷射系数变化趋势一致,最大相对误差为9.6%,最小相对误差为6.1%,验证了本文模型具有一定的可信度。

(2) 在高压工况下,采用理想气体计算的喷射系数数值偏大,随着工作流体的压力提升,相对误差从3.2%增长到11.7%。本文模型计算值虽然偏低,但是相对误差波动较小(6.1%～9.6%),比较稳定,更适合用于高压工况下的喷射器研究。

(3) 本文模型可以用于计算工作流和引射流的质量流量和喷射系数,指导喷射器结构优化,为计算流体动力学模拟仿真提供理论基础。