基于乘客超越行为建模的航空登机效率分析
马剑,廖伟屹,陈娟,王巧,唐铁桥,原志路
(1.西南交通大学,a.交通运输与物流学院,b.地球科学与环境工程学院,成都 610031;2.北京航空航天大学,交通科学与工程学院,北京 100191;3.深圳大学,智慧城市研究院,广东深圳 518060)
0 引言
航空运输作为远距离运输的重要方式,具有快速、机动、成本高的特点。2019年,全球民用航空客运量已接近4亿人次,中国航空公司2017年搭载的旅客数量比35年前多出140 倍。客运量的飞速增长造成航空运输成本成倍增加,其中延误成本高达每年290 亿美元[1]。延误原因包括机械故障、天气恶劣、航空周转时间过长。航空周转过程中耗时最长的是乘客登机过程[2],且伴随乘客行李增多、乘客对航空服务要求提高[3],乘客登机时间(以A319、B737为例)已长达30 min[1]。因此,多年来研究学者的关键目标是优化乘客登机过程,进而缩短乘客登机时间。
运筹优化方面研究的主要目的是通过优化管理手段、策略算法等,为航空公司设计并提供更行之有效的登机策略,以实现航空公司损耗成本最小化与乘客登机效率最大化的双赢目标[4]。2008年Steffen[5]提出的优化方法是:乘客从靠窗经中间位置再到过道,每隔12 个座位(2 排)由后往前登机。而后Milne 等[6]在Steffen 策略的基础上,提出行李数量均匀分配到各排,继而分配到每排各座位,最终乘客遵循Steffen策略登机。基于座位分配思想,Milne通过建立混合整数规划模型(MILP)进一步证实增设停机坪巴士的数量也可提高登机效率[7]。实际上,早在Bazargan 的研究中,就已实现通过混合整数模型来最小化登机方案的登机延误[8]。
建立能够精确描述实际乘客登机过程的登机模型是保证研究可靠的关键。通过建立乘客登机微观行为模型模拟登机过程的研究方法近年来受到研究人员的广泛关注。Notomista 等[9]为乘客引入敏捷度系数与携带行李系数,刻画Steffen策略中乘客登机群体与个体差异。唐铁桥等[10]考虑群体行为与行李数量两种重要因素,建立行人跟随模型仿真登机过程。强生杰等[11]通过元胞自动机模拟乘客登机过程,赋予个体速度变化的规则和阈值,设计了不同登机时间间隔,又将登机仿真模型嵌入模拟退火算法中,求解出具有最小登机时间的乘客登机序列[12]。同样也有基于社会力模型、几何模型、模糊逻辑模型的建模与仿真,模拟出更为复杂、紧急的情况。Schultz[13]将考虑乘客行为和运营约束的登机模型应用于不同登机场景,并展示了侧滑式座椅额外缩短登机时间的优势。Gwynne等[14]聚焦于登机时小规模乘客的微行为(使用厕所、系安全带等),将登机过程细化到具体动作。用干扰时间和干扰次数表征总登机时间也是学者常用的方法,任新惠等[15]在干扰时间阈值的基础上求解出不同行李数量比例下的动态登机策略,并组织现场实验验证了模型的可行性。
以往研究的模型多假设客舱过道内仅允许乘客保持单列行走,忽视乘客侧身超越这一特殊行为。实际上,根据民航法规CCAR25.815 规定:大于20座的民用航空飞机客舱(如A30、A321)的过道宽度必须在20 英寸(508 mm)以上。乘客按单列依次登机时,客舱通道将会形成较长的阻塞队列,而阻塞队列的两侧会留有空隙。事实上,乘客在登机过道中经常采用侧身从空隙超越的情况,从而摆脱阻塞,降低登机过程中阻塞不前的时间占比。但是,乘客超越行为对不同登机策略实际登机效率的影响缺乏研究。
本文将通过建立考虑超越行为的登机模型重新刻画乘客登机过程,并基于不同登机策略下乘客登机过程的仿真结果,研究不同登机情景下各登机策略的效率表现,最终得出相应结论与建议。
1 考虑超越行为的乘客登机模型
本文研究的登机过程为从第1 名乘客进入单通道窄体机经济舱的入口开始,到最后一名乘客落座结束,不考虑通过休息室、检票口到舱门的过程。实际上,乘客从进入经济舱入口到落座会经历3个过程:过道中行走、放置行李、等待让座并进入座位。因此,首先分析登机时间的组成,然后考虑乘客携带行李的特征,构建乘客运动速度模型和乘客超越行为模型,最终通过模型计算乘客登机时间。
1.1 登机时间分析
乘客的登机时间为
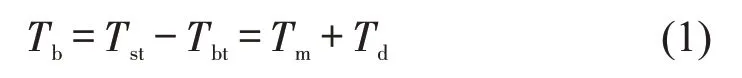
式中:Tst、Tbt分别为乘客落座时间、乘客登机开始(进入经济舱入口)时间,Tm、Td分别为行走时间、干扰延误时间,干扰延误时间又可细分为行走干扰延误时间Tmd、行李干扰延误时间Tld、座位干扰延误时间Tsd,即

式中:Tmd为乘客因为在过道行走过程中前方阻塞不前(可能是前方乘客正放置行李或是前方乘客等待更前方的乘客放置行李)而延误的时间;Tld为乘客在其座位对应的行李架前放置行李所延误的时间;Tsd为当靠过道(中间)的座位已有乘客落座时,座位在中间和靠窗(靠窗)的乘客要落座,因靠过道和中间座位上的乘客起身让行产生的时间。
参考尚华艳等[16]的行李干扰模型,行李干扰延误为
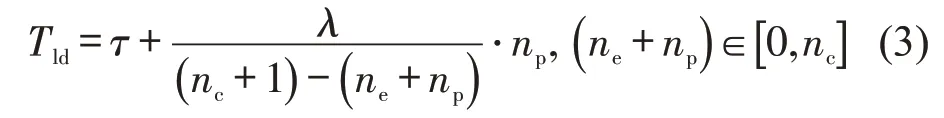
式中:τ为乘客放置行李的基本时间;λ为调整系数;ne、np分别为行李架上已有行李数量、乘客所携带行李数量;nc为行李架容量,即可放置的最大行李数。
座位干扰延误大小主要取决于让座乘客的数量。在一次让座过程中将已落座乘客起身出来和待落座乘客进入座位这两个过程时间视作相等,即

式中:μ取值代表出(进)座位的过程时间;nbs为需要让座的乘客数量。
1.2 客舱描述
在航空登机过程中,过道中行走乘客的两侧各有一条空隙道Il和Ir,可提供给乘客超越后侧身行走,当乘客不发生超越行为时会在过道中间的走道行走。乘客在登机过程中的位置状态是且仅是以下3 种之一:走道中、空隙中、座位中。因此,乘客登机过程可以通过元胞自动机模型模拟。
不失一般性,如图1所示,一架150座的标准民用航空单通道窄体飞机(A320)的经济舱区域被划分为座位区、走道区和超越区。其中超越区(空隙道)在走道区(过道)的两侧,宽度均为过道的1/2。通道两侧各是3 排座位,分为靠窗、中间、靠过道。因此,在构建元胞自动机模型中共有25×9个元胞,座位元胞的尺寸为60 cm×60 cm,过道元胞的尺寸为60 cm×45 cm,空隙道元胞的尺寸为60 cm×22.5 cm。每个区域的元胞状态分为空闲和被占用两种,赋予每个乘客其对应的i,i∈{1,2,…,nt} ,其中,nt为乘客总人数。乘客i在客舱的登机过程中,不同位置的元胞状态与乘客i的对应关系为:同时刻下乘客i只会占用走道中某位置A(p)的元胞或空隙中某位置Il(p)(Ir(p))的元胞或该乘客座位Si的元胞。
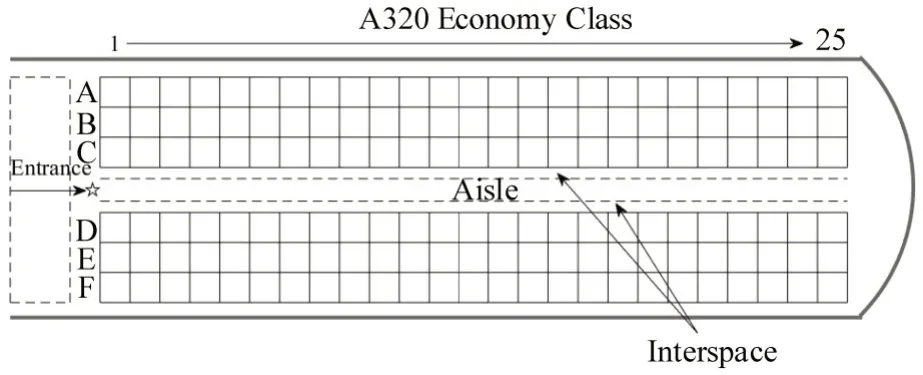
图1 空客320窄体机经济舱仿真图Fig.1 A320 narrow-body aircraft economy class simulation
1.3 乘客运动速度模型
本文在强生杰等[11]乘客跟随模型的基础上,进一步考虑行李数量的影响,提出乘客在过道中的行走速度,计算方法为

式中:v(t)、p(t)、p(t)f分别为t时刻乘客的速度、乘客的位置、乘客前方距离最近乘客的位置;np为乘客所携带行李数量。在t时刻下,当p(t)f-p(t)超过vmin时,下一时间步乘客将以1-ε·np的概率加速前进,速度大小为p(t)f-p(t)-1,ε为衰减系数;而当p(t)f-p(t)减小时,下一时间步乘客减速,直至v=0,发生行走干扰,Tmd=Tmd+1。vmin、vmax分别取1元胞每时间步和2元胞每时间步。式(5)描述了当前方无阻塞情况下,乘客i将以不低于vmin的速度行走,直至其座位所在列Si(j)停下。
1.4 乘客超越行为模型
在航空登机过程中,如果乘客在机舱过道的阻塞队列中停滞将导致其行走干扰延误增加。当行走干扰延误超过一段时间,乘客将产生超越的倾向。这里的时间段长度被定义为临界超越时间。调查结果表明,乘客是否产生超越行为受3个因素影响:携带行李数量,阻塞位置到座位所在列的距离,阻塞位置到座位所在列的过道中阻塞人数的占比。当乘客携带2件行李时,超越其他乘客与携带1 件行李相比较为困难,因此携带2 件行李的乘客更倾向于在队列中继续等待,其临界超越时间也就高于携带1件行李的乘客;在行李数量相同的情况下,乘客所在位置与座位所在列的距离越远,到座位所在列的过道中阻塞人数的占比越高,临界超越时间越小,这是因为乘客i希望更快和更早地到达座位所在列Si(j)。因此,临界超越时间为


式中:Tot,cv、Tot,m、Tot,p分别为乘客的临界超越时间、基本超越时间、可变超越时间;分别为乘客携带行李数量、乘客所在位置到座位所在列的距离、阻塞位置到座位所在列的过道中阻塞人数的占比;α、β、γ均为调节系数。其中,基本超越时间Tot,m是一个固定值,其决定临界超越时间的最小取值,而可变超越时间Tot,p是临界超越时间的主要组成部分,由式(7)确定。
接下来介绍乘客的超越行为规则。假设在走道中行走的乘客位于A(p),其将遵循如下超越规则。
Step 1Tmd=0。
Step 2 判断前方位置A(p+vmin)的状态是否为被占用。若是,转入Step 3;若否,乘客遵循乘客运动速度模型继续在走道中行走。
Step 3Tmd=Tmd+1;
Step 4 判断是否Tmd>Tot,cv。若是,产生超越倾向,转入Step 5;若否,转入Step 2,
Step 5 判断空隙道中Is(p+vmin)是否被占用,其中s∈{left,right} 。若是,Tmd=Tmd+1 ,重复Steps 5;若否,乘客状态从A(p)移入Is(p+vmin),进入超越状态。定义当乘客i的座位Si位于过道左侧,乘客选择Il(p+vmin);当乘客i的座位Si位于过道右侧,乘客选择Ir(p+vmin)。
当乘客进入超越状态后,将在空隙道中行走,这个行走过程类似在过道中行走,但因为空隙道空间受限,乘客将以稳定的速度vmin前进。同样,当乘客位于Is(p),若Is(p+vmin)的状态为被占用,Tmd=Tmd+1。
通常来说,乘客不会在空隙道内一直走到其座位所在列Si(j)。在空隙道中行走是乘客在阻塞状态下产生超越行为的结果,乘客依然倾向在过道中行走,故当乘客超越阻塞队列,重新回到过道行走。同时,假定乘客不能在空隙道放置行李。
Step 6 位于Is(p)的乘客,判断斜前方过道是否出现空闲段Afree。
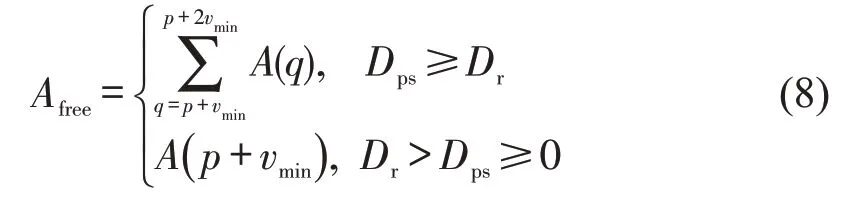
式中:Dr为决定不同空闲段距离的临界空闲距离,根据调查结果,Dr=2。
若否,乘客下一步行为也取决于Dps。当Dps≥Dr,乘客尚可继续在空隙道中前进,同样,若Is(p+vmin)空闲,则前进;若Is(p+vmin)被占用,则Tmd=Tmd+1。而当Dr>Dps≥0 ,即乘客即将到达Si(j),乘客将不得不回到过道,Tmd=Tmd+1,行走延误累加直到Afree出现。
考虑超越行为后,乘客进入客舱后的模拟流程如图2所示。当基本超越时间Tot,m的取值为无穷大时,临界超越时间Tot,cv也将为无穷大,这时阻塞队列中的乘客不会发生超越行为,乘客超越行为模型退化为传统的登机模型。
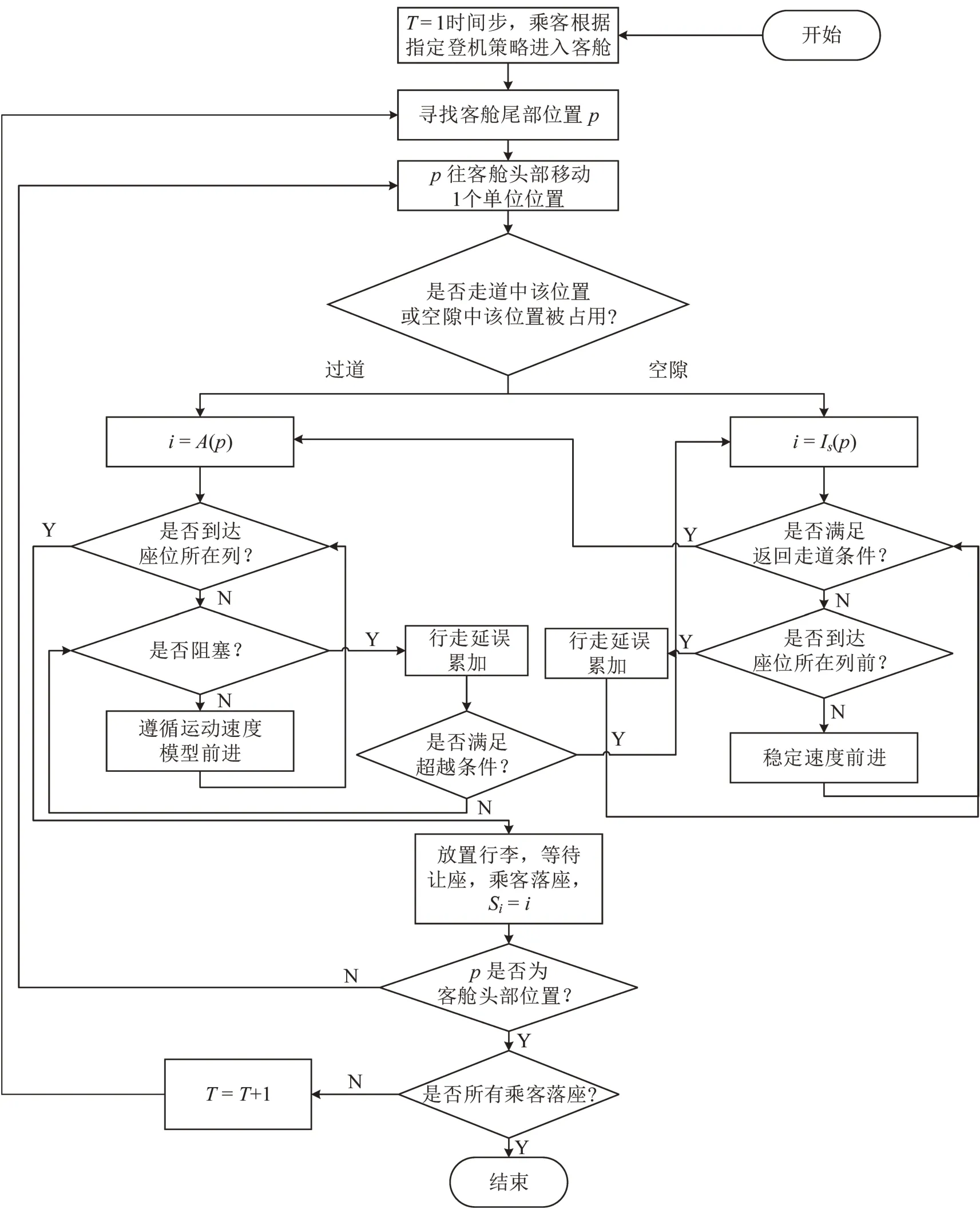
图2 乘客进入客舱后模拟流程图Fig.2 Simulation flow chart after passengers enter the cabin
2 登机策略效率分析
2.1 参数设置
仿真参数设计如下:参照文献[9-10],行李干扰延误模型中,调整系数λ=10,根据乘客携带行李数量的最大限制为2 件,行李架容量nc=6,乘客放置行李基本时间τ取1.5 个模拟时间步;座位干扰延误模型中,单个乘客进出座位时间μ取2个模拟时间步。本文中1模拟时间步等于2.4 s;干扰延误模型的计算值往正无穷方向取最小整数;乘客所携带的行李类型均为背包、手提袋。
基于客舱中客座数量特点,本文分析8种登机策略,分别为Random(随机,后文简称Rand)、BF3(分3种次序从后到前)、BF4(分4种次序从后到前)、BF5(分5 种次序从后到前)、WA3(从靠窗到过道)、RP4(倒金字塔)、Row(行策略)、Steffen 策略。为消除随机因素的影响,每种策略仿真100 次,登机时间值取记录结果的算术平均值。
2.2 超越行为对Rand策略登机效率的影响
Rand 策略因其规则限制少且易于理解被众多航空公司采用和登机乘客接受,首先仿真对比Rand策略下有超越行为(Tot,m取4个模拟时间步)和无超越行为(Tot,m取无穷大)的乘客登机过程。设置乘客放行间隔为3个模拟时间步,携带行李数量为1 件和2 件的乘客数量比例分别为60%、40%,乘客超越行为模型中调节系数α、β、γ分别取6、0.1、3,乘客运动速度模型中衰减系数ε取0.1。
首先对比有无超越行为下进入客舱通道和落座人数在登机过程中的变化情况,如图3所示。由图可见,在348 s前,有无超越行为的进入客舱人数的增加速率基本一致,而348 s后,无超越行为的进入客舱人数随时间的增加速率间歇性地减慢,有超越行为的进入客舱人数随时间以较稳定的速率增加,直到564 s后增速开始间歇性地减慢,且减慢的频率和程度都低于无超越行为的情况。最终完成所有乘客进入客舱通道,无超越行为比有超越行为多耗时100.8 s。至于落座情况,在520.8 s 前,有无超越行为的客舱中落座人数随时间的增长速率在大部分时间相近,而520.8 s 后,有超越行为的客舱中落座人数随时间接近线性增加,无超越行为的客舱中落座人数的增加速率明显减慢,且在520.8~780.0 s 和1039.2 s 之后降低明显。最终完成所有乘客落座,无超越行为比有超越行为多耗时158.4 s。

图3 超越行为对Rand策略下乘客进入客舱通道效率与落座效率的影响Fig.3 Effect of overtaking behavior on efficiency of passenger access to cabin aisle and efficiency of seating under Rand strategy
图4 进一步展示了Rand 策略下有无超越行为的仿真登机过程。图中位置在走道、空隙道、座位的椭圆分别代表处于正常行走状态、超越状态和落座状态的乘客。对比可见,同时刻下无超越行为的客舱通道中乘客行走队列的阻塞程度相较于有超越行为更严重,且随着时间推进至15 min 以后,无超越行为与有超越行为下登机进程的差距不断增大。
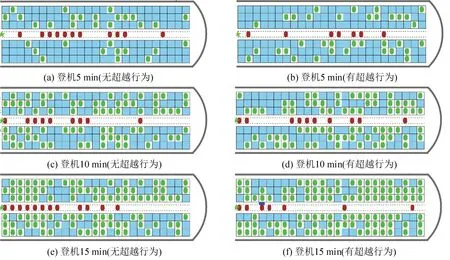
图4 乘客放行间隔ti=7.2 s下不同时刻Rand策略乘客登机情形Fig.4 Rand strategy passenger boarding at different times for passenger release interval ti is 7.2 s
考虑超越行为后,Rand 策略下的登机过程共55位乘客发生超越行为98次。如图5所示,无约束的登机次序也决定了发生超越行为的乘客座位基本平均分布在不同座位行——座位靠窗、中间和靠过道的发生超越行为的乘客分别为20,17,18 人。而座位在不同座位列的发生超越行为的乘客人数存在明显差异。由图5可见,67.27%发生超越行为的乘客座位集中在客舱后部(16~25列)。这是因为根据超越行为模型,乘客到其座位的距离会参与决定乘客是否发生超越。
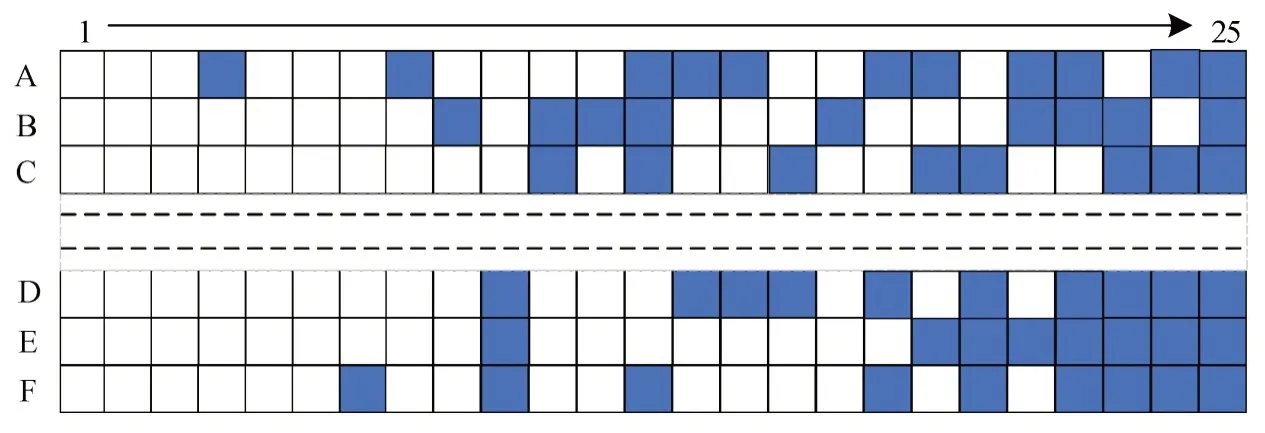
图5 Rand策略下发生超越行为的乘客所在座位(阴影部分)Fig.5 Seat of passenger who overtakes under Rand strategy(shadow)
2.3 超越行为对不同登机策略登机效率的影响
进一步地,对比其余登机策略下超越行为造成的登机效率变化情况,设置参数与2.1节和2.2节一致。以平均登机时间作为衡量登机效率的指标,对比结果如表1 所示。由表可见,在考虑超越行为后,所有登机策略的登机时间都有不同程度的缩减,且在考虑超越行为后,原本不考虑超越行为下登机时间越长策略的登机时间的缩减比例越高。考虑超越行为下WA3策略的登机效率高于RP4策略,且所有策略登机时间的差异减小,登机效率最差的Row 策略和最优的Steffen策略的登机时间差值从34.18 min减小到7.25 min。
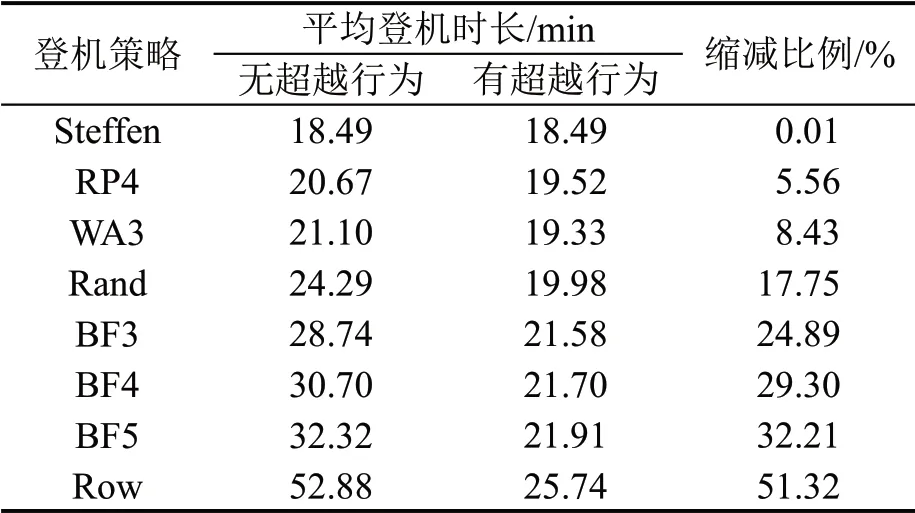
表1 有无超越行为的登机时间对比Table 1 Comparison of boarding time with and without beyond behavior
乘客人均登机时间缩减是整个登机时间缩减的重要原因。图6 展示了不同登机策略下乘客人均时间在有无超越行为下的对比情况。由图可见,考虑超越行为下的不同登机策略的人均登机时间相较于不考虑超越行为有不同比例的缩减,其中Steffen策略基本不变,变化最大的Row策略的缩减比例为42.07%,BF3、BF4、BF5 策略的缩减比例依次增大,8 种登机策略平均缩减0.77 min。且考虑超越行为后同种策略的乘客之间登机时间差异减小,所有登机策略下乘客登机时长的平均标准偏差为0.53 min,相较于不考虑超越行为缩减了0.53 min。
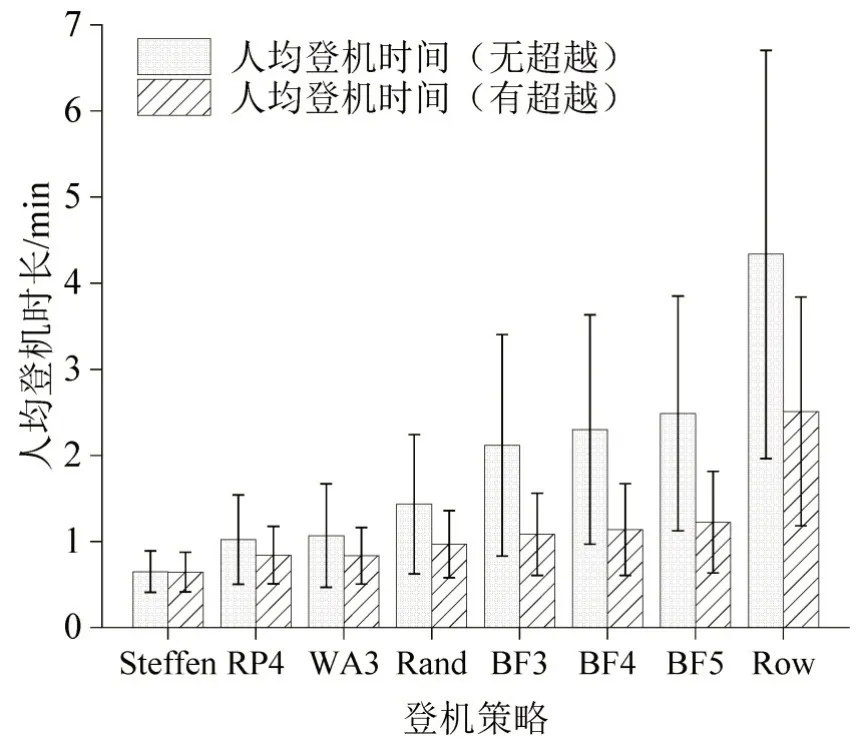
图6 超越行为对不同登机策略下人均登机时间的影响Fig.6 Effect of overtaking behavior on individual boarding time under different boarding strategies
如前文所述,3 种延误干扰时间是构成乘客登机时长的主要部分。表2 统计了有无超越行为的干扰延误时间,其中超越行为对乘客的行李干扰延误和座位干扰延误的影响极小,但对乘客行走干扰延误的影响显著。在考虑超越行为情况下,乘客行走不再受制于阻塞队列,其行走干扰延误将会在超越后保持不变或少量增加。超越行为导致的行走干扰延误大幅降低是乘客人均登机时长缩减的主要原因,而超越行为对不同策略下乘客行走干扰延误的影响程度也不同。
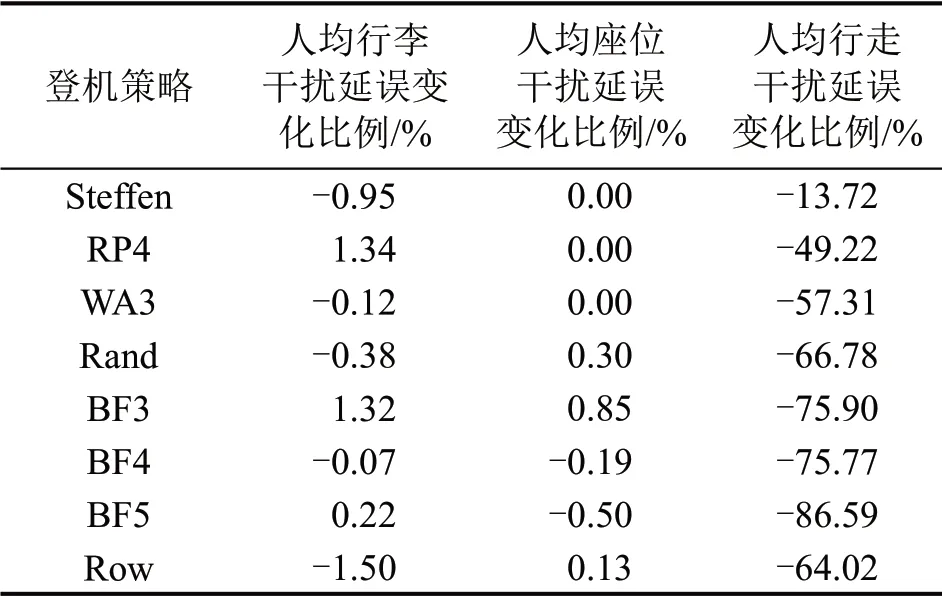
表2 考虑超越行为后乘客人均干扰延误变化比例Table 2 Percentage change in interference delay per passenger after considering overtaking behavior
结合图7(a)和图7(b)可知,Steffen 策略下的乘客保持一定间距,因此人均行走干扰延误和乘客超越的可能性都极小;WA3 策略下的人均行走干扰延误在无超越行为时大于RP4策略,而在有超越行为时却小于RP4策略。相较于RP4策略,WA3策略不区分同一座位类别(同为靠过道或中间或靠窗)乘客的登机次序,导致同一座位类别乘客登机的混乱程度高于RP4 策略,从而产生更多的超越次数,使得WA3策略的行走干扰延误缩减比例高于RP4策略;至于BF系列策略,超越次数随着划分区域数量的增加而减少,人均行走干扰延误的缩减比例却相反,超越行为对乘客行走干扰延误的减轻程度随划分区域数量的增加而增强,这是因为增加划分区域数量的同时也减小了可提供给乘客超越空隙道的空间,但一旦超越就会更顺利地到达座位所在列,因为超越位置更接近座位所在列。但这一趋势并不会一直保持,Row 策略可视作BF 系列策略的极限形式(BF25),超越行为对Row策略下人均行走干扰延误的减轻程度并不太高,乘客可占用空间极其有限,导致超越后乘客也只是在空隙中等待;值得注意的是,发生超越次数最多的Rand 策略下平均每1.4 个乘客就发生1 次超越,但对乘客行走干扰延误的影响最小。这是因为,Rand 策略下发生超越行为的乘客并未显著增多,大量的超越次数来自于发生不止一次超越的部分乘客。Rand策略下的登机过程不体现秩序性,乘客很可能反复在突然停下的乘客后方发生超越,随即又回到过道内。例如图5中座位在C行23列和C行24列的两位乘客,登机序号i间隔为3,登机时刻间隔为21.6 s,两位乘客到座位的行走过程中各自发生2 次超越行为。阻塞队列处于少量消散和集聚的交替状态,超越行为对行走干扰延误的缩减并不算显著。
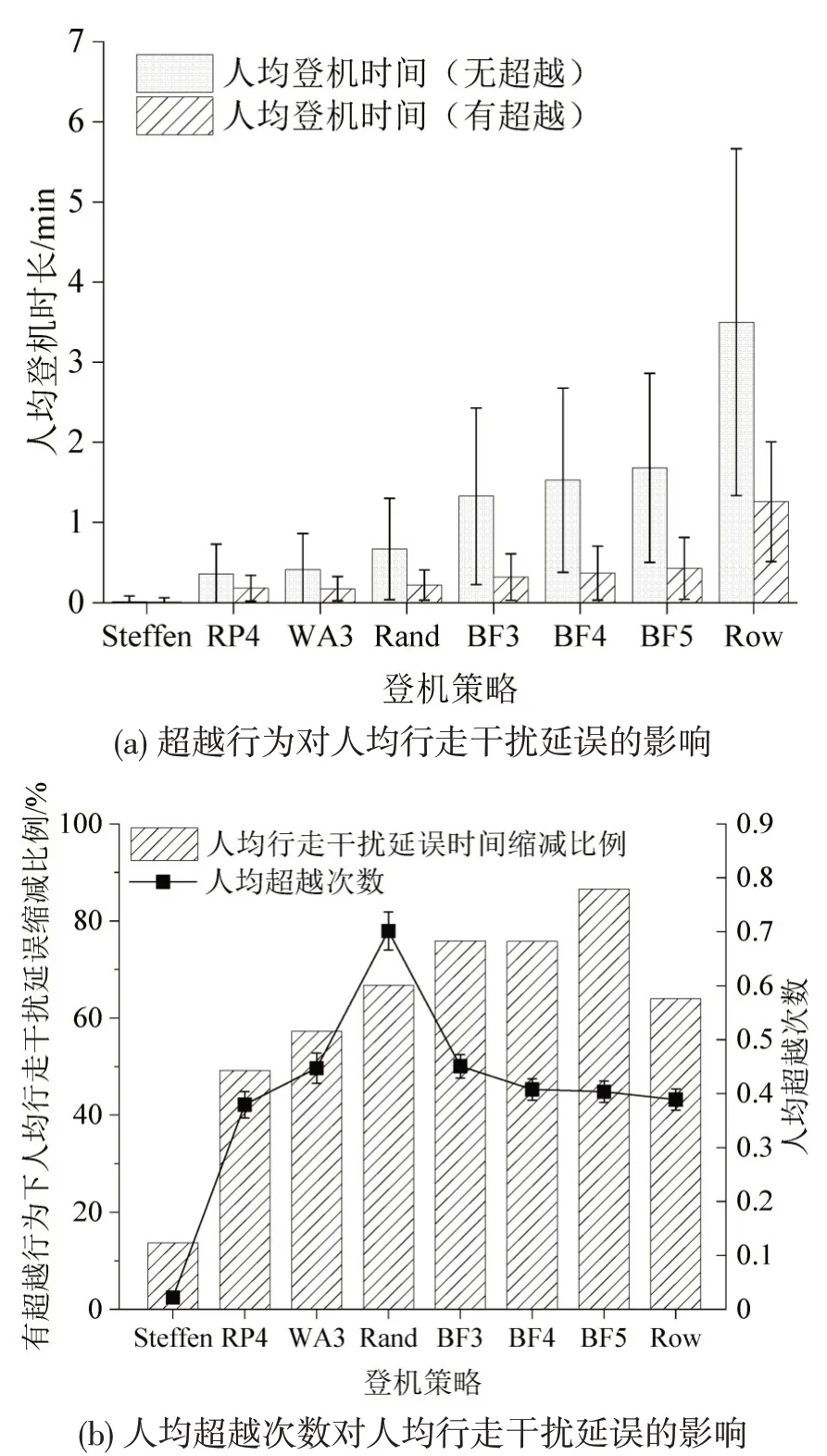
图7 超越行为对不同登机策略下行走干扰延误的影响Fig.7 Effect of overtaking behavior on walking interference delay under different boarding strategies
3 敏感性分析
3.1 不同行李数量下超越行为对登机策略效率的影响
考虑乘客携带行李数量的不同比例情况,设置携带1 件行李的乘客数量比例为r,r分别取0.0、0.2、0.4、0.6、0.8和1.0,其余参数与2.1节和2.2节保持一致,仿真无超越行为和有超越行为的乘客登机过程。通过对比图8(a)和图8(b)看出,考虑超越行为时:随着行李数量减少,所有策略的登机时间呈现3种不同变化趋势,其中,Steffen策略基本不变,Row策略以最快速度缩减,Rand策略次之;其余策略的登机时间缩减速度介于Rand和Steffen策略之间,并随行李数量的减少逐渐减慢,其中RP4 策略缩减速度高于WA3 策略,这与无超越行为恰好相反;BF 系列策略缩减的速度从BF3 到BF5 依次降低。
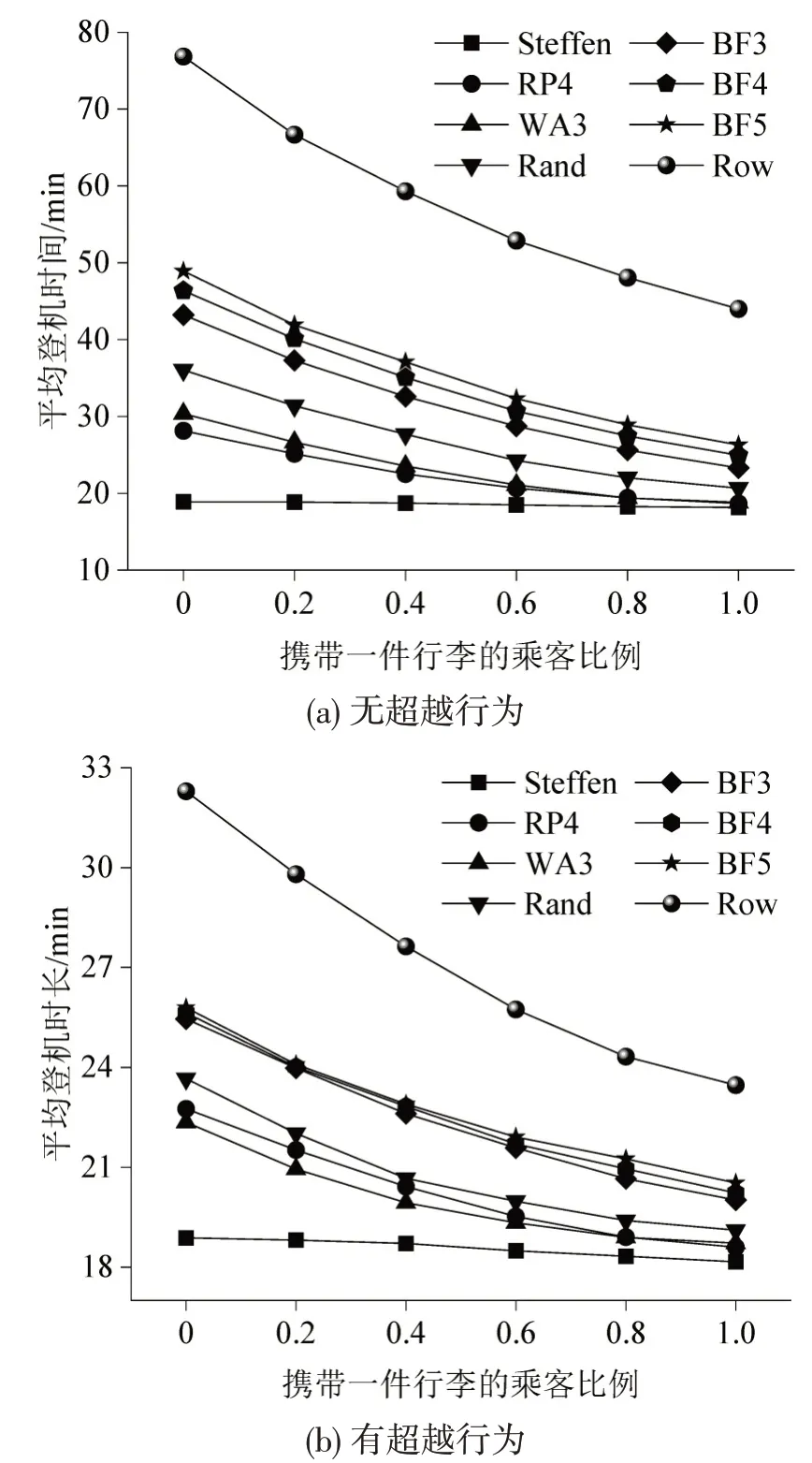
图8 不同行李数量下的登机过程平均登机时长Fig.8 Average boarding time of boarding process with different amount of luggage
进一步对比不同行李数量下有超越行为相较于无超越行为的登机时长缩减比例,研究超越行为在不同行李数量情景下的影响作用。由图9 和图10 可见:当所有乘客行李数量为1 件时,RP4 和WA3 策略下的登机过程几乎不发生超越行为;当携带2件行李的乘客比例增至40%及以上时,更多的超越行为对WA3 策略效率的影响超过RP4 策略。如图10 所示,RP4 策略和WA3 策略下的乘客行李干扰延误时间都因放置行李时间的变长而接近同样趋势增加,客舱中等候放置行李乘客的行走干扰延误时间也同样将整体增加;WA3 策略下的乘客相较于RP4策略更易发生超越,其平均每次登机的超越次数也以更快的趋势增加,这是因为RP4策略增加了区分前后座位的乘客次序。如图11所示,相较于WA3 策略,RP4 策略下的乘客在客舱中部的平均超越次数明显低于WA3 策略,相较于客舱首尾位置也大幅减少。更少的超越行为次数归因于座位在靠过道和中间两排区域的乘客因为区分登机次序均不易形成过长的阻塞队列。随着平均行李干扰延误的增大,超越行为对WA3 策略下的乘客登机进程影响更大;随着乘客行李数量的增加,超越行为对Rand、BF3、BF4、BF5策略下效率的影响以相近的速度增大,但对Row策略下效率的影响以极小的速度增大——不同行李数量下超越行为对Row 策略效率的影响保持在一个高且稳定的水平。建议航空公司在乘客行李数量少时优先选用RP4 策略,而乘客行李数量多时优先选用WA3策略。
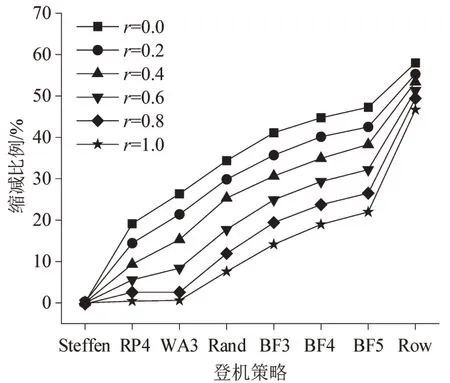
图9 不同行李数量下有超越行为相较于无超越行为的平均登机时长缩减比例Fig.9 Average reduction in boarding time with overtaking compared to without overtaking for different amount of luggage
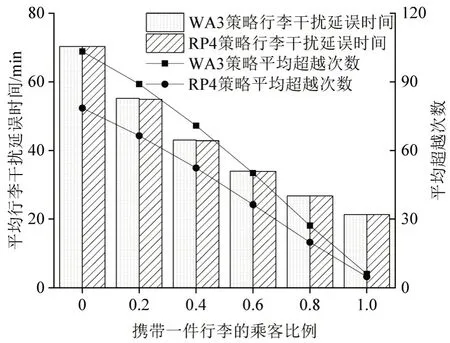
图10 不同行李数量下WA3和RP4策略下乘客行李干扰延误时间和平均超越次数对比Fig.10 Comparison of passenger luggage interference delay time and average number of overtaking under WA3 and RP4 strategies with different luggage quantities
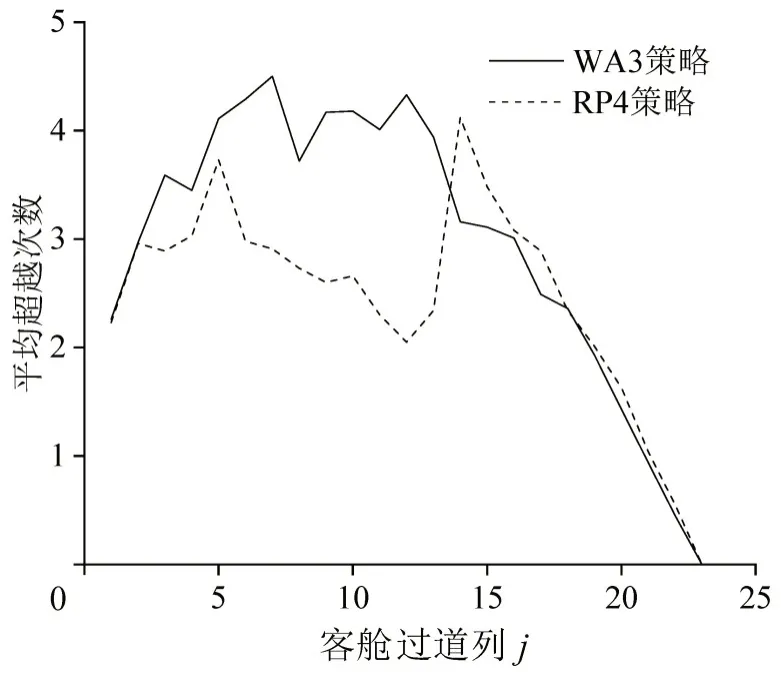
图11 WA3策略、RP4策略不同客舱过道位置平均超越次数对比Fig.11 Comparison of average number of overtaking in different cabin aisle positions of WA3 strategy and RP4 strategy
3.2 不同放行间隔下超越行为对登机策略效率的影响
设置乘客放行间隔分别为4.8,7.2,9.6,12.0,14.4 s,其余参数与2.1节和2.2节保持一致,模拟考虑超越行为的登机过程,无超越行为和有超越行为不同登机策略的登机时间分别如图12(a)和图12(b)所示。值得注意的是,无超越行为时,随着放行间隔的增大(减小),Row 策略的登机时间基本不变;其余策略登机时间的变化速度依次降低(提高),这一趋势在放行间隔介于9.6 s 和12.0 s 时体现明显。有超越行为时:Row策略的登机时间不存在保持不变,这是因为允许超越的情形中,所有策略下登机乘客的行走干扰延误已尽可能降至最低,当乘客放行间隔增大时,被超越行为缓解的阻塞情况很少,登机时长只会因乘客进入客舱通道的速率下降而增长。此外,当放行间隔超过7.2 s 以后,RP4 策略的登机效率超过WA3策略。
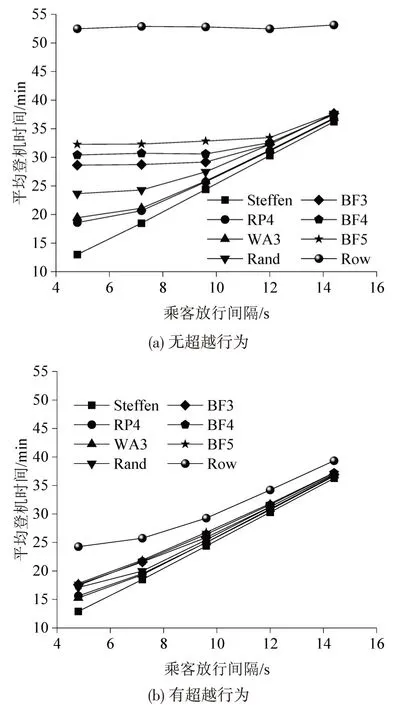
图12 不同放行间隔下登机过程平均登机时长Fig.12 Average boarding time of boarding process at different release intervals
图13展现了不同放行间隔下有超越行为相较于无超越行为的平均登机时长缩减比例。当放行间隔超过7.2 s后,超越行为对RP4策略效率的影响大于WA3 策略,原因同样是WA3 策略仅按行区分登机次序的规则,可能导致乘客保持的前后间距更大,因此在放行间隔很大时,超越行为的影响作用小于RP4 策略。建议航空公司在乘客放行间隔小时优先选用WA3 策略,而乘客放行间隔大时优先选用RP4 策略。随着放行间隔增大,超越行为对Steffen、RP4、WA3、Rand、BF3、BF4、BF5 策略效率影响的下降趋势依次增大,而对Row策略效率的影响趋势整体接近于Rand策略。当放行间隔从4.8 s增至14.4 s,超越行为对BF5 策略效率的影响水平下降最多,此时有无超越行为所有策略的效率都基本无变化。实际上,划分登机次序越多的登机策略形成的阻塞队列越短,且随放行间隔的增大,阻塞队列的消散速度越快,超越行为对登机效率的影响减小得越快。
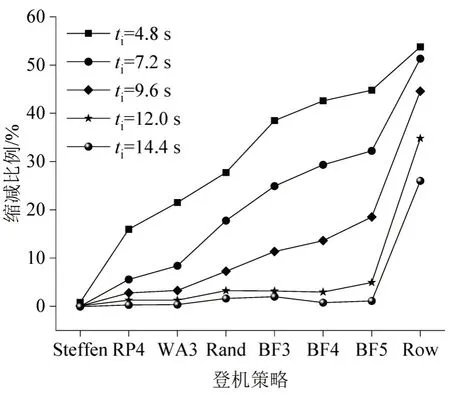
图13 不同放行间隔下有超越行为相较于无超越行为的平均登机时长缩减比例Fig.13 Average reduction in boarding time with overtaking compared to without overtaking at different release intervals
3.3 不同客座率下超越行为对登机策略效率的影响
在实际航空登机中常常出现客舱并非满座的情况,故保持其余参数与2.1 节和2.2 节一致,设置不同客座率a(50%,60%,70%,80%,90%),进一步模拟不同客座率下无超越行为和有超越行为的登机过程,无超越行为和有超越行为不同登机策略的登机时间分别如图14(a)和图14(b)所示。由图可见,当客座率小于100%时,考虑超越行为后显著变化是:BF系列策略中效率最高的不再是BF3策略,而是BF4 策略;甚至在客座率为70%时,BF4 是所有策略中效率最高的。伴随客座率上升(下降),Steffen、RP4、WA3 等策略效率受超越行为影响的变化规律不再是单调提高或降低。客座率介于80%~100%是航空公司最常面临的情况,如图15所示,在这个区间内,超越行为对WA3和Rand策略的影响遵循随客座率上升而增大的规律,但对BF 系列和Row策略的影响规律却不同。
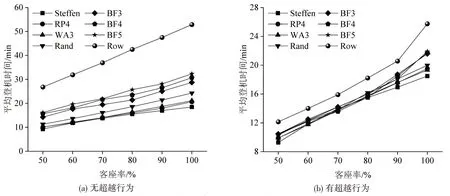
图14 不同客座率下登机过程平均登机时长Fig.14 Average boarding time of boarding process at different passenger load factor

图15 不同客座率下有超越行为相较于无超越行为的平均登机时长缩减比例Fig.15 Average reduction in boarding time with overtaking compared to without overtaking at different occupancy rates
值得注意的是,不同于前文两种登机情景,不同客座率下不同登机策略有超越行为相较于无超越行为的平均登机时长缩减比例的排名也并非一致。体现在70%客座率下BF4 策略的缩减比例高于BF3策略和BF5策略。关注这一变化,首先对满座情景下BF4 策略的登机进程进行研究。由图16发现,BF4策略下登机过程超越行为的发生位置主要集中在前后登机次序区域的分界列过道和分界列的前一列过道,这是因为发生超越行为的乘客基本是在对应次序区域内最晚登机,根据超越行为模型,当行走干扰延误增加,这些乘客集中在区域分界处超越。例如,图16中第13列作为BF4策略第2和第3次序登机区域的分界,此位置的平均超越次数高达11次。当超越行为增多导致分界列空隙道被占据后,分界列的前一列过道将充当候补超越位置。这意味着,当登机乘客的人数尽可能恰好填满每一次序区域时,未考虑超越行为的登机效率将与考虑超越行为时达到最大差距。也就是说,尽可能减少下一次序区域登机乘客的人数,将增大超越行为对登机过程的影响。在70%客座率(105 人)下,BF4 策略的1~3 登机次序区域(108 人)很好地贴合上述情形。类似地,60%和80%客座率下,超越行为对BF5 策略登机时间的缩减比例相较于其余客座率平均增加2.2%,同样印证了这一分析。
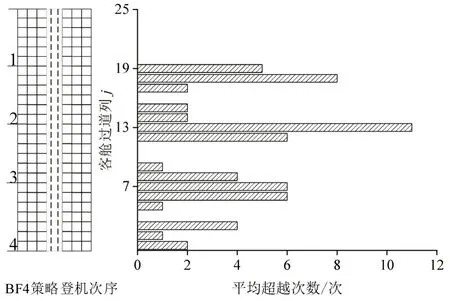
图16 BF4策略下乘客超越行为位置分布Fig.16 Location distribution of passenger overtaking behavior under BF4 strategy
3.4 不同Tot,m 和ε 取值对登机策略效率的影响
乘客超越行为受超越行为模型中超越基本时间Tot,m取值的影响,乘客运动速度受运动速度模型中衰减系数ε取值的影响。乘客不同运动速度会导致不同的行走干扰延误,从而影响乘客的超越行为。因此本节保持其余参数不变,设置超越基本时间Tot,m和衰减系数ε的不同取值,模拟Rand 策略下有超越行为的登机过程,结果如图17 所示。值得注意的是:当Tot,m未超过38.4 s时,最短平均登机时间对应的ε都不是0.1——在Tot,m等于9.6,19.2,28.8 s 时最佳ε分别为0.20、0.15、0.20;当Tot,m超过38.4 s 时,平均登机时间随ε的增大而增长。这是因为当乘客的临界超越时间很短时,降低乘客的运动速度,可能减轻客舱通道中乘客的集中分布程度,降低了阻塞程度加剧的可能性;当乘客的临界超越时间很长时,发生超越行为的乘客很少,运动速度高的乘客会更早地加入阻塞队列,从而加剧阻塞程度,且因为很多乘客倾向等待最终增加了总登机时间。

图17 衰减系数ε、超越基本时间Tot,m 对有超越行为的Random策略平均登机时长的影响Fig.17 Effect of decay coefficient ε,overtaking basic time Tot,m on average boarding time of Rand strategy with overtaking behavior
4 结论
本文考虑航空登机过程中客舱内乘客的超越行为,通过元胞自动机模拟了从乘客进入客舱通道到完成落座的登机过程,通过对不同登机策略下超越行为的发生次数、发生位置以及发生乘客对应的座位分布进行研究,分析超越行为对不同登机策略效率的影响机理。主要结论如下:考虑超越行为后,登机策略的登机时间缩减比例由高到低依次为Row、BF5、BF4、BF3、Rand、WA3、RP4 和Steffen。乘客行走干扰延误降低是登机时间缩减的主要原因。登机策略下乘客行走干扰延误受超越行为的影响程度由高到低依次为Steffen、BF5、BF3、BF4、Row、RP4、WA3、Rand。本文进一步研究了考虑乘客超越行为下不同登机策略在不同行李数量、乘客放行间隔和客座率下的效率表现,重要结论如下:WA3 策略在乘客携带2 件行李数量的比例超过40%或乘客放行间隔低于7.2 s 情景下的登机效率优于RP4 策略。BF4 策略在客座率70%左右的情景下效率为最优,其余客座率情景下,BF系列策略的划分区域恰好容纳登机乘客人数时,超越行为对登机效率的影响作用最大。

