社会偏好视野下旅游出行服务链定价博弈模型

李婉莹，关宏志，韩艳，曹杨柳

（北京工业大学，交通工程北京市重点实验室，北京 100124）

0 引言

随着信息和通信技术（Information and Communication Technology,ICT）的广泛应用，基于应用程序的出行服务，例如，Uber，Car2Go，Didi，Mobike 在众多城市和地区不断出现，促进了共享出行方式的发展。技术的进步也带来了新的商业模式，例如，在提供商和消费者之间加入具有交互作用的中间商，在这样的背景下，以“使用而非拥有交通工具”为核心理念的出行即服务（MaaS）迅速兴起。MaaS 即基于智能终端的“一站式”出行服务，通过提供多种出行方式和出行相关服务满足出行者需求。我国拥有全球最大的出行市场，以共享出行服务为例，2017年，全国互联网租赁自行车运营企业超50家；2018年，全国注册的分时租赁共享汽车企业已超500 家；2019年，北京市交通委与高德地图共同启动了北京交通绿色出行一体化服务平台（北京MaaS 平台）。MaaS 作为一种门到门间不同交通模式高度整合的出行服务，在我国具有广泛的市场前景。在未来城市社会中整个交通方式和出行服务充足供应的假设下，考虑到出行者旅游出行行为的特点，可以在MaaS 的个性化服务中专门设置旅游服务与出行服务组合的旅游出行服务套餐。在MaaS环境下，出行者可以选择直接在MaaS平台上订阅旅游出行服务套餐（包括：旅游服务和出行服务），而无需在多个平台上多次购买景区门票和交通票。可见，旅游出行服务链中的两个决策者-服务提供商与MaaS 平台之间存在既竞争又合作的关系。决策者之间的合作有利于双方自身和整体服务链的可持续发展，决策者之间的利益冲突将导致整个供应链的效率损失。因此，协调决策者之间的利益冲突和实现旅游出行服务链优化尤为重要，有必要对服务链中的双方合作定价问题进行理论研究，并探讨各主体的决策行为及其对双方自身和服务链整体最优决策的影响。

目前，已有文献针对MaaS 存在的复杂性和不确定性进行了一系列探索，主要分为非实证研究（理论研究）和实证研究两类，包括：MaaS 概念及系统框架设计、应用方法、用户偏好和支付意愿及不同政策下的应用效果等，但均未涉及不同场景下MaaS服务链中各决策者的定价博弈问题。随着博弈论在交通中的应用日益广泛，考虑主导权的Stackelberg博弈模型为MaaS服务链的研究提供了思路。马继辉等[1]基于不同的合作水平使用纳什议价效用函数模拟议价过程，建立航空主导的和具有议价行为的收益共享Stackelberg博弈模型，采用逆向归纳法求解博弈模型。段华薇等[2]基于两种随机市场需求函数分别构建了高铁快递和传统快递主导下的Stackelberg博弈模型，分别得到高铁快递的最优协议运价策略和传统快递的最优协议运量及市场运价策略。周健等[3]建立了以纯网络零售商为主方和以双渠道零售商为主方的Stackelberg 主从对策博弈模型，比较了不同定价时间策略下电子渠道的市场规模和双渠道零售商电子渠道的市场规模占整个电子渠道市场规模的比例对供应链成员最优定价的影响。

传统讨论决策者之间互动博弈的研究建立在微观经济学理论“理性即自利”的假设之上，然而，基于自利的决策无法解释诸多经济学实验（例如，最后通牒实验、独裁者实验及信任博弈）中的系统性偏离[4]。随着有限理性假说的提出、行为经济学的崛起和实验方法的广泛运用，基于社会偏好理论的决策研究受到了学界的普遍关注。根据CARPENTER[5]的定义，如果（个体）除了关注自身的支付外，还同时关注其他相关参照当事人的支付以及导致这些偏好的意图，那么该个体就具有社会偏好。他们发现个体的社会偏好可以归结为不平等厌恶偏好、利他偏好、互惠偏好和认同偏好这4类[6]，同时，一定程度偏离自利的收益追求会带来竞争优势[7]。其中，不平等厌恶偏好，即个体关心相对损益并存在损失厌恶，例如，FEHR等[8]提出的线性模型（FS 模型）和BOLTON 等[9]提出的非线性ERC（Equity, Reciprocity, and Competition）模型（BO 模型）所刻画的那样，个体的效用取决于自身的收益以及自身收益与他人收益之间的差异。利他偏好指社会中的个体会主动地、自发地和不计代价地帮助他人且不求回报，是一种纯粹的社会偏好[10]。互惠偏好指社会中的个体会在意图上展示出友善并相互实施友善行为，这种意图互惠有时候也可以理解成公平偏好[11]。认同作为社会偏好，体现了社会中个体与群体在信念上的高度一致性[12]。

近年来，考虑决策者社会偏好的供应链决策研究开始受到关注，学者们多基于两级供应链构建主从博弈模型，且大部分文献均假设仅处于跟随地位的决策者具有不平等厌恶偏好和仅处于主导地位的决策者具有利他偏好。冯中伟等[13]以Nash 谈判解作为制造商的损失厌恶参考点，探究制造商的损失厌恶偏好对自主减排低碳供应链决策的影响。张廷龙等[14]引入收益共享契约，缓解利润分配不公平引起的渠道冲突，通过Stackelberg博弈理论研究了旅游供应链中各成员的决策策略。GE[15]引入决策主体的利他偏好建立合作竞争模型，系统讨论了集中式、分散式和合作竞争下的供应链定价、需求和收益问题。上述研究从不同侧面反映服务链决策者之间的复杂关系及博弈过程，但没有详细考虑决策者的社会偏好特征和市场的需求价格弹性特征，以及决策者定价策略对服务链收益的影响。在旅游出行服务链决策者之间的博弈互动中，最为直观的表现是价格策略选择问题，如果服务提供商在与MaaS 平台的合作过程中关注MaaS 平台的不平等厌恶偏好，或者服务提供商自身的利他偏好，决策者会如何制定各自的价格策略，该定价策略会对决策者自身和服务链整体收益产生什么样的影响？基于以上分析，本文从MaaS 背景下旅游出行服务链的发展现状出发，基于消费者效用理论，建立由占主导地位的服务提供商和处于跟随地位的MaaS 平台组成的两级旅游出行服务链Stackelberg博弈模型。考虑服务链中各决策者的社会偏好特征及其对价格制定的相互影响，探讨分散决策和合作决策模式下的均衡策略，对于实现MaaS 市场的可持续发展具有重要借鉴意义。

1 问题描述与模型构建

1.1 问题描述

MaaS 通过提供一体化交通出行和一站式服务，改善人们的公共出行体验。在MaaS 环境下，MaaS平台将服务提供商提供的各种旅游出行方式和信息重新整合成旅游出行服务套餐，并以更加优惠的价格打包提供给出行者，使出行者获得更好的体验，从而更好地满足旅游出行的需求。MaaS+旅游的应用具有一系列市场优势：①对于出行者，使用旅游出行服务可以享有出行费用折扣、个性化定制旅游出行服务、灵活安排出行日程和预算控制等；②对于服务提供商，旅游出行服务的设置可以提高交通出行资源和旅游资源的利用率，增加交通运输部门和旅游景区收益；③对于MaaS 平台，可以起到提高整体收益，推出新的（旅游出行）产品或阻止竞争对手进入市场的作用；④对于整个旅游交通系统，旅游出行服务套餐的模式可以更好地匹配供需，提高多式联运出行的效率。

服务链是由不同服务供给者通过签署契约或协议相互合作而形成的一种链式结构[16]，目的是组合服务，使得用户获得比分散服务更超值的享受。旅游出行服务链包含资源端、平台端及用户端，服务提供商与MaaS平台构成了典型的两级旅游出行服务供应链，如图1所示。

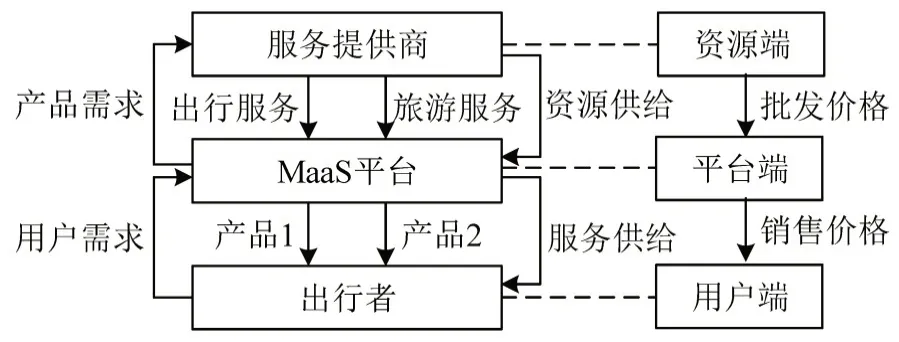
图1 旅游出行服务链Fig.1 Travel service chain

①在资源端，旅游出行服务提供商包含交通出行服务提供商和旅游服务提供商两类，共同为MaaS 平台提供交通出行服务和旅游服务。其中，交通出行服务包括传统出行服务（例如，公共汽车、有轨电车、地铁及出租车）和共享出行方式（例如，汽车共享、自行车共享及拼车），旅游服务主要为旅游信息、景区预约及门票支付等。② 在平台端，MaaS平台充分利用城市交通运输网络及大数据算法联通平台前端和后端资源，链接出行者的出行行为，实现精准用户管理，确保低成本和高效率运营。MaaS平台根据出行者的消费偏好和服务提供商供给的资源，组合并设计旅游出行服务产品向出行者销售，并为出行者提供包括行前智慧决策，行中全程引导及行后绿色激励等全流程和一站式“门到门”的出行智能诱导以及旅游出行全过程规划服务。根据出行方式的种类和使用期限，套餐类型可以分为单方式旅游出行服务套餐和多方式旅游出行服务套餐，以及包日套餐和包月套餐，如图2 所示。③在用户端，出行者关注旅游出行服务的便利性、经济性及灵活性，并关注平台端的服务效率。在订阅旅游出行服务套餐后，出行者可以使用套餐内的交通出行服务，并享有旅游信息查询、景区预约和门票折扣等服务。

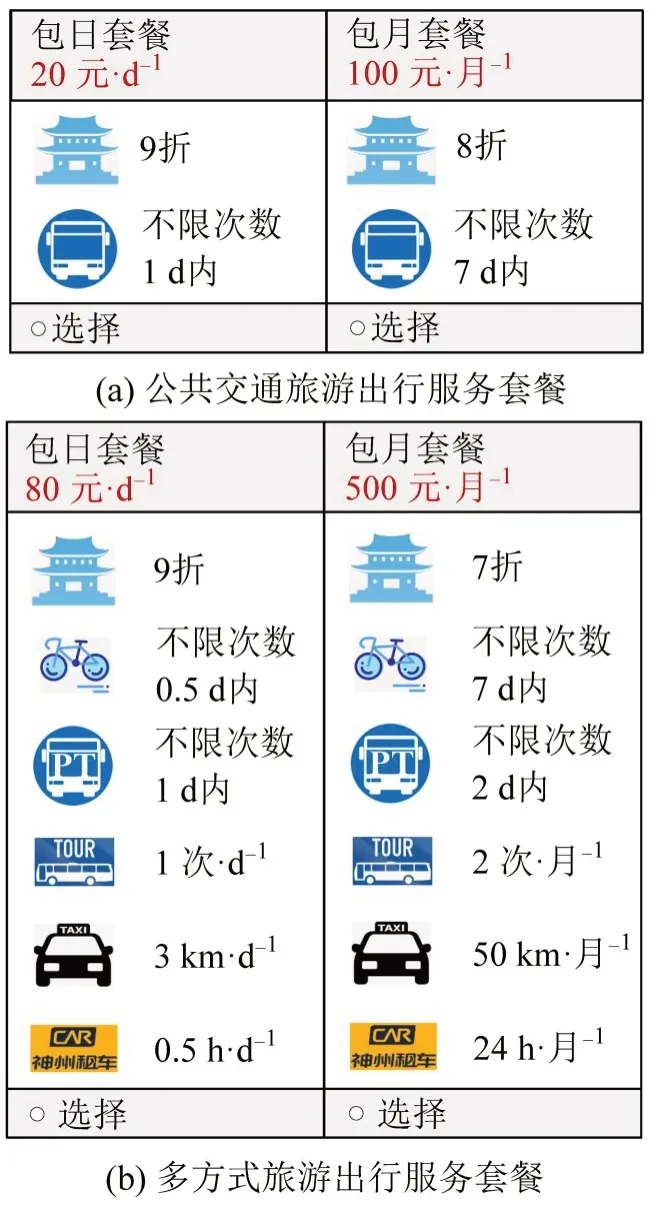
图2 旅游出行服务套餐示例Fig.2 Examples of travel-service bundles

旅游出行服务链中，决策者之间存在典型的价格互动，例如，服务提供商在通过MaaS平台销售时的批发定价，以及MaaS 平台向出行者销售旅游出行服务套餐时的定价。MaaS定价关系到服务提供商、MaaS平台和出行者三方决策者的决策行为，受决策者社会偏好的影响。处于主导地位具有利他偏好的决策者，或处于跟随地位具有不平等厌恶偏好的决策者，所采取的不公平厌恶或利他行为有利于弥合服务链中各成员之间的获益差距，促进服务链中各成员协作并提升整体绩效。因此，本文建立旅游出行服务链Stackelberg 主从博弈模型，其中，旅游出行服务提供商是服务链主导者，MaaS 平台是跟随者，服务提供商通过MaaS 平台销售旅游出行服务。引入服务提供商的利他偏好因素和MaaS平台的不平等厌恶偏好因素，研究不同决策者的社会偏好特征对旅游出行服务链的定价及服务链整体收益的影响。

1.2 模型构建

1.2.1 基本假设

本文仅考虑旅游出行服务提供商与MaaS平台之间的纵向合作关系。服务提供商和MaaS平台的博弈决策点是两种旅游出行服务产品的定价，包括批发价格和销售价格。在不失一般性的基础上，为了必要的数学简化，根据本文研究背景和目标做出以下假设。

假设1 旅游出行服务链中的决策主导者是服务提供商，决策跟随者是MaaS平台。

假设2 一般情况下，服务提供商通过MaaS 平台销售旅游出行服务产品给出行者，即不考虑服务提供商通过自身销售渠道向出行者销售旅游出行服务的情况。

假设3 服务链中决策者双方的博弈属于完全信息博弈，且该博弈存在行动的先后顺序，属于动态博弈。

1.2.2 变量定义

基于以上考虑，本文模型中涉及的符号及说明如表1所示。其中，Δe=e2-e1，Δc=c2-c1，为了保证两种旅游出行服务产品的需求量大于0，假设Δe ＞Δc。

表1 变量定义Table 1 Variable definitions

1.2.3 效用函数

根据DUMRONGSIRI 等[17]提出的效用函数模型，出行者的效用函数是关于旅游出行服务产品销售价格si和旅游出行过程中实际体验ei的函数，且不同出行者对同一种旅游出行服务产品偏好存在差异[18]。因此，第i种旅游出行服务套餐的效用函数为

式中：v为旅游出行服务产品的基本效用，对于不同服务套餐和出行者是同质的。

θ为出行者对旅游出行服务产品的偏好，服从均匀分布的随机变量，θ∈[0 ,1] 。定义θ*=可推出：

定理1 已知旅游出行服务套餐的销售价格s1和s2，出行者购买套餐的实际体验e1和e2，则存在

（1）当θ ＜θ*时，u1＞u2；否则，u1≤u2。

1.2.4 需求函数

旅游出行服务套餐2的需求函数为

1.2.5 利润函数

服务提供商的收益函数为

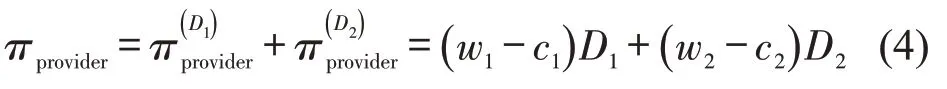
MaaS平台的收益函数为

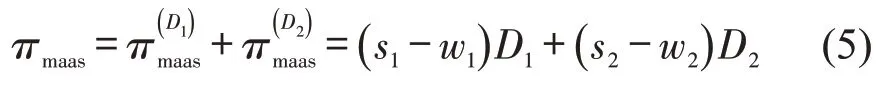
服务链整体收益函数为

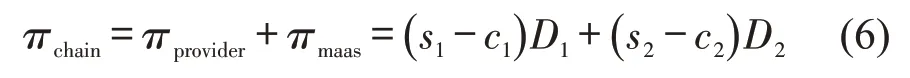
1.3 服务链基本决策模式

旅游出行服务链基本决策模式分为分散决策模式和合作决策模式两种类型，服务提供商和MaaS平台会根据不同的利益目标决定批发价格和销售价格，这是主要的博弈决策变量。博弈过程采用两阶段的完全信息动态Stackelberg博弈进行。

多种色釉于一坯胎中也是在近现代才流行起来，多种色釉的窑变比单色釉可说难，也可说易。难是难在对釉料料性的掌握，那种色釉流动，那种不流动，色釉与色釉之间能否结合，产生的效果如何，几种色釉结合当怎样的比例才能烧制出最佳效果等等，这就是难。说它容易，也只能说出现二次创作以后陶瓷艺术家才敢如此认为。颜色釉基础上的二次创作是根据艺术家对色釉窑变效果来巧妙装饰的，主观性较强，但选取的画面需要和色釉窑变气氛相吻合，才能达到异曲同工之妙。

1.3.1 分散决策模式

分散决策模式指服务链成员独立决策以最大化自身利润，占主导地位的服务提供商先确定批发价格w1和w2，然后，MaaS 平台确定销售价格s1和s2，无论是服务提供商还是MaaS 平台都将最大化自身利润。因此，服务提供商和MaaS 平台处于Stackelberg博弈中。相关变量以“De”为上标，采用逆向求解法确定Stackelberg 均衡解，计算结果如表2所示。

供应链决策者双方的利润博弈函数为

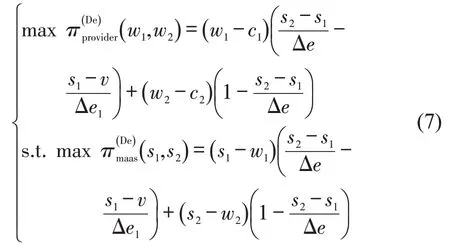
1.3.2 合作决策模式

在合作决策模式中，服务提供商和MaaS 平台是完全合作的，联合决策以旅游出行服务供应链整体利润最优为目标。相关变量以“Ce”为上标，供应链整体利润最大化问题为

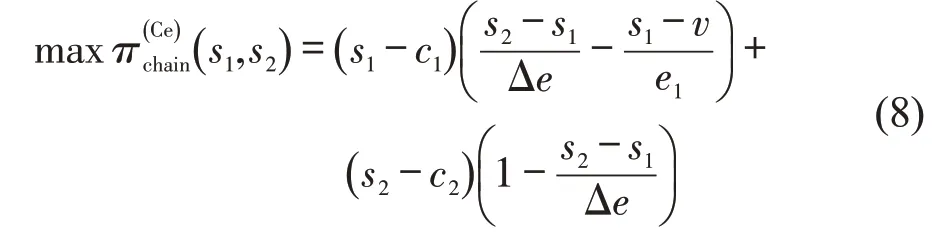
2 博弈模型的建立与求解

在社会偏好理论和服务链基本决策模式的基础上，考虑决策者社会偏好时，旅游出行服务链决策模式分为不平等厌恶决策模式、利他决策模式和社会福利综合决策模式这3 类。不平等厌恶决策模式下，服务链中（处于跟随地位的）决策者更关注博弈过程中收益在各参与者之间分配的公平性；利他决策模式（处于主导地位的）指决策者不仅关注自身的收益，还会关注其他参与者的收益；社会福利综合决策模式考虑了决策者的不平等厌恶和利他两种偏好形式，在效用函数中将各参与者的不平等厌恶和利他动机相结合的综合决策模式。

2.1 不平等厌恶决策模式

FS 模型遵循了前景理论观点，即决策者关注相对损益并表现出损失厌恶。服务链中处于跟随地位的决策者-MaaS 平台的效用不仅取决于自身的理性策略选择，还取决于自身的不平等厌恶偏好强度。在博弈过程中，决策者所得利润偏离对方越多，这种不平等厌恶程度就越强烈。因此，假设MaaS 平台是不平等厌恶的，服务提供商是不平等中性的，基于参考点依赖描述MaaS 平台的效用函数，以对方利润作为己方利润的参考点，引入参数λ作为不平等厌恶系数，得到MaaS 平台的效用函数为

MaaS 平台是不平等厌恶的，因此，λ ＞0。λ越大，表示MaaS平台的不平等厌恶程度越强烈，其效用损失也就越大。其中，当πmaas≥πprovider时，MaaS 平台的效用随着利润差异的增加而增加；当πmaas＜πprovider时，MaaS 平台的效用随着利润差异的增加而减少；当λ=0 时，MaaS 平台是不平等中性的，Umaas=πmaas，即等价于不考虑社会偏好时的服务链分散决策模式。

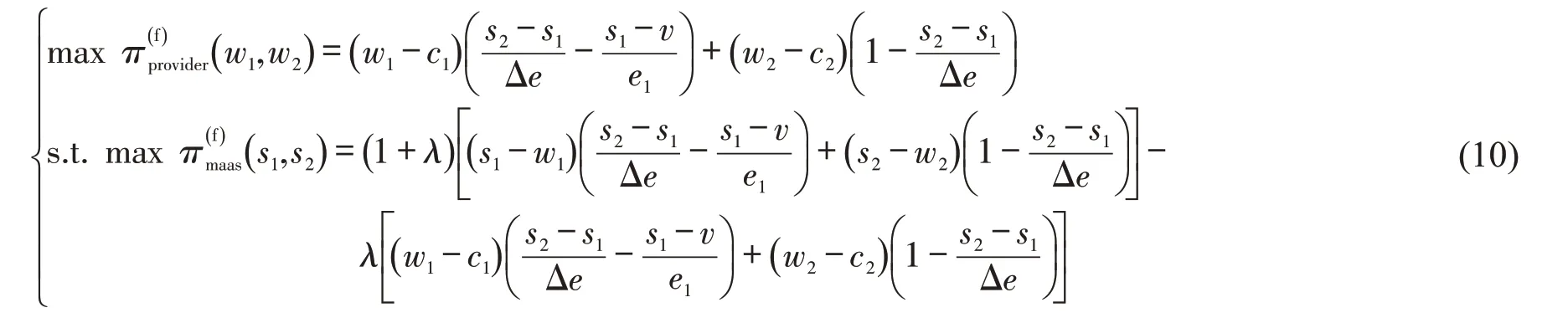
2.2 利他决策模式

为了提高服务链中的系统竞争力，服务提供商追求自己利润的同时也关心其他决策者的利润，即决策者可能既利己又利他。为此，引入服务提供商的关系参数mprovider和状态寻求偏好参数nprovider，建立考虑利他偏好的决策者效用模型，其决策目标函数为

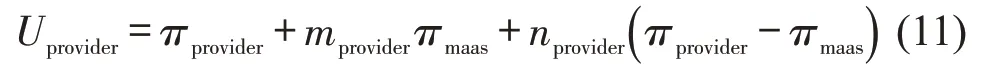
对效用函数的两边进行1+nprovider的归一化，式（11）可简化为

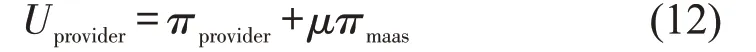
式中：μ为服务提供商的利他参数，μ=，反映了对另一方的总体关注。假设μ∈[0 ,1] ，μ=1 意味着服务提供商为完全利他型决策者；当μ=0 时，服务提供商是利他中性的，Uprovider=πprovider，即等价于不考虑社会偏好时的服务链分散决策模式。因为服务提供商更关心己方利润而非其他决策者，μ越大，表示服务提供商的利他偏好程度越强。

相关变量以“a”为上标，服务链决策者双方的利润博弈函数为

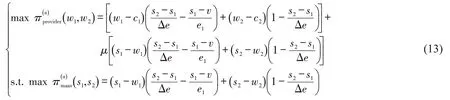
2.3 社会福利综合决策模式

在社会福利综合决策模式下，MaaS 平台以其不平等厌恶偏好效用函数作为决策目标函数，服务提供商以其利他偏好效用函数作为决策目标函数，相关变量以“fa”为上标，服务链决策者双方的效用博弈函数为

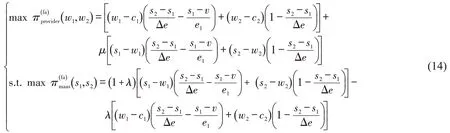
同理，采用逆向求解法可得到考虑决策者社会偏好时的均衡解。

3 不同博弈模型的比较分析

3.1 均衡解比较

通过对博弈模型、最优决策变量比较和分析，得出6个命题。其中，博弈模型包含5种，分别为不考虑决策者社会偏好时的分散决策模型和合作决策博弈模型，考虑决策者不平等厌恶偏好时的分散决策博弈模型，考虑利他偏好时的分散决策博弈模型以及考虑决策者社会福利综合偏好时的分散决策博弈模型。最优决策变量包括：旅游出行服务套餐的批发价格、销售价格、服务链中决策者收益和整体收益这3类。基本博弈模型的均衡解如表2所示。博弈模型的均衡解如表3所示。

表2 基本博弈模型均衡解Table 2 Equilibrium solution of basic game models

表3 博弈模型均衡解Table 3 Equilibrium solution of three game models

命题1表明，旅游出行服务套餐的最优销售价格在不考虑社会偏好时的合作决策模式下最大，在分散决策模式下最小（与仅考虑MaaS 平台不平等厌恶偏好下的销售价格相等），而考虑服务提供商的利他偏好下的销售价格介于两者之间。

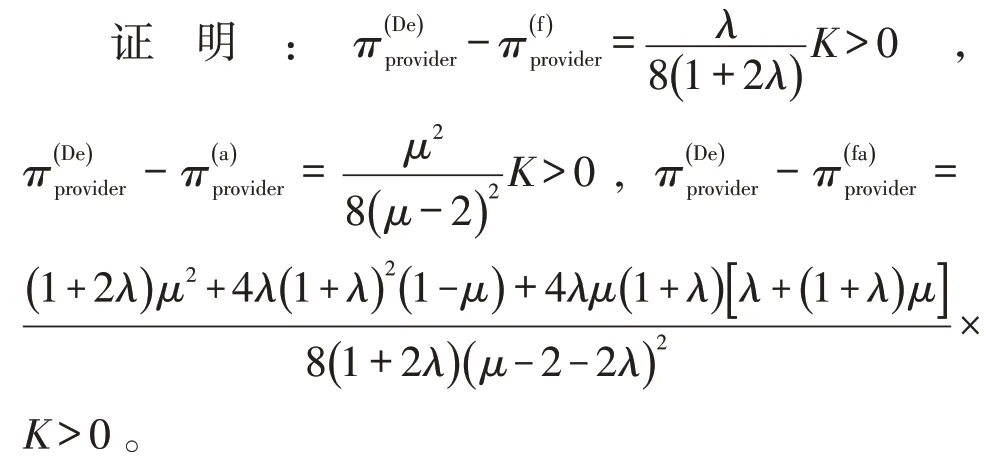
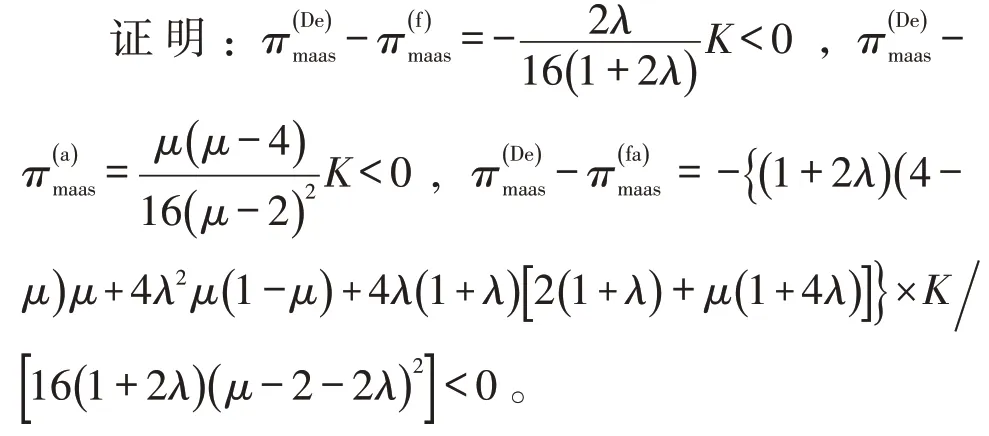
命题2～命题4 表明，分散决策模式下，不考虑决策者社会偏好时的最优批发价格高于考虑社会偏好时的价格，服务提供商的最优利润高于考虑社会偏好时的收益，然而，MaaS平台的最优收益低于考虑社会偏好时的收益。

命题5表明，服务链的整体最优收益在不考虑社会偏好时的合作决策模式下最大，在分散决策模式下最小（与仅考虑MaaS 平台不平等厌恶偏好下的收益相等），而利他决策模式下的服务链整体收益介于两者之间。

命题6 分散决策模式下决策者双方收益比较：

② 当0＜λ≤0.5 时，；否则，

③当0＜μ≤0.5 时，；否则，

④当0＜λ ＜0.5 且0＜μ ＜0.5 时，；否则，

证明：

3.2 社会偏好对决策变量的影响

由各决策者的决策变量和收益表达式对λ和μ分别求一阶导数，结果如表4所示。

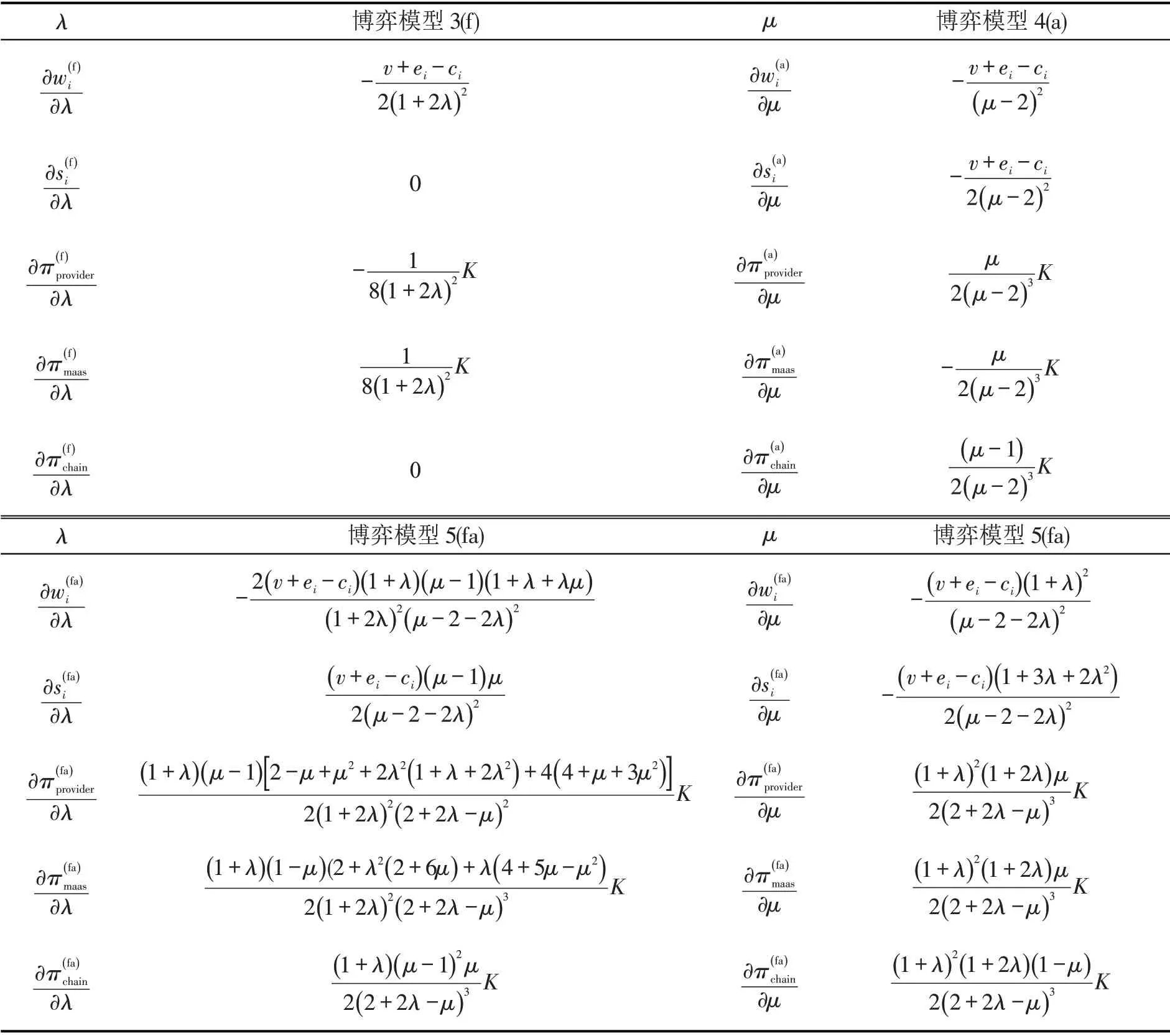
表4 决策变量的一阶导数解Table 4 First derivative solution of decision variables

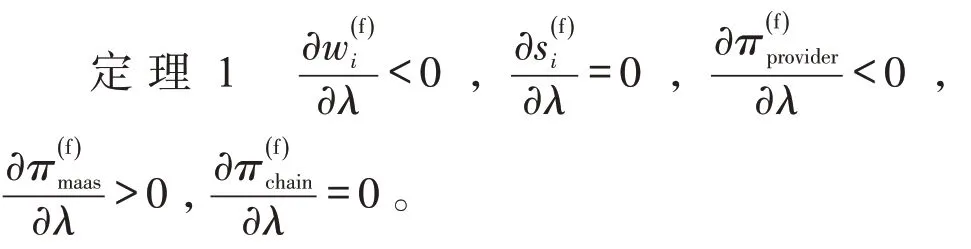
定理1表明，服务提供商的最优批发价格和最优收益，随MaaS 平台不平等厌恶偏好程度的增大而减小；MaaS 平台的最优销售价格与其自身不平等厌恶偏好无关，最优收益随其不平等厌恶偏好程度的增大而增大；服务链整体最优收益与无不平等厌恶偏好情形一致，不受MaaS 平台不平等厌恶偏好的影响。

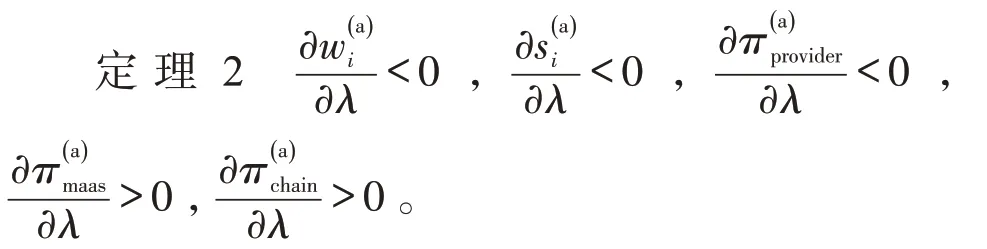
定理2 表明，服务提供商的最优批发价格、最优收益以及MaaS平台的最优销售价格均随服务提供商利他偏好程度的增大而减小；MaaS 平台的最优收益和服务链整体最优收益随服务提供商利他偏好程度的增大而增大。

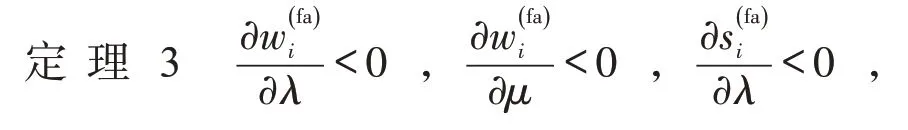
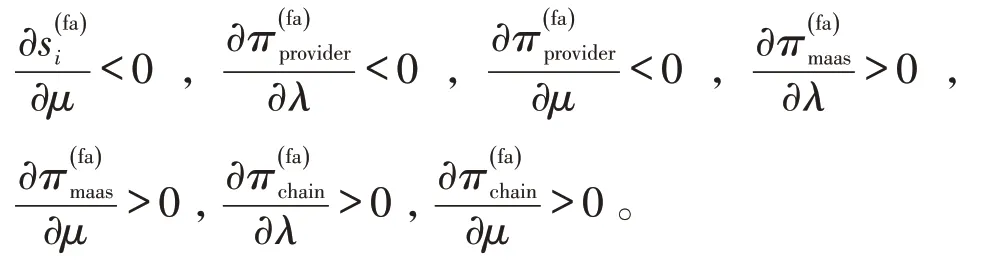
定理3 表明，当服务提供商具有利他偏好且MaaS 平台同时具有不平等厌恶偏好时，服务提供商的最优批发价格，MaaS 平台的最优销售价格以及服务提供商的最优收益均随服务提供商利他偏好和MaaS 平台不平等厌恶偏好的增大而减小；MaaS 平台最优收益随服务提供商利他偏好和MaaS平台不平等厌恶偏好的增大而增大。

4 数值分析

为直观地显示推导出的一些结论，本文通过数值算例进行验证分析，分析MaaS 平台不公平厌恶存在，服务提供商利他偏好存在以及MaaS 平台不平等厌恶且服务提供商利他偏好同时存在的3 种情形，探讨社会偏好对零售价格、批发价格、市场需求、服务链整体收益以及服务提供商和MaaS 平台收益的影响。

为不失一般性，选取2 种包日MaaS 套餐进行分析，分别为单方式旅游出行服务套餐和多方式旅游出行服务套餐，对基本常量进行赋值，具体为：

①v为2种套餐的基本效用，对于包日旅游出行服务套餐，其基本效用相同，取v=20；

②e为2 种套餐的实际体验，其中，多方式旅游出行服务套餐的体验高于单方式旅游出行服务套餐，取e1=30，e2=100；

③c为套餐成本，其中，多方式旅游出行服务套餐的成本高于单方式旅游出行服务成本，取c1=20，c2=40。

不考虑决策者社会偏好时的均衡解如表5所示。

表5 基本决策模式下最优定价策略及收益（1-2）Table 5 Optimal pricing strategy and profit in basic decision cases（1-2）

结果表明，均衡解均符合理论假设，决策权的分散导致旅游出行服务产品的销售价格和供应链整体最优利润降低，市场需求增加。

通过仿真模拟3 种情况下决策者的社会偏好弹性与决策变量，可以得出由社会偏好弹性变化的分析结果。MaaS平台的不平等厌恶偏好能够调节旅游出行服务链的收益分配，作为主导者的服务提供商的利他偏好也是十分重要的促进服务链协调的因素。

如图3所示，考虑处于主导地位的服务提供商的利他偏好或处于从属地位的MaaS平台的不平等厌恶偏好时，服务提供商将会以降低批发价格的方式提高服务链整体利润并使平台获得更多的服务链利润，从而有效维护服务链的合作关系。

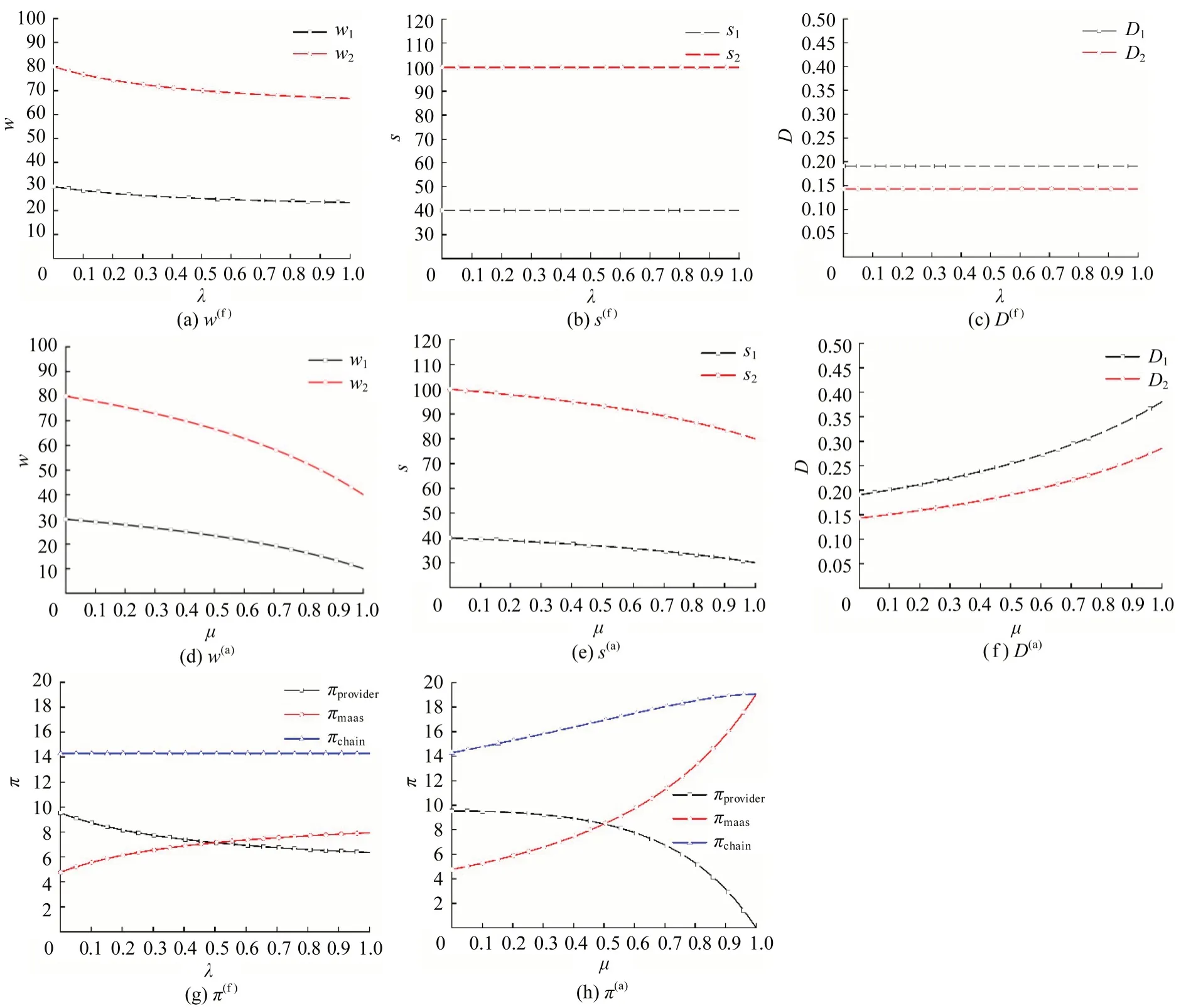
图3 博弈模型最优定价策略及收益（3-4）Fig.3 Optimal-pricing strategy and profit in game cases（3-4）

MaaS平台的不平等厌恶偏好程度与旅游出行服务产品的批发价格成反比，销售价格和市场需求不会发生变化，如图3（a）～图3（c）所示。服务提供商的利他偏好程度与产品的批发价格和销售价格成反比，销售价格的减少意味着出行者效用的增加，相应地，市场需求随之增加，如图3（d）～图3（f）所示。随着MaaS平台的不平等厌恶偏好程度不断增大，服务提供商的利润降低，而MaaS平台的利润增加，旅游出行供应链整体利润保持不变，其中，当0＜λ≤0.5 时，有；λ ＞0.5 时，有，如图3 （g）所示。随着服务提供商的利他偏好程度不断增大，服务提供商的利润逐渐降低，MaaS平台和服务链整体的利润逐渐增大，如图3（h）所示。当μ=1 时，批发价格降至成本价，，服务链整体最优收益达到合作决策模式下的结果。考虑决策者双方社会福利综合偏好时的均衡解如图4所示。

图4 博弈模型最优定价策略及收益（5）Fig.4 Optimalpricing strategy and profit in game case（5）

结果表明，旅游出行服务产品的批发价格和销售价格是决策者社会偏好程度的减函数，但销售价格随着MaaS平台不平等厌恶偏好的增加而减少的幅度较小，如图4（a）～图4（d）所示。旅游出行服务产品的市场需求是服务提供商利他偏好的增函数，但套餐1的市场需求随着MaaS平台不平等厌恶偏好的增加而减少，套餐2 的市场需求则与之相反，如图4（e）和图4（f）所示。随着决策者的社会偏好程度越强，服务提供商的最优收益逐渐减少，MaaS平台的最优收益逐渐增加，但服务链整体最优收益随利他偏好程度的增加而增加，随不平等厌恶偏好程度的增加而减少，如图4（g）～图4（i）所示。

5 结论

本文研究了MaaS 环境下，考虑决策者社会偏好特征的旅游出行服务产品的定价策略及服务链收益问题。建立Stackelberg博弈模型，比较分析不同博弈模型在旅游出行服务产品的批发价格、销售价格、市场需求、决策者收益和服务链整体收益，揭示内部规律，并模拟分析各最优决策变量的敏感性。研究得出如下结论。

（1）不考虑决策者社会偏好时，决策权的分散导致旅游出行服务产品的销售价格和服务链整体最优收益降低，市场需求增加。

（2）考虑决策者自身社会偏好存在时，随着MaaS 平台的不平等厌恶偏好程度增大，旅游出行服务产品的最优销售价格不受影响，服务链整体利润不变；随着服务提供商利他偏好程度的不断增大，服务提供商收益降低的幅度小于MaaS 平台收益增加的幅度，服务链整体最优收益不断上升；社会福利综合决策模式下，决策者双方社会偏好同时存在时，各最优决策变量受服务提供商利他偏好的影响程度大于MaaS平台的不平等厌恶偏好。

（3）为了优化旅游出行服务链运作，提升整体收益，处于跟随地位的MaaS 平台应选择具有利他偏好的服务提供商进行合作，或在与处于强势地位的服务提供商合作时，积极表达对服务链收益分配的不平等厌恶；处于主导地位的服务提供商应以服务链整体收益最大化和服务链协调为目标与MaaS平台开展合作，主动采取利他行为。