无信控路段人行横道处行人过街建模与仿真

陈鹏，唐鹏，闫伟曦，孙秋月

（1.武汉理工大学，交通与物流工程学院，武汉 430063；2.中交第二公路勘察设计研究院有限公司，武汉 430056）

0 引言

在无信控路段人行横道处，由于交通信号的缺位及交通系统的复杂性，行人的过街安全一直未能得到充分保障。针对无信控路段行人过街行为，现有相关研究主要注重分析影响行人过街行为的潜在因素（例如，手机[1]和路段类型[2]等），而且局限于描述行人过街速度[3]和间隙接受[4]等微观行为特性，然而，根据现实情况可知，仅从微观层面难以全面系统性地描述行人过街行为，因为，在面对不同的场景时，行人将从战略层、战术层和操作层这3 个层级做出相应的决策[5]，例如，孔德璇[6]利用决策层-战术层双层次交通行为的社会力模型描述机场旅客的离港行为，LI 等[7]建立操作层面的绕行社会力模型和战术层面的路径决策模型描述行人的绕行行为，研究结果均表明，对行人行为进行分层分析能更好地描述行人的行为特征。

针对行人过街决策问题，现有相关研究[8]往往只是分析行人在路侧情境下的决策模型，对于描述行人的违章过街行为较为有效，但是，对于无信控人行横道处行人的过街行为，由于行人存在分步决策的行为特性，所以，应当根据不同交通场景对行人的过街决策行为展开相应研究。针对行人微观运动模型，现有研究多集中于行人疏散行为建模分析[9]，而且局限于描述行人的微观运动行为，例如，行人的相互挤压[10]、加减速行为和避让绕行[11]等，缺乏无信控路段场景下相关环境（例如，对向行人和人行横道等）对行人过街微观行为的影响分析。

因此，针对上述研究中存在的问题，本文拟根据行人过街行为层次分析的结果，对行人过街行为，从行人过街决策和行人微观运动两方面进行分层建模分析。在战术层面，分别研究行人在路侧和路中场景下的过街决策行为；在操作层面，根据行人间的对向避让行为特性引入主动避让力，同时，引入人行横道对行人作用力的概念，建立基于改进社会力模型的行人微观运动模型。最后，在上述两个层面模型的基础上，实现无信控人行横道处行人过街双层模型仿真。

1 行人过街行为的双层模型架构

本文在HOOGENDOOM 等[5]提出的行人行为一般框架的基础上，探讨行人过街行为的理论框架。在人行横道处，行人根据不同交通场景按照战略层、战术层和操作层这3 个层级做出相应的决策。其中，战略层是行人行为活动的起点，包括出发时间选择和活动模式选择等，由于本文主要关注行人的过街行为，因此，行人在战略层的决策可以假定是已知的；战术层主要关注行人过街的决策行为，即行人在特定条件下是否过街；操作层主要关注行人过街的微观运动行为，例如，行人过街过程中的加速、减速及转向等微观动作。因此，本文建立的行人过街双层模型主要包括战术层面的行人过街行为决策模型和操作层面的行人过街微观运动模型，模型的具体架构如图1所示。

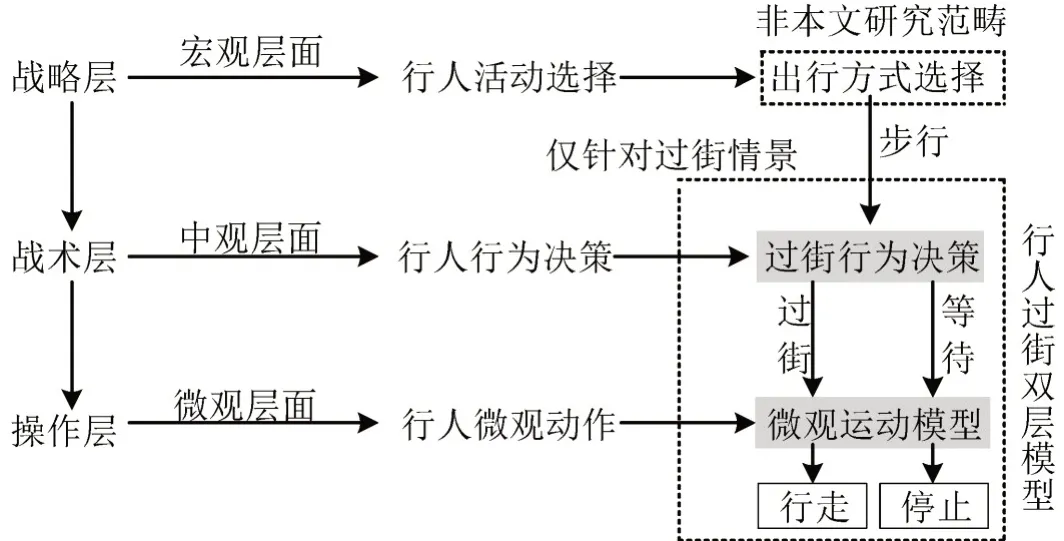
图1 行人过街行为双层模型架构Fig.1 Bi-level model structure of pedestrian crossing behavior

2 行人过街行为决策

2.1 行人过街决策行为分析

当行人通过车流量较大的无信控路段时，由于无信控路段多为双向2车道和双向4车道的路段形式，不同于多车道（车道数大于等于6）的滚动过街（即行人每跨越1 个车道便进行判断的过街模式），行人常在路侧和路中等待过街，即采取路侧和路中分步决策的方式选择过街行为，而且，当过街行人身处路侧和路中两种不同的交通环境中，行人过街决策所关注的重点会有所不同[12]。在路侧场景下，行人的心情较为平和，忍耐程度更高，过街的迫切性不高；在路中场景时，过街行人时刻暴露在与机动车碰撞的风险中，过街决策考虑的因素会更全面和谨慎，对于车辆的距离和速度等因素会更敏感。现有相关研究只考虑行人在路侧的过街决策结果，忽略了行人在路中环境下的决策情况，因此，有必要对路侧和路中两种交通场景下行人的过街决策行为分别开展相应的研究和分析。行人过街决策流程如图2所示。

图2 行人过街决策过程Fig.2 Decision process of pedestrian crossing

2.2 过街决策影响因素分析

（1）影响因素初步选取

本文调查对象为无信号控制人行横道处的过街行人及路段上车辆的运行情况，主要选取了两个无信控人行横道，数据分两次调查，每次调查时间为1 h，调查时间段为17:00-18:00，调查地点具体情况如表1所示。

表1 调查地点基本信息表Table 1 Basic information of survey location

经过剔除无效和错误数据后，本次调查共采集到1558 条有效数据，其中，行人路侧决策数据784条，行人路中决策数据774 条，相关数据信息描述如表2所示。

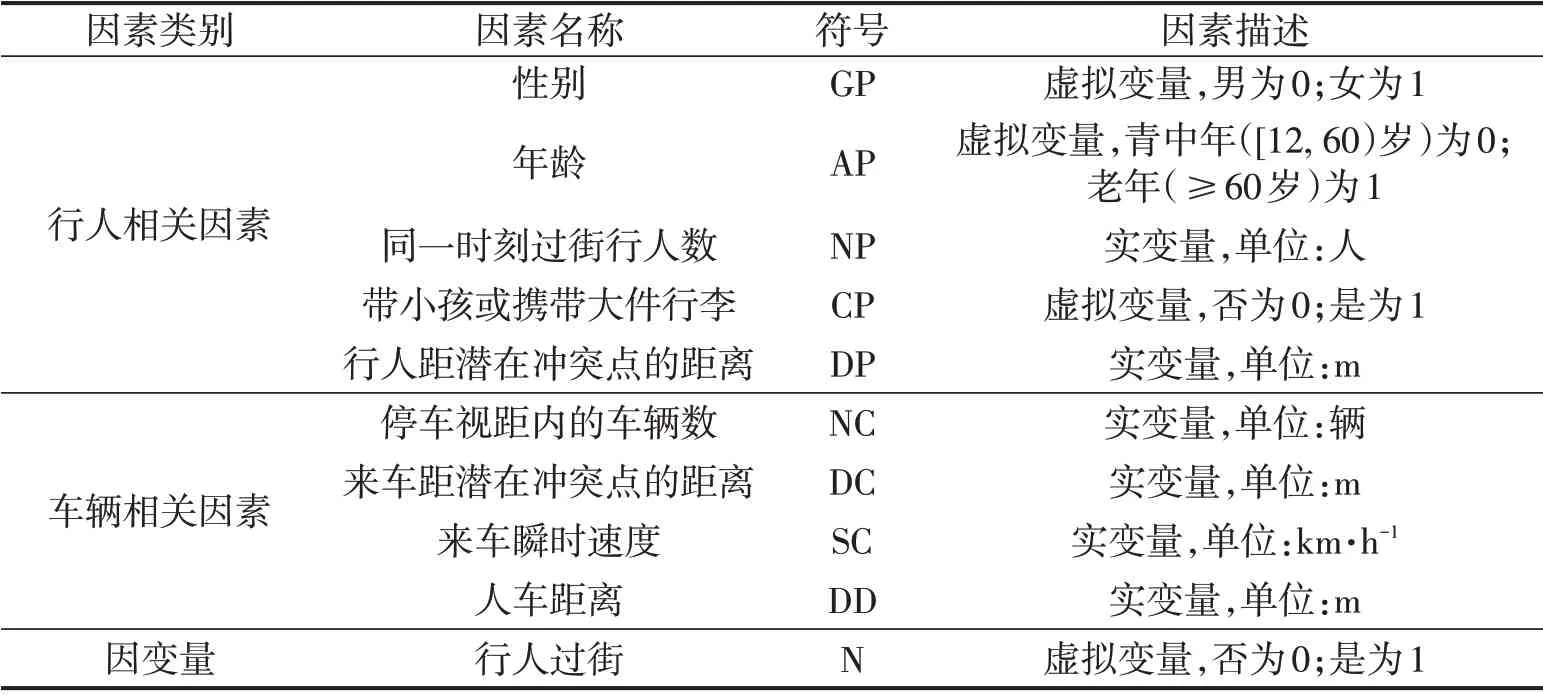
表2 数据采集信息描述表Table 2 Description of data information

（2）影响因素检验

考虑到上述因素中可能存在冗余因素，所以，需要对影响因素进行相关性检验。由于影响因素中包含多种类型的数据，所以，本文选择Spearman秩相关系数检验不同影响因素和行人过街决策结果之间的相关性，计算公式为

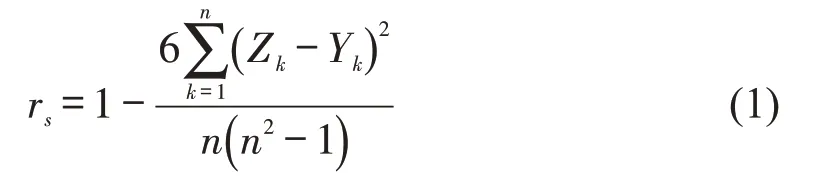
式中：n为数据点的个数；Zk为影响因素第k个数据的秩次；Yk为行人决策结果第k个数据的秩次。

利用SPSS 软件进行计算，计算结果如表3所示。

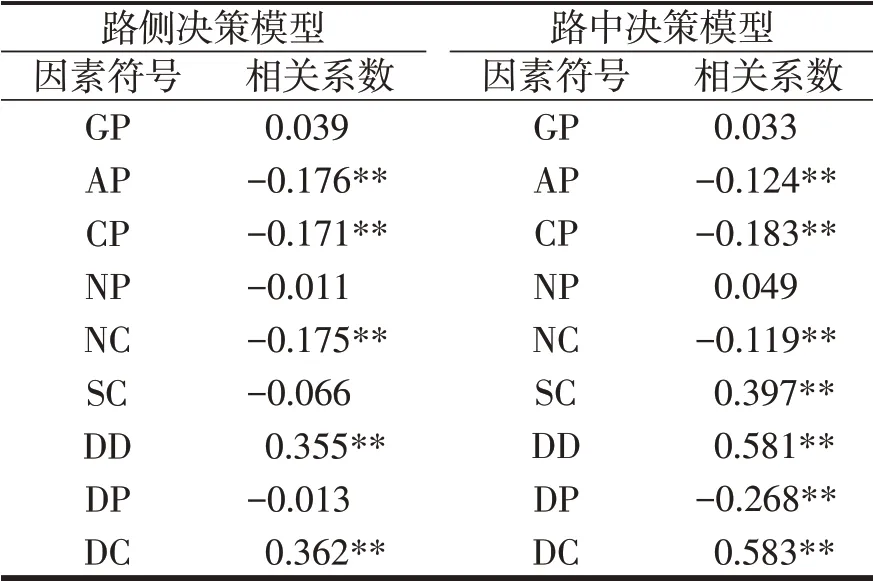
表3 相关系数计算结果Table 3 Calculation results of correlation coefficient

由表3结果可知，对于路侧决策模型，因素GP、NP、SC 和DP 与行人过街决策结果相关性不显著；对于路中决策模型，因素GP和NP与行人过街决策结果相关性不显著。在最终进行模型拟合时，优先考虑将上述因素剔除再进行相关分析。

2.3 行人过街决策模型建立

考虑到行人过街决策的结果是一个二分类变量，所以，本文选择二元Logistic回归模型拟合行人过街决策模型，公式为

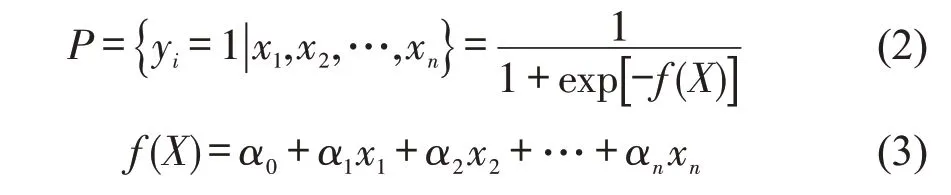
式中：P为行人过街的概率；yi为第i个行人的行为，yi=1表示行人过街，yi=0 表示行人等待；xn为第n个影响因素；X为影响因素的集合；α0为常数项；αn为回归系数。

以全部数据的70%作为拟合样本，剩下的30%作为检验样本，利用SPSS 软件对模型进行回归拟合，根据表3 影响因素的检验结果，将与因变量相关性较弱的自变量依次剔除后对模型进行拟合比较，选取拟合效果最好的模型作为最终模型，其中，最终模型的预测精度如表4所示。

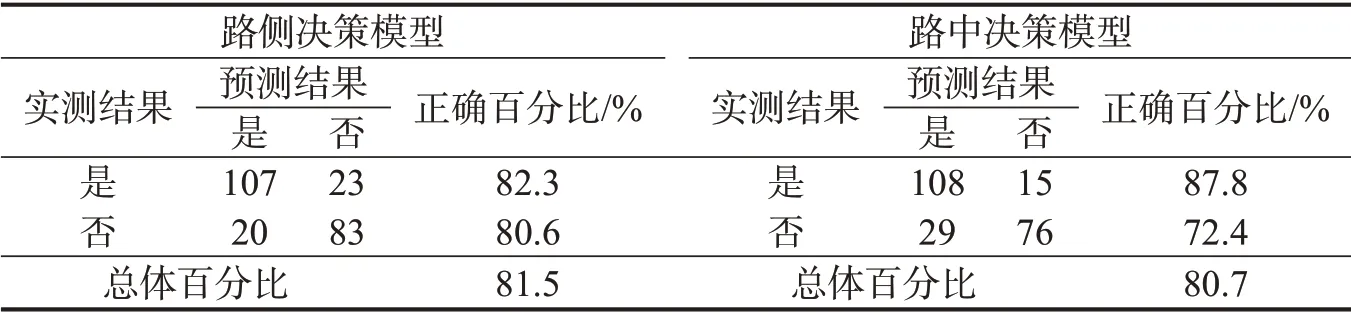
表4 拟合模型预测精度Table 4 Prediction accuracy of fitting model

路侧决策模型和路中决策模型预测准确率分别为81.5%和80.7%，说明最终拟合模型能较为准确地预测行人是否过街。最终模型的参数标定如表5所示。

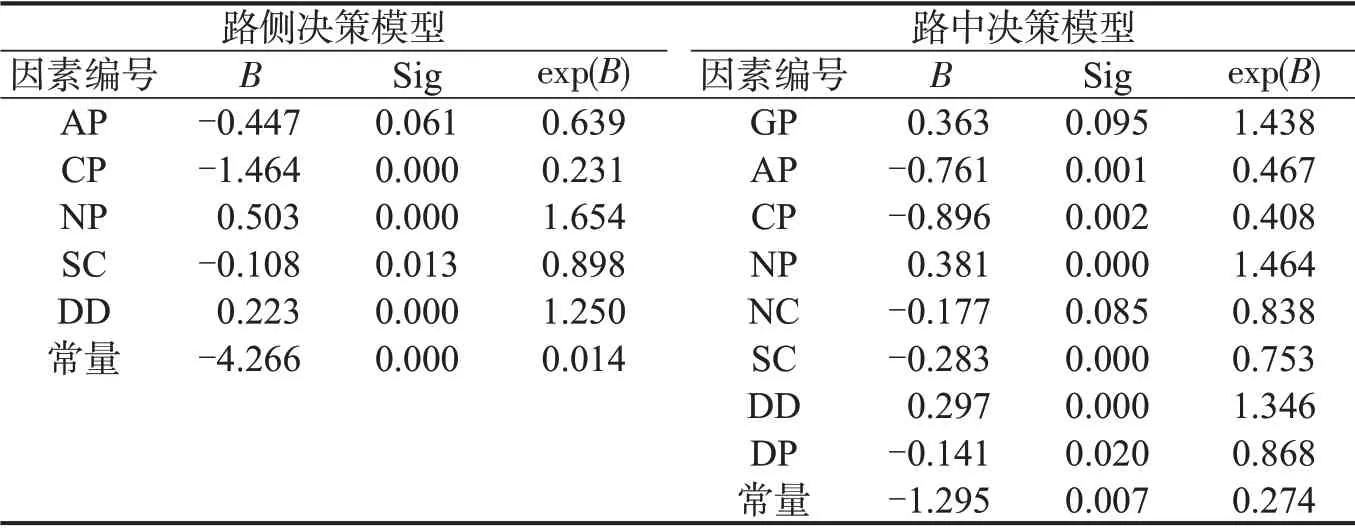
表5 模型参数标定结果Table 5 Calibration results of model parameters

路侧决策模型考虑因素主要包括：行人年龄（AP），行人是否带小孩或携带重物（CP），同一时刻过街人数（NP），来车速度（SC）及人车距离（DD）；路中决策模型在路侧决策模型考虑的因素上，还考虑了行人性别（GP），停车视距内的车辆数（NC）及行人距潜在冲突点的距离（DP）这3个因素，说明当过街行人处于道路中央驻足区或安全岛时，其过街决策时会考虑更多的因素。

3 行人过街微观运动

在过街过程中，行人由于受到自身及外界环境（例如，其他交通参与者和道路设施等）的影响，其微观行为复杂多变，考虑到行人行为的连贯性，本文利用社会力模型建立行人过街微观运动模型。

3.1 传统社会力模型

在传统的社会力模型中，个体一般会受到3种力的作用：个体自身驱动力、行人之间作用力及行人与障碍物（边界）作用力，受力方程简化为

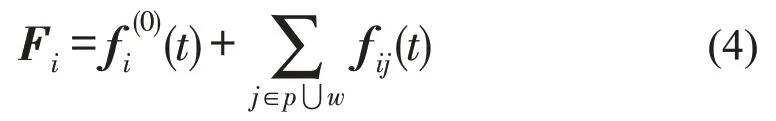
式中：f（0）i（t）为行人i自驱力；fij（t）为行人i与其他行人或障碍物（边界）的作用力；j为其他行人（p）和障碍物（边界）（w）的集合。

其中，行人自驱力方程为

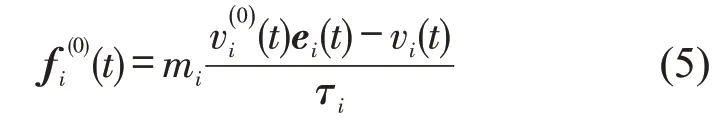
式中：mi为行人i的质量；（t）为行人i在t时刻的自身期望速率；ei（t）为行人i的目标方向；vi（t）为行人i在t时刻的实际运动速度；τi为反应时间。

行人与其他行人或障碍物（边界）的作用力方程为

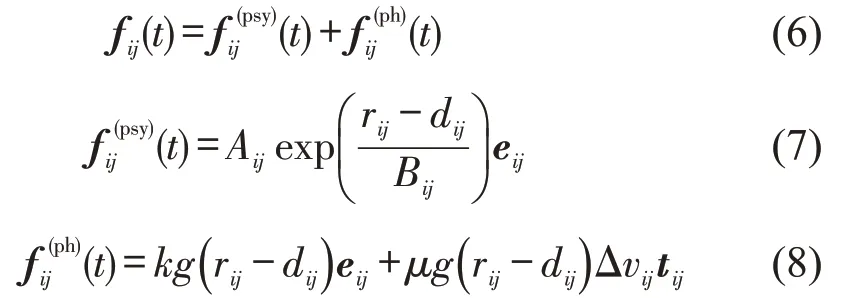
式中：为行人i与j之间的心理排斥力；为行人i与j之间物理接触力；Aij为排斥强度因子；Bij为排斥力作用范围；当j为其他行人时，rij为行人i和行人j的半径之和，当j为障碍物（边界）时，rij仅为行人i的半径；dij为行人i与j之间的距离；eij为行人i指向j的单位矢量；k为压力系数；g为重力加速度，取9.8 N·kg-1；μ为滑动摩擦力系数；Δvij为速率差；tij为切向单位向量，方向垂直于eij。

3.2 基于对向避让的行人自驱力模型改进

（1）行人对向避让行为特性

传统社会力模型虽然可以再现对向行人流中的成行现象，但是会产生一些不合理的挤压碰撞现象。当行人i和行人j其目的地分别为B和A时，在不受其他外力的作用下，行人i和行人j将会迎面相向运动，并且在行人自驱力和行人间作用力的合力下，行人间距离不断缩短，最终出现不合理的挤压碰撞现象，如图3所示。

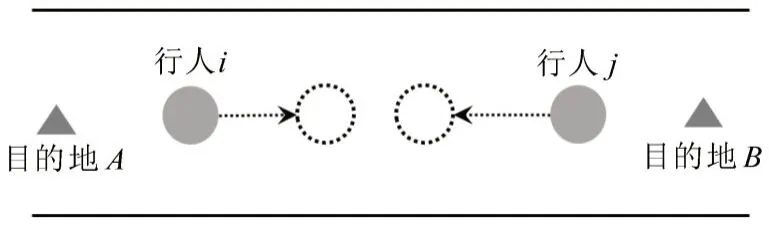
图3 传统社会力模型中行人迎面运动示意Fig.3 Schematic diagram of pedestrian opposite movement in traditional social force model

然而，在现实情况中，当面临上述情况时，行人并不都会按照现有的运动方向行进，其会临时改变运动方向，从而实现对向行人之间的相互绕行。行人间的对向避让行为参考以往相关研究可以分为避让偏移阶段、避让阶段和避让结束阶段[13]。对向避让行为如图4所示，其中，3个阶段的划分以行人i的运动轨迹为标准。

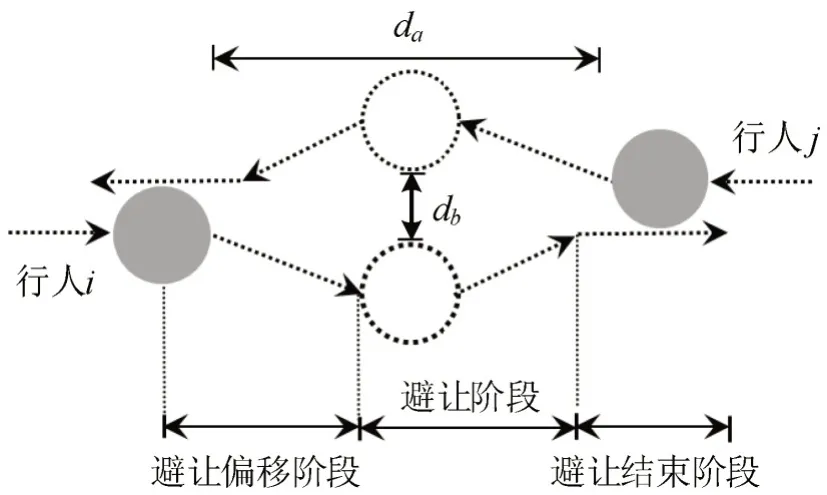
图4 行人对向避让示意Fig.4 Schematic diagram of pedestrian opposite avoidance

基于本文的实地调查数据，选取存在对向避让行为的行人，并根据提取的行人运动轨迹信息，统计对向避让时行人的距离特征，其中，重点分析避让偏移阶段开始避让时行人间的距离和避让阶段行人间的最小横向距离，结果如表6所示。

表6 行人对向避让行为距离特征Table 6 Distance characteristics of pedestrian opposite avoidance behavior

（2）主动避让力

基于传统社会力模型中对向行人间作用力描述不明确的问题，同时，考虑现有研究中忽略了行人速度参数[13]，为了更好地体现行人在不同速度下避让对向行人的强烈程度，本文在驱动力基础上，引入主动避让力的概念，描述对向行人间的提前避让行为，改进后的驱动力为自驱动力与主动避让力之和，即

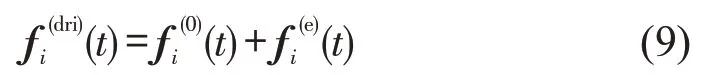
式中：为行人驱动力；为行人i主动避让力。

行人主动避让力产生的前提是对向行人间存在冲突，因此，在计算主动避让力时，需先进行冲突点的有效性判断，在冲突点被判定有效后，考虑行人右行偏好，以有效冲突点为垂足向右侧重新建立临时目的地。为方便说明，以对向行人间连线的平行方向为x轴，则行人主动避让力受力情况如图5所示。

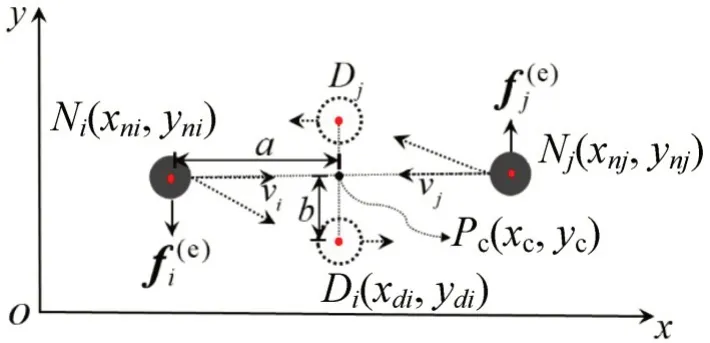
图5 行人主动避让力示意Fig.5 Schematic diagram of pedestrian active avoidance force

由于行人目标位置发生变化，因此，主动避让力可参考驱动力的方法进行计算，即

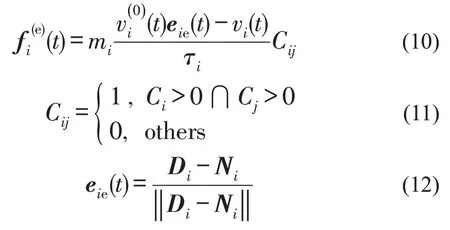
式中：eie（t）为行人i新的目标方向；Cij为行人间冲突有效性判定机制；Ci（Cj）为行人i（j）到达潜在冲突点所需时间，当Ci和Cj都大于0 时，行人i和行人j均暂未通过潜在冲突点，且都在朝着冲突点行进，故这种情况为有效冲突，而对于其他情况，则是无效冲突；Ni、Nj分别为行人i、j当前位置坐标；Pc为行人i、j间潜在冲突点的坐标，其中，Di为行人i新目的地的位置坐标，其中，xdi=xni+a，a为行人i提前避让距离，，ydi=yni-b，b为行人i横向避让距离，

3.3 基于人行横道的行人与边界作用力模型改进

（1）行人过街轨迹分布特性

行人过街的过程中，由于受到多种因素的影响，其运动轨迹会不断发生变化。为分析行人过街的轨迹分布情况，以行车道的平行方向截取人行横道纵向截面，其中，杨园南路和中山路截面间距分别为2 m，3 m，分析其轨迹点横向分布情况，结果如图6 所示。其中，实心点表示均值，上下短线表示横向分布15%～85%的区间范围，即下短线表示有15%的轨迹点横向坐标小于该值，上短线表示有85%的轨迹点横向坐标小于该值。

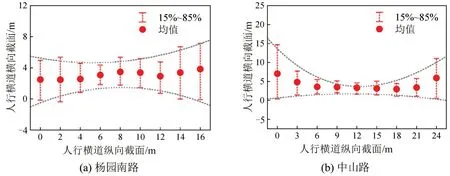
图6 过街行人轨迹点横纵分布Fig.6 Horizontal and vertical distribution of pedestrian crossing track points

由图6可知，在人行横道两侧行人轨迹点的横向分布波动范围较大，但是，随着过街进程的推进，其波动范围会逐渐缩小，过街行人会倾向于在人行横道内行走，由此可以认为人行横道边界线对行人运动产生了力的作用，迫使在人行横道外的行人逐渐向人行横道方向运动，而且这种力的大小在道路中央更为显著，所以，有必要分析人行横道对于行人过街行为的影响。

（2）模型改进

当行人在过街时，由于人行横道内不存在墙壁和栅栏等硬边界，通过上述对行人过街轨迹分布特性分析可知，人行横道边界对过街行人存在作用力的影响，但是，人行横道边界不同于墙壁等硬质边界，它是一种虚拟边界，故不存在类似于行人与硬质障碍物之间存在的法向挤压力和切向摩擦力，其对行人的作用力主要还是类似于一种心理作用力，因此，在传统社会力模型行人与障碍物边界心理排斥力的基础上，考虑到行人在靠近道路中线时受到人行横道的作用力单调递增，而在远离道路中线时约束力显著下降的特点，引入行人到道路路侧的距离因子，表征行人与道路中线的相对位置关系，因此，将人行横道对行人施加的作用力表述为

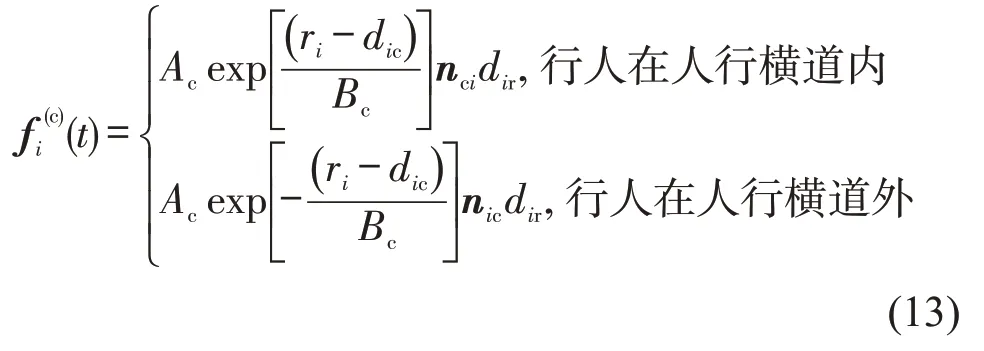
式中：dic为行人到边界的垂直距离；Ac和Bc为边界作用力强度和范围；当行人位于人行横道内时，nci为人行横道边界指向行人的单位向量；当行人踏出边界后，nic为由行人指向边界的单位向量；dir为行人到路侧的最短垂直距离。

人行横道边界的排斥力和吸引力如图7 所示。当行人j在人行横道外时，出于安全心理的考虑，行人会倾向于在人行横道区域范围内进行过街，这时人行横道对行人会呈现一种类似吸引力的效果，促使行人进入人行横道范围；当行人i在人行横道内时，人行横道对行人会呈现一种类似排斥力的效果，当行人靠近人行横道边界时，边界会产生相应的排斥力使行人维持在人行横道内行走，而且该力随行人到边界的距离单调递减。

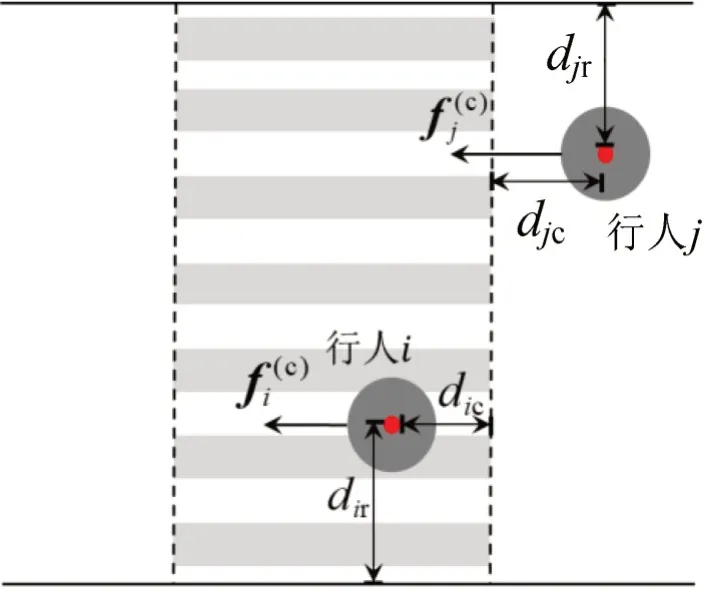
图7 人行横道边界的排斥力和吸引力Fig.7 Repulsive and attraction force of crosswalk boundary

3.4 过街行人社会力模型运动方程

本文基于改进的社会力模型构建行人过街操作层面的行人过街微观运动模型，改进的社会力模型主要是考虑传统模型不能很好地描述现实中对向行人间提前避让的情况，以及忽视了人行横道对于过街行人的影响。因此，在传统社会力模型的基础上，在行人的自身驱动力中引入主动避让力，同时，针对人行横道对过街行人的作用力进行更加详细地描述。

综合上述对传统社会力模型的修改，同时，考虑在人行横道处，行人几乎不受障碍物的影响，故行人与边界（或障碍物）作用力中只考虑人行横道对行人的作用力，则无信号控制人行横道处过街行人的社会力模型为

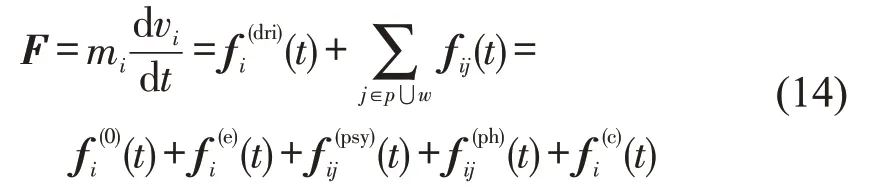
4 行人过街双层模型仿真

由于本文需要对行人和车辆进行混合仿真，而且行人运动依赖于改进的社会力模型，故本文选择AnyLogic 作为模型仿真平台。相较于其他软件，AnyLogic 最大的优势在于用户可以基于Java 自行搭建行人运动模型，并且可以自定义模型参数，非常适用于本文行人过街双层模型的仿真实现。行人过街双层模型中过街行人仿真流程如图8所示。

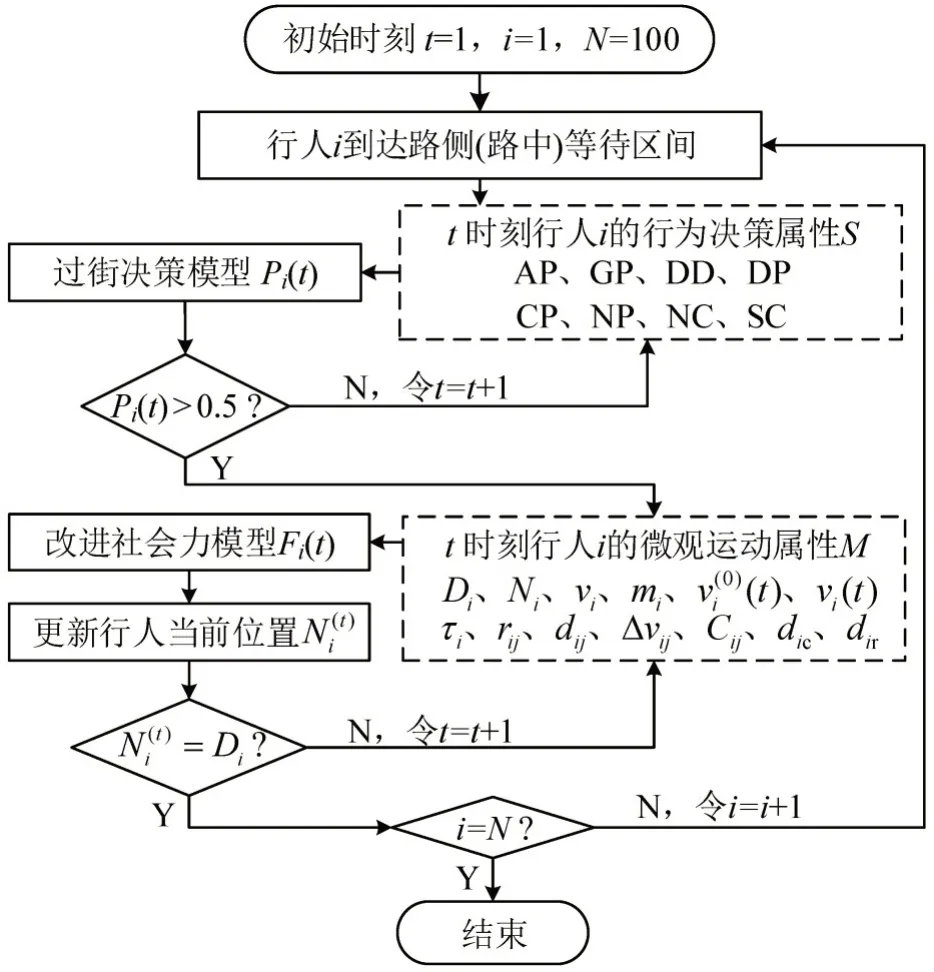
图8 过街行人仿真流程Fig.8 Simulation flow chart of pedestrian crossing

在进行仿真前，需标定模型参数，参数标定主要有两种方法：①参考现有研究成果；②依据对实际行人运动轨迹的观察，利用极大似然估计等统计学方法进行估计。由于模型中存在大量待标定的参数，如果所有参数通过极大似然估计法得到，数据计算量较大，故本文采用调查数据标定和文献结果标定相结合的方法标定模型参数，结果如表7所示。

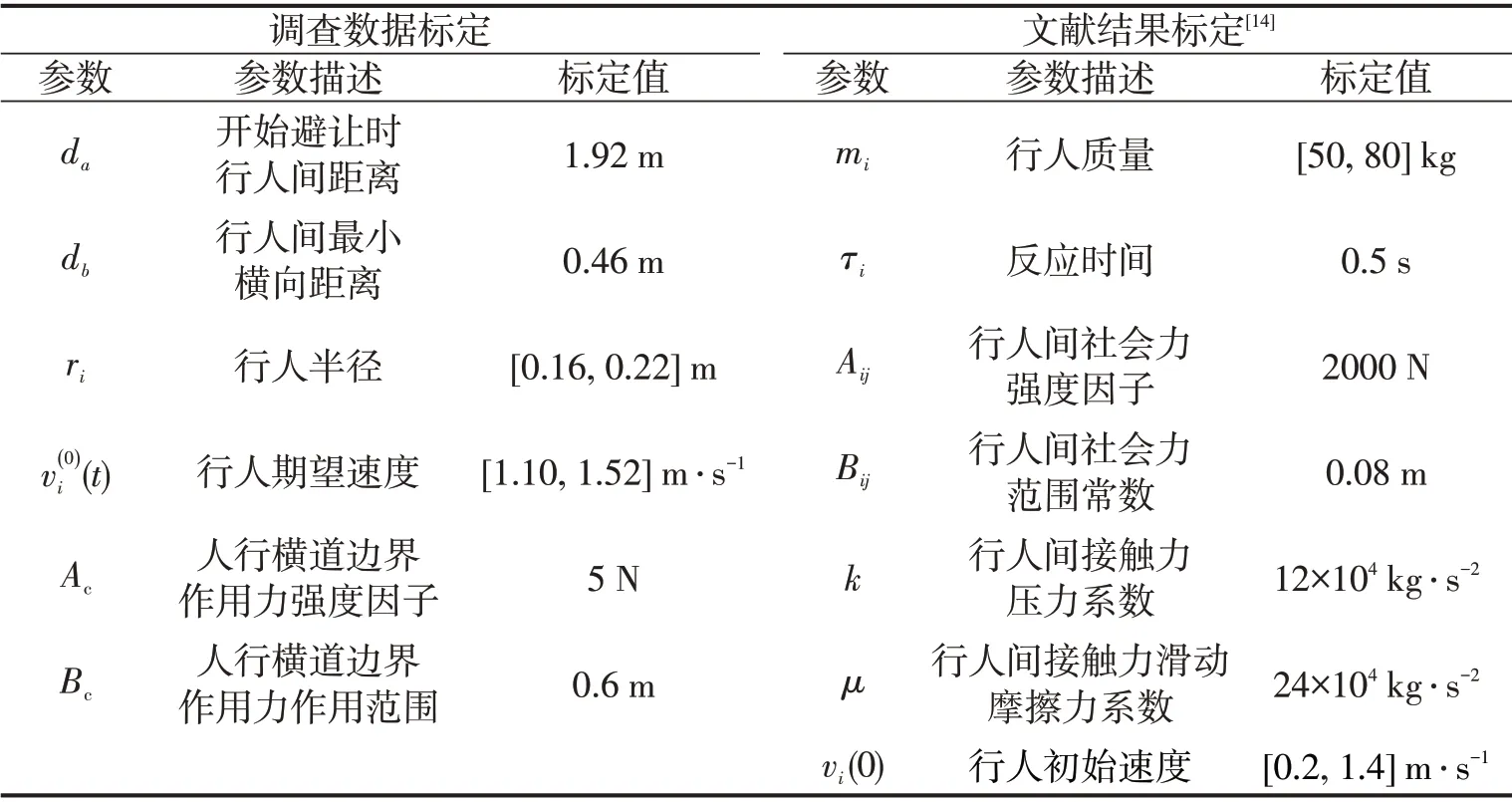
表7 模型参数标定结果汇总表Table 7 Summary of calibration results of model parameters

4.1 行人对向避让行为仿真分析

为验证引入行人主动避让力后模型的仿真效果，考虑到在人行横道场景下效果无法突出显示，因此，建立通道场景进行仿真对比。在AnyLogic软件中设置的比例尺为1∶10，即现实中的1 m对应软件中的10 pixel，其中，通道长度设置为200 pixel，宽度为20 pixel，行人分别以40 s 的时间间隔同时从两侧进入通道，分别记录每个行人的坐标并输出，其模拟过程如图9所示。

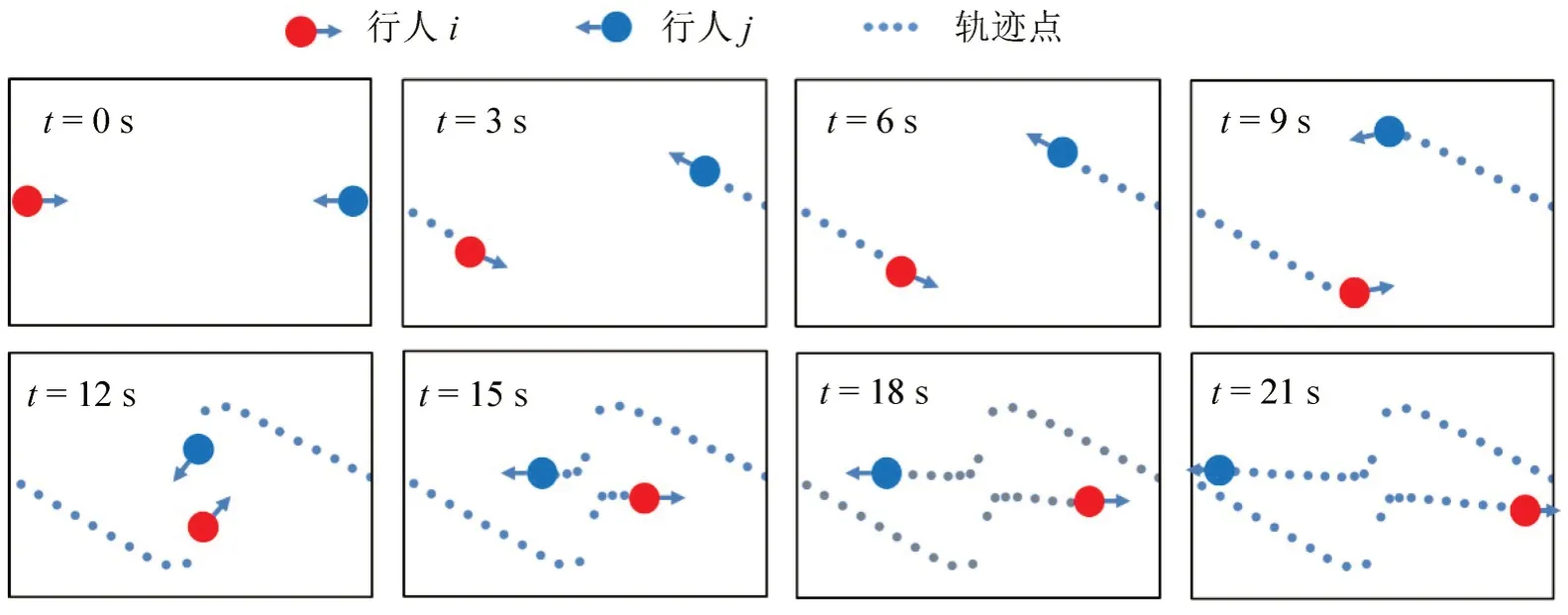
图9 行人对向避让仿真示意Fig.9 Simulation diagram of pedestrian opposite avoidance

为保证结果的可靠性，分别基于传统社会力模型和引入行人主动避让力后的改进社会力模型进行仿真，各收集50组行人的运动轨迹进行分析，如图10所示。

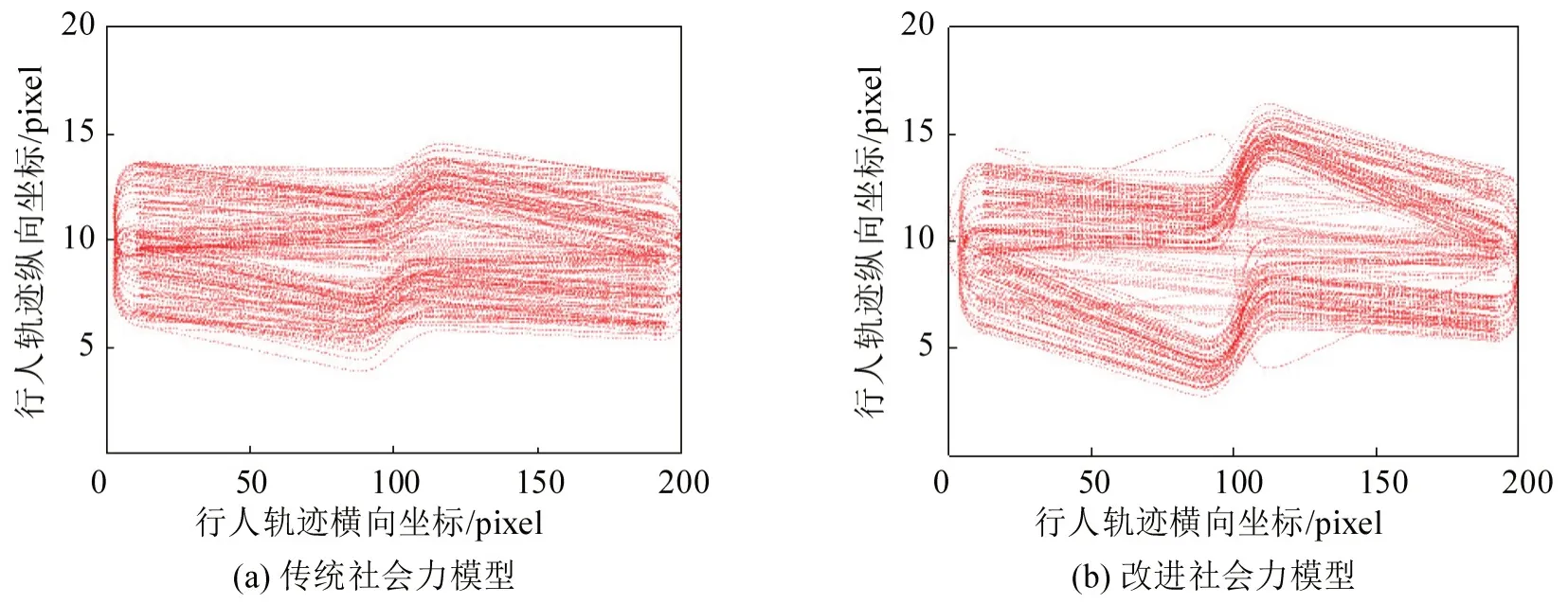
图10 行人对向避让轨迹仿真结果Fig.10 Simulation results of pedestrian opposite avoidance trajectory

由图10可知，在传统社会力模型中，由于行人间排斥力的作用，对向行人会对本向行人的运动轨迹产生轻微的影响，但是对向避让时行人间最小横向距离平均值为0.46 m，传统社会力模型仿真结果显然与实际情况不符，而引入行人主动避让力的改进社会力模型，很好地体现了行人间对向避让时的运动情况，从行人轨迹图可知，行人在与对向行人冲突时，会主动向右侧避让，在冲突点右侧[0.4,0.6]m 重设临时目标点，在对向避让结束后，行人重新回到原来的运动方向，与实际情况相符。

4.2 行人过街轨迹分布仿真分析

为进一步验证仿真模型的有效性，最佳方法是比较仿真轨迹与观测轨迹之间的差异，然而该方法过于主观且不精确，由于行人的行为具有极大的随机性，因此，无法将模拟轨迹和观察轨迹相互对应进行进一步的研究，只能从轨迹的整体分布规律进行分析。以杨园南路的无信控路段人行横道作为仿真建模对象进行相关研究，首先，以道路两侧边线及道路中线分别截取人行横道近、中、远端截面；然后，对穿越3 个截面的过街行人进行统计分析，行人穿越位置分布结果如图11所示。

由图11 可知，通过仿真得到的过街行人穿越位置分布规律与观测结果接近，利用两样本Kolmogorov-Smirnov（K-S）检验分布特性，将两样本分布函数之间的最大距离作为统计量D，表达式为

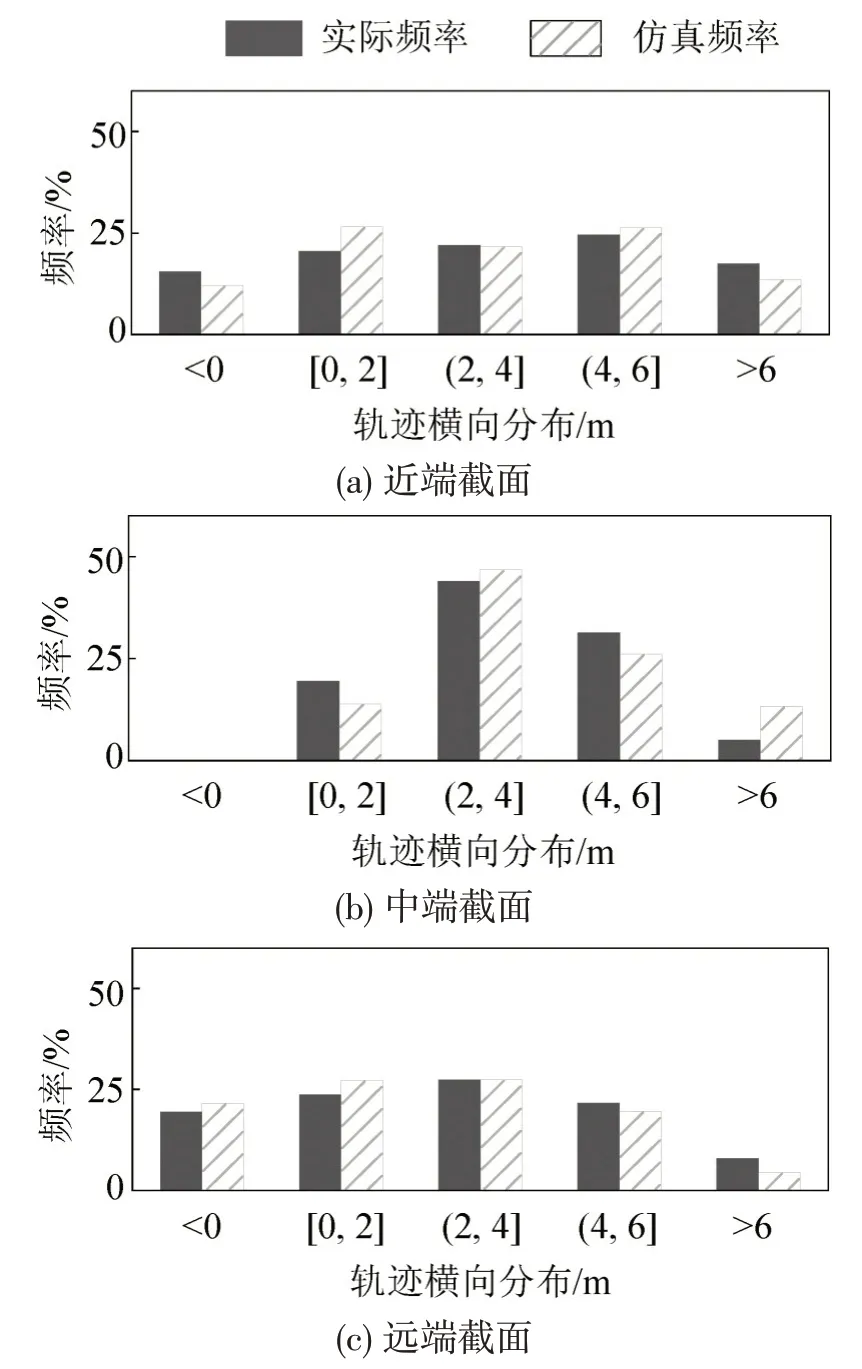
图11 行人穿越位置分布Fig.11 Pedestrian crossing location distribution

式中：R（x）和K（x）分别为两个样本的分布函数；m和l为上述两个样本的样本量；Dα为检验判断的临界值；α为显著性水平；c（α）一般取 -0.5 lnα。

原假设H0为：两个样本来自于分布相同的总体。当D ＞Dα时，则拒绝原假设；否则，说明假设成立。从统计结果可以看出，行人穿越位置分布的实测数据与仿真数据差异不大，采用两样本K-S对其进行检验，在0.01 显著性水平下，临界值Dα为0.215，利用SPSS 计算得到近、中、远端截面分布函数的D分别为0.044，0.107，0.060，均小于其临界值，因此，原假设成立，说明调查和仿真得到的行人穿越位置分布服从于同一分布。

此外，由图11 可知，在人行横道近端截面，行人倾向于在靠近人行横道两端的位置进入人行横道，在人行横道中端截面，行人穿越位置分布主要集中于人行横道的中间位置，而在人行横道远端，行人位置分布逐渐向两端扩散，主要是因为在人行横道两端人行横道对行人的作用力较小，而且，行人在靠近路侧时出于便捷心理，时常会出现行人溢出人行横道的现象出现，与现实情况相符。以上特征表明，所建立的改进社会力模型可以合理地反映人行横道上的行人行为特征。

5 结论

本文以武汉市无信控路段实际调查结果为基础，建立无信控路段人行横道处行人过街双层模型，所得主要结论如下：

（1）针对行人过街决策问题，采用分步决策更贴近实际情况，而且研究发现，路侧决策模型与路中决策模型所考虑的因素存在差异，主要区别在于路中决策模型考虑的因素更为全面，相较于路侧决策模型所考虑的因素，行人性别、停车视距内的车辆数和行人距潜在冲突点的距离这3 个因素对路中决策模型也存在显著影响。

（2）针对行人过街微观运动模型，与传统社会力模型相比，引入行人主动避让力能更好地反映行人在对向避让过程中的距离特征，同时，引入人行横道对行人作用力能更好地反映行人在人行横道内的轨迹分布情况。