面向新型混合交通流的智能交叉口网络布局优化

李同飞，曹雅宁，窦雪萍，熊杰，许琰，周文涵

（北京工业大学，交通工程北京市重点实验室，北京 100124）

0 引言

随着无线通信技术和车联网技术的发展，CAV已经是公认的未来车辆发展方向。然而，由于受技术发展水平、车辆价格以及接受度等因素的影响，短期内HV不会完全被CAV取代，未来较长时间内城市路网中将是由CAV 与HV 构成的新型混合交通流，这将颠覆当前的交通组织场景，给交通规划与管理者带来前所未有的挑战。

针对CAV 参与下的城市交通系统，以往的研究主要从路段行驶特性与组织、交叉口组织及网联自动驾驶场景下的城市路网这3 个层面展开。路段层面主要集中在对CAV的路段行驶特性进行研究，例如，研究CAV的跟驰行为、换道行为、超车行为及编队行驶等。针对CAV与HV混行的场景，相关研究主要聚焦于车辆在行驶过程中的交互[1]、车辆的速度轨迹及时空轨迹优化[2]等方面。

在交叉口组织层面，国内外学者针对网联自动驾驶环境下的交叉口控制策略展开了详细研究。针对单个交叉口，冯琦[3]从微观角度出发，研究车联网环境下车辆统一管理与控制，设计车辆通行规则和交叉口协调控制算法，实现冲突分离。针对多个连续信号交叉口，鹿应荣等[4]提出适用于CAV的连续信号交叉口控制方法，通过计算车辆连续通过下游多个交叉口的恒定运行速度，提出了车速调整策略，控制车辆平滑地通过多个交叉口。在全网联自动驾驶环境下，基于车辆全部为CAV 的假设，DRESNER等[5]提出一种基于预约的无信号交叉口协同控制机制，进入交叉口的车辆需提前向控制中心发送预约请求和接收通过时间间隙，并通过仿真模拟研究了预约策略与传统信号灯控制策略下的交叉口通行效率，发现前者是后者的2～3倍。在此基础上，HE等[6]提出一种可全向转弯的无变道自动控制交叉口，并考虑了全向转弯时交叉口内部冲突点增多和CAV 的速度特性，设计了基于冲突避免的控制方法，协调各方向来车。

在宏观路网层面，对CAV与HV混行的城市交通系统研究主要关注混行模式下出行者路径选择行为和CAV专用道规划布局等问题。基于LEVIN等[7]提出混合交通道路通行能力的研究，WANG等[8]考虑两类车辆不同的感知能力，建立了整合用户均衡和嵌套Logit 模型的多用户交通分配模型，研究混行模式下出行者路径选择行为。为减少两类车之间的干扰，充分发挥CAV的优势，并考虑减少道路资源的浪费，LIU 等[9]提出一种新的车道组织形式-CAV 专用收费车道，允许HV 支付一定费用在该专用道上行驶，并研究了普通CAV 专用道和CAV收费车道在路网上的部署问题。

得益于车-车通信（V2V）和车-路通信（V2I）等车联网技术以及自动驾驶技术，CAV可以采用智能交叉口的组织形式，不依赖灯色控制，通过车-车之间实时通信与协调控制，快速有序的通过交叉口，大大提高了交叉口的通行效率和通过能力。同时，为保障HV正常通行，传统视觉信号交叉口依然有存在的必要性。不同于微观层面的交叉口研究，本文从交通规划者的角度，针对新型混合交通流提出采用混合的交叉口组织形式，兼顾HV 出行可达性，提出智能交叉口网络布局优化问题；充分考虑两类车辆在两类交叉口的通行时间与通过特性差异，提出两类交叉口的通行时间计算公式；考虑两类出行者不同的路径选择行为，建立以系统最优为目标的智能交叉口网络布局优化模型，设计算法进行求解，并通过经典Sioux-Falls 网络作为案例分析，验证模型与算法的有效性。

1 混行模式下的城市交通系统与交叉口组织

1.1 新型混合交通流下的道路通行能力计算

CAV通过车-路侧设施-云端控制中心彼此之间的实时通信，与HV 在道路上混合行驶，组成新型混合交通流。相比于HV，CAV具有以下特性：第一，在路段层面，CAV反应时间更短，可以与前车保持更短的车头时距，从而提高道路的通行能力；第二，在路网层面，基于V2V、V2I及V2C等实时通信技术，CAV能够准确获取整个路网上的交通状态信息，准确选取最短路径出行。新型混合交通流如图1所示。

图1 新型混合交通流Fig.1 Novel mixed traffic flow

因此，根据CAV的第一个特性可知，混行模式下的道路通行能力不再是定值，而是与路段上CAV渗透率和车辆排列分布等因素相关的变量。基于LEVIN 等[7]对具有不同反应时间的车辆混行模式下的道路通行能力研究，并假设无论前车为何种车辆，跟驰车辆均具有相同的制动反应时间，给出混行条件下的道路通行能力计算公式。

令G（N,A）表示路网，其中，N表示节点集合，节点i∈N，路网中节点的数量为n；A表示路段集合，路段a∈A。

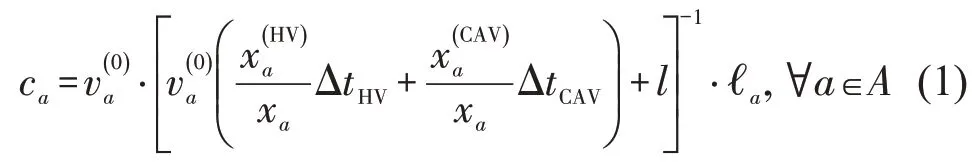
式中：ca为混合交通流下路段a的通行能力；为路段a上的自由流车速；xa为路段a上的总流量，分别为路段a上HV、CAV 的比例；ΔtHV、ΔtCAV分别为HV、CAV 出行者的反应时间；l为车身长度；ℓa为路段a的车道数量。

1.2 面向新型混合交通流的交叉口组织

通过图像识别技术、车辆与路侧基础设施通信技术及自动驾驶技术，CAV可以自主通过传统视觉信号交叉口。同时，CAV又可以采用智能交叉口的组织形式，即车辆在交叉口的通行不依赖灯色控制，依靠V2V 和V2I 实时通信，实现协同感知与速度控制，彼此配合，快速高效地通过交叉口。相比于传统视觉信号交叉口，智能交叉口的组织模式将极大地提高交叉口通行能力。

与此同时，由于缺乏相关技术支持，HV不能采用智能交叉口的组织形式，无法通过智能交叉口。为了保证HV在城市路网上的正常通行，传统视觉信号交叉口依然有存在的必要性。最终，在CAV与HV 混合行驶的城市交通系统中将会存在两类交叉口，即传统视觉信号交叉口和智能交叉口，如图2所示。

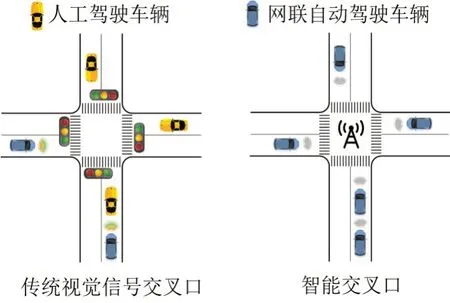
图2 面向新型混合交通流的两类交叉口组织Fig.2 Two types of intersection organization under novel mixed traffic flow

为避免HV 错误驶入智能交叉口引发安全风险和干扰CAV 的正常通行，需将驶入智能交叉口方向的信号灯始终设置为全红状态，禁止HV驶入智能交叉口所连接的路段，同时，在此处发布CAV可以通行的相位信号，允许其驶入智能交叉口连接的路段。面向新型混合交通流的交叉口规划布局如图3所示。

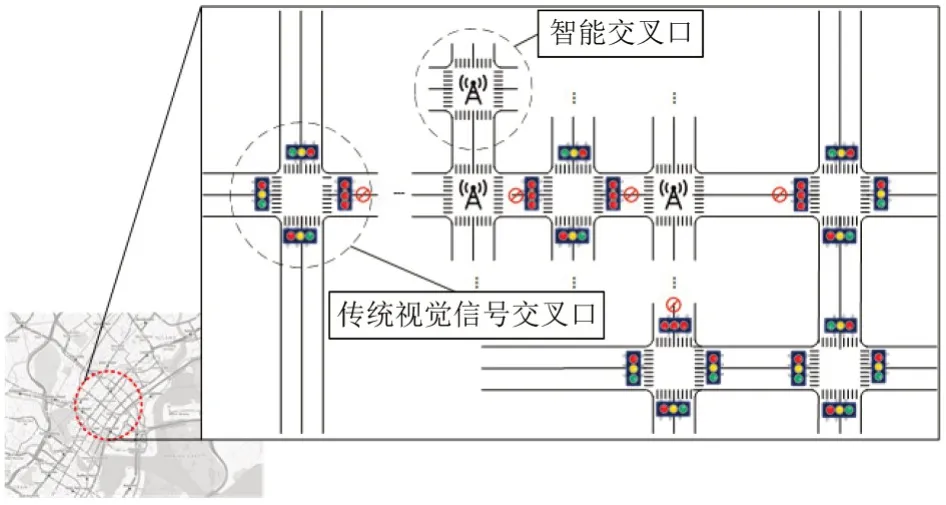
图3 面向新型混合交通流的交叉口规划布局示意Fig.3 Schematic diagram of intersection layout planning under novel mixed traffic flow

1.3 两类交叉口通行时间计算

CAV 可以通过图像识别等技术识别信号灯灯色，进而通过传统视觉信号交叉口。同时，在传统视觉信号控制交叉口，HV和CAV都依照信号灯色的指示，按照划分的相位有序通过交叉口，因此，两类车辆在此交叉口的通过时间认为是相同的。

同时，由于车辆的异质性，在对交叉口通行时间进行计算之前需要将混合交通量转化为标准交通量。具体地，根据交叉口行驶过程中CAV 对道路空间的占用，引入εHVE′表示交叉口处单位CAV流量等价为HV流量（即标准交通量）的折算系数[9]，将交叉口处混合交通量转换为等价的HV流量，该折算系数具体计算为

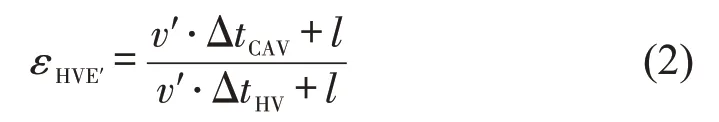
式中：v′为车辆在交叉口处的行驶速度。

基于Webster 等于1958年提出的信号交叉口延误模型，在所有车辆均匀到达的假设下，可以得到两类车辆在路段a下游传统视觉信号交叉口的通行时间为

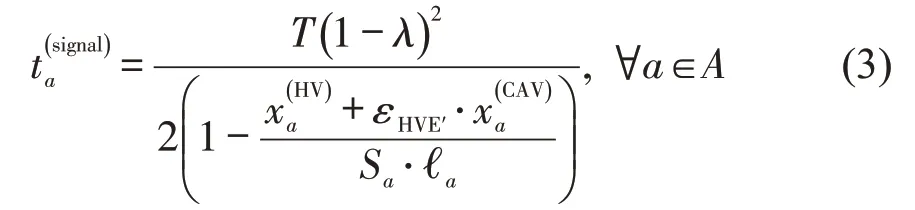
式中：T为交叉口周期时长；λ为绿信比；为交叉口处混合交通量转化成的等价HV流量；Sa为纯HV通行下，路段a上一条车道的饱和流率；ℓa为路段a的车道数量。为简化计算，认为所有视觉信号交叉口为两相位控制。

由于在智能交叉口所连接的路段可采用无车道划分的形式，CAV 可以自由变换车道，进行全向转弯[8]，故可采用1 个统一的值表示不分流向的节点阻抗。因此，CAV在路段a下游所连接的智能交叉口处通行时间为

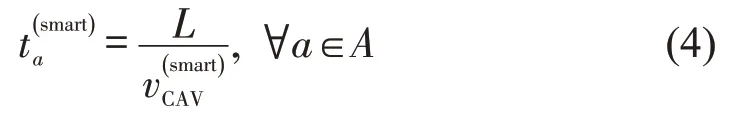
式中：L为交叉口的宽度；为CAV在智能交叉口内部的平均车速。

2 新型混合交通流的网络均衡问题

为描述新型混合交通流下CAV 与HV 的路径选择行为，建立新型混行模式下混合用户均衡模型。

2.1 出行时间计算

（1）路段出行时间

在新型混合交通流下的路段通行能力计算基础上，新型混合交通流在路段a上的出行时间依然可以用BPR路阻更新函数来计算，即

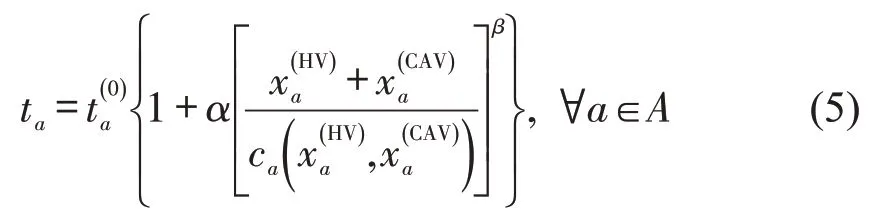
式中：为路段a上的自由流时间；为新型混合交通流下路段a的通行能力，由式（1）计算得到；α和β是BPR函数中的参数。

同样地，定义εHVE为路段上单位CAV 流量等价为HV 流量（即标准交通量）的折算系数，根据路段行驶过程中CAV 对道路空间的占用，该折算系数可以计算为

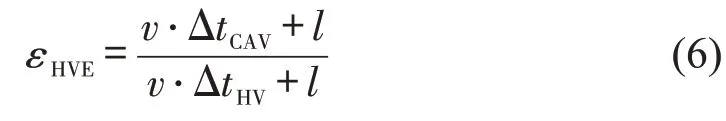
式中：v为路段上车辆的行驶速度。

基于定义的εHVE，可以将路段上的混合交通流量转化为等价的纯HV 流量[9]。相应地，在BPR 路阻更新函数中，路段通行能力可采用只有HV存在时的路段通行能力ua，因此，混合交通流在路段a上的出行时间也可计算为

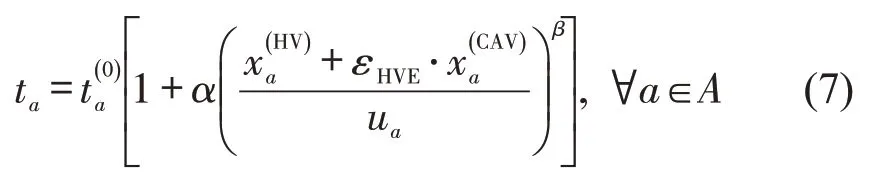
（2）路径出行时间

设R和S分别为路网上起点集合和终点集合；r和s分别表示某个起点和终点，r∈R，s∈S；和分别表示OD 对rs间的HV 路径集和CAV路径集。车辆路径出行时间由该路径包含的所有路段出行时间和节点出行时间组成，其计算式为

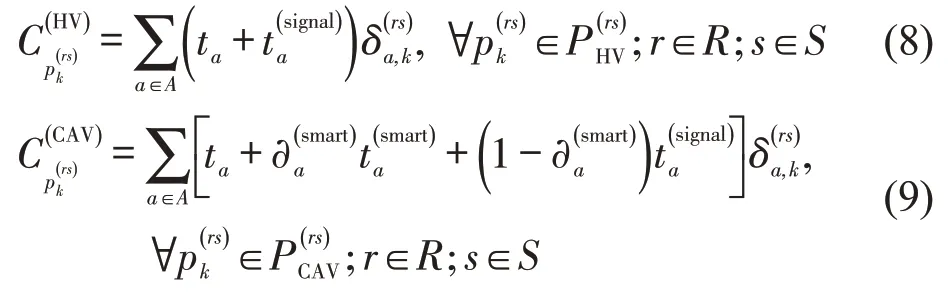
式中：为OD 对rs之间的第k条路径；、分别为HV、CAV 在路径上的出行时间；为0-1 变量，若路段a下游交叉口是智能交叉口，为1，否则为0；为路段a与路径之间的关系，若路段a在路径上，为1，否则为0。

2.2 流量约束

（1）需求约束

起终点之间所有路径上某类车流量之和应该等于起终点对该类车辆的出行需求量，即

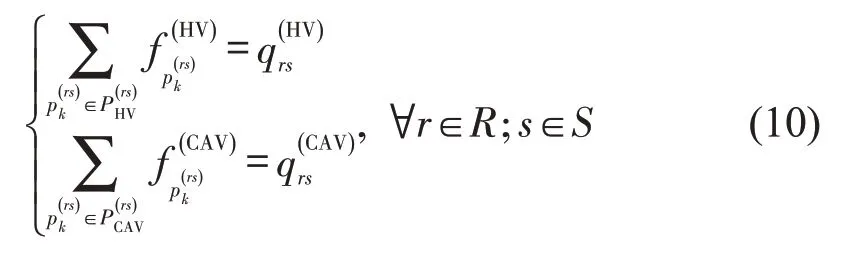
（2）非负约束

每条路径上的HV 流量和CAV 流量应该是非负的，即

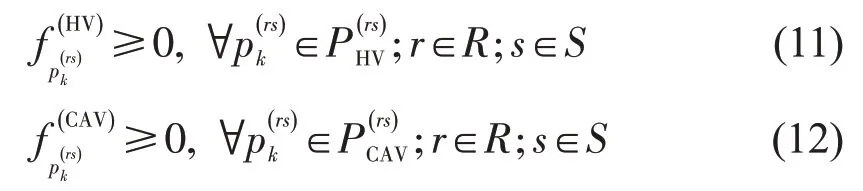
路段a上的车流量等于经过该路段的所有路径的车流量之和，即

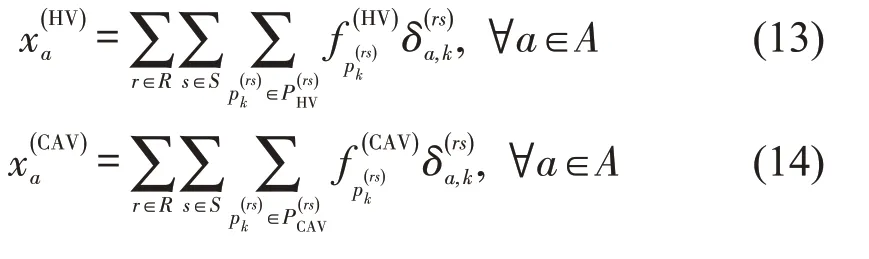
2.3 混合用户均衡模型

本文提出整合UE 和SUE 的混合用户均衡模型描述两类出行者的路径选择行为。

2.3.1 混合用户均衡条件

假设HV出行者和CAV出行者都是理性的，即都会选择最短路径出行。基于CAV 第二个特性，CAV 可以准确地感知到达目的地的最短路径，因此，假设其路径选择行为遵循用户均衡（UE）准则，当达到用户均衡时，所有被使用的路径阻抗都相等且等于最小阻抗，没有被使用的路径阻抗都大于等于最小阻抗，均衡状态下的CAV路径流满足

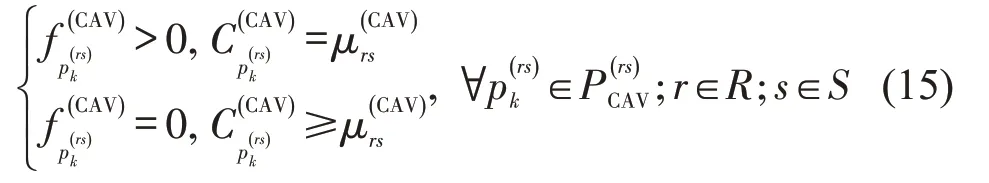
式中：为OD对rs之间CAV的最小路径阻抗。

而HV 出行者由于获取路网信息的能力有限，感知到的最短路径与实际的最短路径存在感知误差，其路径选择行为遵循随机用户均衡（SUE）原则，当达到随机用户均衡时，没有用户相信可以通过单方面改变路径减少出行成本，均衡时的HV路径流满足

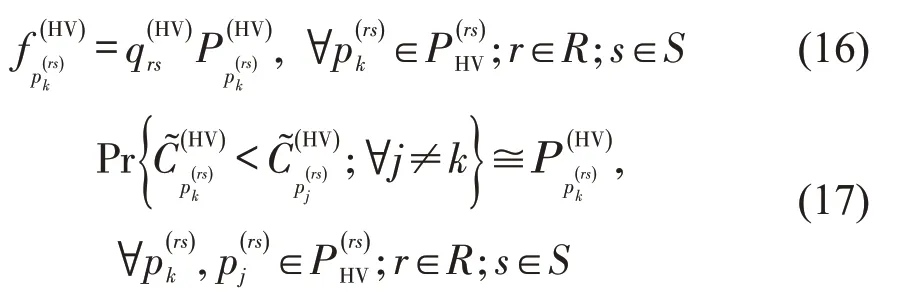
式中：为路径被HV出行者感知到为最短路径的概率，也是这条路径被用户选择的概率；分别是HV 出行者对路径、的感知出行阻抗，其中，为任意一条不为的HV路径。

由于感知能力有限，HV 出行者感知的路径出行成本与实际的路径出行成本之间总是存在随机感知误差ek，假设出行者对所有路径的感知误差项都服从Gumbel 分布，则所有路径的感知误差可以用e表示，其感知的路径出行阻抗可以表示为实际路径出行阻抗加上感知误差，即。采用基于Logit的随机用户均衡模型描述HV出行者的路径选择行为，则路径被HV出行者选择的概率为

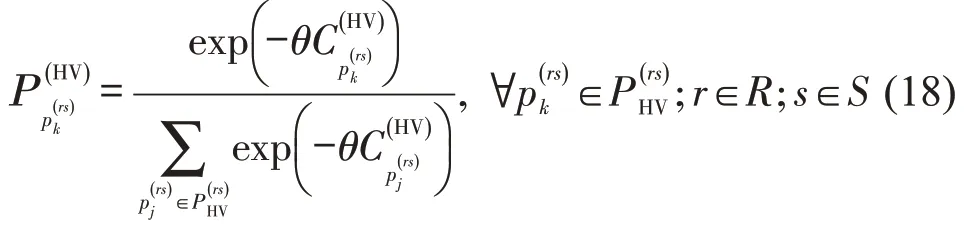
式中：θ为衡量出行者感知误差的参数。

2.3.2 混合互补问题建模

由式（3）～式（8）可知，出行成本函数是不可分离且不对称的，由于其复杂性，很难找到等效的数学规划模型描述该问题。因此，本文将新型混行模式下的混合用户均衡问题描述为一个变分不等式问题。

设κ是HV 可行路径流和CAV 可行路径流的集合，也是HV 路径流和CAV 路径流的可行解空间，其定义为

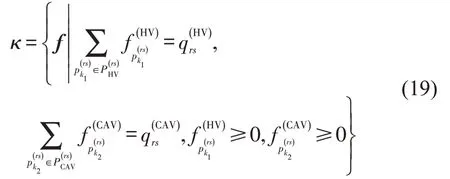
式中：f为路径流量的列向量，即

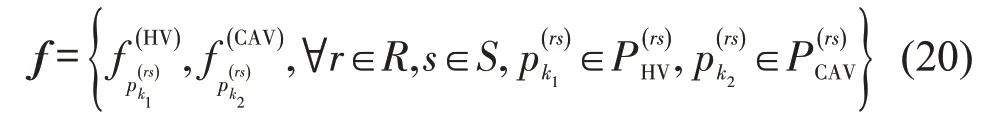
为方便表述，定义fHV和fCAV分别为HV 路径流和 CAV 路径流的列向量 ， 即为HV 路径出行成本的列向量，即C（fCAV）为CAV 路径出行成本列向量，即；μ为所有OD 对之间最短路径阻抗的列向量，即

面向新型混合交通流的混合用户均衡问题可以描述成如下变分不等式问题：给定可行路径流集合κ和一个映射关系Φ（fHV） ，其中，。变分不等式问题VI（Φ（fHV）,C（fCAV）,κ），可以表述为找到一个可行路径流满足

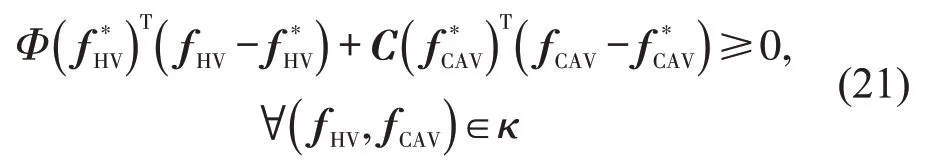
该变分不等式混合用户均衡条件的等价性，可以通过该变分不等式问题的一阶最优性条件与上述混合用户均衡条件证明，这里不再赘述。

为提高计算效率，进一步建立基于路径的非线性混合互补问题描述混合用户均衡问题。基于HARKER 等[10]提出的命题2.2 以及FACCHINEI等[11]提出的命题1.2.1，可以得到与变分不等式问题VI（Φ（fHV）,C（fCAV）,κ）等价的非线性混合互补问题，找到向量（f,μ）满足

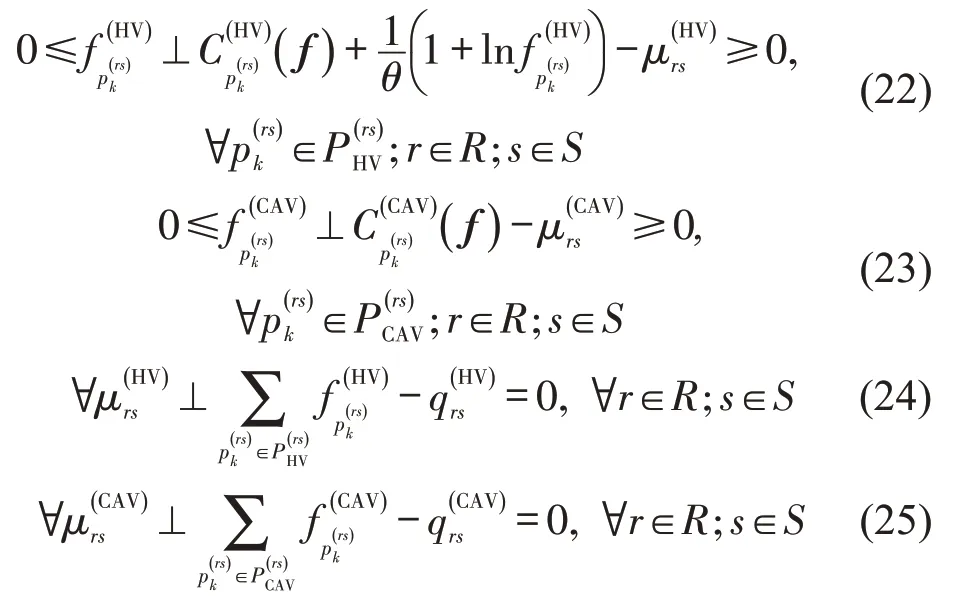
式（22）和式（23）表示混合用户均衡条件，式（24）和式（25）表示OD对之间的路径流满足需求约束。

3 智能交叉口网络布局优化问题

在新型混合交通流的城市路网中，交通规划者将面临决策哪些交叉口设为智能交叉口，哪些设为传统视觉交叉口，以使城市路网通行效率最大化的挑战。为此，本文建立了整合混合用户均衡的智能交叉口网络布局优化模型。

3.1 HV可达性约束

在路网上规划智能交叉口后，CAV的路网结构不会发生变化，但由于HV 无法通过智能交叉口，其路网结构相较原路网会发生显著变化，可能会出现某些OD 对之间HV 不可达的情况，如图4（b）所示。因此，为保证每一个方案下，HV在有出行需求的OD对之间可达，需要引入HV可达性约束条件。

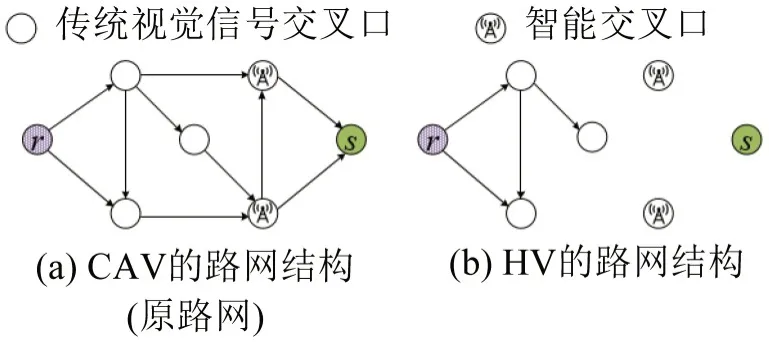
图4 智能交叉口网络布局方案下CAV与HV的路网结构对比Fig.4 Comparison of HV'network structure and CAV'network structure under planning smart intersections

ηi为0-1变量，ηi=1 表示交叉口i为智能交叉口；ηi=0 表示交叉口i为传统视觉信号交叉口。η为交叉口类型ηi组成的列向量，即η={ηi,∀i∈N}，由此可知，η表示智能交叉口网络布局方案。

令表示原路网的邻接矩阵，，其中，1 表示在路网中节点i与节点j相邻，否则，0。显然，在给定城市路网中，Γ（0）是外部给定且已知的。对于智能交叉口网络布局方案η对应的城市路网，令Γ表示对于HV而言路网的邻接矩阵，Γ={γij,∀i,j∈N}，其中，γij=1 表示节点i与节点j均为传统视觉信号交叉口且在原路网中相邻（即1），否则，γij=0。因此，智能交叉口网络布局方案η与HV邻接矩阵Γ需要满足

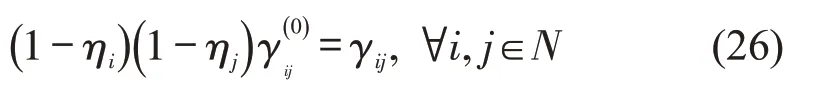
对于智能交叉口网络布局方案η对应的城市路网，采用可达矩阵B描述HV 在任意OD 对之间的可达性，B={bij,∀i,j∈N,i≠j} ，其中，bij=1 表示节点i与节点j之间HV可达；bij=0，则表示HV不可达。可达矩阵是典型的布尔矩阵，可由路网邻接矩阵的m次幂经过布尔相加得到，即

式中：（Γ）m为邻接矩阵Γ的m次幂，由于任意两节点之间最多经过n-1 个节点到达，所以，1 ≤m≤n。

对于HV 有出行需求的OD 对rs（即0），智能交叉口网络布局方案η应该保证HV在该OD对间的可达性（即brs=1）。因此，智能交叉口网络布局优化方案应满足

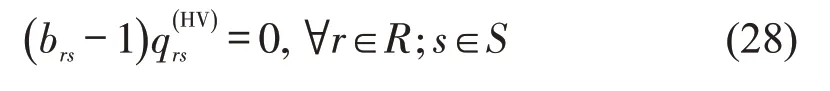
3.2 智能交叉口网络布局优化模型

选取两类出行者在路网上的总出行时间最小化为优化目标，建立智能交叉口网络布局优化模型。由于交通规划者决策过程中需要考虑均衡时出行者的路径选择[12]，因此，该优化问题决策变量为智能交叉口规划方案η、HV 路径流量fHV及CAV路径流量fCAV。关于约束条件，除了HV可达性约束以及可行路径流的约束，路径流f同时还应该满足混合用户均衡条件，由于式（15）和式（16）混合用户均衡条件与非线性互补问题的等价性，路径流应该满足非线性互补问题的互补松弛条件。综上所述，智能交叉口网络布局优化模型为

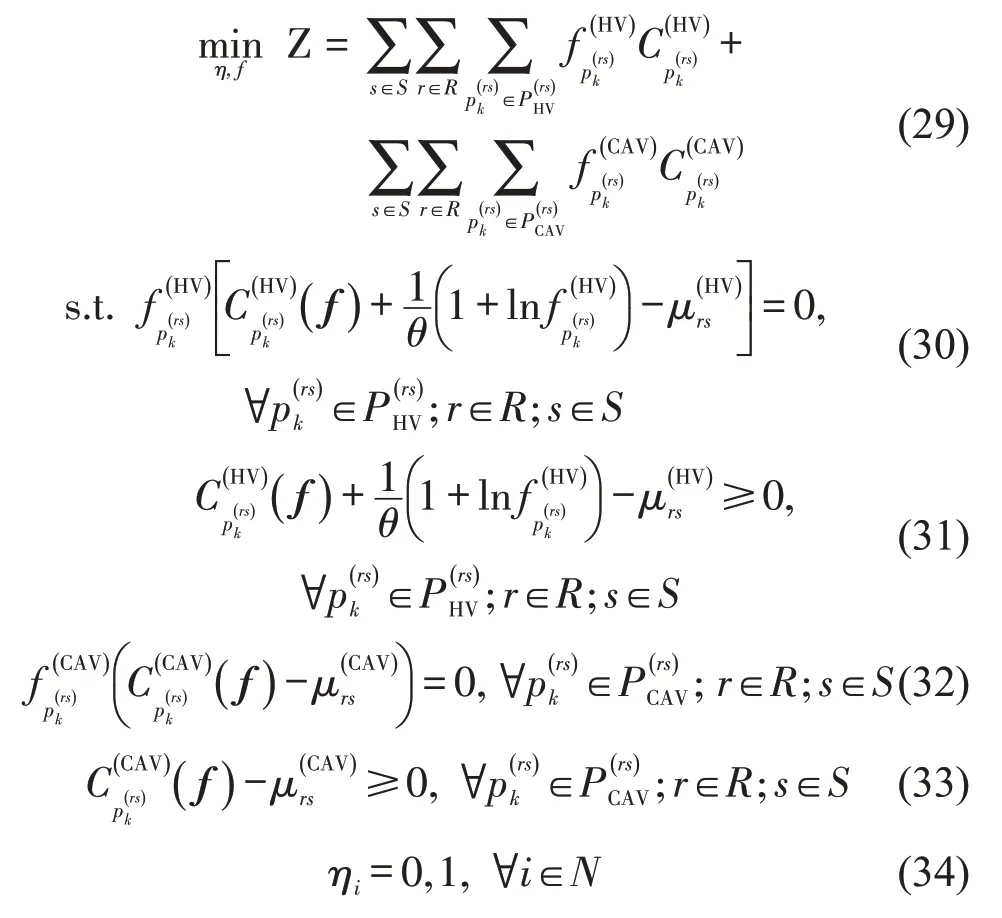
式中：Z为该规划模型的优化目标，即新型混行模式下的路网总出行时间；η、f为决策变量。

式（11）、式（12）及式（30）～式（33）为混合用户均衡约束；式（34）为ηi决策变量0-1约束。此外，需求约束为式（10），路段流量与路径流量的关系为式（13）和式（14），路径阻抗与路段阻抗的关系为式（8）和式（9），HV可达性约束为式（26）～式（28）。

4 求解算法

鉴于所建立的智能交叉口布局优化模型是一个混合整数非线性规划问题，同时，含有非线性混合互补约束条件及布尔运算，因此，采用改进的遗传算法求解。其中，为保证初始解满足可达性约束，提出了初始可行解启发式生成算法；针对遗传算法交叉变异过程中产生的不可行解，设计了不可行解修复算法；针对优化模型中描述混合用户均衡的非线性混合互补约束条件，利用GAMS 中的PATH求解器寻找满足该约束的流量分布。

4.1 初始可行解启发式生成算法

随机生成满足约束式（34）的初始解η，HV 可达性约束式（26）～式（28）可能不会被满足，同时，由于可达矩阵需要通过布尔运算得到，无法直接随机生成同时满足所有约束的初始可行解。为此，本文设计了一个启发式算法保证生成的初始解满足HV可达性约束。

算法具体步骤如下：

Step 1 生成所有OD对之间的有效路径存放于集合K。

Step 2 在HV 出行需求大于0 的每个OD 对rs之间按照以下步骤选择1 条HV 路径（HV 路径）保证HV 可达，即对于路径上的任意节点p都规划为传统视觉信号交叉口，即ηp=0。

Step 2.1 初始化。I为未选HV 路径的OD 对集合，为集合I中的第i个OD 对，令i=1；J为已选HV 路径的OD 对集合，令J=∅，r（j）s（j）为集合J中的第j个OD对；Psign为集合J中所有OD 对间的HV 路径覆盖的节点集合。

Step 2.2 计算出OD 对r（i）s（i）间所有路径覆盖的节点数，以及集合J中的所有OD 对间的HV 路径覆盖的节点数Step 2.3 计算OD 对间每条路径与所有已选 HV 路径覆盖的总节点数按由小到大的顺序排列r（i）s（i）间的所有路径。

Step 2.6 如果I=∅，返回Step 3；否则，i=i+1，返回Step 2.2。

Step 3 对于所有HV路径覆盖的节点p∈Psign，使ηp=0。

Step 4 随机生成路网上剩余节点q∈N且q∉Psign对应的决策变量值，ηq=0 或1。

4.2 不可行解修复算法

在使用遗传算法求解智能交叉口规划问题时，遗传和变异过程中可能会生成不满足HV 可达性的解，本文设计启发式算法修复生成的不可行解，具体步骤如下：

Step 1 输入不可行解Ochild，计算Ochild方案下有HV 出行需求的每个OD 对之间的最短路出行时间，存放至集合QTime中，

Step 2 寻找QTime中最短路出行时间为inf（即HV 不可达）的OD 对集合

Step 3 将ηi=1 的节点i所连接路段的出行时间ta由inf改为一个很大的数M，求集合U中第一个OD 对ru1su1之间的最短路径，对于路径上的任意节点i，令ηi=0 ，得到修复后的解Ochild。

Step 4 计算Ochild方案下有HV 出行需求的每个OD 对之间的最短路出行时间，存放至集合QTime中，

Step 5 如果QTime中值为inf的元素个数为0，则输出可行解Ochild′=Ochild；否则，返回Step 2。

5 案例分析

本文选取经典的Sioux-Falls 网络进行案例分析，如图5 所示，该网络包含24 个节点，76 个路段和4 个OD 对，分别为1～15，3～19，6～24 及13～8，图中数字为节点及路段编号。路段的自由流时间、自由流速度及基础通行能力等路网基本属性数据均来源于Github 网站，BPR 函数中的参数取α=0.15，β=4 。HV 驾驶员和CAV 的反应时间分别为1.5 s 和0.6 s。传统视觉信号交叉口的信号周期时长为120 s，交叉口宽度为24 m[6]，CAV 在交叉口内部的平均车速为20 km·h-1，平均车身长度为4 m。

求解算法中的参数设置如下：交叉概率0.9，变异概率为0.15，种群规模为20，最大进化代数为200代，随机路径选择概率参数σ取0.05。

5.1 结果分析

HV 和CAV 的OD 需求分布如表1 所示，城市交通系统中CAV占比设为50%。

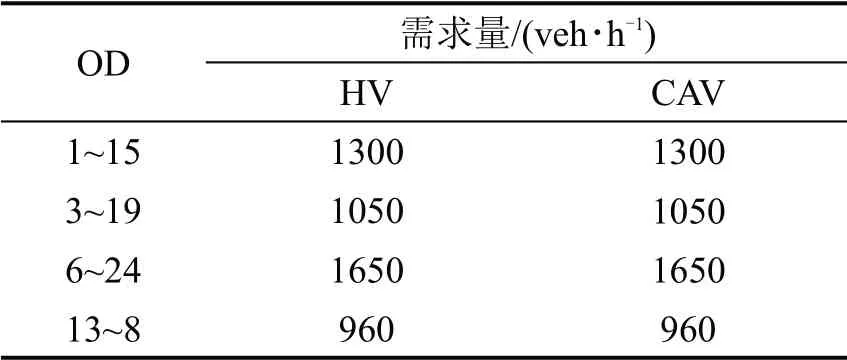
表1 OD需求分布Table 1 OD demand distribution

如表2所示，优化后的城市路网智能交叉口布局方案使路网总出行时间降低了10.78%，其中，HV总出行时间降低了15.64%，CAV 总出行时间降低了4.48%。智能交叉口在城市路网上的规划布局，同时降低了两类车辆出行者的出行时间，表明本文所提出的模型和算法具有很好的优化效果和可行性；同时，与CAV相比，HV出行效率得到更加显著的提高。这是由于优化后CAV 的路网结构不变，HV的路网结构变化较大，出行路径变化也较大，此外，在路网上规划了智能交叉口之后，一定程度上实现了HV与CAV在空间上的分流，且优化前CAV的总出行时间已经较小，所以，该布局优化方案较大幅度的优化了HV的出行时间。

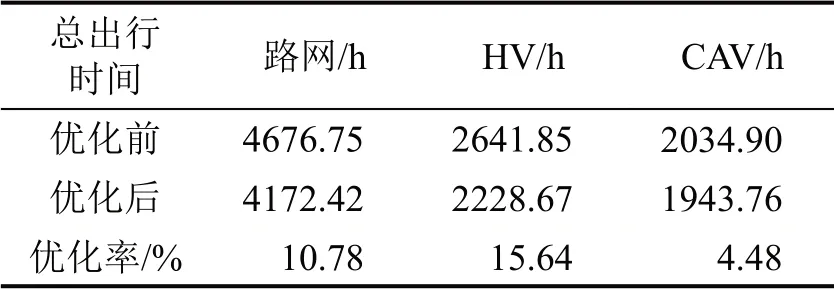
表2 路网总出行时间优化前、后对比Table 2 Total travel time before and after optimization

研究发现，优化前、后CAV 都有比HV 更小的总出行时间，这得益于CAV 更强的路网信息感知能力，出行路径为最短路，且与传统视觉信号交叉口相比，智能交叉口有较高的通行效率。此外，智能交叉口的规划布局在大幅改善城市交通系统整体出行效率的同时，也大幅降低了由于单方面技术优势所带来的CAV与HV的出行效率差距，增进了出行公平性。最优交叉口网络布局方案如图5 所示。交叉口网络布局优化迭代曲线如图6所示。

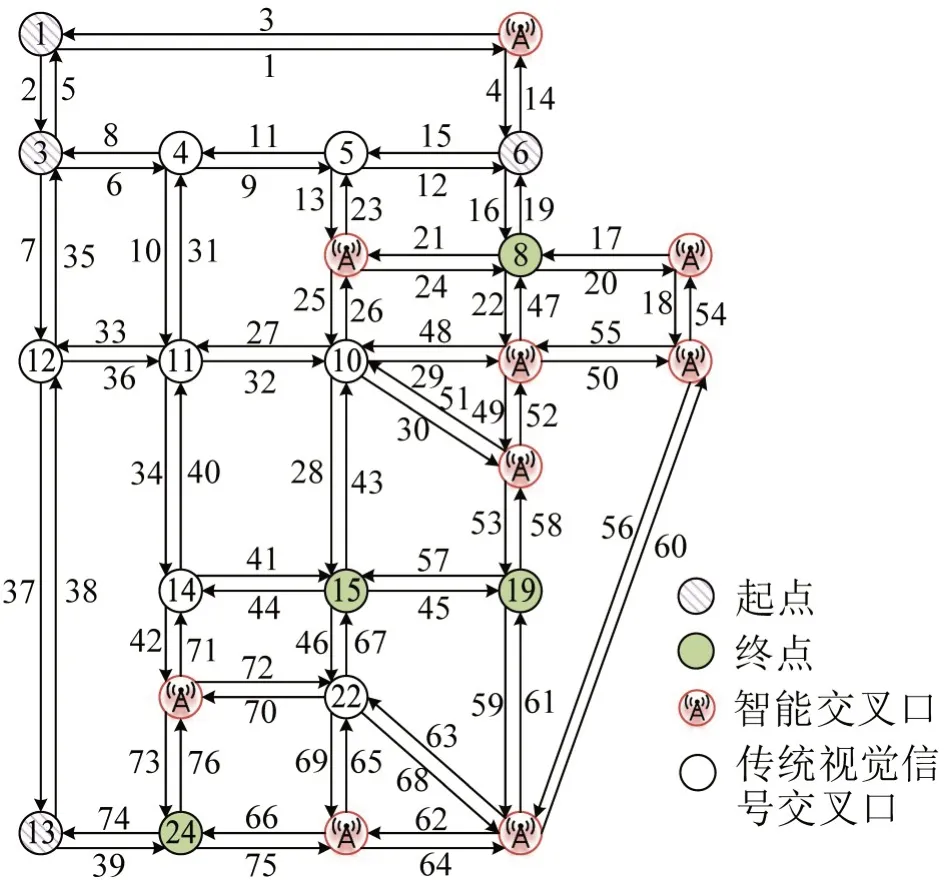
图5 最优交叉口网络布局方案Fig.5 Optimal intersection spatial layout scheme

由图5 优化后城市路网中智能交叉口的空间分布可知，最优的交叉口网络布局方案中有9个智能交叉口。优化结果表明，保证每个OD 对间HV可达性的前提下，为最小化路网总出行成本，交叉口会尽可能多的被设置为智能交叉口。由图6 路网总出行时间和优化过程中智能交叉口数量随迭代次数的变化曲线可知，随着迭代次数的增加，路网总出行时间不断减小的同时，路网中智能交叉口的数量呈现不断增多的趋势，同时，求解算法具有较好的迭代收敛性。

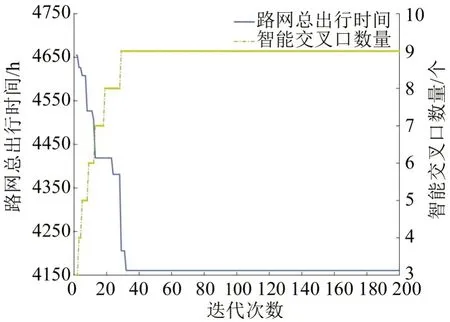
图6 交叉口网络布局优化迭代曲线Fig.6 Iteration curve of intersection layout optimization

5.2 灵敏度分析

网联自动驾驶技术的进步与日趋成熟，将会使越来越多的出行者选择CAV 出行，未来CAV 的市场渗透率将不断提高。本文在固定出行需求的条件下研究CAV渗透率变化对优化结果的影响。

保持城市路网中OD 出行需求分布不变，设置CAV 所占比例由10%～90%不断递增，不同占比条件下智能交叉口网络布局的详细优化结果如表3所示。

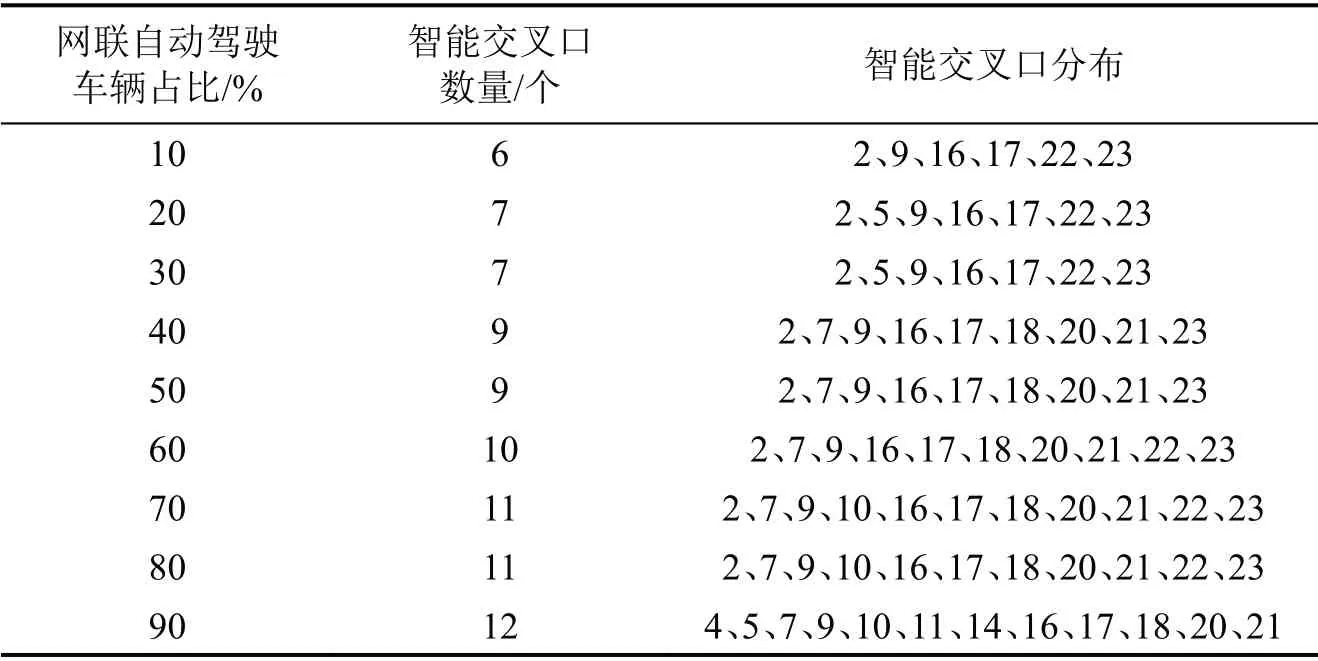
表3 CAV不同占比下智能交叉口优化的数量和分布Table 3 Number and distribution of smart intersections with different proportions of CAV

优化前、后路网总出行时间和总出行时间优化率随CAV 占比的变化曲线如图7 所示。由图7 可知，随着CAV占比不断增大，原路网和优化后的路网整体出行时间都在逐渐下降，进一步体现了CAV拥有较短反应时间以及精确选择最短路径的优势，此外随着CAV比例的增大，智能交叉口数量增加，交叉口总阻抗减小，进一步增大了道路通行能力，使路网整体出行时间减小。

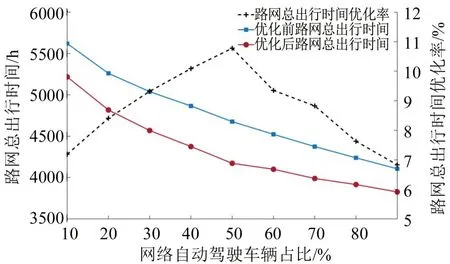
图7 CAV不同占比下的优化结果Fig.7 Optimization results under different proportions of CAV

由图7优化率曲线可知，本案例中路网总出行时间的优化率随CAV占比的增大呈现先增后减的趋势。CAV 占比较小时，为保证HV 在OD 对间可达，优化后的路网上智能交叉口数量较少，总出行时间的优化率也较小，随着CAV 占比的增大，如表3 所示，智能交叉口数量增多，优化率也随之增大，占比50%时，优化效果最好；CAV占比继续增大时，优化前的路网总出行时间较小，由规划智能交叉口带来的边际效益递减，总出行时间优化率下降。CAV占比90%时，优化后智能交叉口的空间分布如图8所示。

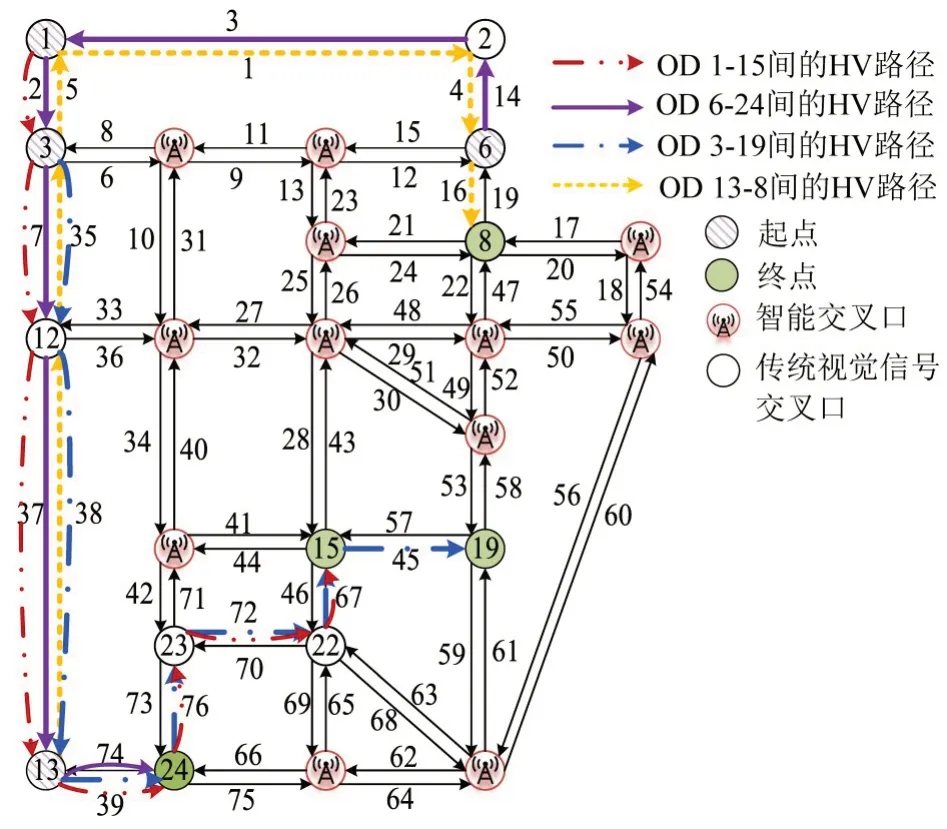
图8 CAV占比90%时优化后智能交叉口的空间分布Fig.8 Spatial Distribution of Smart intersections when CAV Account for 90%

如表3 所示，路网中CAV 占比越大，优化后的路网上智能交叉口的数量越多，特别是当CAV占比90%时，最优方案中共有12 个智能交叉口。由于HV 的数量较少，只占总需求量的10%，所以，在保证每个OD对间有1条HV出行路径后，路网上剩余交叉口全部被优化为智能交叉口，使得CAV 占比90%的情况下，路网上车辆总出行时间最小，表明优化模型和算法可以合理有效布局智能交叉口，降低路网总出行成本。

6 结论

针对CAV与HV混合行驶的城市交通系统，提出将部分交叉口改建为智能交叉口，以充分发挥CAV的技术优势，提高交叉口通行效率，同时，保留部分传统视觉信号交叉口，确保HV 在OD 之间的可达性。通过考虑CAV 与HV 的不同路径选择行为以及系统最优目标，在城市路网上合理地规划布局智能交叉口，主要得出以下结论：

（1）CAV 渗透率为50%的情况下，优化后的总出行时间可减少10.78%，表明在混行路网上合理布局智能交叉口，使路网总出行时间显著下降；此外，研究发现，智能交叉口的修建对路网中HV 的出行时间优化较大，大幅降低了由于单方面技术优势所带来的CAV与HV的出行效率差距，增进了出行公平性。

（2）CAV 渗透率越大，优化后路网上的智能交叉口数量越多，优化方案保证HV可达的前提下充分发挥了CAV的技术优势；此外，随着CAV渗透率增大，由于智能交叉口数量变化和边际效益递减等原因，路网总出行时间优化率呈现先增大后减小的趋势。