基于三角网格曲面的机器人磨削工具姿态光顺优化＊

金 鑫 刘其广 吕 杰 徐飞飞 孙晓楠

（①中国航发北京航空材料研究院，北京 100095；②北京市先进运载系统结构透明件工程技术研究中心，北京 100095）

三角网格曲面由于拓扑结构简单和计算效率高等优点[1]，在汽车、船舶和模具等领域得到广泛应用。尤其随着数控加工领域针对网格曲面刀位轨迹生成方法研究的深入[2-7]，针对基于三角网格曲面表示的工件磨削、平整需求也日益增多。然而，作为分片线性曲面，三角网格曲面缺少连续的法矢及曲率等局部微分几何信息；加之网格曲面作为真实模型的逼近曲面，存在精度损失的问题。因此，为了保证磨削过程的平稳性和磨削质量的均匀性，在利用机器人对三角网格曲面表示的工件进行磨削处理时，如何综合考虑网格曲面的局部微分特性，设计出相应的磨削工具姿态光顺优化算法，从而产生光顺性良好和过渡均匀的磨削工具姿态，成为目前亟需解决的问题。

在数控加工中，为解决三角网格曲面缺少连续的法矢及曲率的问题，不少研究学者给出了相对成熟的解决方案。在计算三角网格节点处的单位法矢时，常见的做法是对该节点周围的三角面片的法矢做面积加权平均[1,3]，或考虑周围的三角面片形状等因素采用角度正弦加权等加权方式予以改进[4,8]。另外，为了对曲面凹凸性判别及加工工具姿态进行合理规划，需要对节点处的曲率信息进行合理估计。相较于采用Taubin方法[9]、基于多截形法的曲率估计[3]即Voronoi方法[10]等策略，本文中采用对局部顶点进行精确的参数曲面拟合的方式来进行曲率估计[4]，该方式在操作和可控性上显得更为灵活，能够更好地为基于网格曲面的机器人磨削工具姿态光顺优化算法提供必要的曲面信息的支持。

另一方面，数控加工中在对加工工具姿态进行优化时，通常采用基于启发式算法[11]、最短路径算法[12]、样条拟合[13]或径向基函数插值[14]的方式来实现加工工具姿态间的平稳过渡。同样的，在使用机器人对网格曲面的工件进行磨削、平整的过程中，也需要对磨削工具的姿态变化的光顺性进行优化，从而避免磨削工具姿态变化剧烈导致的磨削表面的不均匀及机器人关节电机负荷过大。考虑到四元数插值在姿态过渡上的优势[15]：能产生角速度均匀的姿态过渡、计算效率高及算法逻辑清晰，本文以四元数插值作为机器人磨削工具姿态光顺优化策略，实现对三角网格曲面磨削工具的姿态规划。

具体而言，本文将首先对网格曲面的法矢、曲率等局部微分几何信息进行计算，并基于所获得的的法矢和曲率信息，指定关键路径点的磨削工具姿态，最后通过四元数插值的方式对磨削工具姿态进行光顺，从而实现对磨削过程中机器人末端运动的优化。

1 三角网格曲面的微分几何特性

1.1 法矢和曲率估计

曲面的法矢是加工过程中工具姿态调整的重要参考，然而三角网格曲面作为分片线性曲面，在节点处缺少连续的法矢和曲率信息。因此，对网格曲面的机器人磨削工具姿态光顺性优化而言，首先需要对网格曲面的节点处的法矢进行估算。

如图1所示，在三角网格下标为i的节点 υi处，所对应的法矢ei可以由该节点星形邻域附近的面片的法矢做面积加权平均得到，记该节点附近的三角面片的面积和法矢分别为si,j、ei,j，j=1,2,···,m，具体公式如下。

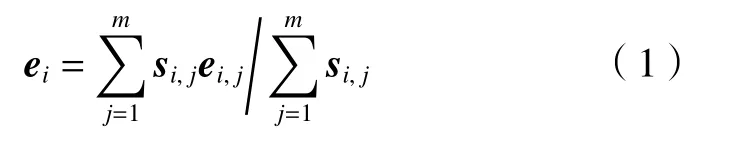
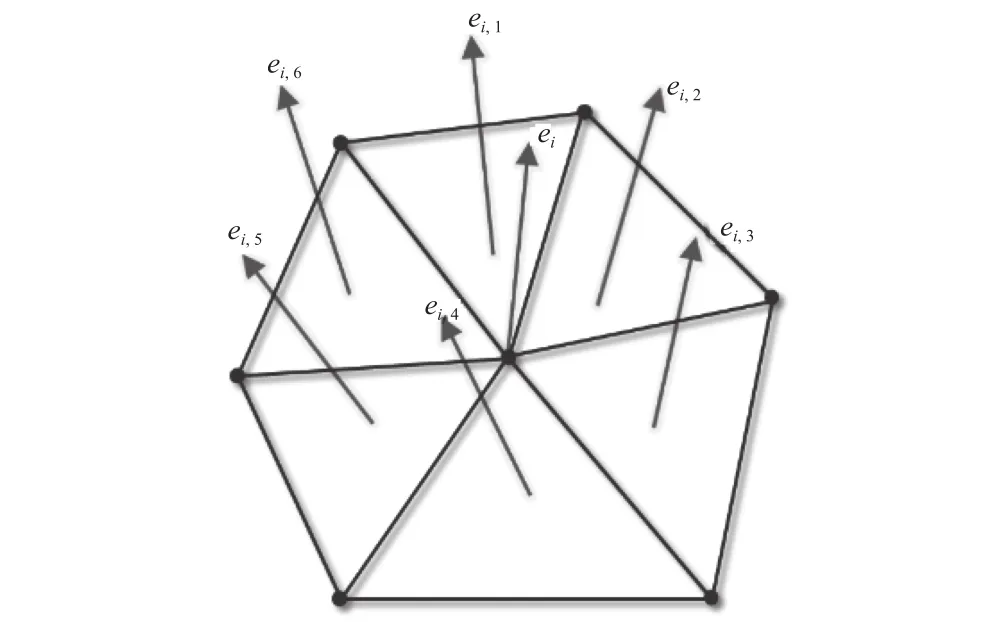
图1 网格曲面节点的星形邻域

除了法矢之外，三角网格曲面的曲率信息仍待估算。曲率反映了曲面或曲线在该点的弯曲程度，是姿态规划算法的重要依据。

对三角网格曲面的曲率估计，对计算效率要求较高，同时要求其估算的适应能力好，即能够依据精度的要求进行灵活调整。本文采用三次 B e’zier曲面进行对三角网格曲面的节点进行局部拟合，根据拟合曲面计算相应点的曲率。三次 B e’zier 曲面的表达式

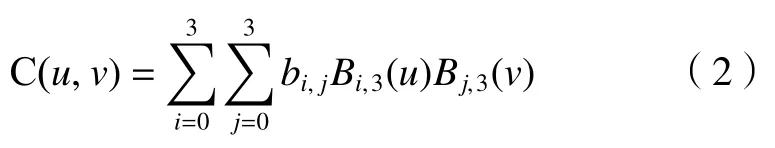
其中：bi,j为 B e′zier 曲面的控制顶点，u、v为曲面的参数，bi,3(u)、Bj,3(v)为Bernstein基函数。

为完成三次 B e′zier 曲面的拟合过程，需要对 υi邻域的节点Qj(xj,yj,zj)进行参数化，然后利用最小二乘法求取拟合曲面。本文对节点进行参数化的过程如下。

（1） 计算点集Qj的最小二乘平面

记最小二乘平面的方程为

利用式（4）在极值条件下，计算得到相应的系数和最小二乘平面方程。

（2）将节点Qj投影至最小二乘平面上。

（3） 将所得投影点缩放至 [0 ,1]×[0,1]的矩形域中，获得Qj对应的参数值

然后，将节点Qj及对应的参数值代入式（2）中，获得线性方程组AX=B，求解该方程，完成拟合过程。

接着，根据局部拟合得到的 B e′zier曲面方程，若经过节点 υi的磨削路径曲线为r(u(t),v(t))，依据式（5）计算节点 υi处的曲率：

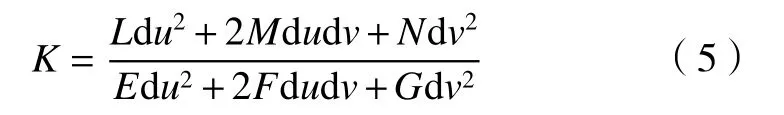
其中：K为曲面在该点处的法曲率，E、F、G为曲面第一类基本量，L、M、N为曲面第二类基本量。

1.2 关键路径点的姿态指定

利用等参数法，按步长 Δt，将磨削路径曲线r(u(t),v(t))分割成离散 的 路 径点rk(k=1,2,···,m)。 随后利用1.1节中介绍的法矢和曲率估计方法计算每个 离 散 路 径 点 处 的 法 矢ek(k=1,2,···,m)和 曲 率Kk(k=1,2,···,m)。基于离散点处的曲率信息，按照以下流程指定关键路径点，并对关键路径点进行姿态指定：

（1）计算曲率序列Kk(k=1,2,···,m)的平均值。

（3）遍历曲率序列，{将曲率值大于曲率阈值Kc的}路径点区域视作关键区域rk1,rk2,···,rks,···,rki1,rki2,···,rkit，并将每个关键区域内曲率值局部最大的路径点视作关键路径点。

（4）将关键路径点的姿态指定为该点处的法矢。

至此，完成了关键路径点的机器人磨削工具姿态的指定，为后续机器人磨削工具姿态的光顺性优化做好了准备。

2 四元数插值和姿态优化

本文采用四元数插值算法对机器人磨削工具姿态的光顺性进行优化，从而获得光顺性良好和过渡均匀的磨削工具姿态。下面介绍四元数插值的具体流程。

四元数是一种[具有4个]分量的、形如q=q1i+q2j+q3k+q4=q1,q2,q3,q4的超复数[16]，其中i,j,k为虚轴单位，满足i2=j2=k2=-1，ij=-ji=k，jk=-kj=i，ik=-ki=-j。

对于三维空间中的某一单位矢量en=[en,i,en,j,en,k][，(在四元数)空间]内可以被表示为一个纯四元数En=en,i,en,j,en,k，0。若指定某一固定单位矢量eref作为参考矢量，则由参考矢量eref到单位矢量en的旋转变换可以被表示为

其中：Eref为参考矢量eref所对应的纯四元数；是qn的共轭四元数，qn为由eref到en所经旋转变换对应的四元数，且该四元数qn的计算公式为

下面利用四元数插值，对章节1中所指定的关键 路 径点序列rn(n=1,2,···,N)所对应的 姿 态 序列（即该点的法矢）en(n=1,2,···,N)进行插值，生成中间矢量作为过渡磨削工具姿态。具体做法如下：

（1） 选取参考矢量eref，并按照式（7）计算eref旋转至姿态序列中每一个姿态en(n=1,2,···,N)所对应的四元数qn(n=1,2,···,N)。

（2）在所获得的四元数序列中，顺序选取两相邻四元数qn,qn+1(n=1,2,···,N-1)，按照式（9）进行四元数插值，得

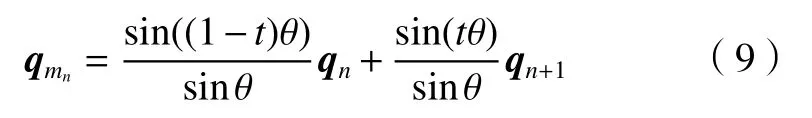
式中：mn=1,2,···,Mn;t∈ [0,1]。Mn为两关键路径点rn和rn+1中间待插值的路径点数目，参数 [0 ,1]可将区间 [0 ,1]经Mn等分得到。

（3）在获得所有路径点的姿态所对应的四元数后，需要将其转化为该点的姿态。具体做法是，在每个路径点处，按照插值得到的四元数qmn，利用式（7）对参考矢量eref做旋转变换，得到所有中间路径点的姿态emn。

按照上述流程优化后的磨削工具姿态，如图2所示，可以看到生成的中间磨削工具姿态具有很好的均匀性。

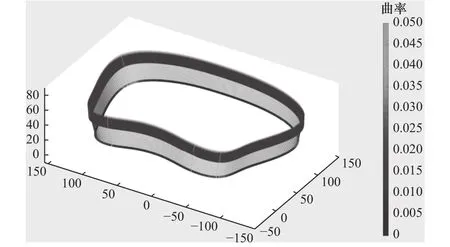
图2 四元数插值产生的磨削工具姿态

3 实例验证

图3所示为MATLAB实现磨削姿态规划算法的可视化仿真环境，以及所使用的三角网格曲面。

图3 算法的MATLAB界面及三角网格曲面

下面通过与未进行优化的磨削姿态进行对比，以验证本文算法的优越性。注意：未进行优化的磨削姿态指的是，将路径点处的法矢直接作为磨削工具姿态。基于上述算法流程展开仿真，仿真结果如图4所示。

图4 仿真实例

图5为实验结果，通过对优化前后的磨削工具姿态运动学表现进行对比，以验证运动光顺性是否得到提高。其中，磨削工具姿态运动学表现为：整个运动过程中磨削工具姿态的角速度。

图5 加工实验

利用向前差分，得到角速度的离散表达形式

式中： ω为角速度；f为加工过程中的进给率； φi为参数为ti时磨削工具姿态相对于绝对坐标系z轴的转角；Li为时间ti至ti+1内磨削工具末端点移动距离。

图6所示为优化之前与优化之后的角速度曲线。可以看出，角速度的波动与优化之前相比明显降低。

图6 磨削工具姿态的角速度

4 结语

本文针对网格曲面磨削过程中遇到的问题，提出了相应的磨削姿态规划，所提出的具体算法具有以下特点：以局部拟合的方式对三角网格曲面进行法矢和曲率估计，并基于所获得的法矢和曲率信息，进行了关键路径点及其姿态的指定。然后，通过对磨削过程中机器人磨削工具姿态进行四元数插值，获得了更好的磨削工具姿态变化的均匀性，从而得到了更好的磨削工具姿态过渡的平稳性。经实例验证，本文所提算法优化后的磨削过程中，磨削工具姿态的角速度差起伏程度下降，波动减少，平稳性提高；同时，曲面的磨削效果更加均匀。