基于可视图谱信号特征提取的滚动轴承故障诊断＊

周建民 黄熙亮 熊文豪 王云庆 夏晓枫

（①华东交通大学载运工具与装备教育部重点实验室，江西 南昌 330013；②轨道交通基础设施性能监测与保障国家重点实验室，江西 南昌 330013）

滚动轴承作为工业设备中核心部件，倘若在运行中出现故障，将会带来难以估计的损失[1-2]。故对其故障诊断必不可少。其中对轴承振动信号特征提取是故障诊断的核心步骤[3]。近年来，有关滚动轴承传统的故障特征提取方法从时域、频域和时频域等中提取相关特征指标[4]。但由于滚动轴承的故障信号存在非平稳性，在时域、频域中难以提取简单有效的故障表征特征[5-6]。因此，针对滚动轴承故障特征提取方法还需不断加深研究。

近年来随着图信号不断快速发展，传统信号处理方法开始扩展图信号处理，使得图信号处理[7]（graph signal processing，GSP）成为信号分析处理中重要的分支。目前，图信号处理方法已经广泛应用于气候变化及图像处理等领域[8-9]，然而该方法在滚动轴承故障诊断领域应用较少。

相较于传统振动信号处理方法，图信号方法是研究振动信号关系的图结构。复杂网络是一种特殊的图结构，对于非平稳性信号，能够很好地捕获特征。可视图算法（visibility graph, VG）[10-13]是一种能将时间离散序列转变成复杂网络的算法。由于机械振动信号也属于一维时间序列，因此将振动信号转换成可视图复杂网络。近年来，已有部分学者开始初步进行研究。高艺源等[14]将图谱指标直接应用在滚动轴承故障特征提取中，将振动一维信号转换成图的形式，与传统时域和频域方法对比，体现出该方法的优越性。陈芒等[15]通过改进图结构数据，提出了可视图图谱幅值熵的概念，将振动信号转换成可视图信号，并由此计算得到故障特征参数，最后采用马氏距离识别滚动轴承故障类型。

将图信号处理方法应用于滚动轴承故障诊断领域，提出一种可视图图谱信号特征提取的故障诊断方法。通过将滚动轴承振动信号转变可视图信号，计算邻接矩阵和拉普拉斯矩阵的特征值与特征向量，得到相应的图谱指标，结合支持向量机分类算法实现滚动轴承故障诊断分类。通过实验验证分析，与传统的故障特征提取方法相比，能有效对不同类型的滚动轴承进行识别，更能有效地区分不同程度外圈故障，突出该方法的优势。

1 故障特征提取和分类

1.1 可视图的特征提取

为了充分获取轴承振动信号的故障信息，需要将一维离散时间序列转化成图结构数据。图主要由节点及节点间的连边组成，而邻接矩阵可以表示图中节点与节点之间关系的度量，是一个二维数组存放顶点间关系的矩阵。其图结构如图1所示。图中横坐标n1-n5为振动数据序列号，纵坐标表示每个时间节点的信号值大小xi。虚线表示图数据中的2个顶点有边连接，边的距离加权方法可参考欧式距离式（1）。

式中：邻接矩阵w分别是由节点vi值 与节点vj值通过欧式距离公式得到，这种欧式距离计算所得出的邻接矩阵弥补了等权加值的缺陷，可以描述节点vi与节点vj之间的差异性，并且节点之间差异性的大小可以通过欧式距离来定量体现，更加客观地表示出轴承采样信号的差异性。

可视图数据的构建是基于路图构建思想[7]而来，其可视图的可视性可参考式（2）。

式中：取两个相邻顶点 (n1,x1)与 (n2,x2)，那么对于下一个顶点 (n3,x3)，其中n1＜n2＜n3，通过可视图准则可以发现，若顶点 (n3,x3)与顶点 (n1,x1)计算得到的斜率大于顶点 (n2,x2)与顶点 (n1,x1)计算得到的斜率，则顶点(n3,x3)与顶点(n1,x1)可视。通过可视图的可视准则计算后，可将可视图信号图谱化，如图2所示，将图1的可视图信号相应可视图谱化。通常的路图只考虑了相邻两个点之间的联系，如图3所示，而可视图[15]既保持了原有的路图结构形式，且从图2中可以看出，同时又考虑了顶点与其他顶点的关联，扩大了其视野范围，相比于通常的路图形式，可以揭示出振动信号中更多的隐藏信息。

图1 可视图信号

图2 可视图图谱

图3 路图

将采集的轴承振动信号通过可视图构建后，计算各训练样本的邻接矩阵和拉普拉斯矩阵的特征值与特征向量，并基于此计算相应的图谱指标，具体公式见表1所示，表中 λi与μi分别为邻接矩阵特征值和拉普拉斯矩阵特征值。最后，计算每个训练样本的9个图谱指标组成特征向量空间，作为滚动轴承的初始特征指标。

表1 可视图图谱指标

1.2 特征选择

为更好地比较出各个特征指标的优劣，本文采用双样本Z值[16]来评估样本特征之间的差异。当特征值的Z值越大时，就能表明区分样本的能力越强，选择其区分能力强作为轴承优选特征。双样本Z值定义如下。

式中：i、j分别表示第i类和第j类；p表示第p个故障特征；Xi和Xj分别表示第i类的第p个特征值集合和第j类的第p个特征值集合；、和、分别为上述特征值集合的标准差和均值；ni和nj为对应的样本数量。

1.3 支持向量机分类

支持向量机（support vector machine，SVM）可以用于解决模式识别中的二分类及多分类问题。SVM算法的具体步骤如下所示。

首先，假设只考虑两类故障样本特征集合

式中：xi代表故障特征向量，有n维；yi代表标签类别，共有两类。在这两类样本中，可以通过核函数形成超平面，这里以线性核函数为例，得到的分类超平面为式（5），由式（5）可以计算点x到超平面的距离，如公式（6）所示。

因此，对于最优超平面问题可以用拉格朗日乘数法可以解决，对于不能用线性超平面分类的数据，可以利用非线性核函数将其映射到高维特征空间，从而建立最优分类超平面。此时，通过拉格朗日乘法将最优问题变成

约束条件为

式中：K(xi,xj)是将训练样本映射到高维特征空间中的核函数，在转换高维空间后得到最优分类超平面结果如下

式（9）表示通过核函数K(xi,x)将训练样本映射到高维特征空间；式（10）表示在高维空间后建立的最优超平面。因此，超平面分类问题可以表示成式（11）。

上述推导是通过SVM算法实现二分类问题，对于滚动轴承故障种类有多种，可以选择多个二分类SVM算法作为分类器，从而对滚动轴承的故障进行分类。

2 滚动轴承故障诊断流程

基于图谱指标特征提取的滚动轴承故障诊断流程如图4所示，具体可以分为以下几个步骤：

图4 故障诊断流程图

（1）将滚动轴承振动信号转换成可视图，分别计算每个训练样本的邻接矩阵和拉普拉斯矩阵，并得到相对应的特征值与特征向量。

（2）分别计算每个训练样本的图谱指标，通过双样本Z值选出前3个最大值，并由此选取对应的特征向量构成数据的故障特征向量。

（3）采用支持向量机算法，通过训练样本训练好超平面。

（4）在经过训练的 SVM模型中输入测试样本，从而实现滚动轴承的故障诊断分类。

3 可视图谱信号的滚动轴承故障诊断

3.1 滚动轴承不同类型的故障诊断

通过对滚动轴承的外圈、内圈和滚动体的特征提取，对所提出的方法进行了验证，采用美国（case western reserve university，CWRU）电气工程实验室的实验数据[17]，其提供球轴承实验的正常和有故障数据（包括轻度和重度故障，通过故障直径和深度来区分）。该实验台测试轴承型号为6205-2RS JEM SKF 深沟球轴承，轴承转速为 1 750 r/min，采样频率f=12 kHz，每次采样的长度N=2 048。电机轴承故障使用电火花加工来接种，轴承的内圈、外圈以及滚动体的故障直径为0.177 8 mm，深度为0.279 4 mm。

利用安装在滚动轴承驱动端基座上的加速度传感器来采集不同轴承在运行时产生的振动数据，对滚动轴承内圈故障、外圈故障、滚动体故障和正常轴承的振动数据采集，分别在其4种状态下取一个样本，其时域波形如图5所示。

图5 滚动轴承不同类型故障振动信号时域波形图

分别从上述4种状态下的数据各采集20个样本，每个样本长度为2 048，共有80个数据样本。将80个数据样本分成测试样本和训练样本两部分，训练样本取每种状态下的5个数据样本，测试样本取剩余的15个数据样本。准备好训练样本和测试样本后，其故障诊断流程如图4所示。首先，将20个样本数据全部进行0-1标准化，然后通过式（2）将振动数据转换成可视图结构数据，得到相应的可视图结构数据后，计算其邻接矩阵和拉普拉斯矩阵，再分别计算得到邻接矩阵特征值和拉普拉斯矩阵特征值。通过计算出的特征值得到表1的9个图谱指标，之后计算每类样本间的双样本Z值，选择双样本Z值前3个最大值作为故障特征输入向量，最后采用样本为 1～5、20～25、40～45、60～65序列号数据作为训练样本训练模型，其余数据作为测试样本。

将其滚动轴承振动信号转换成可视图之后的得到9个图谱指标，通过分别计算选取特征向量的双样本Z值，并将得到的双样本Z值大小通过折线图方式展示，如图6所示。

图6中，a～f分别表示4种状态下两两之间的双样本Z值。通过计算上述每种情况的双样本Z值分析可得：第一个特征指标与第8个和第9个特征指标区分能力相同，将以上6种情况对应的双样本Z值相加，计算得到前3个最大双样本Z值作为本次的故障特征向量输入。最后选择图能量指标、类拉普拉斯矩阵不变量指标以及图拉普拉斯能量指标作为本次的故障特征向量。对选取后的故障特征指标进行三维可视分析，得到图7。可以看出经过图谱特征提取后，内圈故障、滚动体故障、外圈故障和正常轴承的特征值有一个比较显著的区分，具有良好的聚集性，而且不同类型之间的故障基本上无重叠现象。总体上来看，通过该方法提取得到的特征展现出较高的类内相似度和较低的类间相似度，更有利于后期的滚动轴承模式识别。

图6 滚动轴承不同故障类型的双样本Z值

图7 各类轴承的图谱指标特征值

将处理好的训练样本数据作为SVM算法的特征向量输入，由于每一个特征向量大小差异很大，为了消除这种差距，对每一个输入特征采用0-1标准化来减少每一个输入特征之间的差异，将其输入到SVM算法模型中，训练得到最优超平面。将测试样本数据输入到已经训练好的SVM模型中，输出滚动轴承故障类别，最后将测试样本得到的类别与训练样本的已知的类别作为比较，分别如图8和9所示。

图8 训练样本

图9 测试样本

可以看出，在少样本的训练情况下，通过基于图谱信号的特征提取，依旧可以将每种故障模式区分开，在最后测试样本下的滚动轴承故障识别，依旧和训练样本保持高度的一致性，有较高故障识别率。

为了进一步说明该方法的优越性，选择8个时域特征指标，分别为均值指标、均方根指标、峰峰值指标、偏度指标、峰度指标、波形因子指标、峰值因子指标以及裕度因子指标。

依旧计算每两类的双样本Z值，按照同样的方法选择本次故障特征输入向量，通过计算得到，最终选取均方根值指标、峰度指标以及裕度因子指标作为本次的故障特征输入向量。将该故障向量输入到SVM诊断模型中，得到的结果与图谱指标计算得到的结果见表2。

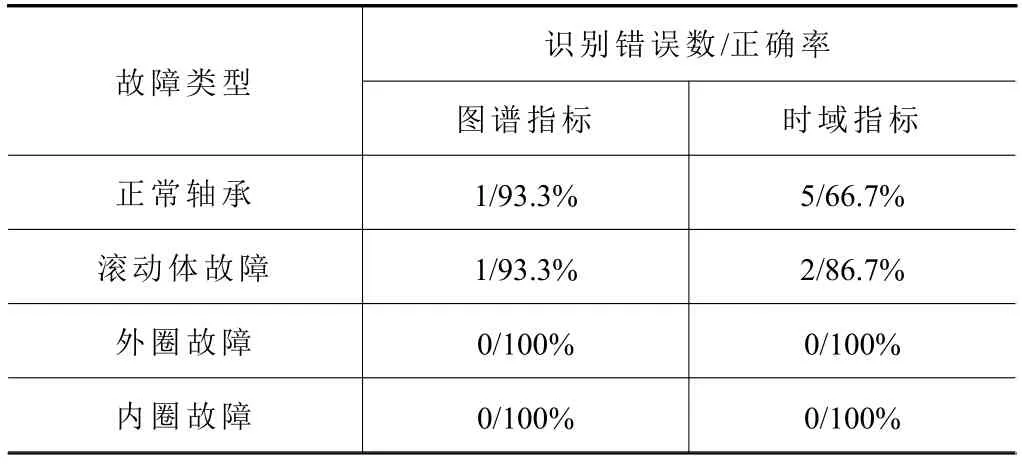
表2 基于不同方法特征提取结果

由表2可以看出，在识别正常轴承和滚动轴承时，根据时域指标进行的特征提取方法存在着一定的识别数目，然而采用基于图谱指标的特征提取方法，在正常轴承和滚动体故障情况下均只有1个识别错误。通过计算得到，采用基于图谱指标的特征提取方法识别正确率为96.67%，而在时域特征提取下的故障识别正确率仅为88.33%，进一步表明基于图谱信号进行特征提取能够准确的捕捉不同滚动轴承故障信息，其特征提取效果优于传统的时域特征提取方法。

3.2 滚动轴承外圈的故障诊断

为了横向验证本文方法的有效性，对滚动轴承的外圈不同故障深度进行故障识别，依旧采用，CWRU电气工程实验室的实验数据[17]，电机轴承故障使用电火花加工来接种，轴承的外圈故障直径分别为 0.177 8 mm、0.355 6 mm 以及 0.533 4 mm。对外圈不同故障直径的滚动轴承和正常轴承的数据进行采集，并分别在4种状态下选取1个样本，其时域波形如图10所示。

图10 滚动轴承外圈不同故障振动信号时域波形图

首先，将80个样本数据全部进行0-1标准化，然后通过公式（1）将振动数据转换成可视图结构数据，得到相应的可视图结构数据后，计算其邻接矩阵和拉普拉斯矩阵，再分别计算得到邻接矩阵特征值和拉普拉斯矩阵特征值。通过计算出的特征值得到表1的9个图谱指标，之后计算每类样本间的双样本Z值，最后选择双样本Z值最大前3个，将其作为故障特征输入向量，最后采用样本为1～5，20～25，40～45，60～65 序列号数据作为训练样本，其余数据作为测试样本。

分别从上述4种状态下的数据各采集20个样本，每个样本长度为2 048，共有80个数据样本。该80个数据样本分成测试样本和训练样本两部分，训练样本取每种状态下的5个数据样本，测试样本取剩余的15个数据样本。准备好训练样本和测试样本后，其故障诊断流程如图4所示。

将滚动轴承振动信号转换成可视图之后，算其邻接矩阵和拉普拉斯矩阵，再分别计算得到邻接矩阵特征值和拉普拉斯矩阵特征值。通过表1中求出相对应的9个图谱指标，分别计算选取特征向量的双样本Z值，如图11所示。

图11 中，a～f分别表示 0.177 8 mm 外圈故障与0.355 6 mm 外圈故障数据的双样本Z值、0.177 8 mm外圈故障与0.533 4 mm外圈故障数据的双样本Z值、0.177 8 mm外圈故障与正常轴承数据的双样本Z值、0.355 6 mm 外圈故障与 0.533 4 mm 外圈故障数据的双样本Z值、0.355 6 mm外圈故障与正常轴承数据的双样本Z值、0.533 4 mm外圈故障与正常轴承数据的双样本Z值。按照上述选择方法，同样选取双样本Z值的最大前3个作为本次的故障特征向量输入。最后选择图能量指标、特征值的平均绝对值偏差指标以及特征值绝对值偏差指标作为本次的故障特征向量。对选取后的特征指标进行三维可视分析，得到图12。

图11 外圈故障不同直径深度的双样本Z值

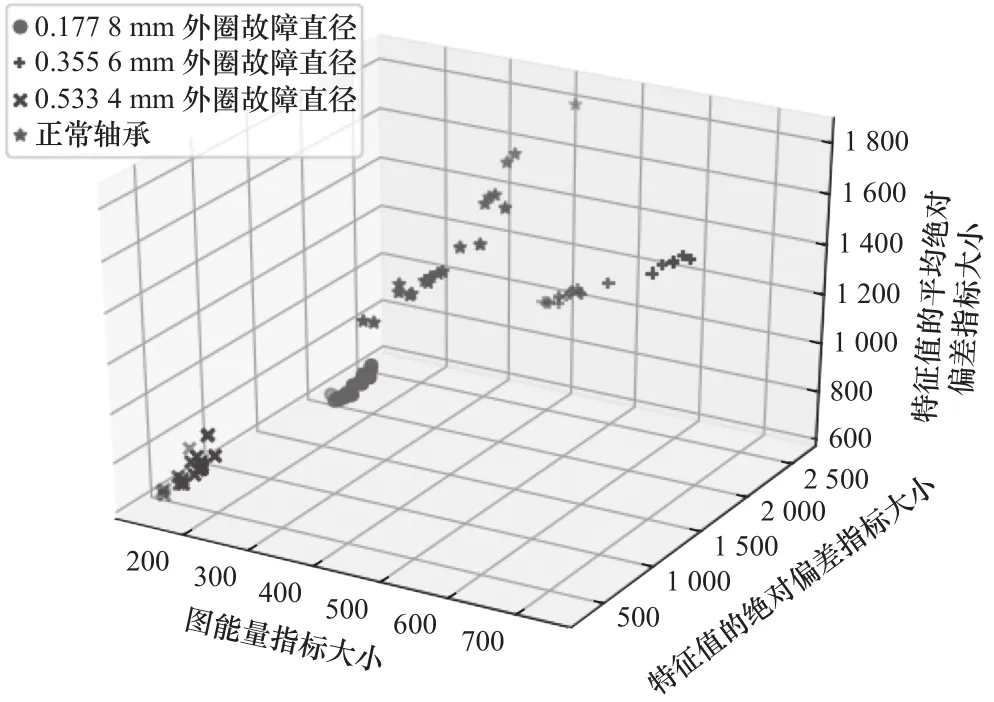
图12 外圈不同故障直径的图谱指标特征值

可以看出，经过图谱特征提取后，0.177 8 mm、0.355 6 mm、0.533 4 mm 外圈故障直径以及正常轴承的特征值有一个比较明显的区分，具有良好的聚集性，而且不同故障直径基本上无重叠现象。总体上来看，通过该方法提取得到的特征展现出较高的类内相似度和较低的类间相似度，更有利于后期的滚动轴承故障识别。

将处理好的训练样本数据作为SVM算法的特征向量输入，由于每一个特征向量大小差异很大，为了消除这种差距，对每一个输入特征采用0-1标准化来减少每一个输入特征之间的差异，将其输入到SVM算法模型中，训练得到最优超平面。将测试样本数据输入到已经训练好的SVM模型中，输出滚动轴承故障类别，最后将测试样本得到的类别与训练样本的已知的类别作为比较，分别如图13和14所示。可以看出，在少样本的训练情况下，通过基于图谱信号的特征提取，依旧可以将每种故障模式区分开，在最后测试样本下的滚动轴承故障识别，依旧和训练样本保持高度的一致性，有较高故障识别率。

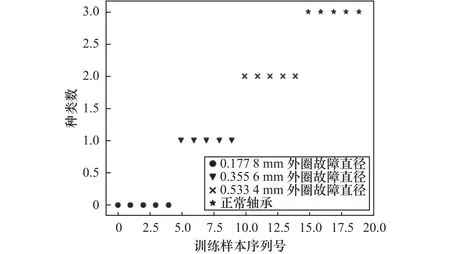
图13 训练样本

图14 测试样本

为了进一步说明该方法的优越性，选择8个时域特征指标，分别为均值指标、均方根指标、峰峰值指标、偏度指标、峰度指标、波形因子指标、峰值因子指标以及裕度因子指标。

通过采用双样本Z值选择本次的故障特征输入向量，通过结果分析，最终选择选取裕度因子指标、峰度指标以及波形因子指标作为本次的故障特征输入向量。将该故障向量输入到故障诊断模型中，与图谱指标得到的结果见表3。

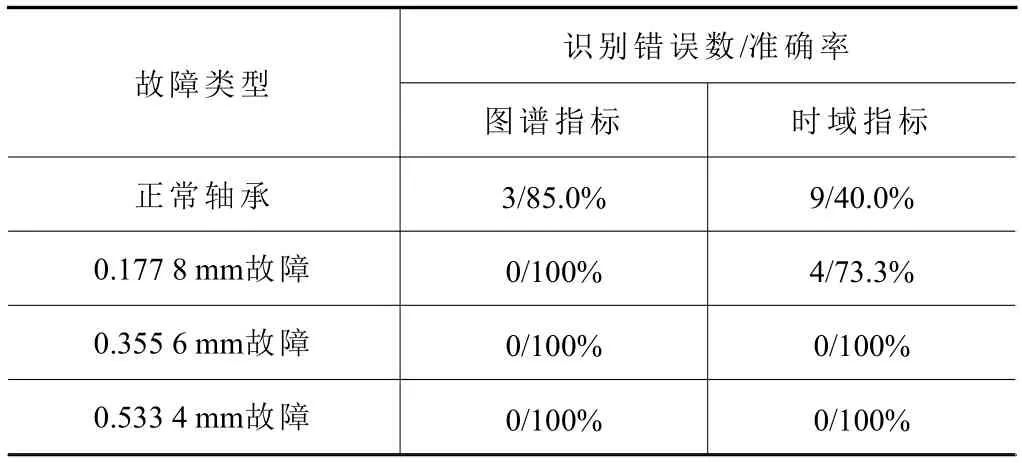
表3 基于不同方法特征提取结果

由表3可以看出，基于时域指标的特征提取方法在识别正常轴承的情况下有较多错误，同时，在识别0.177 8 mm外圈故障下也会产生一定的错误，然而采用基于图谱指标的特征提取方法，只在正常轴承情况下有3个识别错误。通过计算得到，采用基于图谱指标的特征提取方法识别正确率为95.00%，而在时域特征提取下的故障识别正确率仅为78.33%，进一步表明基于图谱信号的特征提取能够准确地捕捉滚动轴承外圈不同直径故障信息，其特征提取效果优于传统的时域特征提取方法。

4 结语

针对滚动轴承传统的故障特征提取方法易受外界的噪声干扰问题，提出一种可视图谱信号特征提取和支持向量机分类的滚动轴承故障诊断方法。主要结论如下：

（1）提出了一种基于可视图图谱特征提取的故障诊断方法，利用支持向量机对特征空间划分最优超平面，并具有较好鲁棒性的优点，精确实现滚动轴承的故障分类。

（2）采用双样本Z值评估特征之间的差异的方法。当特征值的Z值越大时，就能表明区分样本的能力越强，更好地选择出合适的滚动轴承故障特征图谱指标。

（3）将可视图图谱特征提取的方法与传统的时域特征提取方法进行对比，在识别轴承不同故障类型以及轴承外圈不同故障直径正确率分别为96.67%和95.00%，进一步表明基于可视图谱信号特征提取的优越性。