多视角扩思维 深探究提素养——以2021 年浙江卷高考数学第17 题为例

甘肃省兰州市榆中县恩玲中学(730100) 张 科

江苏省南京市金陵中学(210005) 郭建华

向量是沟通代数、几何以及三角函数等知识的一种工具,在处理代数、几何、三角等不同数学分支的问题中,向量起到了纽带的作用,使得解题视角多维和方法多样. 因此,在数学教学过程中,教师应培养学生思维,帮助学生形成批判性、创造性、敢质疑的数学思维品质,达到能够厘清数学知识的来龙去脉、建立数学知识的内在联系、把握数学本质以及更深层次的应用,不断促进学生数学核心素养的培养和落实.

下面笔者对2021 年浙江卷高考数学第17 题从几个不同的视角进行了探究,以期抛砖引玉.

1 真题再现

题目 (2021 年高考浙江卷第17 题) 已知平面向量a,b,c(c ̸=0)满足|a|=1,|b|=2,a·b=0,(a-b)·c=0.记d在a,b方向上的投影分别为x,y,d-a在c方向上的投影为z. 则x2+y2+z2的最小值为.

2 试题分析

该填空题以学生最熟悉的平面向量为数学情境,考查了数形结合、转化与化归、函数与方程等数学思想方法,体现新高考评价体系“四翼”的综合性;测试的核心知识点是平面向量相关知识,最终转化为多元变量最值问题,考查学生逻辑推理素养;试题结构美丽,把平面向量与多元最值问题综合的如此美妙,考查学生数学抽象素养. 本题切入口宽,解法多样,区分度高,能较好地甄别学生的思维水平和提升学生的数学抽象素养,是一道很好的压轴题.

笔者立足数学抽象素养,培养学生提出问题的思维品质,对该题从多视角探索其解法做了一些探究和尝试,现整理成文与读者共飨.

3 解法探究

通过对此题多种解法的探究,不仅让学生获取问题的具体解法,而且还要在顺应学生思维发展规律的基础上注重培养学生提出问题的能力,让学生掌握本题的实质是向量外皮下的不等式问题.

3.1 等价转化,化生为熟

因为a·b=0,所以a⊥b,也注意到|a|=1,|b|=2,则建立直角坐标系xOy,使得a= (1,0),b= (0,2),c= (m,n).因为(a-b)·c= 0, 所以m-2n= 0, 即m= 2n, 于是c= (2n,n)(n ̸=0). 又因为d在a,b方向的投影分别为x,y,所以由向量投影的定义得d= (x,y). 而又d-a在c方向上的投影为z,所以

3.2 多维视角,拓展思维

视角1 消元视角,主客分明

评析 此方法从平面坐标视角求解. 将平面向量问题转化为点到直线的距离问题,即代数问题几何化,利用点到直线的距离公式求出最值,提升学生逻辑推理和直观想象素养.

3.3 高阶思维,以简驭繁

视角8 空间视角,点到面距

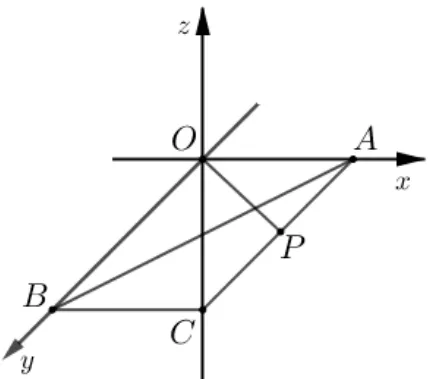
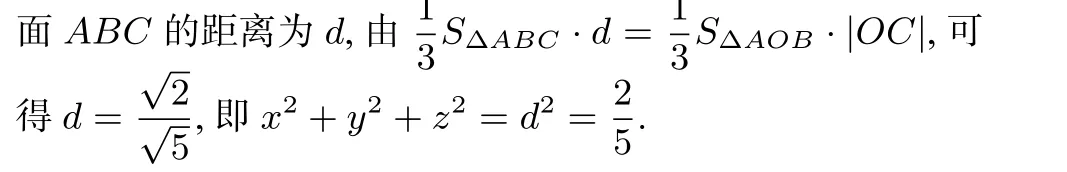
评析 此方法利用空间坐标法将平面向量问题转化为空间向量问题,通过学生空间几何中求点到平面距离常用方法——等体积法求得点到平面的距离,培养学生的高阶思维,促进学生的直观想象素养.

评析 此方法利用高等数学中的拉格朗日乘数法求解.Lagrange 乘数法是高等数学中求极(最)值非常重要的一种方法,在高考中借助高等数学背景考查高中数学知识越来越热门,因此在解决多元函数最值时,巧妙地利用拉格朗日乘数法去解答,不仅可以简驭繁,达到难题巧解的目的,而且还能培养学生的高阶思维,提升学生的“四能”,具有事半功倍之效.

3.4 变式训练,举一反三

设计意图 通过变式训练再次让学生感受同一数学模型的解答过程,提高学生的解题效率,培养学生的发散思维,让学生加深对同一问题的理解,并且把握问题的本质,真正做到“举一反三,触类旁通”,促进学生数学抽象素养的提升.

3.5 归纳总结,揭示本质

一道填空题从不同视角得到多种解法,不由得感慨数学世界的优美和精彩是其它任何一门学科所无法比拟! 数学中解题乐趣是其他人所无法感受到的! 一道题不同的视角会有不同的认识,不同的认识会产生不同的解法. 下面归纳总结多元最值问题的一般解题思路:

4 教学启示

在数学教学中,教师应该引导学生从“解题”到“解决问题”, 从“做题”到“素养”的提升, 笔者认为应做到以下“三点”:

(1)以学生参与为落脚点,打造高效课堂

古希腊哲学家柏拉图曾说:“寓学习于游戏”. 在教学过程中,教师应引导学生立足基础,关注细节,注重通性通法,适当延伸拓展,鼓励学生进行一题多解,在多种解法的比较中,让不同层次的学生选择适合自己实际的解法,尊重学生的差异,让不同层次的学生参与到数学问题解决的活动中,寓学于乐. 上海市特级教师文卫星先生提出“数学生态课堂”: 即数学课堂教学要落实“两个尊重”: 尊重数学知识发生、发展过程,尊重学生认知规律;同时要把握“两个度”: 思想(哲学或数学)高度与文化厚度.[3]因此,在习题课中,教师尽量尊重学生,充分暴露学生思维的“卡壳”,同时要注重引导学生对数学概念、思想、方法的本质的探索和理解,实现学生在课堂上思维的发散性和逻辑的缜密性最大化,优化教学,最终真正打造高效课堂.

(2)以微专题课为生长点,提升思维品质

基于学生的元认知水平和“最近发展区”,以微专题形式展开教学,引导学生加强知识内在联系,突出核心概念的理解应用,体现数学本质,提高学生发现问题、提出问题、分析问题和解决新问题的能力,激发学生的问题意识,在教师的指引下让学生学会用数学的眼光观察问题,用数学的思维思考问题,用数学的语言表达问题,用数学的思想解决问题,进而培养学生批判性、创造性和敢质疑的思维品质.

(3)以问题串教学为着力点,引领素养提升

广东省名师李定平曾提出: 数学新知识的产生是为了解决问题的需要,是在问题解决的过程中进行构建的. 学生在问题解决的情境中形成数学知识, 不仅有助于知识的理解,而且还可以很好的领略数学的精神、思想、方法,同时,发现问题与自我解决问题的能力及数学核心素养也得到了提高.[4]就正如数学家哈尔莫斯所说:“问题是数学的心脏”. 在数学教学中,通过问题串不仅有利于数学知识、数学基本思想方法的梳理与搭建,突破教学重难点,夯实学生“四基”,进而提升“四能”,还有助于开展深度学习、培养学生高阶思维,提升数学核心素养.