2022 年新高考Ⅰ卷函数压轴题多角度解析

广州市华南师范大学附属中学(510630) 周建锋

一、题目及解析

题目 (2022 年新高考Ⅰ卷第22 题) 已知函数f(x) =ex-ax和g(x)=ax-lnx有相同的最小值.

(1)求a;

(2)证明: 存在直线y=b, 其与两条曲线y=f(x)和y=g(x)共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列.

1. 第(1)问解析

2. 第(2)问解析

第(2)问不同于前些年常考的双变量不等式的函数证明题,问法别出心裁,需要仔细分析,结合所学知识求解,没有现成的模式. 这符合新高考重点考查学生分析问题、解决问题能力的宗旨,对学生是个不小的考验.

分析1 在第(1)问的基础上,容易发现f(x),g(x)两个函数有唯一的交点,而且除了有相同的最小值,图象两端向上均可趋于正无穷大,因而有唯一的b ＞1,使得y=b与两条曲线y=f(x),y=g(x)有三个不同的交点,这一点证明并不困难. 其次,要证明从左到右三个交点的横坐标成等差数列,这是本题真正困难的地方.

不过, 注意到x ＞0 时,g(x)=f(lnx),就容易发现y=b与y=g(x) 的两个交点横坐标x2,x3对应的lnx2,lnx3正好也是y=b与y=f(x)的两个交点的横坐标, 因而可以和x1,x2对应起来.

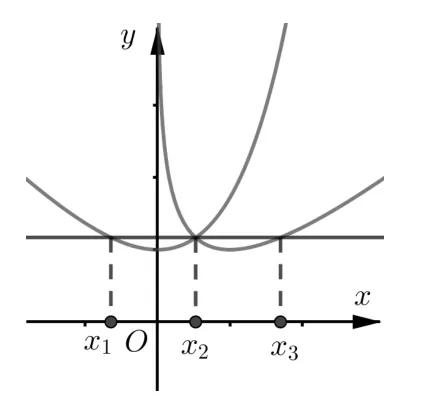
图1

反思1 证法1 是用了同构的思想, 观察f(x),g(x)的结构, 只要将f(x) 中的x替换成lnx, 即为函数g(x) 的结构. 类似的同构思想在函数中较为常见, 如x1ex1=x2lnx2=lnx2·elnx2,左端的x1与右端的lnx2均可作为函数f(x)=xex的自变量的值.

反思2 这种构造的方法是从我们熟悉的极值点偏移入手而得来,学生容易想到,利用f(x2)=g(x2)作为桥梁,寻求证明的路径. 这其中,仍然要用到f(x2) =g(x2) =f(lnx2),但要注意lnx2̸=x2, 所以只能lnx2=x1, 由此即可证明t1=lnt2.

分析3 谈到交点问题, 是一个典型的图形问题, 因而数形结合是一个常见的思考方向. 将y=b与y=f(x)的交点转化为y=x+b与y= ex的交点. 同理,将y=b与y=g(x)的交点转化为y=x-b与y= lnx的交点. 此时发现两对曲线及交点关于y=x对称,四个交点构成矩形,利用对角线互相平分即可证明.

证法3 由前所证,x1＜0＜x2＜1＜ x3, 存在唯一的实数b ＞1, 使得b= ex1-x1=ex2-x2=x2-lnx2=x3-lnx3,即y=x+b与y= ex交于横坐标为x1,x2的两点,y=x-b与y= lnx交于横坐标为x2,x3的两点.

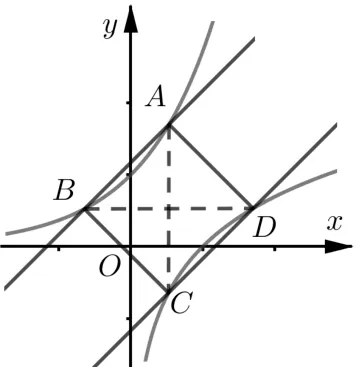
图2

反思3 数形结合是一种重要的数学思想,在本题中巧妙地利用y=x+b,y=ex及y=x-b,y=lnx关于y=x的对称,得到ABCD为矩形,所以对角线互相平分,对角线中点横坐标相等,进而证明了x1,x2,x3成等差数列. 用数形结合方法证明数学问题时,要注意在图形基础上加强逻辑推理,将图形的感性认识上升为理性认识.

二、新高考带来的启示

今年全国高考数学Ⅰ卷被称为近十年来难度最大的一套卷,由本卷的压轴题可见一斑. 明年将是广东新教材实施后的第一年高考,我们应该注意什么呢?

1. 重视教考衔接. 新高考强调考查“一核四层四翼”,“一核”即“立德树人、服务选拔、导向教学”,“四层”即“必备知识、关键能力、学科素养、核心价值”,“四翼”即“基础性、综合性、应用性、创新性”. 总的来说,就是要让学生真正学会运用数学分析问题、解决问题,平常的教学中要全面落实学生的数学核心素养,抛弃“应试教育”、“题海战术”的陈旧思想. 以本题为例,学生之所以难以入手,根本的原因还是习惯了“熟悉”问题的“熟练”解法,遇到新问题就不会寻找问题的关键,不会从数学“通识”角度去理解问题,寻找解决问题的切入点,而本题用到的“同构”、“万能t法”、“数形结合”均是数学“通识”在具体问题中的体现.

2. 要提升学生的核心素养,平常的教学多以学生为本.通过课堂上充分挖掘学生潜能,课后多引导学生研究性学习,锻炼学生运用数学分析问题、解决问题的能力. 在新教材中,数学建模是一个重要模块,要真正以此为契机,开展以此为平台的学习模式.

3. 教师要充分领会新课标、新教材、新高考,不断提升自己,同时也给学生树立终身学习的榜样. 身教重于言传,一个固步自封、不思进取的教师,很难培养出积极向上、学业优秀的学生. 教师的学习来于教材更要高于教材,才能给学生更好的引领.