球内接n 棱锥体积之最值问题研究与教学启示

华南师范大学数学科学学院(510631) 陈伟连

外接球问题是高考的高频考点,仅近三年的全国卷就一共考查了4 次. 为突破该考点,通常将其作为一个专题进行复习,而2022 年新高考Ⅰ卷第8 题就属于该专题的范畴. 本文对本道题进行分析,并给出该题的多种解法. 接着对本题条件进行特殊化变式探究和一般化变式推广,研究球的内接棱锥体积何时取得最大值和最小值. 最后,根据对本题的研究提出一些教学启示,为一线教师和高三学生备考提供一些思路和帮助.

1 试题呈现

2 试题剖析

本题以正四棱锥的外接球为载体,考查了球心到截面距离的勾股关系、余弦定理、三角函数、四棱锥的体积、球的体积、三次函数的最值等基础知识. 能力素养层面主要考查了空间想象、逻辑推理和数学运算能力,体现了函数与方程、化归的思想方法. 试题的设置简洁明了,但跨度较大,要求学生有较强的问题分析能力和扎实的数学基础. 此外,本题解法多样,学生能够从不同的角度入手,可以较好地检验学生对基础知识和基本思想方法的综合运用能力,具有较高的区分度.

本题的解题思路主要分为四步: ①求出球的半径,明确球内接正四棱锥中的三个直角三角形: RtΔPAO′,RtΔOAO′,RtΔAO′B和等腰ΔPOA(如图1); ②用字母表示相关的边长和角度,构造正四棱锥体积的表达式; ③寻找各字母之间的数量关系,将多元降为一元; ④换元,并利用导数求正四棱锥体积的最小值和最大值.

图1

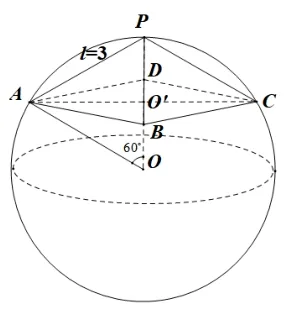
图2

图3

3 试题解答

3.1 设边法

解法二 (以侧棱长的平方为变元) 根据题意易求球的半径为R= 3. 设正四棱锥的高为h,底面边长为a(如图4),于是根据勾股定理可构建如下方程组:

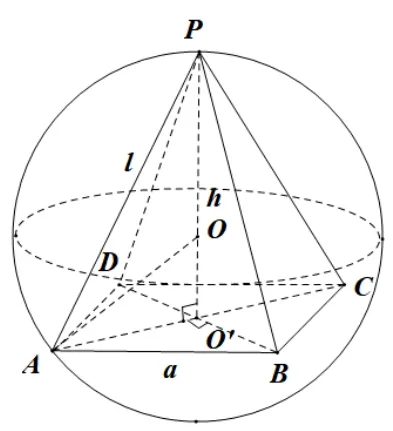
图4

3.2 设角法

4 试题推广

评注 变式1 将四棱锥改为三棱锥,保持球的半径不变.根据求解过程可知,正三棱锥体积取得最值时的侧棱长与正四棱锥体积取得最值时的侧棱长相等. 于是提出猜想: 球内接正n棱锥的体积取得最值时的侧棱长只与球的半径有关,与n的值无关. 接下来将条件一般化进行推广探究,探究其中蕴含的本质知识.

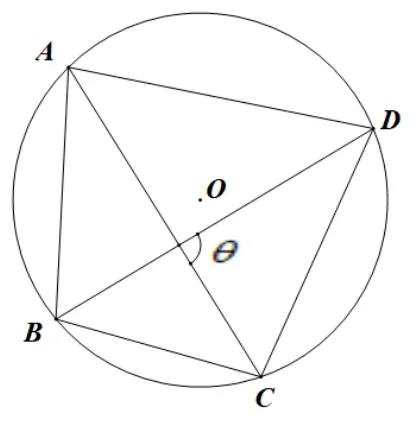
图5

5 教学启示

5.1 采取“微专题”复习,实现考点突破

“微专题”复习是指围绕复习的重点和关键点设计的、利用具有紧密相关性的知识或方法形成的专项研究,或者结合学生的疑点和易错点整合的、能够在短时间内专门解决的问题集[1]. 这种复习方法比较灵活,可以基于试卷评讲拓展,和大专题复习相结合,有利于促进学生对数学概念与原理的理解. 例如,评讲本道题时便可以采取“微专题”复习法,通过设置问题串,发挥学生的主体性,引导学生从特殊到一般进行主动探究,发现正n棱锥的体积取得最值时侧棱的长度与球半径的关系,突破该考点.

5.2 一题多解发散思维,多题一解总结方法

一题多解有利于加深对知识的理解,渗透数学思想方法,有利于提高思维能力,培养创新意识,有利于调动学习兴趣,培养主动探究的精神[3]. 对本道题进行一题多解解题教学,有利于学生重温球内的勾股定理、余弦定理和棱锥的体积公式等基本知识,更重要的是看到了知识的内在联系,从整体上把握解决求球的内接正棱锥体积最值的一些基本方法,促进认知结构的完善. 但是一题多解之后,应引导学生对各种解法的思维过程进行再认识,对其进行分析、比较和概括,提炼出典型的和可迁移的解题方法. 而多题一解旨在找到求体积最值的通性通法,做到举一反三[3],如解法二便是解该类题的通法.

5.3 注重变式探究,把握数学本质

鲍建生等学者认为,变式教学是有效教学的中国式经验,这是一种有意义的学习[4]. 其中,过程式变式教学策略——铺垫,和脚手架功能类似. 在对本题进行教学时,可以参考试题推广的研究过程,从正四棱锥到特殊化变式为正三棱锥,再一般化推广到正n棱锥,最后推广到普通四棱锥. 通过转化用变式2 的结论解决变式3 的问题,经过层层铺垫,引导学生认识球内接n棱锥体积何时取到最大值的本质.

5.4 渗透模型思想,体会数学概括之美

弗赖登塔尔认为,学数学就是学数学化,教数学就是教数学化. 何小亚教授认为数学具有精确、严谨、简洁、概括和统一的特点. 其中, 最精彩的是概括性, 即能够以一个有限的模式驾驭无穷的具体[5].《义务课程标准(2022 年版)》和《普通高中课程标准(2020 年修订)》都分别将模型意识、模型观念和数学建模作为数学核心素养,可见模型思想的重要性[6-7]. 他们都属于数学化的范畴,其中垂直数学化指从现有的数学世界中抽象概括出更高级的数学模式的过程,是从低层数学到高层数学的过程[8]. 例如在本题的解题教学中就可以在一般化推广后渗透模型化思想,引导学生体会数学的概括之美.