立体几何中的动态问题*
广东省中山市第一中学(528403) 孙要强
1 概述
立体几何是高考的重要考点之一,历年考题题型、难度、结构及分值相对稳定,选填题主要考查概念辨析、位置关系探究、空间几何量的简单计算等,解答题多以简单几何体为载体,考查线线、线面、面面的位置关系. 其中作为压轴成分出现的选填题多涉及到动态问题.
立体几何动态问题注入了某些变化的点、线、面等元素,常常集知识的交汇性与综合性、方法的灵活性与多向性、思维的变通性与深刻性于一体,使立体几何问题更富思辨性、开放性和挑战性. 试题通过考查点、线、面元素位置关系的变化,如翻折、平移、旋转、射影等,引导以动态的眼光去发现问题的本质,有助于培养学生自主探究能力、创新能力和发散性思维.
立体几何的动态问题中的“不确定性”与“动感性”往往成为学生思考与求解问题的思维障碍,具有策略性、挑战性与创新性等特点. 本文从点动、线动和面动三个方面对其进行探究,以期交流研讨.
2 动态问题探究
2.1 点动问题

思路分析 如图2 所示: 沿着侧棱V A把正三棱锥V-ABC三个侧面展开在一个平面内, 则AA′即为截面ΔAEF周长的最小值,在ΔV AA′中,∠AV A′= 3×40°=120°,由余弦定理可得


图2

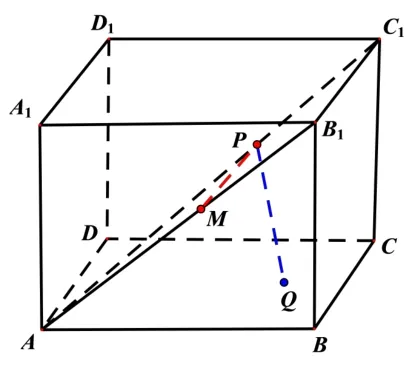
图3


图4
本题组主要研究目标随着空间某些点的变化而变化的问题,简称点动问题. 运动根源是多个点在运动,采用了控制变量法. 研究立体几何中的线段和最短问题,往往需要将几个线段转到一个面中,一般需要进行翻转,再利用点共线,或者点到直线距离进行求解. 这是转化与化归的思想,包含空间问题平面化,折线问题转化为直线段问题,控制某些变量,寻找运动根源等方法.
2.2 线动问题
例2 在等腰梯形ABCD中,已知AB=AD=CD=1,BC= 2,将ΔABD沿直线BD翻折成ΔA′BD,如图5,则直线BA′与CD所成角的取值范围是.

图5

图6

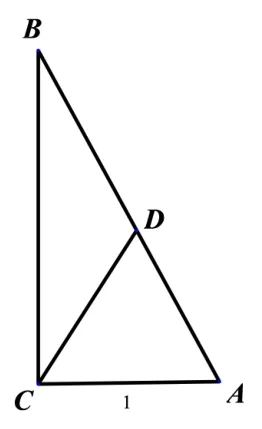
图7
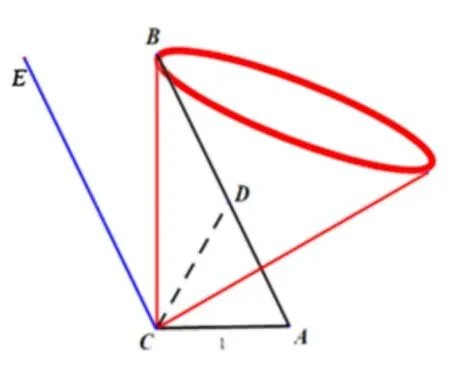
图8

本组题主要研究目标随着空间某条线的变化而变化的问题,简称线动问题. 题组考查是两条动态的异面直线所成角(垂直即夹角为90°),由于直线是不固定的,所成角不易确定,但在研究异面直线所成角时,平移直线不影响直线之间的夹角,进而转化为研究圆锥中母线与直线所成角的问题.
2.3 面动问题
例3 如图9,在四棱锥P-ABCD中,底面ABCD是梯形,AD//BC,AD=2BC,PA⊥PD,AB=PB=1.

图9
(1)证明:PA⊥平面PCD;
(2)若BC=CD= 1,当四棱锥P-ABCD的体积最大时,求直线PB与平面PAD所成角的正弦值.

图11
思路分析 (1)如图10,取AD,AP中点E,F,连接BE,BF,EF. 由AB=PB,PA⊥PD得PA⊥BF,PA⊥EF,又BF ∩EF=F,所以PA⊥平面BEF. 易知平面BEF//平面PCD,所以PA⊥平面PCD.

图1

图10

本题主要研究目标随着空间某个面的变化而变化的问题, 简称面动问题. 题目使用静态语言叙述一个动态的翻折过程, 需要用运动变化的观点看问题, 在平面PAC中,PA⊥PC, 点P在以AC为直径的圆上运动, ΔABE沿着BE翻折,用运动变化观点看待,静态与动态相互转化.
3 结束语
动态立体几何在变化过程中总蕴含着某些不变的因素,问题的解决需要把其变化过程充分地展现出来,观察它的变化规律,寻找不变的静态因素,找到解决问题的突破口,也可以利用极限思想找到极端位置,用特殊法求解. 对于探究存在问题或动态范围(最值)问题,用定性分析难以解决时,可以引进参数,通过构建方程、函数或不等式等进行定量计算,以算促证.
“动”与“静”是事物的两个方面,从点,线,面等不同角度研究立体几何中的“动”,寻求其“静”,以“静”制“动”,以不变应万变,凸出几何本质,提升思维能力,培养数学核心素养,彰显育人功能.

