例谈运用科学思维指导学生解决渗透装置再次平衡难题

安徽 谢四军 徐金鹏

利用渗透装置研究渗透作用所需条件，可类比为研究动、植物细胞发生渗透作用的结构基础，这对于践行结构与功能观等生命观念至关重要。很多年来一直有一些试题围绕渗透装置再次平衡问题进行设计，而市面上多数试题的答案和解释不是处理粗糙，就是认识片面甚至是错误的，这给教师教学和学生学习带来很多困扰。笔者发现，在教学中运用科学思维建构物理模型并结合“假说—演绎法”可理性解决此类问题，喜获良好效果。

一、高中生物学教学中出现渗透装置再次平衡难题的原因

高中生物学学习中出现渗透装置再次平衡难题的原因主要有以下几点：(1)此系统为物理装置，需要利用物理学中液体压强产生的压力和渗透压力平衡等原理解决。部分生物学教师畏难于解决跨学科的问题，且认为在生物学课堂上花大力气解决物理学难题没有必要。(2)部分教师对待此类问题采取“人云亦云”的思想，即没有深入思考和分析，而是简单借用网络或已有试题和答案应付教学。(3)很多学校生物实验室没有配备渗透装置，无法利用实际实验研究此类问题；部分教师认为即使开展实验，实际效果也未必明显。鉴于上述原因，很多教师对于渗透装置再次平衡问题理解不清，故而出现讲解不透彻的情况，甚至只是告诉学生记住相关答案即可。教师粗线条或模糊化处理此类问题显然对于学生科学理解此类问题是不够的，也让学生难以有效打破学科间壁垒而形成质朴的科学观和自然观。

二、渗透装置再次平衡典型例题呈现

渗透装置设备简单，通常由铁架台、大烧杯、漏斗、玻璃纸(或其他半透膜)、清水和一定浓度蔗糖溶液组成。实验中漏斗广口裹上玻璃纸，并在漏斗中加入一定浓度蔗糖溶液，而后放入盛有清水的烧杯中，因半透膜内外溶液渗透压力不同，使清水渗入漏斗而出现液面升高并最终维持在一定高度(假设内外液面高度差为h1)的渗透现象(即渗透装置初次平衡)。一些试题在此渗透装置初次平衡后改变条件，讨论渗透装置再次平衡时内外液面高度差h2，并比较h1和h2的大小关系。梳理可知，初次平衡后通常改变的条件有：(1)烧杯中加入适量水；(2)烧杯中吸去适量水；(3)漏斗中加入适量水；(4)漏斗中再加适入量蔗糖溶液(或蔗糖)；(5)吸去漏斗中高出的液面差h1。

【例题】图1为平衡时的渗透装置，烧杯内的液面高度为a1，漏斗内的液面高度为b1，液面高度差为h1=b1-a1。在此基础上继续实验，以渗透平衡时的液面差为观测指标，下列叙述正确的是( )

图1

A.若吸出漏斗中高出烧杯内液面的溶液，则平衡时h1增大

B.若向漏斗中加入少量蔗糖，平衡时h1将增大

C.若向漏斗中加入适量且与漏斗内的蔗糖溶液浓度相等的蔗糖溶液，则平衡时h1不变

D.向烧杯中加入适量清水，平衡时h1将增大

【参考答案】B

这是网络上或教辅资料中常见的一道关于研究渗透装置再次平衡的试题。此类问题中，吸出漏斗中高出烧杯内液面的溶液，再次平衡时h2比h1小；向漏斗中加入少量蔗糖或蔗糖溶液，再次平衡时h2比h1大，这些情况学生比较容易理解。向漏斗中加入适量清水、向烧杯中加入适量清水或者烧杯中吸去适量水，再次平衡时h2与初次平衡h1的大小关系，很多学生难以理解。究其原因，还是与课堂上生物教师未能讲清渗透装置平衡的基本原理，未能通过建立物理模型正确引导学生采用科学思维方法分析有关。本文主要围绕渗透装置初次平衡后向漏斗中加入适量清水引起的再次平衡的难题进行讨论。

三、渗透装置中液面保持平衡的基本物理学原理

教学中教师需要向学生讲清渗透装置保持平衡实际上为液体间力学平衡的结果。以漏斗广口上裹着的半透膜为研究对象，实验中其受两个方向不同的力的作用，一是漏斗外清水与漏斗内蔗糖溶液间浓度差形成的方向向上的渗透压力，二是烧杯和漏斗间形成的液面差会产生对半透膜方向向下的压力，实验中由于漏斗口面积不变，可简单用烧杯和漏斗间形成的液面差大小代表对半透膜产生的压力大小，学生能够理解。装置初次平衡后向装置漏斗中加入适量清水，显然会改变半透膜内外渗透压和液面差产生的压力，系统再次平衡时半透膜两侧仍然是受力平衡。漏斗中加清水后，渗透压变小而液面高度差增大，此时漏斗液面会下降。漏斗液面下降会导致渗透压力增大，同时高度差产生的压力减小，烧杯中液面也会有所上升。究竟液面下降到何处时装置会再次平衡？再次平衡时液面差h2与h1相比究竟是增大、减小还是不变？在课堂上不能进行实验探究的条件下，一些教师陷入了教学困境。

四、利用物理模型和“假说-演绎法”解决难题

运用科学思维解决生产或生活中遇到的问题，既是生物学学科核心素养对学生的要求，也是学生解决实际问题所体现的能力和品质。教学中笔者通过引导学生结合渗透装置，以向漏斗中加适量清水为例，画出物理模型，并结合假说-演绎法让学生比较、演绎推理结果与实际结果间的关系，从而得出科学结论，达到“以理服人”的教学效果，学生收获知识的同时也训练了科学思维。具体如下。

分析时，假设渗透装置初次平衡时烧杯内的液面高度为a1，漏斗内的液面高度为b1，此时h1=b1-a1，这种情况下半透膜两侧浓度差产生的渗透压力与液面高度差产生的压力平衡，这是初次平衡的原理(图2甲)。接着，向漏斗中加入适量清水，如图2乙所示，教师提问学生，漏斗加水后的最初液面能否保持不变，学生简单思考后认为不能，并指出渗透压力变小而液面高度差形成的压力增大，不能维持加水后最初液面高度。既然渗透装置不能平衡，那么实验中漏斗中液面需下降而烧杯中液面需要上升才能再次平衡。那么再次平衡时h2与初次平衡时h1究竟有何关系呢？

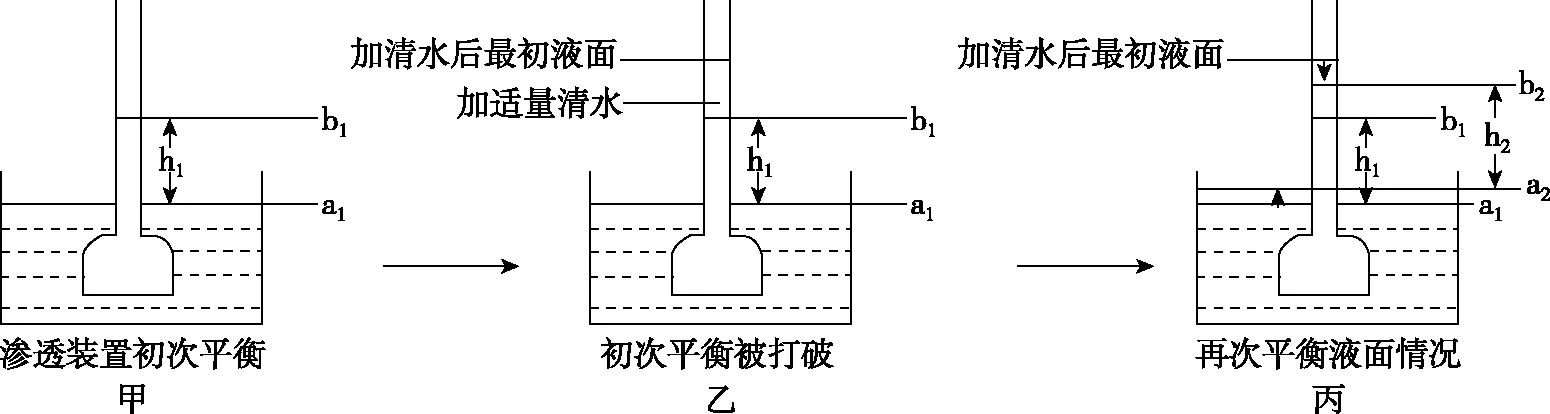
图2

不愤不启，不悱不发。既然良好教学环境已经形成，这便是训练学生利用科学思维解决实际问题的良机。这时教师引导学生针对上述问题提出自己的假设，不同学生提出了不同的观点。笔者继续利用图2丙物理模型进行分析，假设再次平衡时漏斗液面高度为b2，烧杯液面高度为a2，即再次平衡时h2=b2-a2。而比较h2与h1的大小关系，其实可以通过比较(b2-b1)的差值与(a2-a1)的差值关系确定。

接着引导学生按照自己的假说并结合图2丙进行演绎推理：若认为再次平衡时h2与h1相等，可推理出(b2-b1)=(a2-a1)，这时可推导出液面高度差不变，即对半透膜产生向下的压力与初次平衡时一样，结合图2丙可推理出漏斗中总液体量增加，即蔗糖溶液浓度降低，漏斗内外浓度差比初次平衡时减小，即得出再次平衡时渗透压力比初次平衡时减小。这种情况下演绎推理出的结果是半透膜两侧的力不能保持平衡，这与实际结果中渗透装置已经再次平衡产生矛盾，学生很快得出结论，h2与h1相同的假设显然不能成立，即这种结论是错误的。若认为再次平衡时h2大于h1的话，学生仍可按照这种假设进行演绎推理，可推导出图2丙中(b2-b1)>(a2-a1)，此时可分析出再次平衡时高度差产生向下的压力比初次平衡时大，而漏斗中实际液面比初次平衡时高，即意味着漏斗中蔗糖溶液浓度比初次平衡时低，这种状态下半透膜内外渗透压力比初次平衡时小，这种推理结果是h2大于h1时装置不能保持平衡，显然与实际上渗透装置已经达到平衡相矛盾，学生很快归纳出这种假设也是不可能成立的。对于认为h2比h1小的观点，学生按照这种假说很快推理出渗透装置再次平衡时，利用图2丙物理模型可推导出(b2-b1)<(a2-a1)，即高度差减小后产生向下的压力比初次平衡要小，而漏斗中蔗糖液体量增加，蔗糖浓度减小产生的渗透压力与初次平衡时也变小，这种情况下装置才可能再次平衡，与实际情况下装置已经平衡吻合，比较可知这种假说成立。

学生经过分析物理模型，比较两次平衡时烧杯中液面高度差与漏斗液面高度差的关系，利用“假说-演绎法”进行推理分析，科学比较演绎推理结论和实际实验结果的关系，解决问题的同时也顺理成章得出科学结论。这种结论是学生通过真思考、真推理和真比较所获得的，自然是学生能够接受和认可的。分析完向漏斗中加少量水这种条件引起的再次平衡后，很多学生又兴趣盎然地分析向烧杯中加少量水或吸去适量水等再次平衡难题，并很快得出正确结论。古语云：“授人以鱼，不如授人以渔。”现在看来，教学生答案和知识，不如教他们思考问题的方法和解决问题的途径，这样才能让学生真正具有处理复杂问题和解决实际问题的能力。