非光滑表面减阻研究进展
秦立果,龚朝永,孙红江,席奂,Fagla Jules Mawignon,郭飞飞,董光能
(1.西安交通大学 a.现代设计及转子轴承系统教育部重点实验室b.设计科学与基础部件研究所 c.热流科学与工程教育部重点实验室,西安 710049;2.西安工程大学 机电工程学院,西安 710048)
众所周知,流动阻力是流动边界上的物体对流动流体的作用力,这是由于物体的物理尺寸阻碍并改变了流体的流动行为而造成的。自然界中的流体总存在黏性,因此可将流动阻力分为压差阻力和摩擦阻力。已有研究表明,飞机在飞行过程中表面摩擦阻力占总阻力的20%~40%,这引发了巨大的燃料消耗[1]。船舶运行所受的流体阻力主要为表面摩擦阻力,对货船而言,表面摩擦阻力超过了总航行阻力的60%[2]。在水下运动的鱼雷和潜艇表面摩擦阻力可达总阻力的70%。而在长输管道中,泵站的动力几乎全部用于克服管道内表面的摩擦阻力[3]。因此,通过减小摩擦阻力来提高船舶航行速度或减少燃料消耗是当前亟需解决的问题。
如图1 所示,Luo 等[4]对湍流中各种表面减阻技术进行了综述,将壁面减阻类型分为聚合物添加剂减阻、边界层控制减阻和复合减阻三大类。聚合物添加剂减阻通过向湍流流场中释放高分子聚合物,从而降低湍流猝发的频率和强度,实现表面减阻。聚合物添加剂减阻机理尚未完全明确,其中代表性的观点包括添加剂改变湍流结构,降低湍流强度,减少能量损失实现减阻[5-6];降低湍流轴向和径向脉动相关性,减小雷诺应力实现减阻[7-8];添加剂流体的黏弹性和湍流旋涡相互作用实现减阻[9];在湍流边界层中聚合物分子受到拉伸而取向,引起应力各向异性实现减阻等[10]。边界层控制减阻根据表面类型的不同,分为非光滑表面减阻、超疏水表面减阻、微气泡减阻、柔性壁面振动减阻和壁面加热减阻等。其中非光滑表面减阻由于其独有的特点已成为表面减阻技术的研究热点,受到全球学者越来越多的关注。复合减阻是将两种或两种以上的减阻技术有机组合从而实现减阻效果的提升。如常见的沟槽表面减阻和聚合物添加剂减阻的组合,有研究表明这种组合起来的减阻效果不是单单的1+1 叠加,而具有显著放大单一减阻技术的效果[11]。
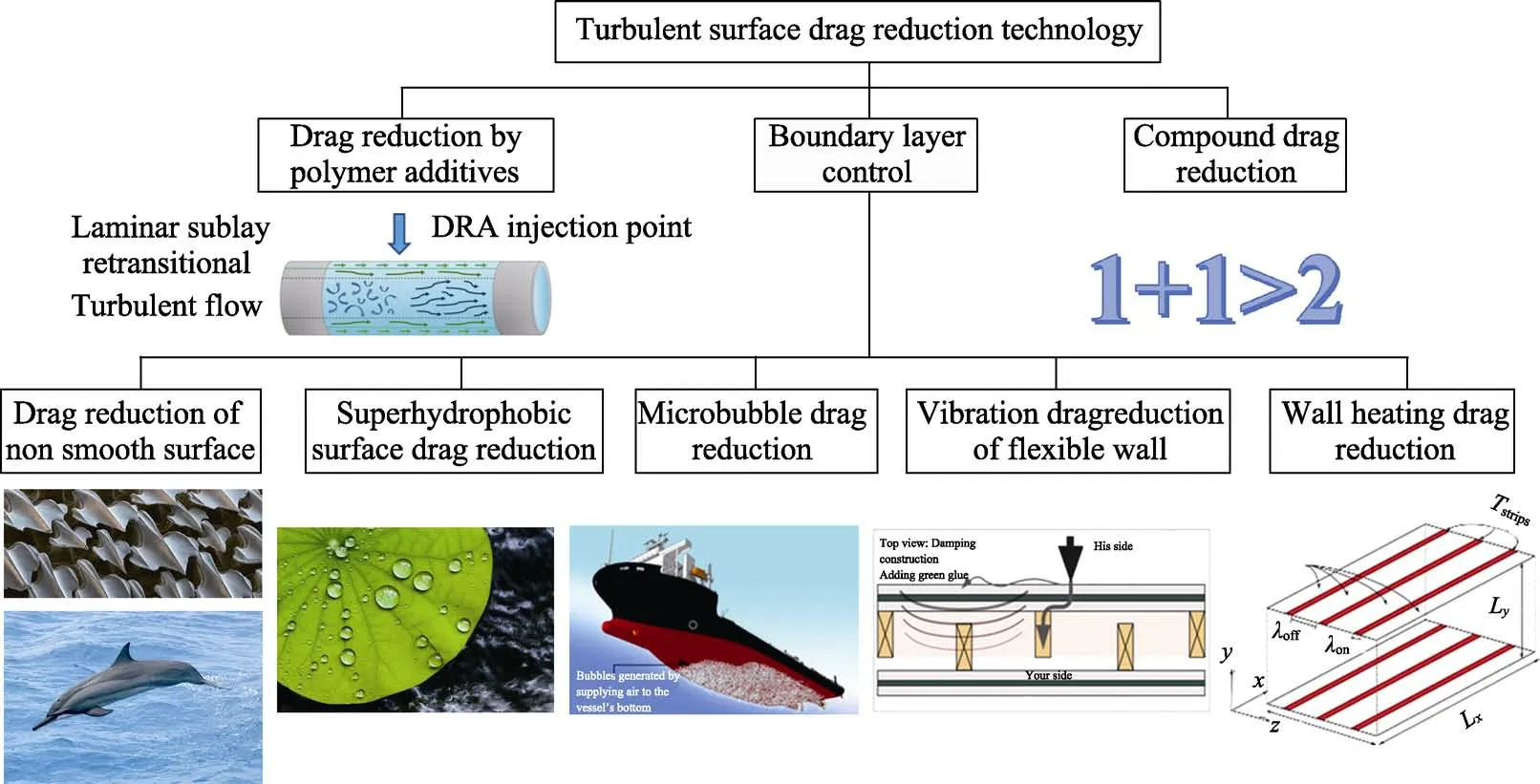
图1 湍流减阻技术[4]Fig.1 Different drag reduction technologies in turbulence[4]
生物体经过亿万年的进化,已形成了适应自身环境的体表结构,其表面阻力非常低,如鲨鱼、海豚或具有黏液的鱼类,其表面是减少阻力的典型代表[12]。非光滑表面减阻是基于仿生学的设计,在光滑表面上制造出类似生物体表的微结构以达到减阻的功效。其减阻效果仅取决于表面特性,不需要附加设备、额外能量消耗及空间占用,更不会对流场造成污染,甚至设计制造的成本也相对较低,故在各种减阻技术中被认为是最有前途的减阻方法。因此,本文主要就此种减阻方法做系统阐述,总结了表面阻力测定的一般方法并重点分析了3 种非光滑表面——沟槽(Riblet)、凹坑(Dimples)和自适应表面(Compliant Wall)的减阻行为与机理,最后对非光滑表面减阻的未来发展方向进行了展望。
1 非光滑表面减阻的研究方法
1.1 湍流边界层减阻的理论推导
在阻力的理论计算研究中,Bache 等[13]通过测量流速分布,利用边界层动量积分公式计算了减阻效果,计算过程如式(1)—(3)。边界层动量损失厚度的定义为:

1.2 非光滑表面阻力测量方法
针对可压缩和不可压缩流体,非光滑表面阻力测量的试验方法可分为风洞和水槽试验。根据非光滑表面所处位置,即内、外流场,又可将测量试验分为开放式和封闭式[16]。在开放式试验条件下,表面阻力通常采用力平衡法和尾迹移测法来确定。对水、油或空气等介质一般采用力平衡法,而风洞中测定机翼的阻力则采用尾迹移测法。
力平衡法测阻原理如图2 所示。样品安装在力平衡装置上,浸没到流体中(一般为水或油),如图2a 所示。流道的设置如图2b 所示,也称之为“柏林油道”[17]。该方法要求对转子进行设置实现流体的恒速流动,然后进行阻力测量。
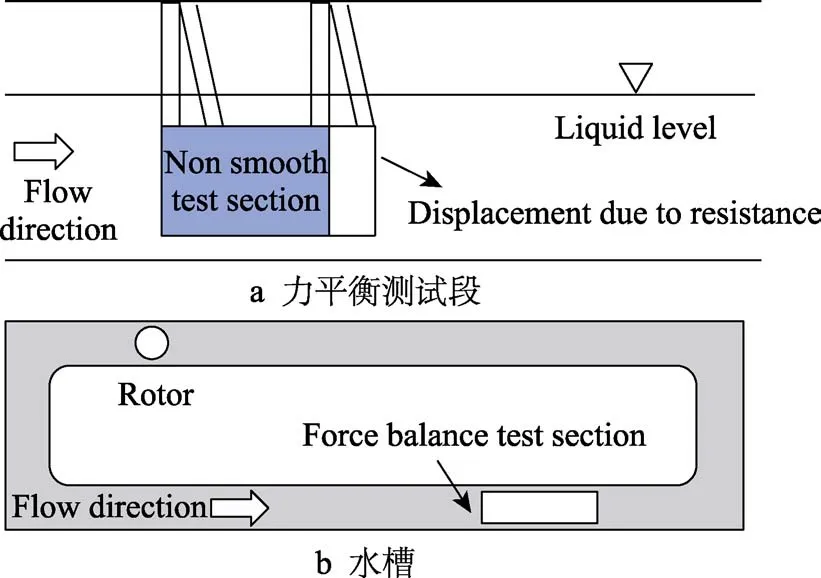
图2 水/油槽力平衡测试方法示意图Fig.2 Water or oil force balance method: a) force balance test section; b) water or oil tank facility
尾迹移测方法如图3 所示,尾迹移测探针测定压力,利用尾迹压力曲线计算速度,再积分获得阻力系数(Cd),从而计算得到减阻率。非光滑表面位于管道内侧时,其减阻率可用式(4)表示。
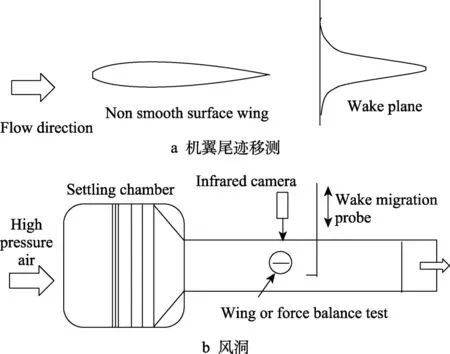
图3 尾迹移测法示意图Fig.3 Wake traverse method: a) airfoil experiments;b) wind tunnel facility

式中:τΔ 为光滑表面的壁面剪切力0τ与非光滑表面剪切力τ之差,pΔ 为光滑管道压差值p0与非光滑管道压差值p之差,此方法也称之为封闭式的阻力测定。如图4a 所示,可用压差计获得测试段的压力差。由于非光滑表面在尺寸较小的封闭式管道中的加工较为困难,研究者们又提出了分离式管道的测试方案,如图4b 所示,左侧是一个圆形分离式管道,右侧显示了一个类似三明治设计的矩形通道,管道或通道的一侧设计有非光滑的减阻结构,当流体流经样品测试区域时,使用压力计测量两点之间的压差,计算得到减阻率。
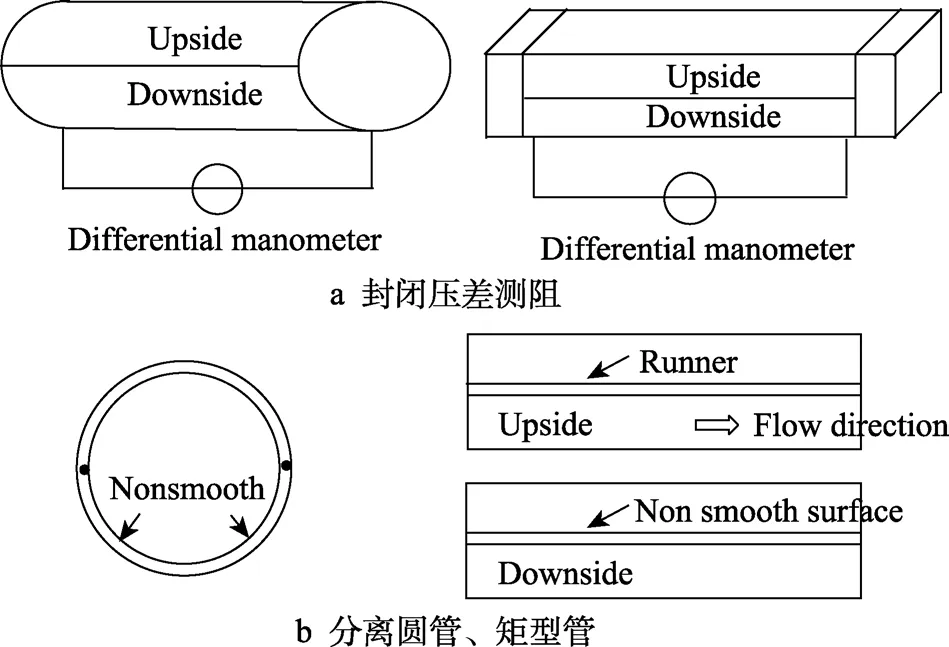
图4 封闭式阻力测定试验和仪器[16]Fig.4 Closed channel methods and apparatuses:a) drag measurement via pressure drop; b) split designs of pipe and rectangular channel[16]
1.3 流场速度测量与可视化
在非光滑表面湍流减阻特性的测量中,平均速度剖面法是评价壁面摩擦阻力的重要方法。空间单点时间序列测量技术可获取流向平均速度沿边界层法向分布剖面,实现高时间分辨率测量,许多研究者采用热线测速法(HWA)对非光滑壁面附近的流场速度进行测量[18-19]。随着流体力学测速方法的不断发展,粒子图像测速法(PIV)作为一种瞬态、多点和无接触式的测速方法而被广泛使用。PIV 是通过测量示踪粒子在单位时间的位移来间接地反映流场的瞬态速度分布,测量精度高。如Lee 等[20]采用直径为1 µm的橄榄油作为示踪粒子,对机翼沟槽表面的外流场进行了速度测量,获得了瞬时速度场并由此计算出了湍流动能。Campenhout 等[21]利用PIV 技术获得了凹坑平板上的速度剖面,以及凹坑内部的速度分布,计算获得了湍流边界层的大量信息。此外,为了使流动可视并实现流体的流动图像记录,就须用流动显示技术[22]。应用最为广泛和成熟的是示踪粒子流动显示技术。该技术向流体中加入一定量微小尺度(直径几十纳米到几十微米)的示踪粒子,采用高速摄像头拍摄和跟随粒子在流体中运动的轨迹来显示流动结构和流动现象,并生成流动图像,最后借助计算机和数字图像处理技术,获得较为全面的流场信息。
1.4 数值模拟方法
与试验测量相比,数值模拟法具有易实现、灵活性高和成本相对较低的优点,这在自适应表面的研究中体现尤为突出。然而数值模拟需要求解边界层内部的湍流结构,因此数值计算较试验研究更为复杂。在小尺度、简单几何模型、低雷诺数的流动研究中多采用直接数值模拟(DNS)和大涡模拟(LES)2 种方法。如早期Choi 等[23]和Lienhart 等[24]利用DNS 对沟槽参数流动结构的影响研究,以及在判断凹坑表面是否具有减阻效果时与试验研究并行开展的DNS 模拟。Duan 等[25-26]对沟槽表面在高音速和超音速条件下做了直接数值模拟,尽管他们对DNS 和LES 的应用范围做了一些扩展,但由于计算成本巨大,DNS和LES 很少应用在高雷诺数和复杂几何的研究中,工程应用尤为困难[27]。因此,在特定的条件下对控制方程进行统计平均的雷诺平均(RANS)湍流数值模拟成为很好的解决方案。采用Boussinesq 假设的涡黏模型使得计算进一步简化,这在湍流减阻研究中得到较好的应用,如在机翼非光滑表面等可压缩流动计算中k-ε方程的大量应用以及复杂几何模型的沟槽表面减阻研究中k-ω方程的修正应用[28-29]等。
2 沟槽(肋条)表面减阻
2.1 沟槽的概念及无量纲特征参数
肋条(Riblets)是由光滑表面上的小突起与流动方向上的纵向微槽组成[30],已被证实可以减小湍流的壁面摩擦阻力,并在航空和海洋行业得到了较好的应用。肋条减阻的设计灵感来自鲨鱼鳞片表面上的齿状结构,也被称为盾鳞。该结构可以提升体表附近的流体涡旋从而降低阻力。图5 是采用SEM 拍摄的在水中能快速运动的典型生物代表(灰鲭鲨和白斑角鲨)的表面微观形貌。观察发现灰鲭鲨的每个盾鳞上有5个肋条且肋条之间的间隙很小,盾鳞排布密实,几乎没有空隙。而白斑角鲨的每个盾鳞上只有3 个肋条且盾鳞之间的间隙相对较大[31]。对大多数鲨鱼而言,盾鳞的尺寸一般为0.2~0.5 mm,间距为30~100 µm[32]。

图5 鲨鱼皮表面的扫描电子显微镜照片[32-33]Fig.5 SEM micrographs of shark skin samples: a) actual shark skin; b) replica shark skin[32-33]
为了比较各种肋条设计以及肋条结构与流体的相互作用,研究人员通常使用无量纲的肋条间距s+和肋条高度h+来描述,其定义为:

2.2 沟槽表面减阻机理研究
顺流向沟槽表面的湍流减阻机理主要有“第二涡群”理论[13]和“突出高度”理论[36-37]。如图6 所示,“第二涡群”理论认为肋条尖峰与逆转的流向涡相互作用,在肋谷里产生二次涡流,使低速流体保留在肋谷内。二次涡的加速发展可使肋谷内产生离散涡流并迅速消散,从而减弱了流向涡,限制了低动量流体集中。这使得动量交换过程受到抑制,减小了表面剪切应力。另外,二次涡可充当一个反馈机构,减弱了流向涡旋并持续产生二次涡,增加的二次涡显著抑制了低速流体的横向集中和向上提升,从而大大减小了低速条带的数量,使得低速区与高速区的速度差变小。这一过程进一步降低了湍流边界层的不稳定性并且使湍流猝发强度降低,阻碍湍流边界层的发展,从而减少阻力。如图7 所示,“突出高度”理论引入了表观起点(即平均起点)和突出高度(槽峰到表观起点所在平面的距离)的概念,突出高度决定了肋条可影响的流体流动范围。该理论认为由于黏性力的主导作用,表观起点以下凹槽内的流动被阻滞,这相当于增加了黏性底层的厚度,减小了壁面上的平均速度梯度,从而降低表面摩擦阻力。
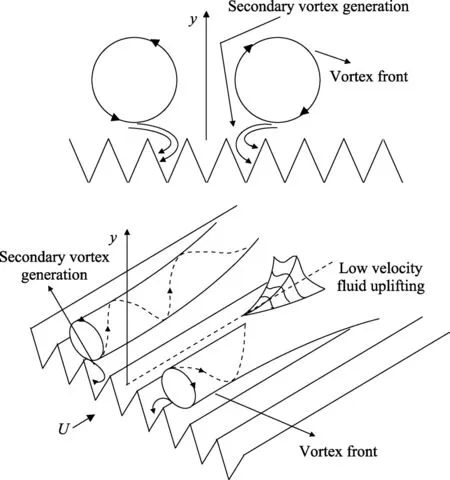
图6 “第二涡群”理论示意图[13]Fig.6 Schematic of “secondary vortex drag reduction”[13]
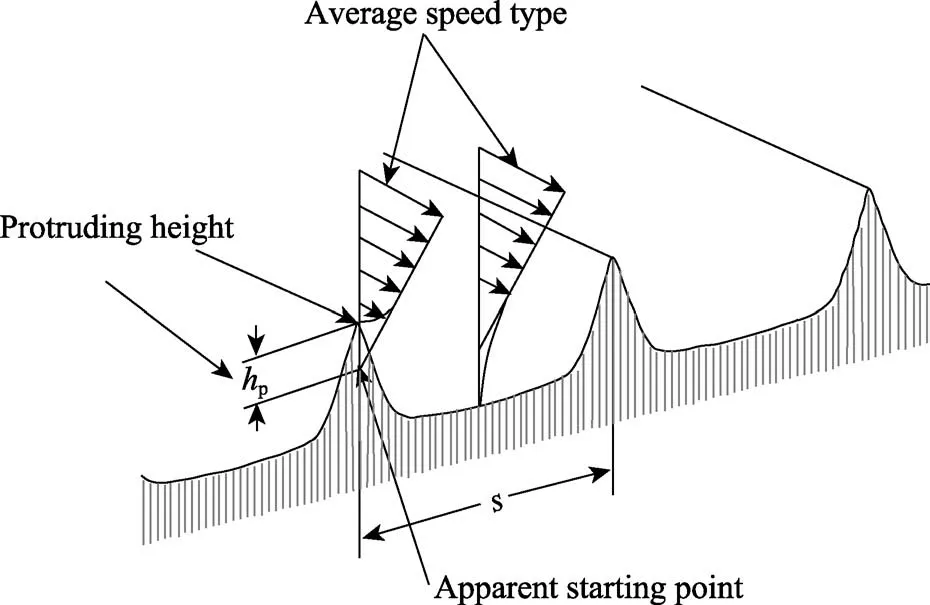
图7 “突出高度”理论示意图[37]Fig.7 “Apparent origin of a riblet surface”[37]
2.3 沟槽几何参数和截面形状对减阻的影响
20 世纪70 年代NASA 兰利研究中心发现沟槽表面能有效地降低壁面摩擦阻力,这彻底改变了之前研究者们普遍认为表面越光滑摩擦阻力越小的传统观点。Walsh 等[19,38-41]最初在平板上对不同沟槽结构的湍流减阻进行了试验研究。如图8 所示,考察了不同沟槽截面类型(对应参数见表1)对减阻行为的影响。结果显示,当对称的沟槽高度和间距满足s+≤ 30 和h+≤ 15 时,沟槽表面具有减阻特性,并指出s+= 30、h+= 15 时可达7%~8%的最佳减阻率。
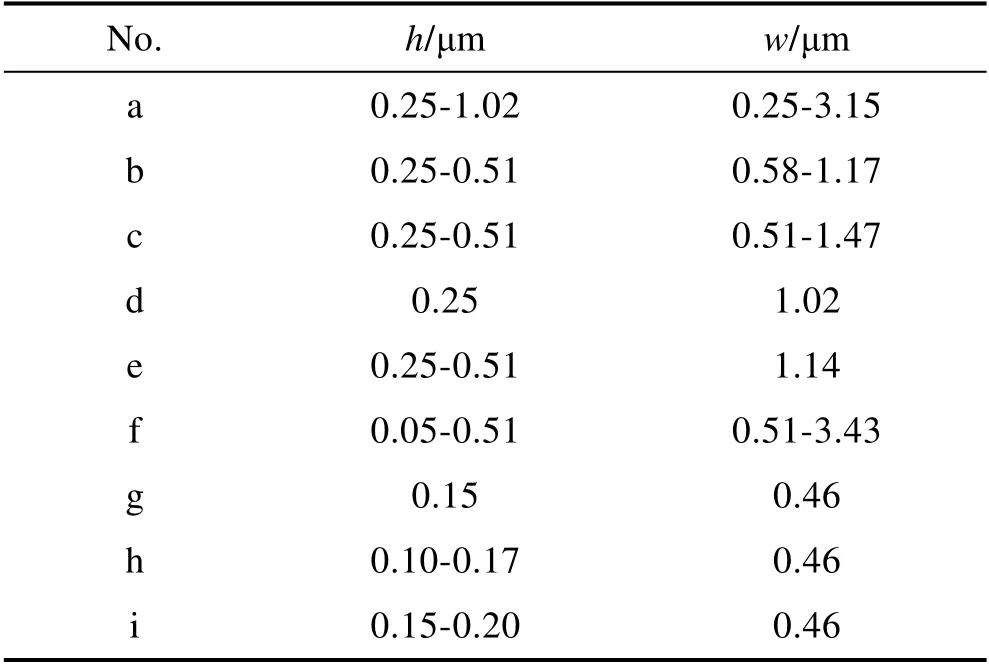
表1 不同类型沟槽的高度和间距Tab.1 Structural height and spacing of different kind of riblets
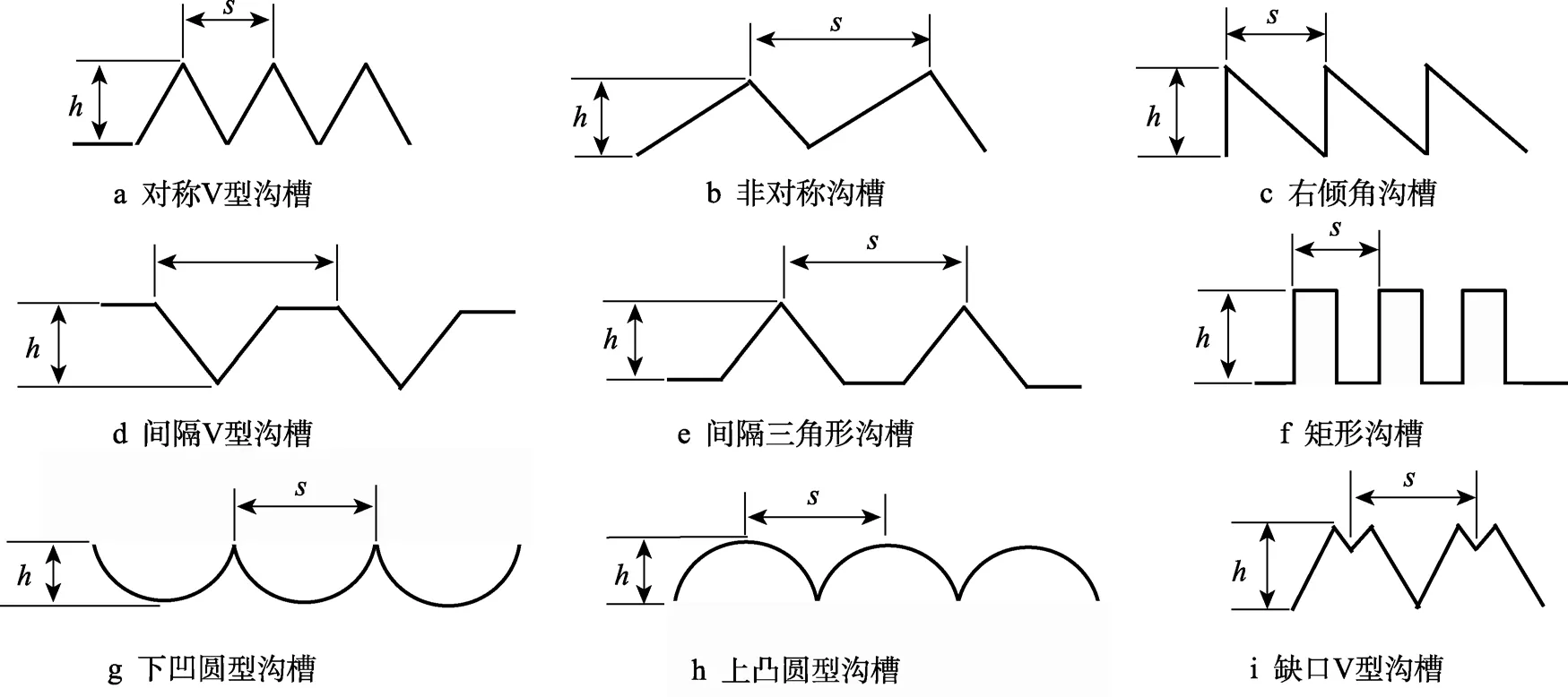
图8 NASA 兰利中心的试验沟槽类型[19]Fig.8 Surface configurations tested by NASA Langley Research Centre[19]
之后研究者们对无量纲沟槽高度和深度与减阻效果之间的关系进行了大量研究。Reidy 等[42]在s+=h+=13.1 的沟槽表面得到了(8.1±2.5)%的减阻效果。Rohr 等[43]研究了h+对减阻效果的影响,当h+=3 时开始出现减阻效果,接近12 时达到6%~9%的最佳减阻效果,而当h+为20~30 时,减阻效果趋近于0。相应地,Baron 等[44]在肋条间距s+为10~15 时,获得了最佳的减阻效果。El-Samni 等[45]认为当s+> 30 时会导致阻力增加。Djenidi 等[46]发现当s+小于或接近25 时出现减阻效果,当s+接近75 时出现增阻。
在截面形状对减阻影响的研究中,Martin 等[31]发现相较于锯齿状和扇贝状的肋条,刀片状肋条的减阻效果最好,最大减阻率可达到11.6%。Arndt 等[47]的风洞试验表明肋条高度为100 µm 的V 型沟槽表面可获得6%的最佳减阻效果。Monfared 等[48]的拖拽水槽试验表明刀片型肋条模型表面具有7%的减阻效果。刘志华等[49]的数值模拟表明V 型沟槽峰的圆角半径越小(峰越尖锐),减阻效果越好。封贝贝等[50-51]对不同沟槽姿态倾角(如图9 所示,β为沟槽顶角α平分线与垂直方向的夹角)模拟后发现β对压力分布有着显著影响,当β为0°时,沟槽面上高压区(迎风面)与低压区(背风面)的压差阻力最小。
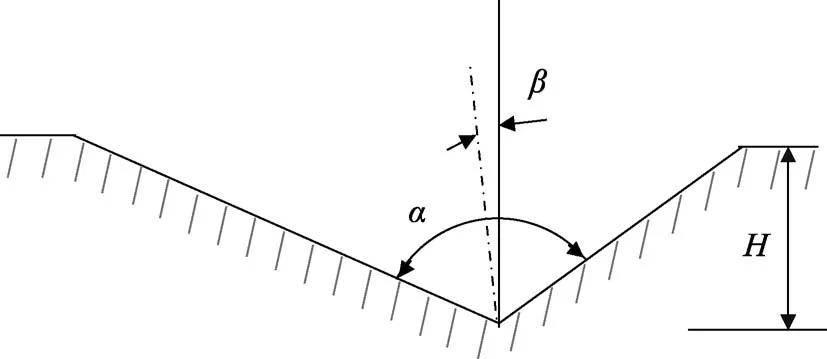
图9 沟槽姿态倾角示意图[50]Fig.9 Sketch of riblet attitude angle structure[50]

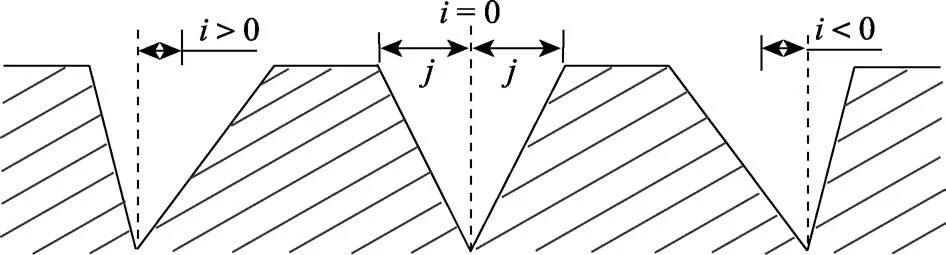
图10 沟槽截面不对称系数示意图[52]Fig.10 asymmetry coefficients and shapes of the micro-grooves[52]
Martin 等[53]深入研究了无量纲参数对流动结构的影响。研究表明沟槽表面附近的涡结构尺寸高度均处于25~30 个无量纲单位,直径为30 个无量纲单位[31],指出沟槽的存在使涡旋提升,远离表面,获得减阻效果。图11a 是表面产生的涡的各种结构参数。平板表面产生的涡会靠近表面并产生大的阻力(如图11b 所示),而在平板上布置适当间距的沟槽后,产生的涡会被抬升而远离表面,减小表面阻力(如图11c 所示)。另外,涡提升距离会随着s+的增大而越来越接近沟槽表面,过大的s+不能提升涡,如图11d 和图12 所示。
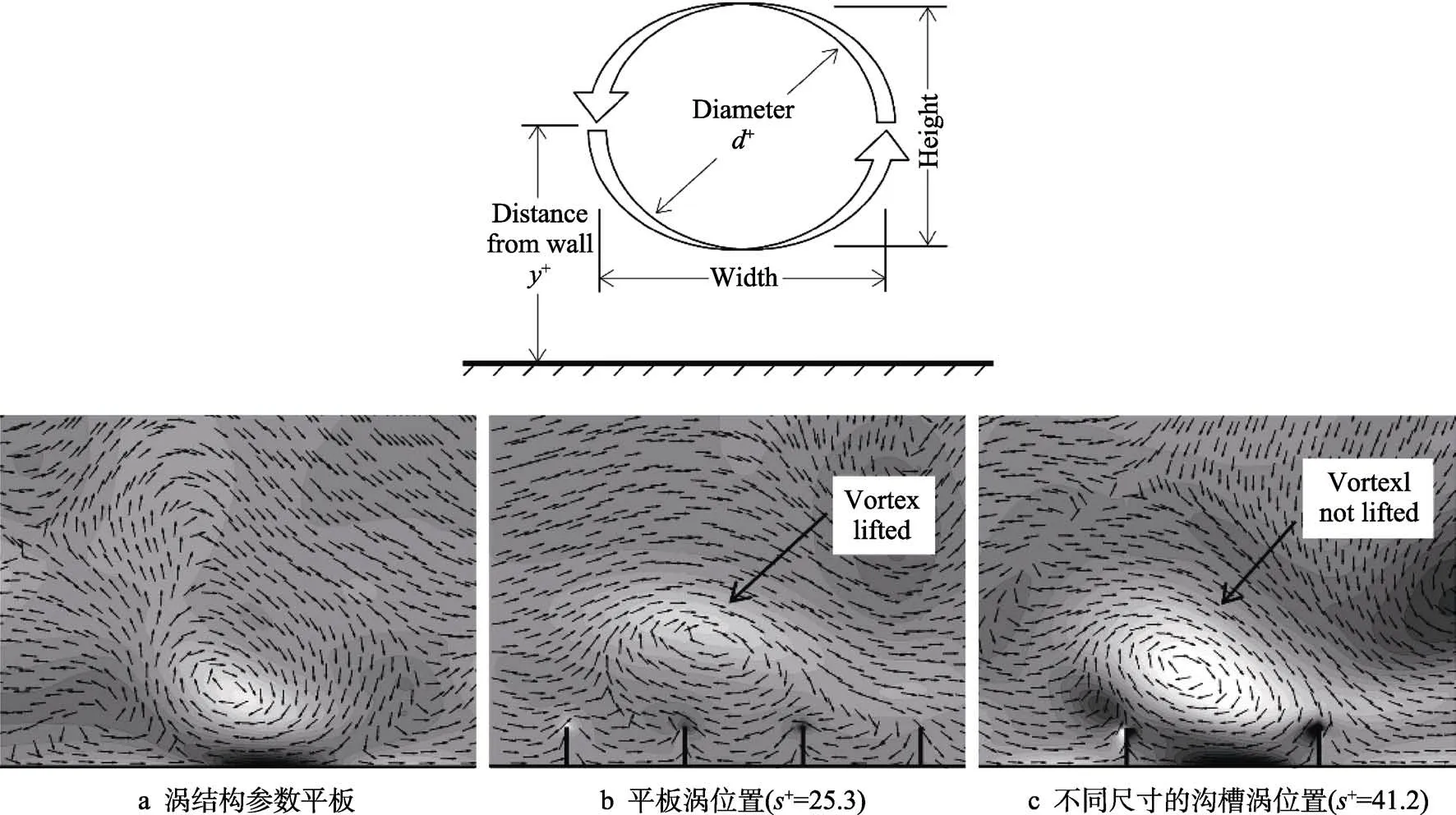
图11 涡结构参数及位置变化[53]Fig.11 Vortex schematic and position changes[53]: a) vortex structure parameters;b) flat vortex position; c) groove vortex positions of different sizes
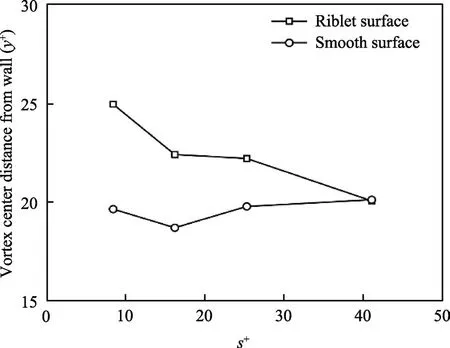
图12 涡中心到壁面距离随s+的变化[53]Fig.12 Vortex center distance from wall for the varying s+[53]
胡海豹等[54]和刘占一等[55-56]从另外的角度解释了沟槽表面间距对减阻效果影响的原因:一方面合适参数的沟槽表面能够抑制压差阻力的产生,另一方面流向涡会改变近壁面流场结构,导致边界层近壁区雷诺应力和壁面剪应力的变化。
2.4 沟槽的排布形式和覆盖率对减阻的影响
Bechert 等[57]的研究表明连续排布的沟槽表面相较于分段排布的沟槽表面能提高2%的减阻性能。Martin 等[53]的研究则显示这一表面的减阻性能提高了5%。然而,Bixler 等[16]指出真实的白斑角鲨鱼皮盾鳞的排布方式更接近于扇贝型。如图13 所示,是一种交错排布,平板试验结果显示,该表面的减阻效果要优于连续排布的刀片型肋条。在此基础上,秦立果等[58]以单个盾鳞的简化模型为单元,对间断排布的沟槽表面进行数值模拟,获得了13%~18%的减阻率。
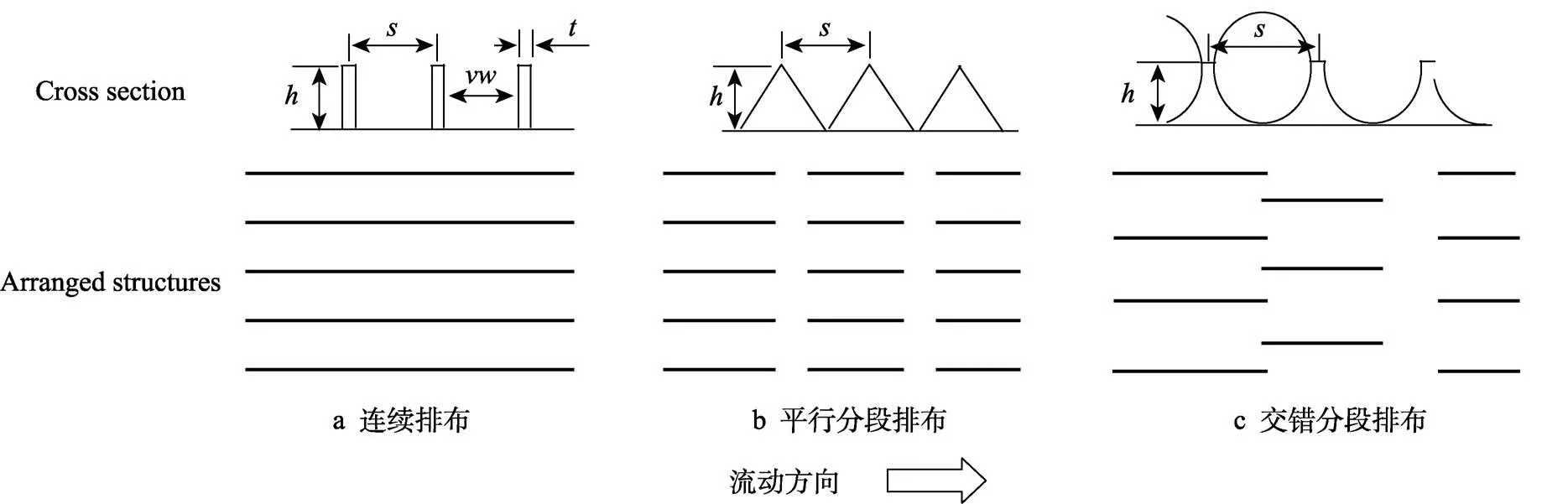
图13 连续、平行分段和交错分段沟槽排布形式[16]Fig.13 Contious (a), aligned segmented (b), and staggered segmented (c) configurations[16]
沟槽覆盖率也影响着表面的减阻行为。Szodruch等[59]对空客A320 试验机进行了壁面摩擦阻力检测,结果显示,有肋条结构薄膜的贴附率约为70%时,实现了其总体阻力约2%的降低。李育斌等[60]在1∶12的运七飞机模型机翼上的部分表面黏贴了沟槽薄膜,风洞试验结果显示该表面可减少5%~8%的阻力。Fu等[61]认为在海洋减阻的应用中沟槽覆盖面积是影响减阻效果的一个重要原因,指出沟槽中的低速流体降低了沟槽表面的平均速度梯度,存在合适的覆盖率区间可使沟槽表面的平均速度梯度达到最佳,阻力更小。
2.5 流动状态对减阻的影响
大量的研究表明沟槽表面减阻效果主要依赖于沟槽的形状、尺寸及其在边界层中的位置,而雷诺数(Re)、马赫数(Ma)等流体运动状态参数对减阻的影响不大,如Walsh 认为主流雷诺数对沟槽表面减阻效果的影响不大[40],Squire 等[62]的试验表明在亚音速和跨音速下Ma对沟槽表面的减阻没有显著影响。但也有部分研究表明特定流动条件下能提升相应沟槽表面的减阻效果,如Gaudet[63]的试验表明选取合适的马赫数可提升沟槽面的摩擦减阻效果。Lee 等[20]对贴有V 型肋条膜的机翼进行了试验研究,在Re=1.54×104的条件下可以获得大约6.6%的减阻率,但在Re= 4.62×104时却增阻9.8%。李恩田[64]的数值模拟研究也表明不同的沟槽尺寸对应着不同的最佳流速范围,使其具有较好的减阻效果。
此外,Boomsma 等[65]的数值模拟表明,在较小逆压梯度下肋条的减阻能力较低。王晋军等[66-68]的研究表明,相较于光滑表面,沟槽面能使转捩为湍流时的雷诺数增大约4 倍,从而大大地降低了平板边界层的阻力。
3 凹坑减阻
3.1 旋成体凹坑表面的减阻研究
相较于沟槽表面,凹坑表面的减阻研究相对较少,但由于凹坑结构更简单且尺寸相对较大,加工成形上具有一定优越性,因此凹坑表面的减阻研究也取得了一定进展。Bearman 等[69]在低速风洞中研究了表面具有圆形凹坑的圆柱体的阻力性能。其设计凹坑深度与圆柱体直径之比为9.1×103,在低Re数下,附有圆形凹坑的柱面具有更低的阻力系数CD,并指出圆形凹坑表面使流动临界状态的雷诺数更低,其对流体绕柱流动的影响与高尔夫球的凹坑表面相似。Choi等[70]对麻面高尔夫球模型进行了减阻机理研究,试验结果显示,非光滑球体比光滑球体的表面阻力系数低50%以上,并在一定雷诺数范围内保持稳定,指出这与凹坑的深度、面积和形状相关;另外对凹坑表面的湍流增强与流动分离的推迟做出了解释。
如图14a 所示,凹坑的存在会在流向上造成流动的局部分离,引发剪切层的不稳定性,产生较大的湍流强度;由于湍流增强,当近壁面的流动重新回到下游表面时会具有较大的动量,能够克服较强的逆压梯度,推迟主分离,减小阻力。此外,如图14b 所示,流动首先在凹坑Ⅰ处发生分离,最后一次分离和再附着发生在凹坑Ⅳ处。Re为(0.5~2)×105时,随着雷诺数的增大过渡点(流动从不稳定的剪切层获得能量的位置)会前移,而流动的重新吸附总出现在同一位置(凹坑Ⅳ处),使得流动的主分离角恒定,从而维持几乎不变的低阻力系数。
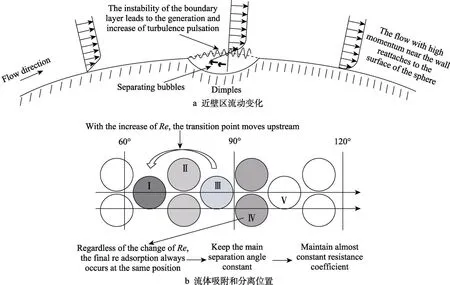
图14 球体凹坑表面减阻机理示意图[70]Fig.14 Schematic diagram of drag-reduction mechanism by dimples on the surface of the sphere[70]:a) flow changes near the wall; b) fluid adsorption and separation position
3.2 平板凹坑表面的减阻研究
虽然一些早期的研究表明凹坑表面对传热有显著提升,但湍流减阻效果并不明显,甚至增阻。Mitsudharmadi 等[18]研究了平板上浅圆形凹坑(截面如图15 所示)表面对边界层发展的影响,当凹坑的深径比为4%、8%和12%时,凹坑仅影响其周围附近的边界层。试验测量观察到在凹坑下游有高速流动的区域,仅出现在凹坑下游1.25D以内,在凹坑上游区域中出现高剪切应力区域,紧邻凹坑中心线下游的平均剪切应力比平板增加了约45%,但在凹坑两侧,平均剪切应力与平板上的湍流相当。并观察到较深的圆角浅圆形凹坑上的流动结构与尖角边缘凹坑产生的流动结构相似。Lienhart 等[24]对大间距、规则排布的凹坑表面进行了试验和直接数值模拟,结果显示,虽然壁面的剪切应力降低,但又有新出现的压力补偿了这一影响,故凹坑表面并无减阻效果。
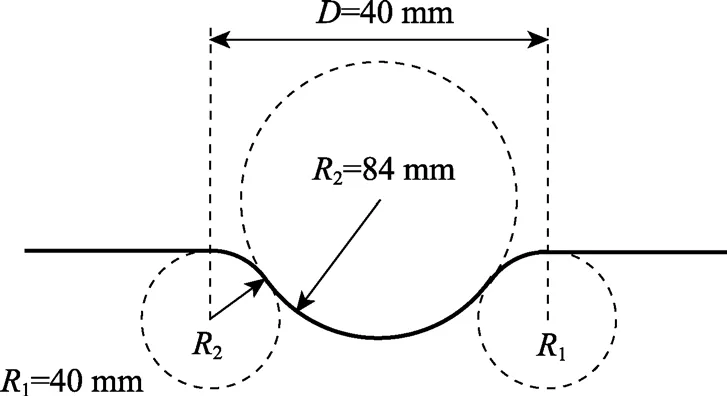
图15 浅圆形凹坑截面示意图[18]Fig.15 Cross-sectional geometry of a rounded spherical dimple[18]
尽管这些研究都发现了凹坑表面的增阻现象,但仍有迹象表明可以通过设计凹坑的几何形状和排布方式来获得湍流边界层的黏性减阻。Veldhuis 等[71]对凹坑表面的减阻能力进行了试验和数值模拟。如图16 所示,设计了4 种凹坑深度和2 种排布形式,大涡模拟表明所有的情况均出现增阻,较浅的凹坑表面摩擦阻力和压差阻力均增加;而较深的凹坑表面摩擦阻力为负,但压差阻力的增大导致总阻力增大。然而风洞试验却得到了相反的结果,在流速为18 m/s、凹坑深度h=0.5 mm 时,排列2 表面可获得21%的最大减阻率,并发现浅圆凹坑在所测的速度条件下均获得减阻效果。另外,较深的凹坑出现增阻,中等深度凹坑在低速条件下出现减阻效果。
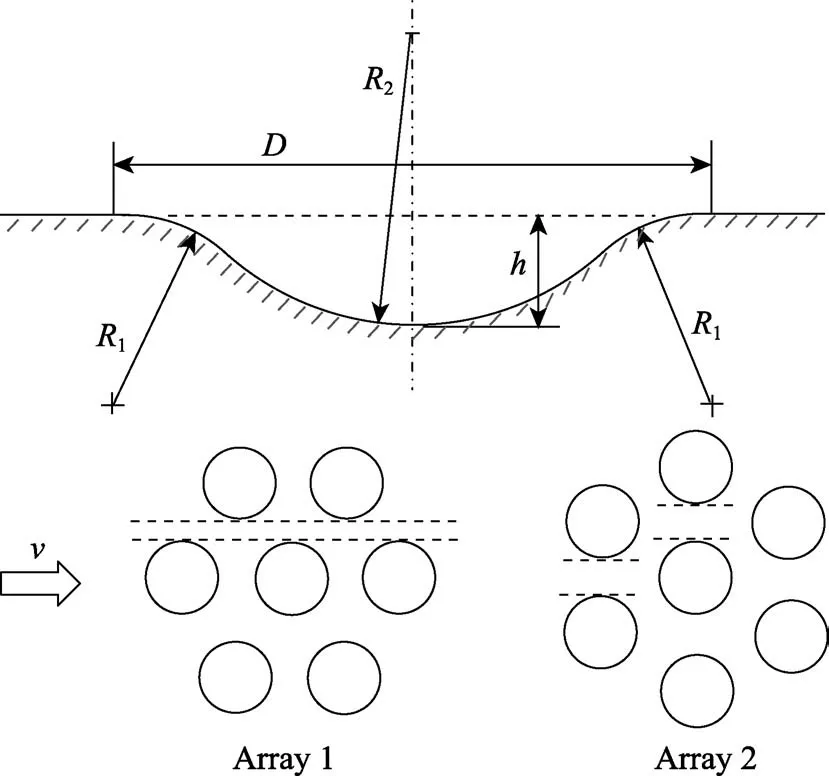
图16 凹坑的几何参数和排布形式[71]Fig.16 Main geometrical parameters of the dimple and dimple patterns[71]
Chear 等[72]采用k-ω湍流模型对具有凹坑表面的汽车模型的空气动力学性能进行了数值模拟,结果显示,凹坑在深径比为0.4 时可获得1.95%的最佳减阻效果。此外,有学者指出在低雷诺数条件下,覆盖率超过70%的凹坑表面才能实现减阻。
国内对凹坑表面减阻性能及其应用的研究多集中于数值模拟。徐中等[73-74]的仿真结果显示,凹坑使表面压差阻力略微上升,却大大降低了摩擦阻力,由此可使总阻力降低,最大减阻率达7.2%;并发现凹坑的底部流体出现逆向流动,指出逆向涡流相当于微滚动轴承,使流过的流体受到滚动摩擦的作用,降低了摩擦阻力。彭世冲等[75]对二维凹坑表面上的流动进行了数值仿真,发现当速度为6 m/s 时,凹坑表面总减阻量最大可达到18.84%,黏性摩擦阻力减阻量达到19.98%,指出凹坑结构能产生影响边界层的流动漩涡,减小了凹坑面附近的速度梯度,从而使表面摩擦阻力减小。在高速列车和汽车表面的空气动力学研究中,数值模拟结果显示,布置凹坑结构的车身表面可获得较好的减阻效果[76-78]。
3.3 凹坑表面的减阻机理研究
在减阻机理研究中,Tay 等[79-80]认为是凹坑引入了流向涡导致流动产生横向速度,加大了湍流能量的耗散使流动更稳定,产生了减阻效果;然而流向涡也会导致流动分离,因此总阻力的降低与否取决于流向涡产生的减阻效果和流动分离区域产生的增阻效果的相对大小。Nesselrooij 等[81]的研究也支持了这一观点。Prab 等[82]在雷诺数为5 830 和11 650 时对凹坑表面进行了稳态的RANS 数值模拟,结果显示,当深径比小于8%时有减阻效果,在深径比为4%~5%时可达3%~4%的最佳减阻率;他们的研究证实了减阻的原因是横向流动抑制了流动分离,这也在很大程度上支持了Tay 的减阻机理。Kiknadze 等[83]提出在凹坑中形成的涡流是减少阻力的关键机制,指出这些旋涡可以充当流体的“滚珠轴承”,并且在反向流动的区域中会引起正剪切力。然而Campenhout 等[21]认为凹坑的减阻机理与涡的产生无关,主要是因为凹坑与流体的相互作用导致近壁面流动出现垂直于流向的交替激励,并与湍流的相干结构相互作用,降低了发夹涡强度,导致减阻。
3.4 凹坑表面的流动结构研究
Ligrani等[84]和Mahmood 等[85]研究了流体流过圆形凹坑表面时的流动结构,对凹坑深径比为1 的流动可视化图像进行了细致分析,发现凹坑中有周期性涡脱落的流动特征。如图17 所示,在t=0 s 和t=0.017 s时,二次流平流进入凹坑并形成成对的回流区;随着流动的发展(t=0.033 s 和t=0.050 s),凹坑中的流体以较强的流动强度从两侧向上突射形成上冲区,回流区的流体在上冲区发展为蘑菇形的逆向涡对,随后初级涡对被拉伸得更长更窄,随流动向下游平移。最后(t=0.067 s 和t=0.083 s),随着新流体的流入,该突射和脱落过程又回到初始状态。
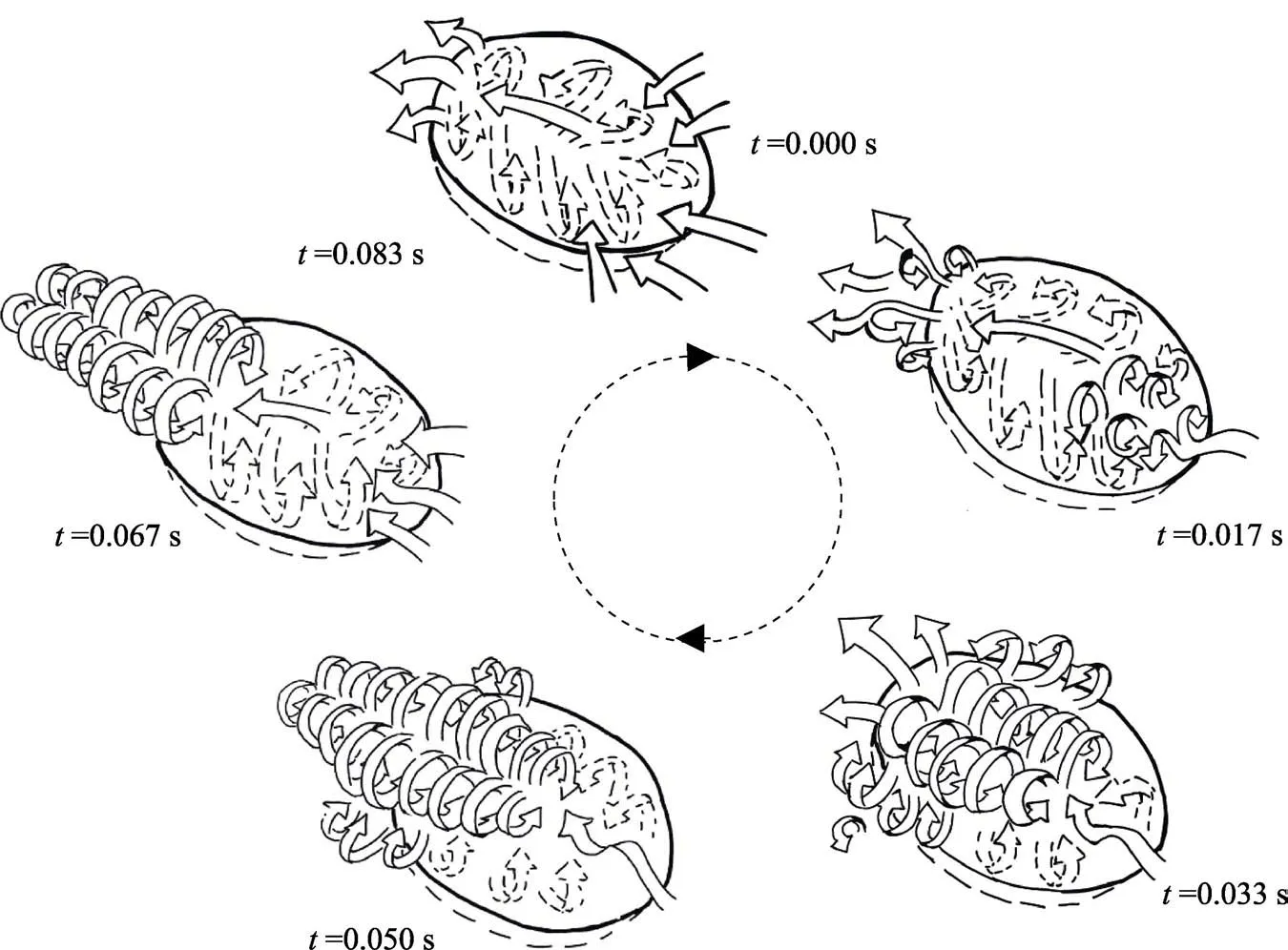
图17 周期性涡脱落流动特征示意图[66](实线表示凹坑上方或外侧的二次流动,虚线表示凹坑内部的二次流动)[84]Fig.17 Sketches of instantaneous, three-dimensional flow structure determined from flow visualization images (solid line arrows denote secondary flows above and outside of the dimple, dashed line arrows denote secondary flows within the dimple)[84]
Won 等[86]研究了凹坑深度对流动结构的影响。流动可视化结果显示,每个凹坑都周期性地突射出初级涡流对,并且该涡对与沿着凹坑的横向边缘形成的边缘涡流对一起存在,边缘涡对表现出不稳定的波动,并且随着凹坑深度的增加,流体突射越强。此外,近壁面压力、横向速度及纵向涡等明显的流动结构会随着凹坑结构的直径、深度和排列密度发生明显变化[87-88]。
4 自适应表面减阻
根据生物力学计算,海豚的最高游泳速度不超过20 km/h,然而在水中的实际游动速度可达40 km/h,若以此速度运动其所受的阻力将远远超过自身肌肉强度[89]。因此,海豚实际受到的阻力应远小于此速度运动时其所受的名义阻力,而这一奥秘在于海豚能有效控制所受阻力。早在1936 年,Gray[90]发现海豚在水中以惊人的高速运动时鱼体的后部会在竖直平面上有节奏地振动,并且尾鳍的形貌会随运动速度而改变,加速鱼体后部周围的流体,阻碍流经体表的流体发展为湍流。
4.1 自适应表面理论模型
流体驱动与自适应表面响应运动的理论模型可以分为压力驱动和压力、壁面剪切力共同驱动2 种类型[91]。Duncan[92]和Kireiko[93]主要关注了流体对自适应表面的压力驱动和自适应表面的垂直位移响应,建立了弹簧阻尼支撑板的自适应表面模型,如图18a 所示。为了考虑负雷诺应力对湍流和流动稳定性的影响,Carpenter 等[94-95]建立了各向异性的自适应表面模型,如图18b 所示。该模型是一个支撑在倾斜的弹簧杠杆臂上的薄板,在波动压力的作用下表面会同时产生水平位移和垂直位移,并具有简单的线性相关,这样就考虑了自适应表面对流体剪切的响应。
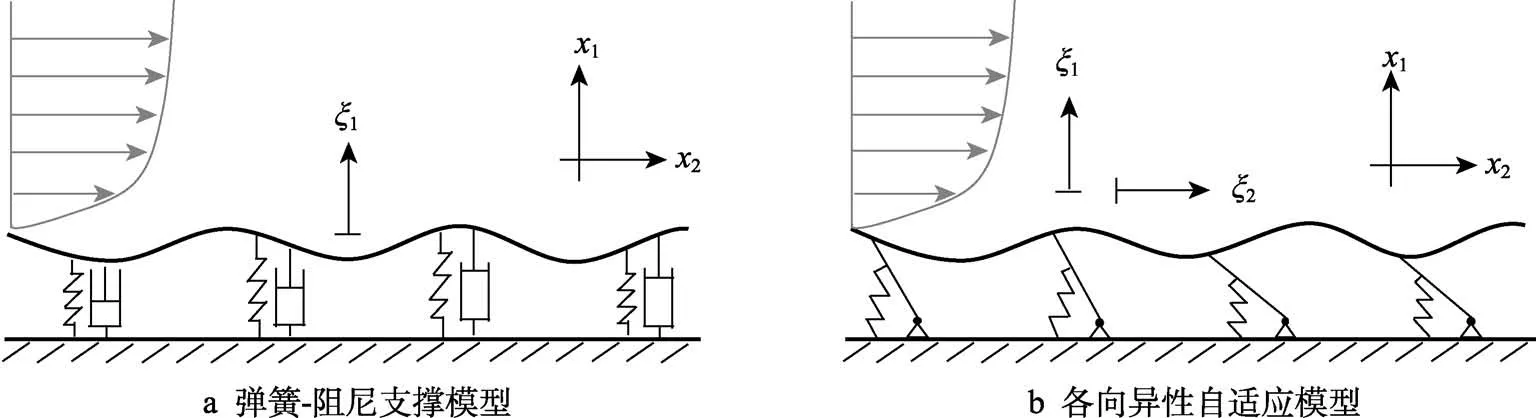
图18 自适应表面模型[91]Fig.18 Compliant wall models[91]: a) spring and damper supported model;b) pressure- and wall-shear-stress-driven anisotropic
4.2 自适应表面减阻机理研究
Kramer[96]最初对仿生海豚体表的自适应涂层(见图19)的试验研究获得了减阻效果。试验表明,相较于刚性表面上的迅速转捩,自适应表面能够使受到扰动的流动恢复完全层流状态,具有极好的层流保持性。并将减阻归因于自适应表面可以稳定边界层流动,推迟边界层转捩,使自适应表面上的流动长时间保持层流,从而减小受到的阻力。
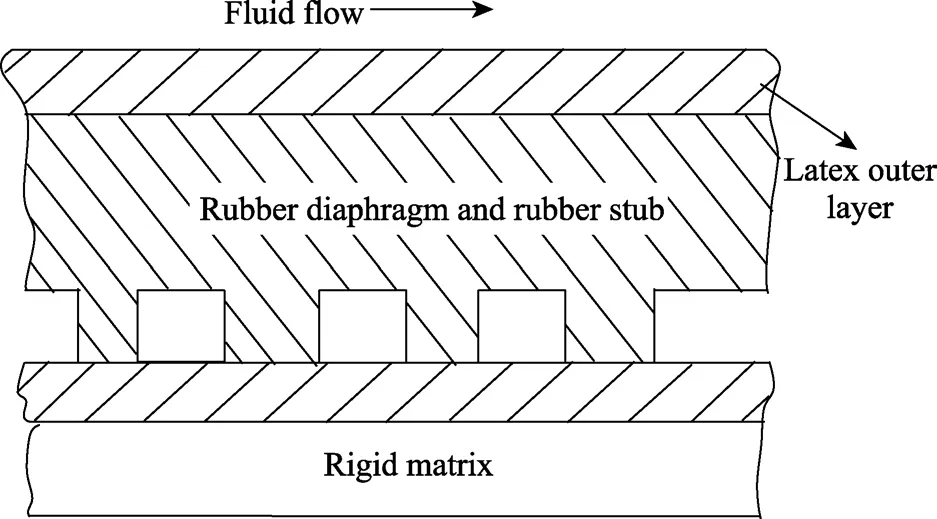
图19 Kramer 自适应涂层横截面示意图[96]Fig.19 Schematic of compliant cross section of Kramer[96]
根据边界层线性稳定理论(LST),自适应表面能够减弱Tollmien-Schlichting 波(TSW)在边界层内的增长速率使边界层转捩推迟[94,97-99]。如图20 所示,Gaster 等[100]用输出(热膜测量值)与输入(TS 波发生孔)的压力振幅比随着流体速度的变化来表征扰动增长,比较平板与自适应表面,发现平板上发生转捩是在流体速度为2.7 m/s 时。而在自适应表面压力振幅比会突然增大,转捩推迟出现在2.77 m/s 和2.78 m/s 处,并且自适应表面上TSW 的增长率明显低于刚性表面。
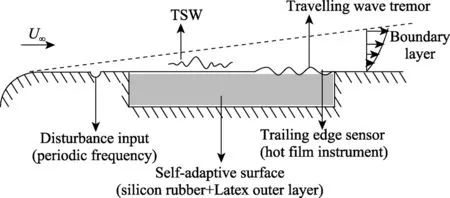
图20 Gaster 等人试验原理图[100]Fig.20 Schematic of the experimental setup of Gaster, et al[100]
Lee 等[101]的水槽试验进一步证实了自适应表面能够抑制湍流的发生。试验比较了刚性表面和单层黏弹性自适应表面上的湍流边界层结构,发现自适应表面上湍流动能和雷诺应力都减小,指出这是由于近壁区域低速条纹带横向距离增加和对数律层的上抬造成的。Lucey 等[102]应用Gaster 的试验发展了自适应表面的边界层理论,指出了行波震颤(TWF)对流体流动的影响,TWF 是表面所引起的行波,会随流体对壁面传递的能量逐渐增大。试验和理论计算都表明在自适应表面上边界层转捩是具有选择性的,如果要实现减阻或转捩延迟,需要尽量避免TWS 出现。Tsigklifis 等[103]的研究也表明边界层的转捩会通过旁路路线迅速猝发。
4.3 自适应表面湍流减阻研究
Choi 等[104]对自适应表面在湍流边界层中的减阻进行了试验研究,结果显示,减阻率可达到7%,湍流强度几乎在自适应表面的整个边界层内减小了5%,同时观测到了对数律层的上抬,意味着黏性子层增厚,湍流阻力减小。并基于半经验理论模型指出自适应表面能够实现湍流减阻必须满足:(1)表面变形位移小于黏性子层厚度;(2)表面的固有频率和湍流猝发的固有频率应接近。
自适应表面湍流减阻研究大量地应用了数值模拟方法。Endo 等[105]利用DNS 对各向同性材料的自适应表面模型进行了湍流模拟获得2.7%的减阻率。但Xu 等[106]的数值模拟表明,在长时间的湍流流动下,自适应壁面阻力和近壁湍流统计量的变化都比较小。Fujimatsu 等[89]采用了较为简单的壁面运动方程,模拟获得了5.6%的减阻效果,指出壁面运动能有效减少湍流涡度和湍流摩擦阻力。Fukagata 等[107]对各向异性材料的自适应表面模型进行了湍流模拟,结果显示,各向异性自适应表面上的雷诺应力为负值,通过调整材料的特性参数在低雷诺数条件下可达到8%的减阻效果。Xia 等[108-109]通过对瞬时流场的观察发现各向同性自适应壁面波动振幅的增大会对湍流统计量产生巨大影响,不过壁面摩擦阻力系数Cf总是增大的。另外不同于各向同性的自适应表面,各向异性自适应表面引入的雷诺应力会导致Cf产生新的一项Cw,补偿了由于雷诺应力减小对Cf的减小作用。他们指出雷诺应力的减小导致阻力减小的自适应表面直观减阻机理是不适应其研究结果的。
5 结论与展望
本文对沟槽、凹坑和自适应3 种类型非光滑表面在减阻方面的研究进行了细致论述。就减阻效果而言,沟槽表面的湍流流动一般可以达到10%左右的减阻率;凹坑表面的湍流减阻受流动条件、几何参数和排布的影响剧烈,特定条件下可以实现表面减阻,最大减阻率可达20%;自适应表面的减阻主要是通过提高转捩雷诺数和延缓湍流猝发来实现减阻[110-111],其在湍流流动下的减阻率一般为10%左右。另一方面,在机翼、汽车车身、船体和管道等的应用研究中,理论计算的减阻率一般是小于试验研究的。非光滑表面减阻机理的研究中,沟槽表面已具备较为成熟的湍流减阻理论,而由于缺乏边界层流体黏性子层结构的详细数据,并且表面对黏性子层结构的影响不明晰,凹坑表面和自适应表面的湍流减阻机制仍存在较大争议。
表面减阻可通过多种方式实现,但从应用前景和技术等方面考虑,非光滑表面具有独特的优势和不可替代的研究价值。近十几年来,非光滑表面减阻是主要的表面改性方法之一,并且已在天然气管道、飞机、航运、泳衣等工程实际中得到了成功使用。在减阻机制上,许多学者也开展了广泛的研究,但仍需砥砺前行[4]:
1)非光滑表面(尤其是凹坑表面)在一定条件下展现出理想的减阻效果,然而流动条件发生改变,减阻效果会减弱或消失,甚至会出现增阻效果。如何扩大非光滑表面的适用范围或者在某一使用条件下(微小变动)使得非光滑表面具有稳定的减阻效果仍旧是一个尚未解决的重要问题。
2)由于非光滑表面结构尺度小,减阻效果容易受物理干扰,因此需要进一步探索如何保护减阻表面免受损坏和污染。例如,如果海洋船体表面被微生物附着,非光滑表面的减阻功能可能会有所降低,甚至消失或变成负作用。建立多学科的交叉理论与技术,实现基于可监测和智能化表面仍任重而道远。
3)大部分试验和理论分析仍处于实验室研究阶段。在特殊工况如海洋极端条件下,研究气固、气液和固液两相接触表面对减阻行为的影响,以及多场耦合下流体的变形与流动机理的揭示,将有助于实现工程表面的运行可靠性和全寿命周期的服役行为。

