析取置信规则库系统参数优化的深度神经网络模型

郑铭鸿，方炜杰,叶己峰，傅仰耿

(福州大学计算机与大数据学院，福建 福州 350108)

0 引言

为更好地解决信息中存在的模糊性、不确定性和不完整性等问题，Yang等[1]在D-S证据理论[2]、模糊理论[3]、决策理论[4]和传统的IF-THEN规则[5]的基础上，提出了基于证据推理的置信规则库推理方法，能够更好地表示与处理不确定性信息.置信规则库(belief rule-base,BRB)系统的前件属性的连接方式主要有合取和析取[6]两种方式，前者被称为CBRB(conjunction belief rule-base,CBRB),后者被称为DBRB(disjunction belief rule-base,DBRB).Chang等[6]对两者进行了充分分析，证明了DBRB系统在具有更小规模的同时也拥有较好的推理精度.

在置信规则库的基础上,Raihan等[7]将深度学习与置信规则库结合(BRB-DL)，使用神经网络计算BRB的规则权重，利用神经网络对信息的记忆性，提高BRB对数据的处理能力.然而，在推理过程中，规则权重、属性权重等系统参数都将直接影响最终的推理结果.目前已有许多学者在BRB的参数优化问题上进行研究，如Chen等[8]使用Matlab工具箱的“fmincon”函数进行参数优化，但是该方法基于Matlab平台实现，算法的可移植性低.Wang等[9]提出使用差分进化算法进行参数优化(differential evolution，DE)，但是DE算法需要额外的大量时间计算寻优，每次的寻优都是通过一定的规则或概率分布逼近最优点，优化效率较低，而BRB-DL由于引入了神经网络增加了系统的参数和规模，将导致DE算法的训练效率进一步降低.Wu等[10]引入梯度下降算法来提高BRB模型的优化速度和收敛精度，但是由于BRB模型本身参数的约束，需要通过设置特定的步长来确保模型参数满足约束条件，从而导致了梯度下降实现困难，优化效率不高.总之，目前针对BRB-DL的参数优化方法或多或少都有其自身的不足.

针对以上问题，本研究首先引入深度神经网络(deep neural network,DNN)与DBRB结合(DBRB-DNN)，DBRB系统的规则构建是通过前件属性的参考值线性组合而成，系统规则数和参数的数量相比CBRB更加精简，系统的复杂度更低.接着，引入梯度下降算法对DBRB-DNN的系统参数进行优化，同时针对DBRB-DNN中因参数约束导致梯度下降算法应用效率低的问题，对DBRB-DNN的系统参数进行预处理，从而使得梯度下降算法更好地应用在DBRB-DNN上.最后，将模型的应用范围扩展到分类问题上，并在分类和回归问题上进行实验，验证本文提出方法的有效性.

1 析取置信规则库(DBRB)系统

1.1 DBRB的规则表示

析取型BRB系统[6]是通过析取符号连接不同的前件属性，其中第k条规则表示为

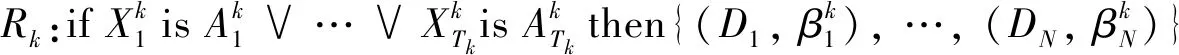
(1)

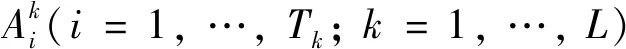
1.2 DBRB-DNN模型

DBRB-DNN系统是对BRB-DL[7]系统的改进.首先，DBRB-DNN使用析取置信规则库与神经网络结合，缩小了系统规模，简化了前件属性权重δ和规则权重θ两个系列的参数.其次，针对BRB-DL因使用“relu”函数导致的神经元坏死，损失值无法下降的问题，DBRB-DNN引入“tanh”函数进行改进.最后，针对BRB-DL只用于解决回归问题的局限性，本文将DBRB-DNN应用在分类问题上，扩展其应用范围.DBRB-DNN模型主要的工作过程如图1所示.

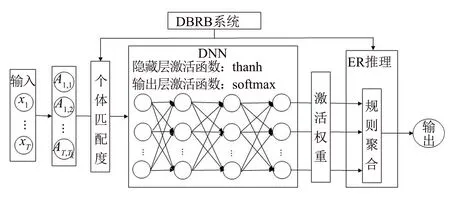
图1 DBRB-DNN工作流程Fig.1 Working process of DBRB-DNN

1.3 DBRB-DNN系统的推理方法

DBRB-DNN推理过程主要分为2个步骤[1]：1) 激活权重计算；2) ER算法合成规则.

1.3.1 激活权重计算

计算激活权重之前，首先要计算输入数据对前件属性参考值之间个体匹配度，一般采用欧式距离进行计算.对于输入数据X的第i个分量xi，可以转化为如下形式.

S(xi)={(Ai,j,αi,j),i=1,2…,T;j=1,2,…,Ji}

(2)

其中:αi,j表示输入xi对于前件属性参考值Ai.j的匹配程度.接下来，使用DNN计算每条规则的激活权重，其中输入层的神经元个数等于前件属性参考值的个数，输出层神经元的个数等于规则的条数，每层神经元之间采用全连接的方式.神经元之间的具体工作方式如下.

zk=ckαk+bk

(3)

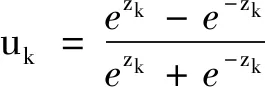
(4)

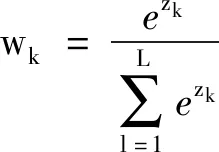
(5)

其中式(3)和(4)为隐藏层神经元工作方式，式(3)和(5)为输出层神经元工作方式;ck表示的是神经元的权重值,为一组矩阵向量；ak表示的是个体匹配度,为一组输入向量；bk表示的是神经元的偏置值；uk表示隐藏层的非线性输出；wk为权重值.

1.3.2 ER算法合成规则

计算出每条规则的激活权重后，用ER合成公式对所有的激活规则进行合成.在规则完整的情况下，输入x，第i个结果评价等级上的置信度βi(x)计算公式[12]为

(6)

其中，

(7)

上述公式合成后,得到结果置信分布{(Dn,βn)|n=1,2,…,N}.对于分类问题，一般直接选取置信度值最大所对应的结果评价等级作为结果输出.对于回归问题，则要使用各个评价等级对应的效用值与其对应的计算得出的置信度进行加权，得到数值型的输出.

2 基于梯度下降的参数优化方法

2.1 DBRB-DNN的偏导数

通过节1.3，可分析得出DBRB-DNN需要优化的参数有神经网络中每个神经元的权重和偏置值以及每条规则的结果置信度,本研究应用梯度下降法[13]训练DBRB-DNN.

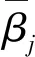
(8)

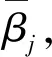
(9)

(10)

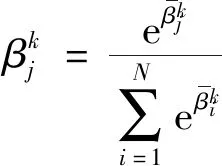
(11)

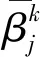
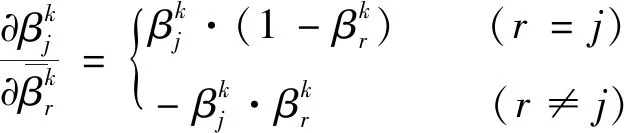
(12)

式(7)中第k条规则的激活权重wk来自于神经网络的输出.本研究选用多层的全连接深度神经网络与DBRB进行结合，当损失值通过反向传播到神经网络后，神经网络将根据损失值计算每一层神经元的权重和偏置的偏导数，根据式(5)可以求得输出层激活权重对线性输出zi的偏导数为

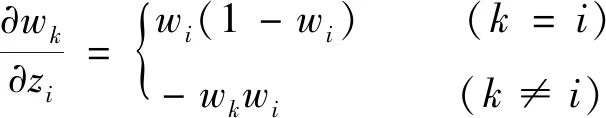
(13)

根据式(4)可以求得神经层内部权重对线性输出zk的偏导数为

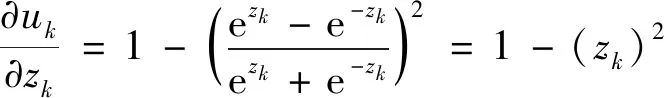
(14)

接着,根据式(3)求得线性输出zk对输出层神经元权重和偏置的偏导数为

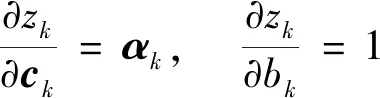
(15)

当求出输出层神经元对应的权重和偏置的导数时，可根据损失值继续反向传播求出神经网络每一层的神经元权重和偏置的偏导数.

得到系统每一步参数的偏导数，根据链式求导法则，可以分别得到损失函数对推理系统第k条规则各参数的偏导数.第k条规则中第j个结果属性的置信度的偏导数为

(16)

这里用C和B表示神经网络中所有的神经元权重和偏置值，神经元的权重和偏置值偏导数为

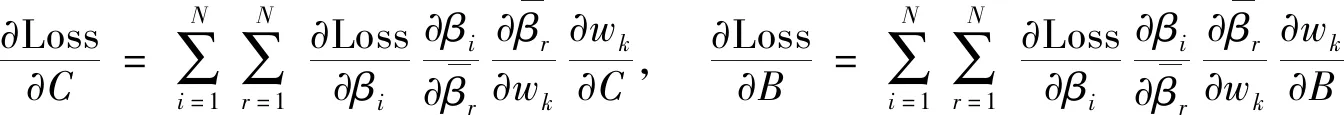
(17)

计算出系统所有待优化参数的偏导数，就可以求得参数优化的方向，使用梯度下降算法训练DBRB-DNN模型.

2.2 优化模型

通过对DBRB-DNN模型的分析，需要优化的参数有

(18)

使用梯度下降进行参数训练的模型可以表示为

Pnew(C,B,β)=Pold(C,B,β)-λ∇Poldloss

(19)

其中，λ表示参数模型沿负梯度方向更新的学习步长.

基于BRB的优化模型[14]，提出DBRB-DNN的优化模型如图2所示.

图2 DBRB-DNN参数优化模型Fig.2 Parameter optimization of DBRB-DNN

DBRB-DNN优化的目标函数为

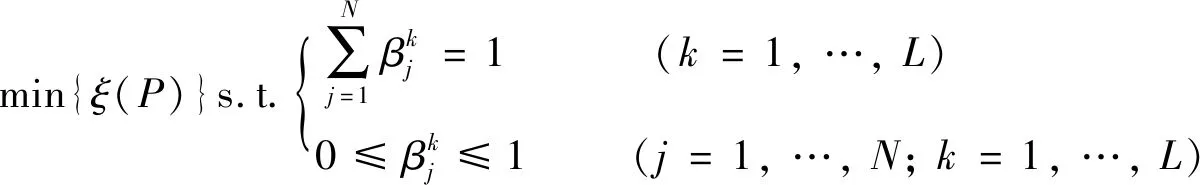
(20)

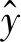
(21)

其中：ui表示第i个结果属性对应的效用值.

(22)

从上述分析可以看出，假设神经网络有K层，输入层有A个神经元，隐藏层的神经元有S个，输出层神经元有L个,DBRB-DNN系统的训练模型包含的训练参数为S1=N×L+S×(K-2)+L+A×S+S×L+(K-3)×S2个，约束条件为S2=N×L+L个，实际上就是一个求解含有S1个参数，且带有S2个约束条件的非线性优化问题.算法步骤如下.

步骤1构造初始DBRB-DNN系统并设置梯度下降的初始参数(如学习率、步长等).

步骤2划分训练集和测试集，并使用训练集正向推理计算出损失值ξ(P).

步骤3计算出DBRB-DNN模型待优化参数的偏导数，并根据损失值反向传播更新待优化参数.

步骤4根据更新得到的参数判断损失值ξ(P)是否减小.如果减小，则更新参数；否则，保留上一代的参数.

步骤5判断是否满足终止条件(如：达到设定的最大迭代次数)，如果满足，跳出训练并保存模型;否则，跳回步骤3.

3 实验部分

本实验选取一个5层的DNN神经网络与DBRB相结合，输入层神经元的个数为前件属性参考值个数，输出层神经元个数为DBRB规则库的规则数.本节首先对多峰非线性函数进行拟合；然后，通过北京市PM2.5的预测实验验证模型的性能；最后，从UCI上选取多个公共数据集进行分类问题上的对比实验.实验环境为：Inter(R) Core(TM) i7-6700 CPU @ 3.40 GHz 3.41 GHz；16 GB内存；Windows 10操作系统；算法实现平台为Visual Studio Code 1.57 x64；Python版本3.8.5.

3.1 多峰函数非线性拟合

在本节中，拟合一个多峰非线性函数，以验证梯度下降算法优化参数的有效性.DBRBD-DNN的神经网络有5层，输入层有5个神经元，输出层有5个神经元，3个隐藏层各有20个神经元.非线性函数公式如下.

g(x)=e-(x-2)2+0.5e-(x+2)2(x∈[-5,5])

(23)

由式(23)分析可知，当变量x取-2,0,2时为多峰函数的极值点，根据极值点可以设置规则结果属性的评价等级和相应的效用值.

{D1,D2,D3,D4,D5}={-0.5,0,0.5,1.0,1.5}

(24)

选择自变量x作为规则的前件属性，选择5个极值点作为前件属性的参考值，分别为{-5,-2,0,2,5}.然后在0和1之间随机初始化结果属性的置信度，同时随机初始化神经网络中的权重值和偏置值.

接着，采用梯度下降算法对初始DBRB-DNN模型进行训练.通过在定义域上对自变量x均匀选择1 000个值作为拟合数据集，学习率设置为0.001，每个批次使用64个样本，训练次数分布设置500,1 000和1 500次进行3次实验.训练后的DBRB-DNN的性能如图3所示.可以看出，经过训练的DBRB-DNN可以很好地拟合函数g(x).

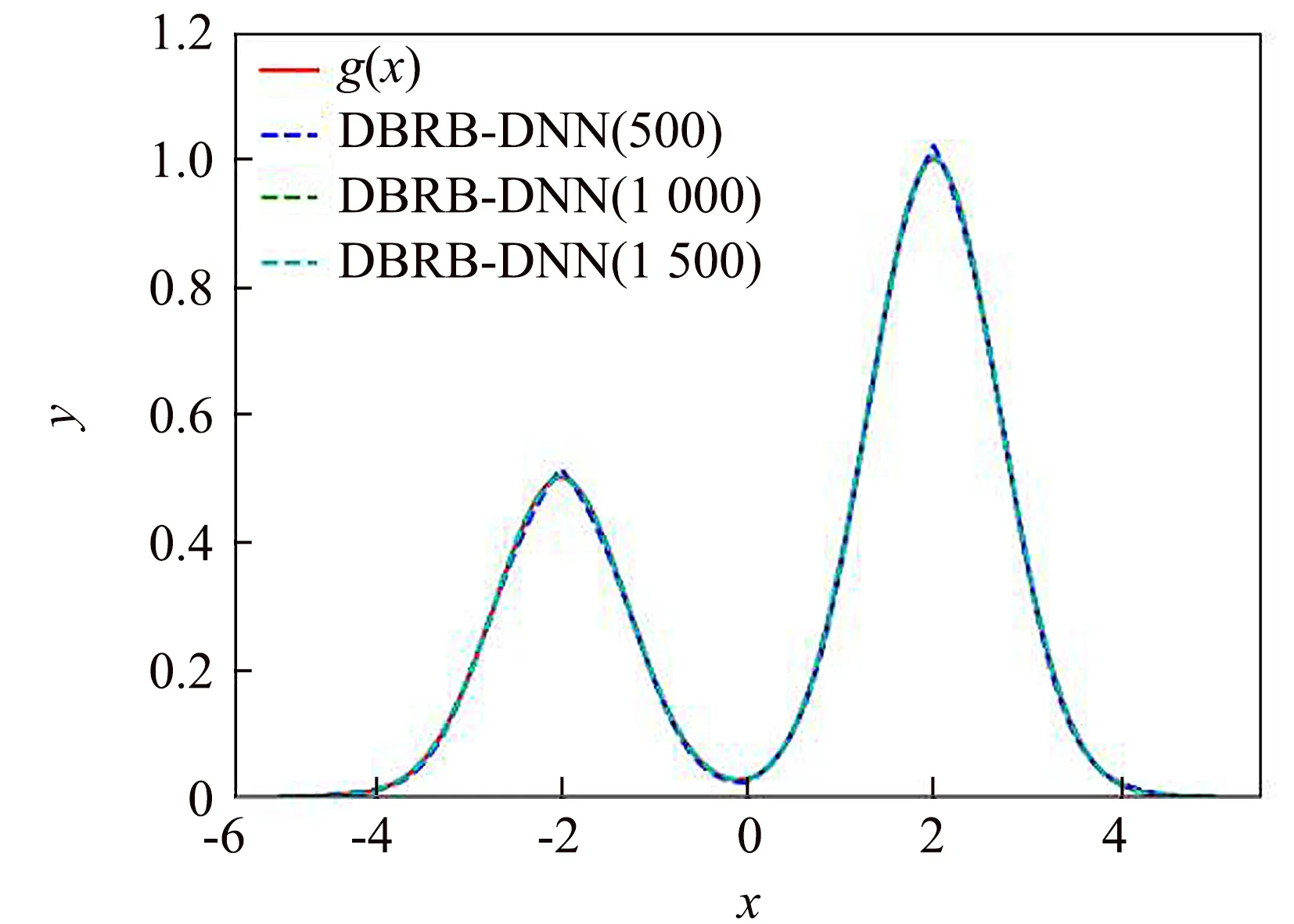
图3 基于梯度下降的DBRB-DNN输出结果Fig.3 Results of DBRB-DNN based on the gradient descent algorithm

为更好地验证本文所提出的基于梯度训练的DBRB-DNN方法，本实验分别与文献[7,9,15]中的方法进行比较，以均方误差(MSE)和运行时间(s)为指标，文献[7]的相关实验在MATLAB R2020b中实现.从表1可以看出，本文所提方法在1 000次迭代训练以后时间和精度上都最佳，而500次迭代训练虽然排名第二，但是在时间上仍远高于其他文献的方法.

表1 函数拟合性能比较Tab.1 Comparison of function fitting performance

3.2 北京市空气质量污染预测

为进一步验证本文提出的DBRB-DNN模型的性能，使用北京市空气质量数据集进行实验，数据集总共含有43 824个样本点.首先对数据集进行归一化处理，接着使用五折交叉验证来评估模型的性能.露水、风向、风速作为前件属性，PM2.5的值作为结果属性.其中每个属性有3个参考值，神经网络有5层，输入层神经元有9个.输出层神经元有3个，3个隐藏层神经元各有12个.学习率为0.001，每个批次使用128个样本，并进行1 500次迭代训练.图4展示了DBRB-DNN在测试集上PM2.5预测值与实际值的对比.其中横坐标为样本点的数量，纵坐标为PM2.5归一化后的预测值.

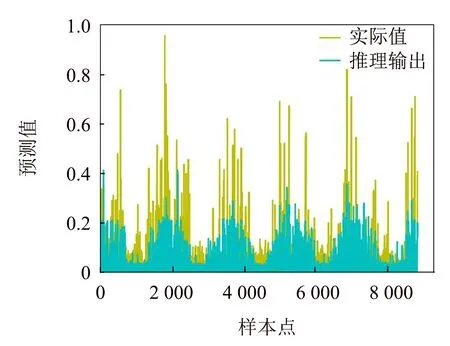
图4 DBRB-DNN对PM2.5的预测值与实际值的比较Fig.4 Comparison of actual PM2.5 values and predicted PM2.5 values by DBRB-DNN

从图4中可以看出，经过训练后的DBRB-DNN模型在测试数据集上具有较好的预测精度.为了更加直观地验证本文模型的性能，接下来还将与文献[7]方法、LSTM神经网络以及DNN神经网络进行比较，其中LSTM和DNN模型的具体参数和设置参考文献[7].取均方误差和运行时间作为评价指标，比较结果列于表2.其中表2中的第一轮到第五轮表示五折交叉验证中每一轮的MSE值，平均表示五折验证以后MSE的平均值，平均运行时间指五折交叉验证每一轮的平均运行时间，文献[7]的运行时间为本文在MATLAB R2020b中实现.

从表2中可以明显地看出，在五折交叉验证中，DBRB-DNN每一轮的MSE值都优于其他几种方法，最终的平均MSE值为0.002 78也是最佳的.这一结果表明，本文所提出的方法优于其他几种模型，而在平均运行时间上，本文所提出的方法为753 s，也远低于文献[7]方法.

表2 不同方法下MSE值比较和平均运行时间Tab.2 Comparison of MSE values under different methods and average running time

3.3 公共分类数据集实验研究

研究选取7组UCI的公共分类数据集来验证本文所提出的方法.实验方法采取十折交叉验证，取平均准确率作为比较指标.DBRB-DNN的属性参考值个数统一设置为5个(即DBRB的规则数为5条)，神经网络有5层，输入层有5n个神经元(n为每个数据集对应的特征数)，输出层有5个神经元，3个隐藏层各有20个神经元，学习率为0.001，每个批次使用128个样本，并进行1 500次迭代训练.7组数据集的详细信息列于表3.

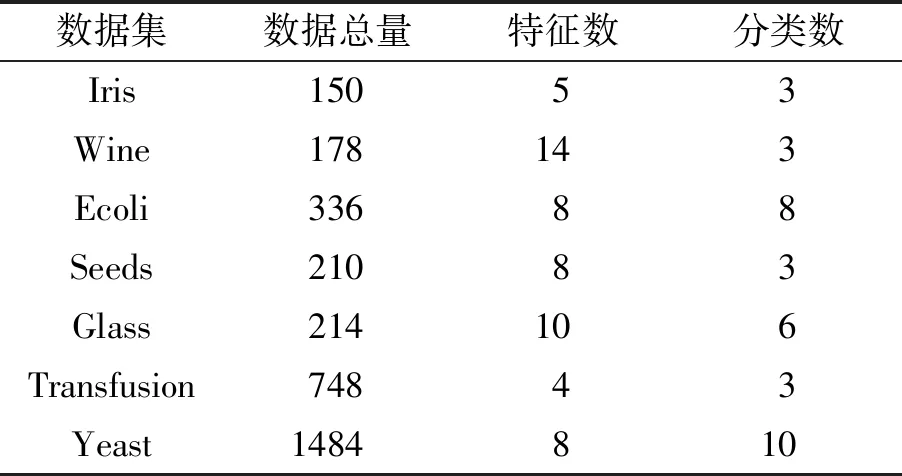
表3 分类数据集的详细信息Tab.3 Information of classification datasets

表4列出了本文方法与其他改进的扩展置信规则库(EBRB)方法的比较，指标是分类的精度.由于EBRB根据训练集生成规则数，所以EBRB的规则数等于训练集的样本数远大于DBRB的规则数.本文方法在5个数据集上都达到了第一名，在另外2个数据集上也达到第二名.这一结果验证了本文所提方法的有效性，同时也表明本文所提出的方法在分类数据集应用上也具有较好的性能.

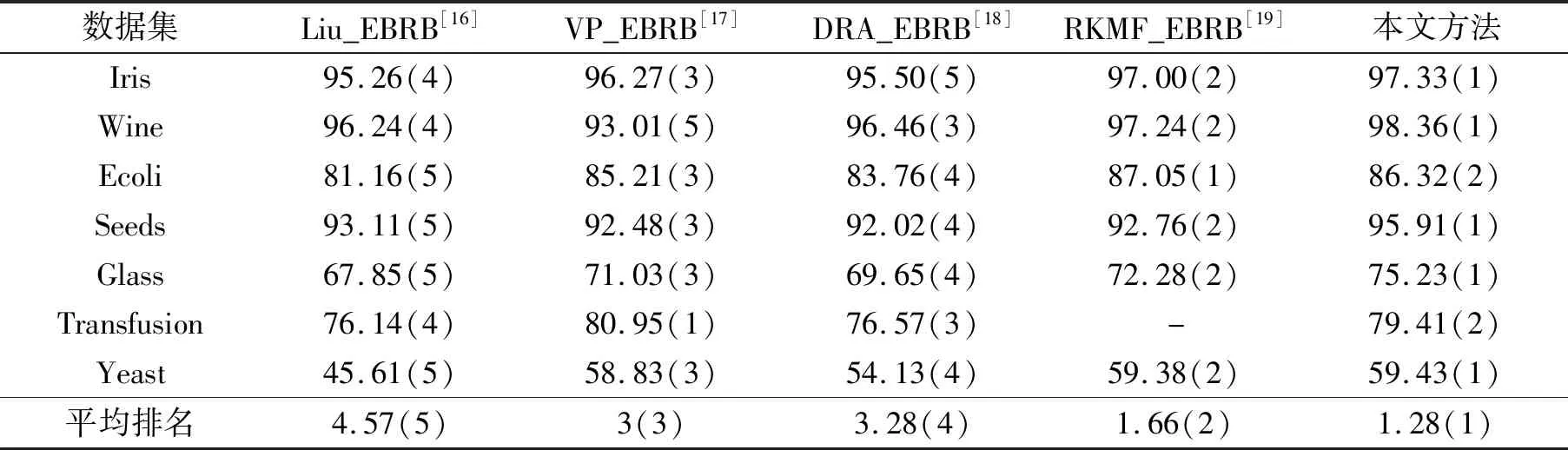
表4 与其他EBRB方法的比较Tab.4 Compare with other EBRB improvement methods

进一步将本文方法与其他传统的机器学习方法进行比较，对比实验结果为文献[20-21]中的部分结果.表5列出了比较结果，指标是分类的精度.结果表明，本文所提出的方法在大部分数据集上的精度都是排在第一名，表明本文所提出的方法具有良好的性能.

表5 与其他机器学习方法的比较Tab.5 Comparison with other traditional machine learning methods

4 结语

针对BRB-DL模型参数优化方法可移植性不足，应用效率低等问题，提出DBRB-DNN模型，并引入梯度下降算法对DBRB-DNN模型进行参数训练；同时对模型中受约束的参数进行预处理，避免在应用梯度下降算法时构建困难和效率不高的问题.最后，将BRB-DNN模型应用在分类问题上，扩展模型的应用领域.本文算法是基于Python平台实现的，可移植性更强.最后通过非线性函数的拟合实验、北京空气质量预测以及UCI上多个公共数据集的分类实验，验证所提出方法的有效性.不过本研究所选用的神经网络模型比较基础以及所有实验都是在规则完整的情况下进行的，没有考虑到规则不完整的情况应该怎么处理，今后将针对这一问题进行更加深入的研究.