集成2R1T并联机构的艾灸辅疗机器人概念设计与运动学分析
刁吉瑞,汤腾飞,方汉良,刘浩阳,张俊
(福州大学机械工程及自动化学院,福建 福州 350108)
0 引言
传统艾灸医疗难点在于治疗师需手动操作艾灸罐针对人体特殊部位进行灸法按摩,治疗过程中难以准确掌握温度大小、难以控制艾火以及燃烧烟雾对环境的污染,对医师的体力也有一定要求[1].目前,国内对艾灸辅疗机构的研究大多集中于艾灸盒、艾灸条等装置,鲜有关注辅疗机构的构型创新.
随着机器人技术的发展,一种串联形式的艾灸机器人出现在大众的视野中.戴耀南等[2]以人体背部能够恒定受温为目的设计了一种3轴艾灸机器人,可减少因人工操作失误而带来的医疗事故.夏世林等[3]提出一种可适用于多关节艾灸辅疗的机械臂艾灸器,其以6自由度串联机构为本体,末端装载艾灸器,通过结合温度控制系统解决了艾灸控温、定位、多角度治疗等难题.乐文辉等[4]基于机器人技术研发了一种4自由度串联机器人,基于D-H法验证了该机构的可行性,证明其可在简单位型下进行动作顺畅的医疗作业.然而,现有这类串联式艾灸机器人存在成本过高、运动形式单一的不足,难以满足艾灸辅疗流程对器械运动形式与工作空间的需求[5-6].在并联机构基础上通过集成串联机构搭建的混联机构,以高精度、小惯性、大承载能力及高刚度等潜在优势,被广泛用于航天、医疗、工业、农业等领域[7-11].其中,具有2R1T(两转动一平动)运动形式的少自由度并联机器人以灵巧性高、成本低、结构简单等优点成为诸多学者研究和探索的热点[12-16].以作者所见,尚未有将混联构型与艾灸辅疗结合的设计与应用实例.
为将混联机构应用于实际艾灸辅疗的基础作业,设计一种5自由度混联机器人机构,其并联模块构型为2UPS&1UPR&1UP,串联模块为2R(两转动)转头.以该混联机器人机构为研究对象,将从以下4个方面展开研究:
1) 运用螺旋理论分析2UPS&1UPR&1UP并联模块的自由度数目,确定机构具有2R1T的运动特性;
2) 推导运动学逆解表达式,建立全局雅克比矩阵并分析该机构奇异位型;
3) 通过“分层切片”的搜索原理预估机构工作空间;
4) 开展样机实验,检验上述理论分析的正确性.
1 概念设计与坐标系建立
如图1所示,艾灸辅疗机器人机构的并联模块分别由静平台、动平台、两条UPS支链、一条UPR支链和一条UP支链,串联模块是一个2自由度转头,用于放置艾灸盒.4条支链以炭纤维杆为主要承力构件,实现轻量化设计.其中,2条UPS支链呈对称分布,虎克铰(U)与静平台相连接,球副(S)与动平台相连接,移动副(P)的轴线分别通过虎克铰的中心点和球副的中心点,并且与U铰的两条转动轴组成的平面垂直.UPR支链中的U铰与静平台相连接,P副的轴线通过U铰中心点并与U铰的两条转轴组成的平面垂直.其中U铰的第一转轴与R副轴线平行.UP支链中的U铰与静平台相连接,P副的轴线经过U铰的中心点并且与两条转动轴线组成的平面垂直.第i(i=1,2,3)分支上与静平台相连接的U铰的中心点为Ai,第i分支上与动平台相连接的S副的中心点为Bi(i=2,3).B1是UPR支链中的转动副轴线的中心点.
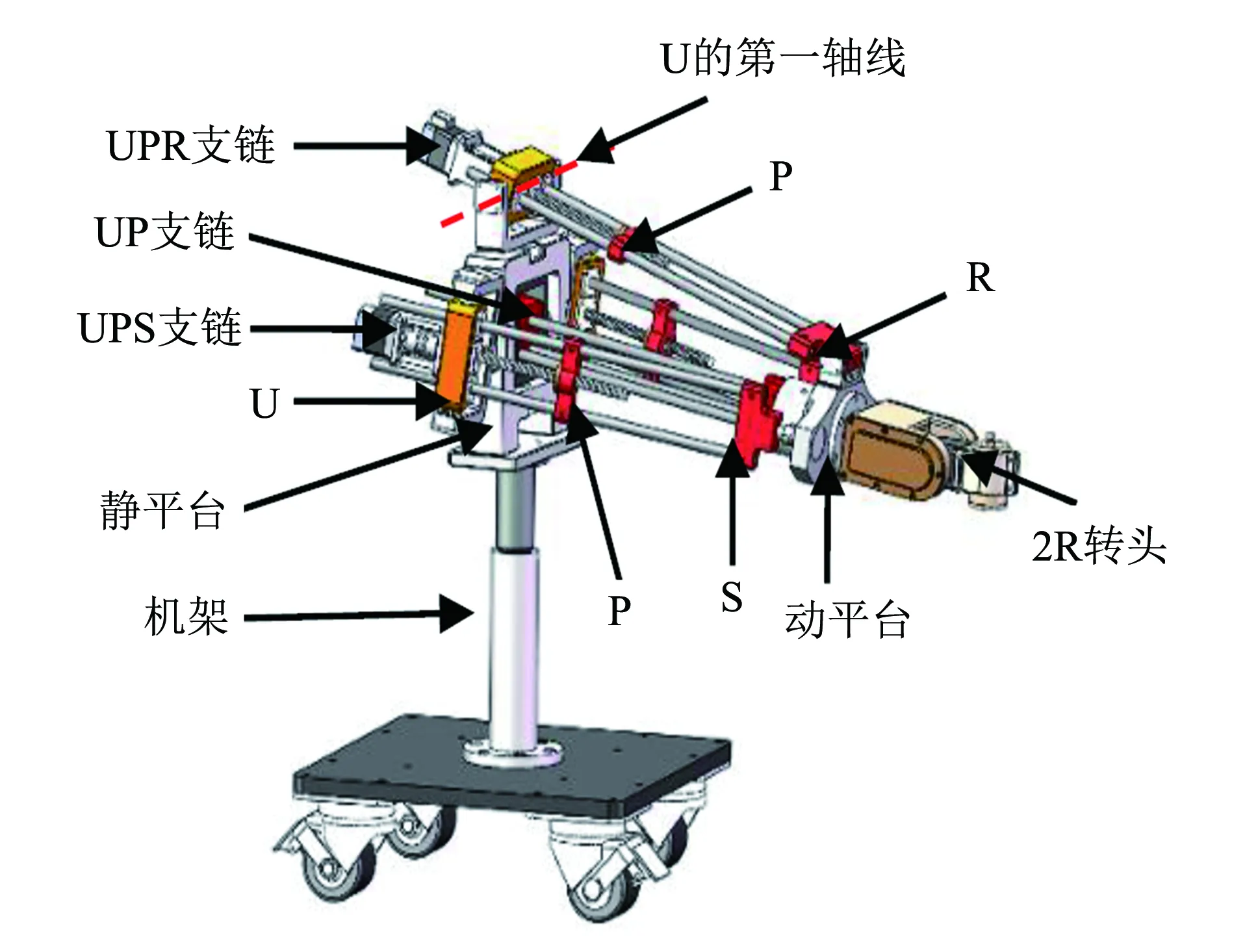
图1 2UPS&1UPR&1UP机构模型Fig.1 2UPS&1UPR&1UP mechanical model
综上所述,此概念设计可以实现整机及其各部件的模块化设计,以便根据不同艾灸辅疗方案需求快速重组机构,大大提高了该辅疗机器人在实际应用中的灵活性与可操作性.
建立如图2所示的静平台坐标系O-xyz、动平台坐标系O′-uvw、第一转头坐标系O′-x1y1z1和第二转头坐标系O″-x2y2z2.
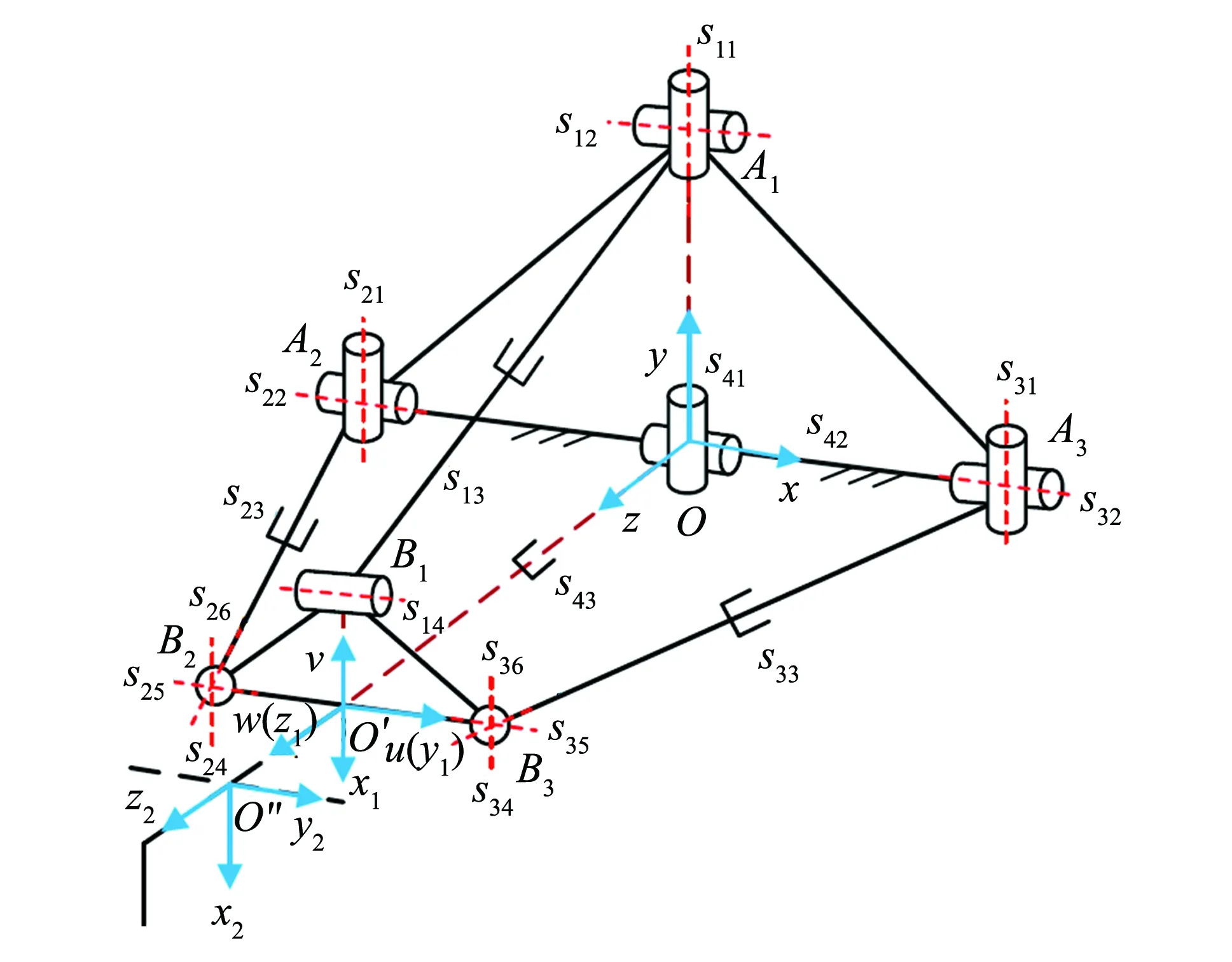
图2 2UPS&1UPR&1UP机构简图Fig.2 2UPS&1UPR&1UP schematic diagram of mechanism
图2中,原点O是A2A3的中心,x轴与A2A3共线,y轴与A2A3垂直,z轴方向向下.原点O′是B2B3的中点,u轴与B2B3共线,v轴与B2B3垂直,w轴方向向下.对于第一转头坐标系,z1轴与第一转头轴线重合,即与w轴重合,y1轴与第二转头轴线平行,x1轴满足右手定则.对于第二转头坐标系,O″为第一转头轴线与第二转头轴线的交点,y2轴与第二转头轴线重合,x2轴与艾灸条的方向平行,z2满足右手定则.ΔA1A2A3和ΔB1B2B3皆为等腰三角形.记sij为坐标系O-xyz下第i支链中第j个运动副的单位方向矢量.
2 运动学分析
2.1 自由度分析
根据图2所示并联机构的关节特征,并联模块的运动副向量的约束条件为:
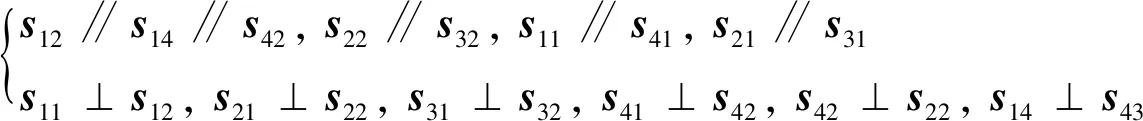
(1)
任意位姿下,UPR支链的运动螺旋系可表示为:
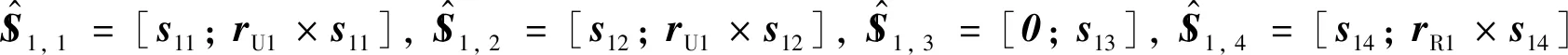
(2)
式中:rU1和rR1分别表示此支链中U副和R副的几何中心点在静坐标系下的位置矢量.
基于螺旋理论可求得该支链约束螺旋系为:
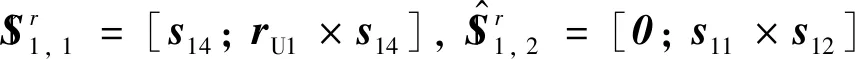
(3)
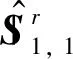
同理,支链2即UPS支链的运动螺旋系为:
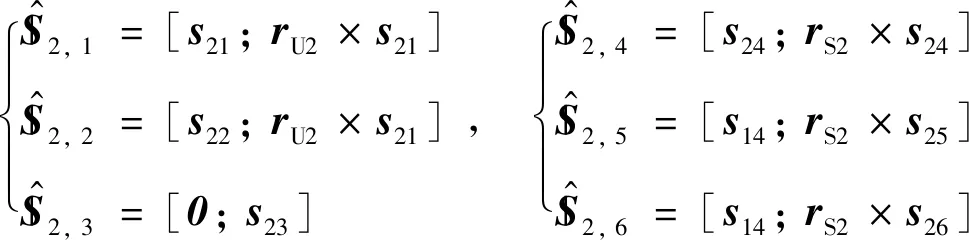
(4)
由互易螺旋理论可知,支链2、3不存在约束螺旋.对于恰约束从动支链即UP分支,在任意位姿下其运动螺旋系可表示为:
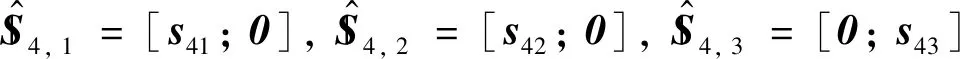
(5)
对式(5)求反螺旋可得:
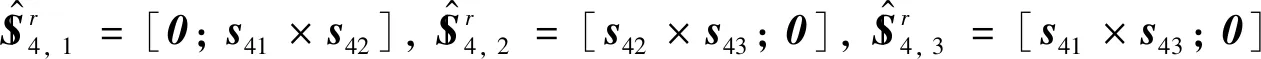
(6)
综合式(3)和式(6),可求得动平台的运动螺旋系为:
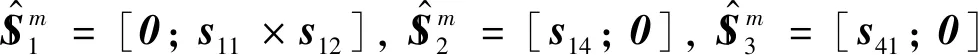
(7)
2.2 并联模块位置逆解
2UPS&1UPR&1UP并联机构的位置逆解分析是指已知动平台的姿态,求解3个分支移动副位移qi的过程.利用欧拉角φ、θ、ψ分别表示动平台绕z、y、x轴的3个姿态角,则动平台坐标系O′-uvw相对于静平台坐标系O-xyz的姿态转换矩阵可表示为:
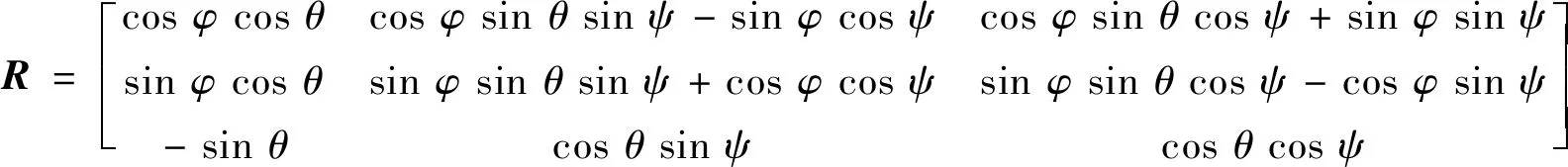
(8)
由并联模块各关节之间的约束关系可知:
si1·s14=0 (i=1,2,3),s14·rO′=0,s34·rO′=0
(9)

(10)
式中:rO′表示动平台坐标系原点O′在静平台坐标系下的位置矢量.
将rO′,si1和s14代入到式(9),可得并联模块的运动约束条件为:
φ=0,xO′=zO′tanθ,yO′=-zO′tanψsecθ
(11)
令ai表示在静平台坐标系O-xyz下Ai的位置矢量,bi表示在动平台坐标系O′-uvw下Bi的位置矢量,la和lb分别表示静平台和动平台各关节点到各对应坐标系原点的距离.上述矢量可表示为:
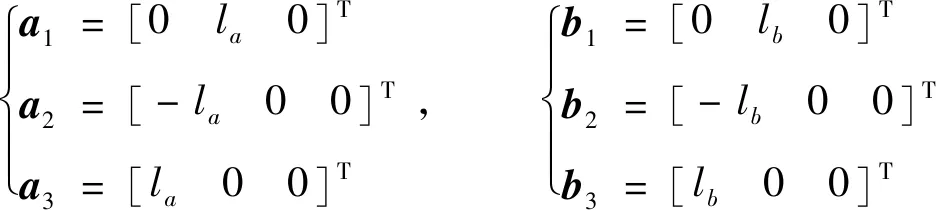
(12)
根据图2可知,机构的闭环矢量方程为:
qi+ai=rO′+R·bi(i=1,2,3)
(13)
则3个分支移动副的位移qi以及其单位方向矢量wi可表示为:
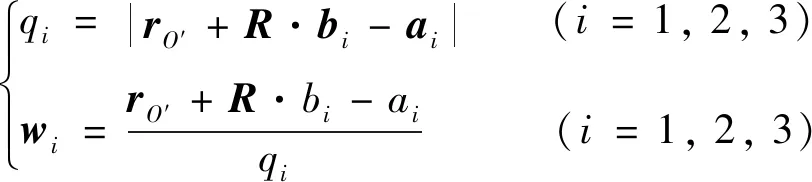
(14)
2.3 串联模块位置逆解
令第二转头坐标系O′′-x2y2z2相对于第一转头坐标系O′-x1y1z1的姿态转换矩阵为Ry2(θ2),第一转头坐标系O′-x1y1z1相对于动平台坐标系O′-uvw的姿态转换矩阵为Rz1(θ1),则第二转头坐标系O′′-x2y2z2相对于动平台的坐标系O′-uvw的姿态转换矩阵R1为:
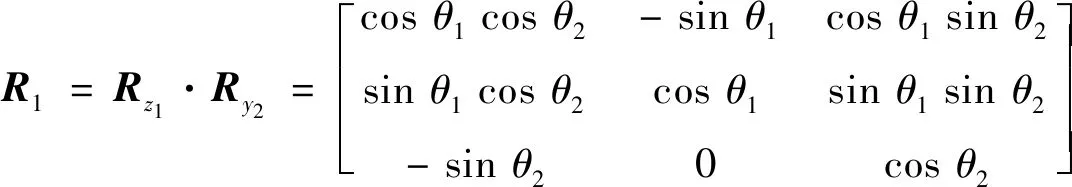
(15)
第二转头坐标系O″-x2y2z2相对于静平台的坐标系O-xyz的姿态转换矩阵R2为:
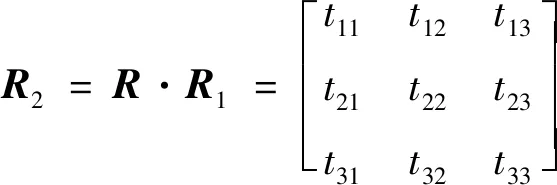
(16)
机构的末端点在静平台坐标系下的单位方向矢量可表示为:
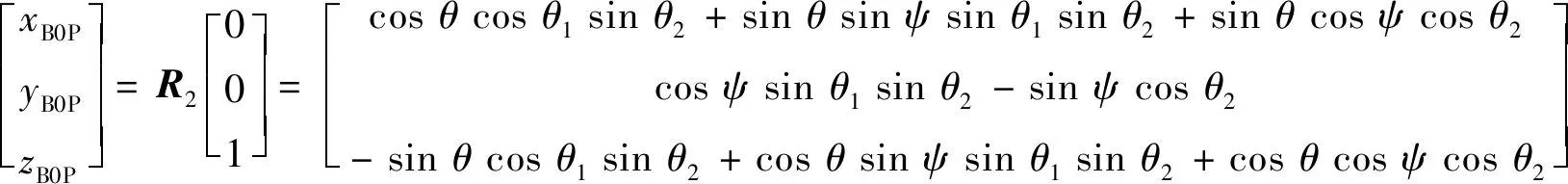
(17)
简化式(17),可得到以下3个方程:
sinψsinθ1sinθ2+cosψcosθ2=xB0Psinθ+zB0Pcosθ
(18)
cosψsinθ1sinθ2-sinψcosθ2=yB0P
(19)
cosθ1sinθ2=xB0Pcosθ-zB0Psinθ
(20)
机构末端点的位置坐标在动平台坐标系下可表示为:
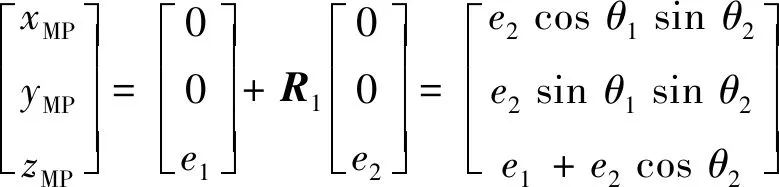
(21)
式中:e1表示第一转头坐标系原点与第二转头坐标系原点之间的距离;e2表示末端点与第二转头坐标系原点之间的距离.
此外,末端点的位置坐标在静平台坐标系下可表示为:
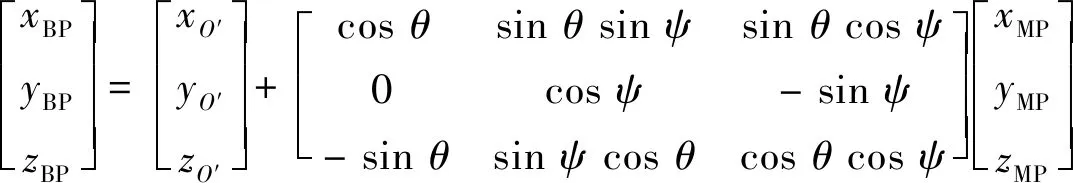
(22)
简化式(22)可得到:
xMPcosθ-zMPsinθ=e2cosθ1sinθ2
(23)
yMP=e2yB0P-e1sinψ-zO′tanψsecθ
(24)
zBP+e2sinθ(xB0Pcosθ-zB0Psinθ)-e2(xB0Psinθ+zB0Pcosθ) cosθ=zO′+e1cosθcosψ
(25)
联立式(18)~(25),在已知xB0P、yB0P、zB0P和xBP、yBP、zBP的情况下,分别给出zO′、θ、ψ、θ1、θ2的解析表达式,具体如下:
(26)
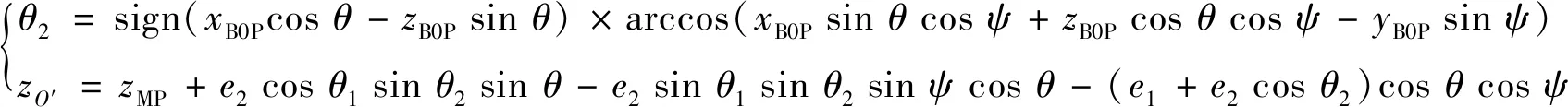
(27)
式中:
3 奇异性分析
在进行艾灸医疗作业的过程中不允许机器出现奇异位姿.因此,在将该并联机构用于实际艾灸辅疗之前需通过计算分析来预估机构的奇异位型.
为便于表述,不妨在动平台坐标系原点建立瞬时参考坐标系O′-x′y′z′,其3个坐标轴方向均与静坐标系3轴方向保持一致.同时,令vO′和wO′分别代表在瞬时参考坐标系下点O′的线速度和动平台的角速度,则动平台上Bi(i=1,2,3)的速度矢量可表示为:
vBi=vO′+wO′×(R·bi) (i=1,2,3)
(28)
此外,各支链移动副的线速度为:

(29)
将式(28)代入到式(29)中,并改写成矩阵形式为:
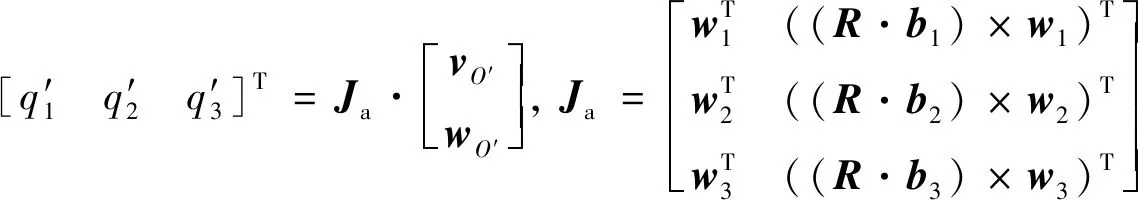
(30)
式中:Ja为3 × 6的驱动雅克比矩阵,表示动平台线速度和角速度与各支链移动副的线速度之间的映射关系.
在瞬时参考坐标系O′-x′y′z′下,动平台中心点O′瞬时速度可表示为:
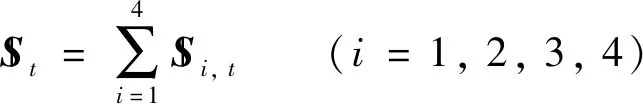
(31)
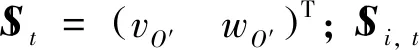
由式(3)和式(6)可知,4条支链在系O′-x′y′z′下的约束螺旋系为:
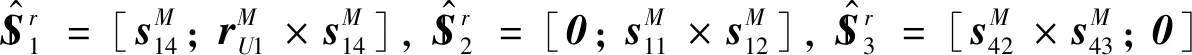
(32)
将式(32)代入到式(31)中作互易积,并将结果改写为矩阵形式:
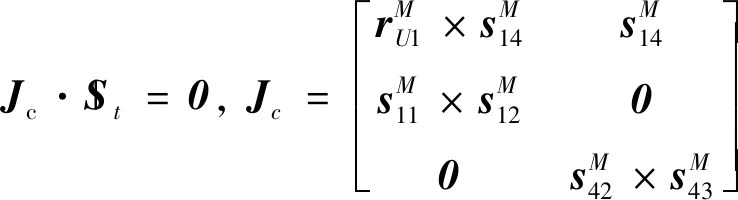
(33)
式中:Jc为3 × 6的约束雅克比矩阵,代表支链UPR和支链UP对动平台施加的约束力和约束力偶.
故全局雅克比矩阵可表示为:
J=[JaJc]T
(34)
该并联机构的奇异性分析可分为两种类型:约束奇异和结构奇异.因约束雅克比矩阵Jc中每一行皆线性无关,故其秩为3,则该并联机构不存在约束奇异.当驱动雅克比矩阵Ja的秩小于3亦或全局雅克比矩阵J的秩小于6时,机构存在结构奇异,即当机构处于如下状态时发生结构奇异:1) 3个支链的移动副共面,如图3(a)所示;2) 支链1或支链2平行于动平台,如图3(b)所示.

图3 并联机构的奇异位姿Fig.3 Singular position of parallel mechanism
通过合理设置机构尺度参数和s43⊥s22、s43⊥s32的约束条件,可以消除该并联机构的结构奇异位姿.
4 工作空间
少自由度混联机器人工作空间是指机构末端执行器的运动区域,是反映其定位能力的重要性能指标之一.根据上述虚拟样机的设计,并综合各支链丝杆的行程以及各关节转角的限制,可确定该艾灸辅疗机器人的基本尺度参数,如表1所示.表1中,qmin和qmax分别表示并联模块移动副长度qi的最小值和最大值;θS1、θS2、θS3分别表示S副关节3个转轴的转角,θU11、θU12(θU21、θU22)分别表示支链1(2)中U副关节的两个转轴的转角.θR表示的是R副关节轴线的转角.

表1 并联机构的尺度参数Tab.1 Dimensional parameters of parallel mechanism
采用“分层切片”的搜索思想来实现工作空间的求解,计算方法详见文献[17].经计算可得,该艾灸机器人的姿态工作空间如图4所示.进一步观察,由图4(c)和图4(d)可知,该并联机构在ψ=0° 和θ=0° 处可取得沿ψ、θ轴的最大工作截面,并且转角空间范围分别为[-43°,39°]和[-32°,32°],z向位置空间则在[160 mm,300 mm]区间内.此外,从姿态空间图中可明显看出,机构在z=190 mm处具有最大横截面,且随着z值不断增大,角ψ和θ的边界先增大而后逐渐缩小.从图4(b)或图4(c)中还可看出,该混联机床的可达工作空间以θ=0°截面呈对称分布,这与机构构型呈UPR支链对称分布的特点相吻合.并且注意到当z趋于最小值160 mm和最大值300 mm时,机构的角度运动空间范围极大缩小,故该艾灸机构在进行辅疗作业时应尽量避免将艾灸盒运动至工作空间的极点处.
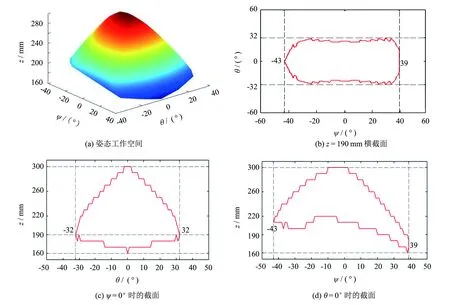
图4 并联机构的工作空间Fig.4 Workspace of parallel mechanism
5 实验结果与分析
为了验证上述理论分析的正确性,基于3D打印技术搭建了艾灸辅疗机器人的模型样机,如图5所示.该样机主要包括机器人本体、机架和控制系统.其中,机器人的各关节采用PLA(聚乳酸)通过3D打印机打印制造,支链体则采用碳纤维杆材料,机架作为载体,选择铝型材搭建;控制器采用研为八轴运动控制卡,并联模块采用42BYGH34型步进电机,串联模块采用28BYG30-7A型步进电机,驱动器与相应电机型号配套.
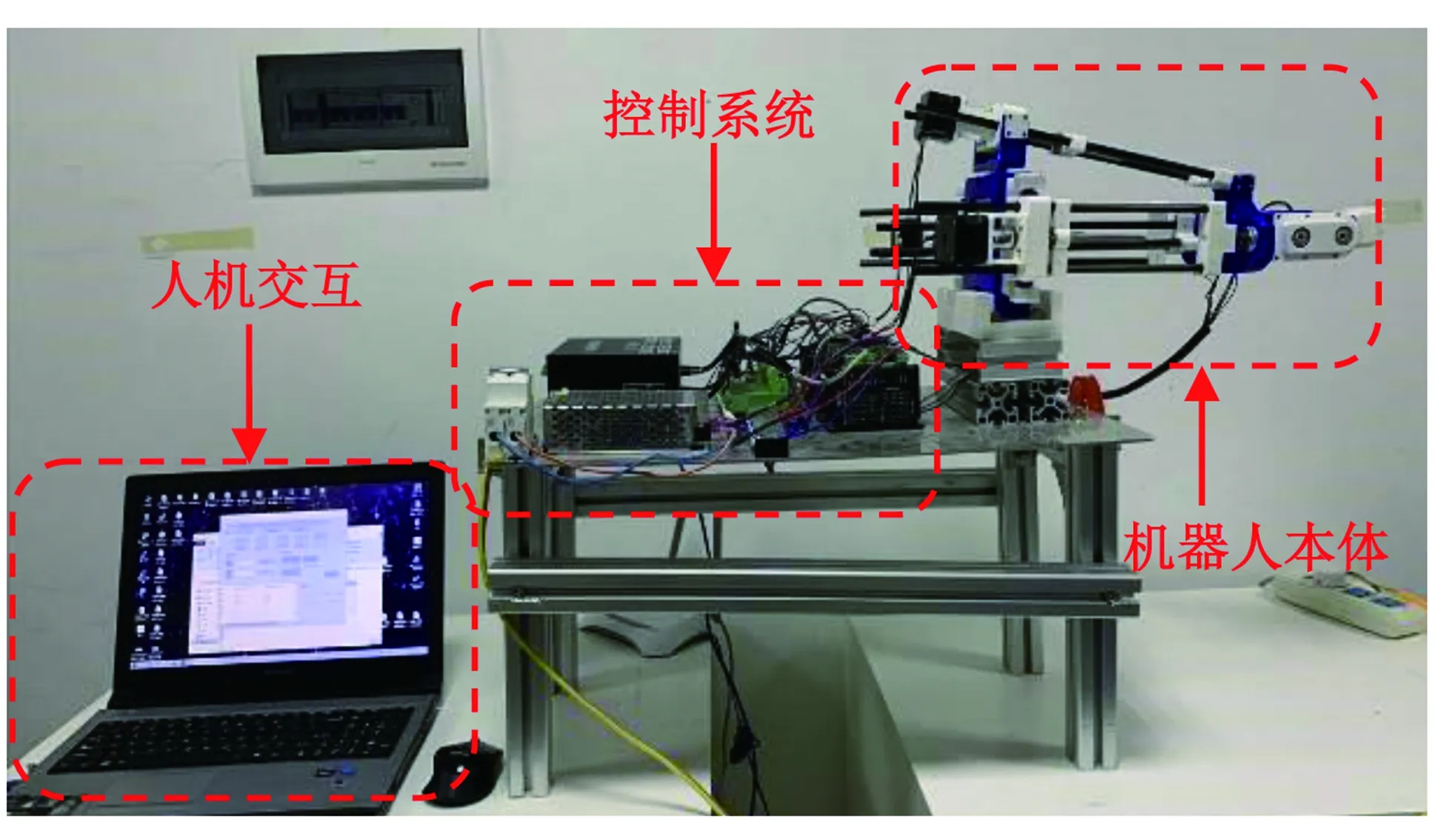
图5 艾灸辅疗机器人物理样机Fig.5 Physical prototype of moxibustion auxiliary therapy robot
为验证工作空间算法计算的准确性,将样机沿着z、x、y轴3个方向运动到如表2所示的关节极限位置,测量UP支链在动静平台间的长度以及与静平台之间的夹角,并整合测量数据.

表2 样机工作空间边界点Tab.2 Workspace boundary points of the prototype
为验证样机的运动自由度,以UP支链体平行于样机支架和二自由度转头处于相对水平为初始姿态,通过PC模块控制,使得样机动平台中心点分别沿着z、x、y轴3个既定方向运动,结果如图6所示.该结果与前述的自由度分析结果一致,验证了样机的3自由度形式.

图6 样机的不同位姿Fig.6 Different position of parallel mechanism
由上述实验结果可知,并联模块样机在可达工作空间内,x轴转角在[-41.6°,37°]之间,y轴转角在[-31.4°,31°]之间.这一转角范围,进一步验证了机构工作空间呈y轴对称分布的特点,也表明其可以满足艾灸辅疗对大摆角运动的需求.此外,样机末端中心点在保持ψ=0°和θ=0°的姿态下时,沿z轴方向的移动距离最低可至161.5 mm,与图4预估的工作空间分布基本一致,说明了在确定机构的尺寸参数后该工作空间算法的精确性.
注意到表2所示实测值与理论值之间存在偏差.造成这一偏差的原因是:样机在制造过程中采用的是3D打印技术,制造出的部件存在微小变形,并且在装配过程中关节间隙的大小存在不确定性,从而影响了机构的实际尺度参数.而在艾灸概念医疗中,这些微小误差造成的影响可忽略不计.
6 结语
1) 设计一种以2UPS&1UPR&1UP并联机构和2R转头组成的五自由度混联艾灸辅疗机器人.该混联机构能够实现空间z向移动及绕x、y转轴的转动,可实现多姿态的艾灸辅疗.
2) 基于螺旋理论分析并联模块2R1T的运动特性,以闭环矢量方程和串并联姿态转换矩阵求得艾灸辅疗机器人的运动学位置逆解.
3) 通过分析机构动平台的线速度与角速度求得全局雅克比矩阵,基于此矩阵明确了并联机构的奇异位姿.结果表明,该混联机器人不存在约束奇异,存在的两种结构奇异位型可通过拓扑构结构的约束避免.
4) 利用“分层切片”的搜索原理预估了艾灸辅疗机器人的位置工作空间.经分析可知该辅疗机器人具有较大转角,且工作空间呈θ=0°截面对称,与机构构型关于UPS支链对称的形式相吻合.
5) 基于3D打印技术搭建该混联机器人机构的物理样机,通过运动实验验证了上述运动学分析与工作空间预估的正确性.

