注意力机制的长短时记忆神经网络航线订座需求预测

陈思杰，傅仰耿

(福州大学计算机与大数据学院，福建 福州 350108)

0 引言

需求预测作为收益管理实施过程中的核心问题，多年以来一直受到国内外学者们高度的关注，预测的准确程度直接影响到了收益管理系统的可行性与价值，也直接影响着各个航空公司的票价结果与整体收益[1].在航空收益管理的需求预测方法之中，主要有三个方法：定量分析法、定性分析法、决策分析法.除了传统的需求预测方法外，近年来有不少学者也应用了许多新兴的智能预测算法和新兴技术，例如机器学习方法、大数据平台技术等.根据国内外研究现状可知，基于传统算法的需求预测模型依赖于精确的实验数据，并且算法工作量较大，模型的预测结果稳定性差，无法保证预测精度[2-4];基于智能算法的预测模型与之相比实用性较强，相较于传统算法精度和稳定性都有一定的提高.但是，航线订座需求预测受到各方面因素的互相影响，当下基于智能算法的航线订座需求预测研究较少，并且现有模型的预测精度仍然有待提高[5-7].为了提高航线订座需求的预测精度，提出基于注意力机制的长短时记忆神经网络(long short-term memory neural network，LSTM) 航线订座需求预测模型，首先对航线订座数据进行清洗与指标计算，然后利用注意力机制进行参数权重分配，最后通过长短时记忆神经网络算法对航线订座指标数据进行建模预测，对预测模型参数进行调整优化，得到航线预测模型后代入数据计算结果作为航线订座需求的最终预测值，以此构建航线订座需求的预测模型，实现对航线订座变化情况的预测.

1 数据准备

1.1 数据采集与预处理

本研究数据为国内某航空公司2017—2019年期间的航线飞行历史数据，包含该航空公司国内直飞航线在这三年当中共571 959条的订座离港数据.历史与预售数据的采集主要通过数据接口从中航信的离港控制系统(departure control system，DCS)与订座控制系统(inventory control system，ICS)中采集得到.DCS系统具备旅客值机、航班控制、登记控制等信息服务功能，ICS系统具备的功能是能够提供包含航班信息、座位控制、运价管理、销售控制等订座数据.针对采集数据的异常情况，总共做了以下几方面的处理：1) 对于航线日期数据存在异常的情况，统一进行了判断修正，并以‘YYYYMMDD’的格式进行存储；2) 对于存在旅客人数为0或者NULL的采集异常数据，将此类数据从数据集中进行剔除；3) 对于航班总布局数存在异常的情况，通过参考历史同航班数据的航班总布局数目进行修正补充；4) 对于存在的数据缺失，航班数目不全的情况，通过利用离港系统不同数据接口所得到的数据进行相互补充，尽可能地保证数据集合的完整性.

在航线需求预测实验中，对于源数据总共处理得到包括订座数、客座率、月份、星期、分配座位数、折扣率、节假日标识、预售数1、预售数2、预售数3共10个特征指标，每条航线共包括了2017，2018，2019年的实验数据，以厦门-上海航线在2017年1月份第一周的数据作为示例，数据预处理后得到的结果如表1所示.

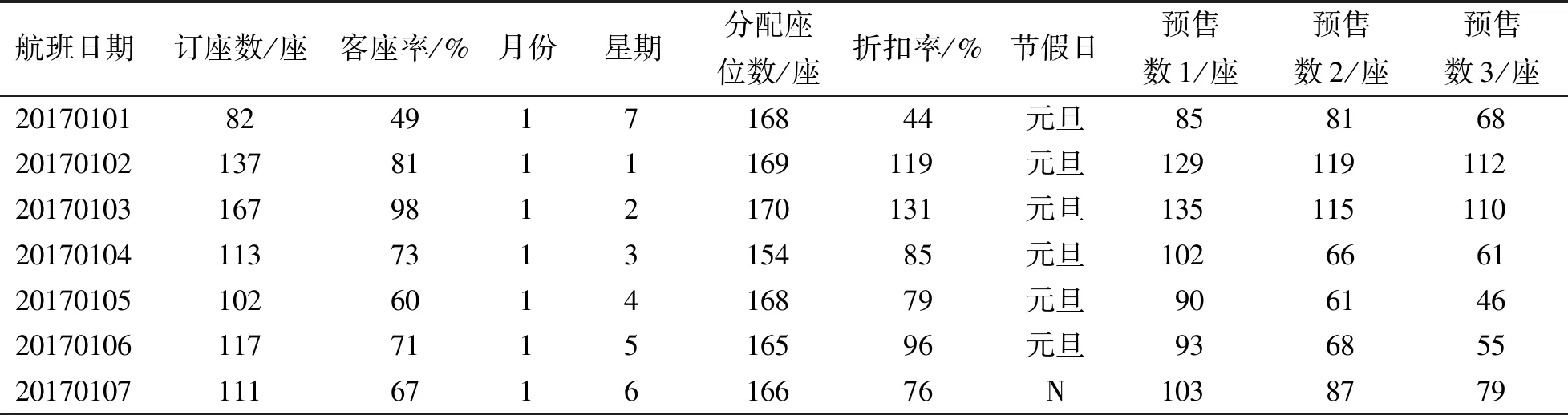
表1 实验中使用的厦门-上海航线数据集Tab.1 Xiamen-Shanghai route dataset used in the experiment

1.2数据标准化

为了使10个不同维度的特征数据在数据上具备一定的比较性，在构建预测模型之前，首先对10个不同维度的特征数据进行标准化与归一化操作，按一定比例将数据进行缩放，使数据值全部都落入一个小的特定区间.由于节假日标识特征属于类别数据，因此，在做归一化操作之前，需要对该类别数据进行数据化操作.数据化操作的方式是通过对类别数据进行标签编码将其转换成连续的数值型变量，把不是连续的文本或数字通过标签各做一个编号.经过标签编码处理后，节假日特征指标编码关系如下：N标签记为0，中秋编码为1，五一编码为2，元旦编码为3，国庆编码为4，春节编码为5，清明编码为6，端午编码为7，详见表2所示.

表2 实验中使用的节假日标签数据集Tab.2 Holiday label dataset used in the experiment

2 航线订座需求预测方法

航线订座需求预测问题与问题前序预测结果存在着较为紧密的关联，航线需求数在时序上呈现一定的周期性波动，随着时序的长期移动，预测值与前序预测结果整体上具备相同的变化趋势.此外，考虑到航司收益管理的定价政策，前序预测值与航线预售结果往往对航司票价折扣的波动有着关键的影响，因此，将LSTM神经网络算法应用在该具备时间序列特征的场景中是可行且具备一定优势的.

本研究算法的基本实现过程如图1所示，整体可以划分为：历史数据与预售数据的采集,对采集数据的清洗与过滤,根据采集数据计算特征指标数据,对数据进行标准化,由数据构建LSTM航线需求预测模型这几大步骤.

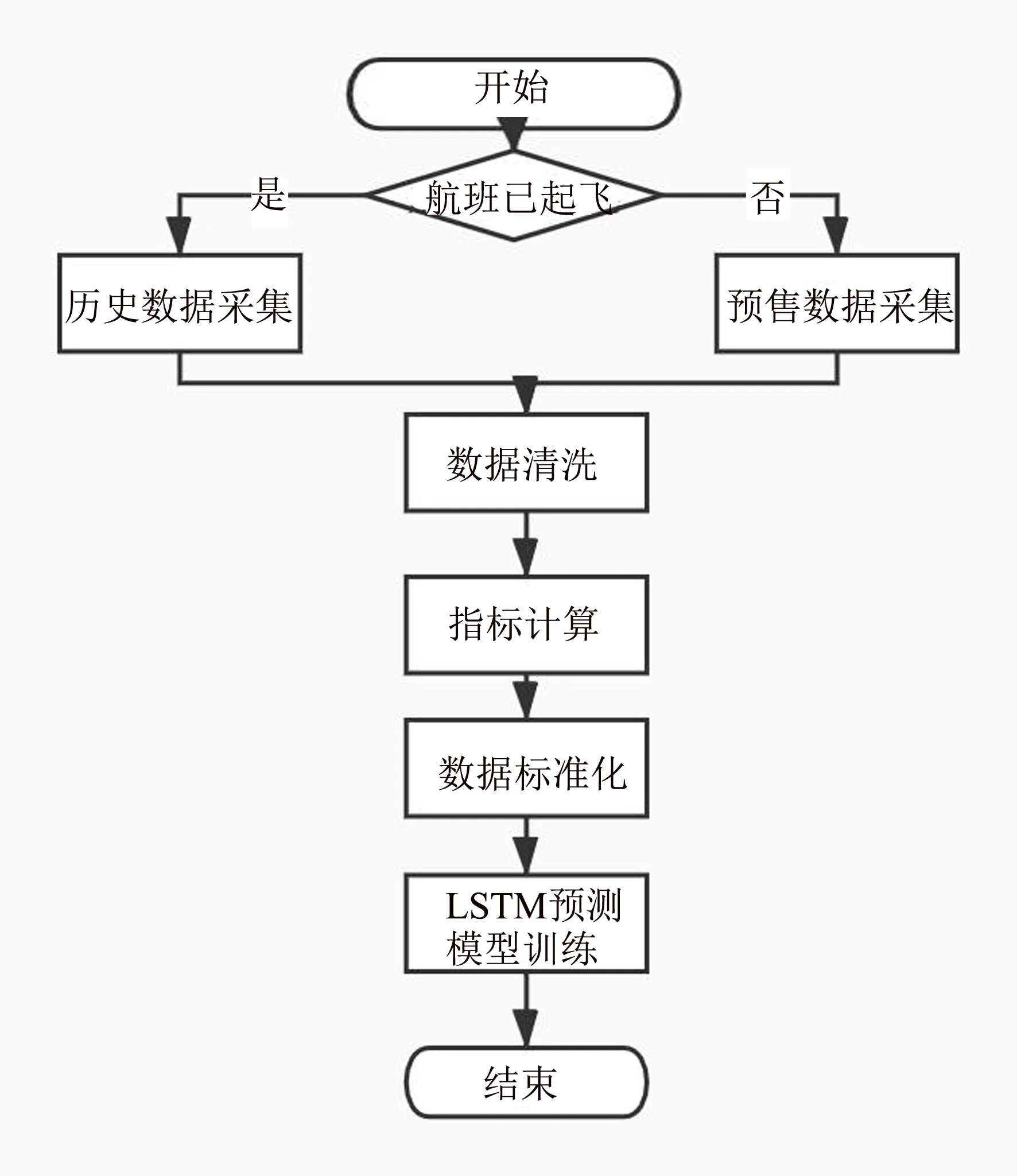
图1 算法实现过程图Fig.1 Algorithm implementation process diagram

2.1 注意力机制

注意力机制的原理可以概括为以下三个步骤，首先是通过query和key进行相似度的计算，从而获得权重值；然后需要对获得的权重值进行归一化处理，使其直接可用；最后将处理后的权重值与Value进行加权求和.

注意力(Attention)机制的本质思想如图2所示，由一系列的键值组合〈Key,Value〉数据对元素共同构成了Source.Target中的元素Query通过Source，计算与各个Key的相关性或者相似性，得到每个Key映射到相应Value的权重系数.再对Value做一个加权求和操作，便获得了Attention的最终结果数值.

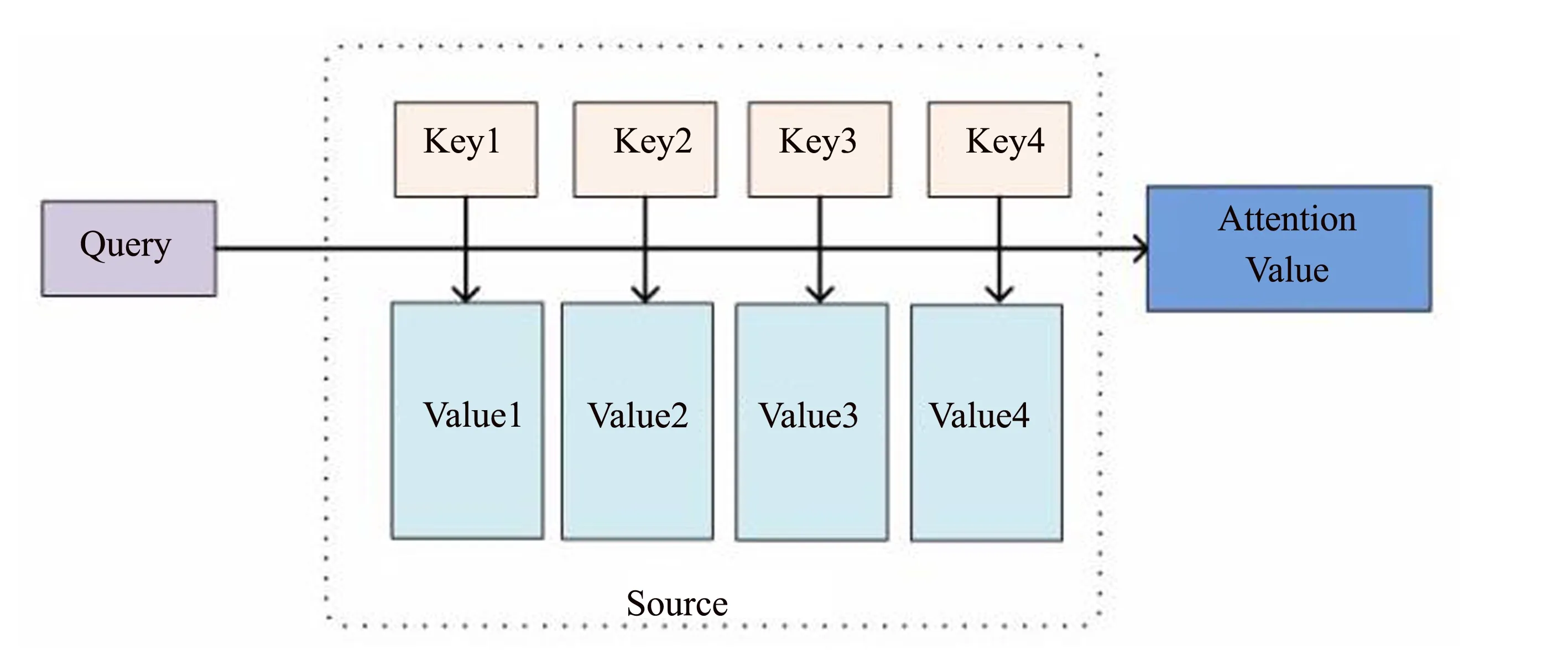
图2 Attention机制Fig.2 Attention mechanism

2.2 长短时记忆神经网络

长短时记忆神经网络是具备反馈结构的一种神经网络，其为循环神经网络(recurrent neural network，RNN)的变种，该神经网络巧妙地解决了RNN的长期依赖问题[8-9].由图3所示，LSTM的循环结构体中被设计成了由三个门结构组成，即输入门、遗忘门以及输出门[10].其中，输入门用于处理当前时刻下的输入，其输出是由两部门内容组成.一部分是ht-1和xt经过激活函数sigmoid得到的输出结果it,另外一个部分则是通过了激活函数tanh后得到的输出结果at,输出结果it和输出结果at两者进行相乘后再对细胞状态进行更新,其数学表达式为：

图3 LSTM示意图Fig.3 LSTM schematic

it=σ(Wiht-1+Uixt+bi)

(1)

at=tanh(Waht-1+Uaxt+ba)

(2)

其中：Wi,Ui,bi,Wa,Ua,ba代表线性关系的系数和偏倚，σ代表激活函数sigmoid.输出门负责计算并输出隐藏状态ht，隐藏状态ht由两个部分组成；第一个部分是由上一个时刻的隐藏状态ht-1与本时刻的输入xt通过激活函数sigmoid后得到的at；第二个部分则是由本时刻新的隐藏细胞状态Ct通过激活函数tanh后得到.其数学表达式为:

ot=σ(Woht-1+Uoxt+bo)

(3)

ht=ot⊙tanh(Ct)

(4)

遗忘门是用来控制是否遗忘，以一定概率控制是否遗忘上一层的细胞状态，其输入包括上一时刻的隐藏状态ht-1和本时刻的输入xt,两个输入通过激活函数(一般为sigmoid函数)后得到遗忘门的输出

ft.因为经过sigmoid激活函数后的输出范围在[0,1]，所以遗忘门的输出ft代表的含义是对于上一时刻隐藏状态的遗忘概率，其数学表达式为：

ft=σ(Wfht-1+Ufxt+bf)

(5)

其中：Wf,Uf,bf代表线性关系的系数和偏倚，σ代表激活函数sigmoid.LSTM除了和RNN一样会在每个序列索引位置向前传播隐藏状态ht之外，另外还多了一个隐藏状态Ct，这个隐藏状态通常称为细胞状态[11]，Ct在LSTM的结构如图4所示.Ct只与少量的线交互，像传送带一样，将数据直接运行在整个链上，并受到各个控制门的影响.

图4 LSTM示意图Fig.4 LSTM schematic

2.3 基于注意力机制的LSTM航线订座需求预测模型

本研究实验数据采集存储于oracle 11g数据库中，实验环境基于python 3.7.0，基于python的keras人工神经网络库处理数据并建立预测方程.采用LSTM神经网络算法对标准化和归一化后的实验数据进行训练和预测，训练过程首先以7∶3的比例将数据集合划分为训练数据和测试数据.以厦门-上海航线为例，包含2017—2019年期间经过加工处理后共1 095条航线数据，其中，训练数据767条数据，测试数据328条数据.完成数据集的划分后，需要将准备好的数据集转换构造为监督学习问题，考虑到上一个时间段对当天航线订座数的影响，将监督学习问题的框架作为航线条件和订座情况在前一个时间步骤预测航线订座数，构建数据集通过前n天的航线需求数据对当天的航线订座数进行预测，这里n表示时间步长参数，需要通过实验对参数进行调整确定.

由于当前数据集是按照航线起飞日期依次排序的时间序列数据集，实验过程首先对标准化后的数据集合做了一次转化预处理，使得数据集能够满足条件用于最近n天需求情况对当天航线订座数进行多步预测.通过把时间序列数据转换成一组包含成对输入输出的序列数据的方式，使得问题间接转化为监督学习问题，转化的核心方法是用到了Pandas所提供的shift()函数.对于一个给定的DataFrame数据，shift()函数实现了对输入的列进行复制，并将该列复制的副本数据往后或者往前移动，其中，移动后存在的数据空位会用NaN进行填充.通过上述操作，创建出了滞后值的数据列，通过观察值与滞后值的数据列，便能够较好地得到一个监督学习数据集的格式数据.以时间步长n=7时为例，处理后的数据格式如图5所示.

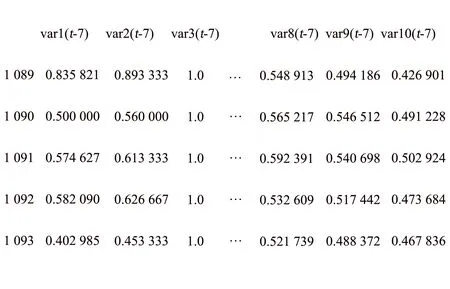
图5 监督学习数据集Fig.5 Supervised learning data set

采用多变量输入数据拟合LSTM模型，将输入(X)重构为LSTM预期的3D格式，即[样本数，时间步长，特征]，对于训练数据，重构后即为[767,n,10]的格式.针对航线订座需求预测场景，为了能够更好地捕获重要信息，在设计航线需求预测模型时引入注意力机制用于权重参数的分配，在输入层(LSTM)之前加入Attention.为了满足注意力结构里Dense层的输入格式，Attention的设计首先通过Pemute对输入的第1和第2个维度进行置换，置换后输出格式为[特征，时间步长]，然后将格式为[特征，时间步长]的数据输入到激活函数为softmax的Dense层，计算得到每个特征的权重.通过Dense后，需要用Permute再次对维度进行变换，完成变换后利用Multiply层完成Attention的第二个结构，用权重乘以输入，便完成了模型中注意力层的设计.对应参数分配结构图,如图6所示.

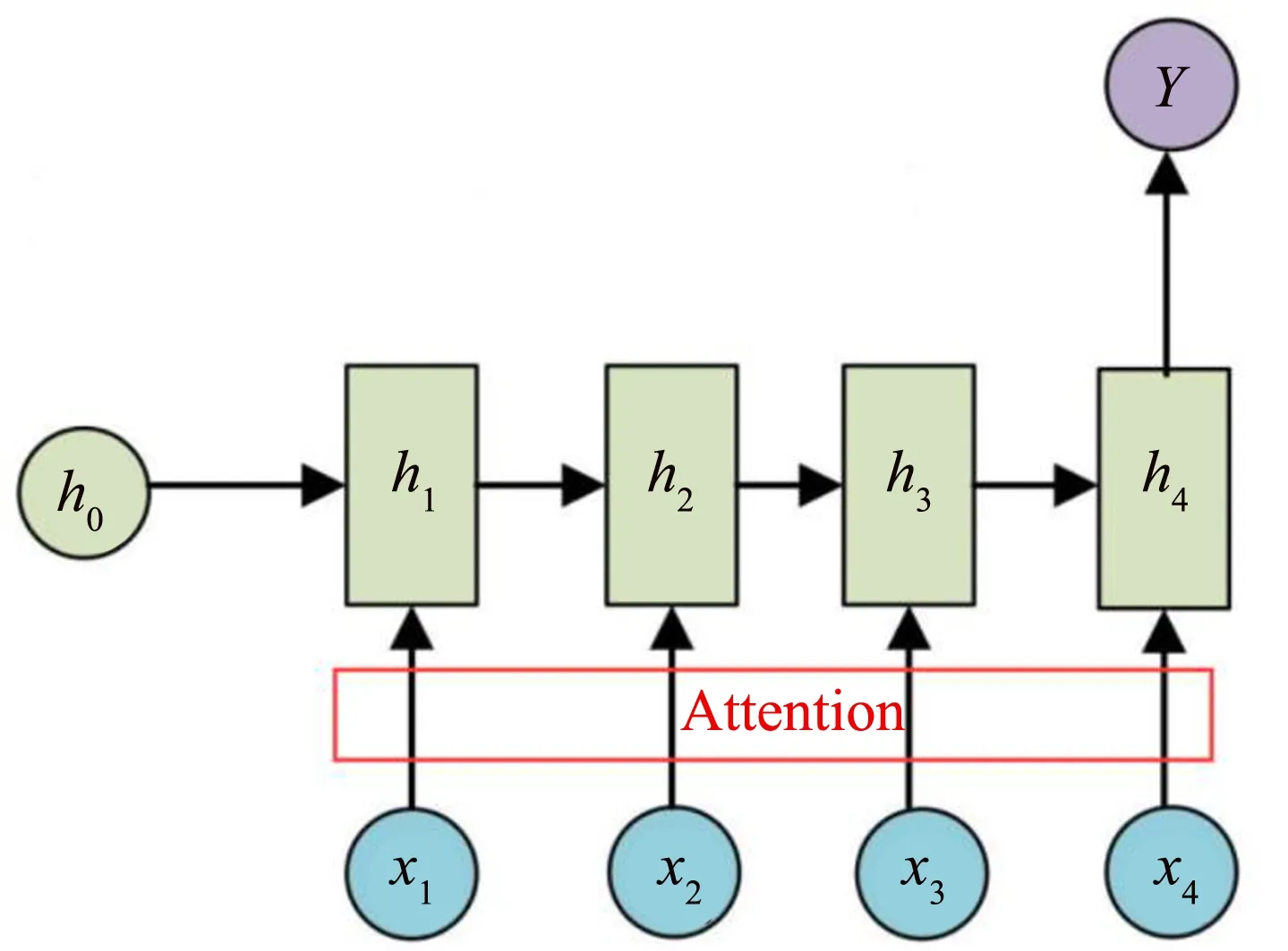
图6 参数分配结构图Fig.6 Parameter allocation structure diagram

通过注意力层的权重分配后，将得到的格式为[样本数，时间步长，特征]的数据输入到LSTM层，利用Adam 算法不断优化调整预测模型参数，对训练数据集合进行调参训练，主要针对units，epochs，batch_size进行调参.其中，units参数为整数，代表输出维度，指的是LSTM神经网络中包含的前馈神经网络中的隐藏神经元个数.epochs参数为整数，代表训练的总轮数，当没有设置initial_epoch时，模型的训练将会在轮次达到epochs参数所设置的值时停止.batch_size参数为整数，代表模型训练中进行梯度下降的每个batch使用的样本数，每一个batch的样本在模型训练的过程中会被计算一次梯度下降，对目标函数进行优化.以厦门-上海航线的LSTM预测模型为例，经过多次调参与测试，最终units参数设置为60，epochs参数设置为200，batch_size参数设置为60.确定了上述参数后，将时间步长参数n在[3,10]区间内分别取值进行调参实验，根据n的不同取值，预测实验结果如表3所示.

表3 时间步长调参结果Tab.3 Time step tuning results

根据调参结果，时间步长n在取值7时平均绝对误差指标(mean absolute error，MAE)与均方根误差指标(root mean square error，RMSE)结果最优，分别为13.1与17.2，绘制损失函数如图7所示.

图7 厦门-上海航线loss函数Fig.7 Xiamen-Shanghai route loss function

3 实验结果与分析

为了验证本研究提出的预测模型性能，分别采用收益管理领域里传统需求预测定量分析法的常用方法：移动平均法、指数平滑法,以及新兴的神经网络预测方法如RNN神经网络算法[12-13]、CNN-LSTM混合模型[14]对航线订座需求预测进行实验验证与对比分析.以厦门-上海航线为例，多次实验后取平均值，LSTM与各预测算法的实验对比结果分别如图8～11所示.其中，纵坐标表示航线订座人数，横坐标表示测试样例.

通过对比图8～11中预测值与真实值的曲线图，直观地看出，移动平均法与指数平滑法这两个传统的需求预测方法的预测结果都不理想，整体预测数值与实际值的偏差较大，曲线上下波动无规律，通过实验曲线可以明显地看出这两个传统算法在本次实验预测中出现了严重误差，全都较大偏离了真实值.RNN神经网络的预测曲线相比于传统预测方法来看整体结果较好，但是预测结果整体偏大，预测值的精度相较于Attention-LSTM神经网络较差，与真实值之间的偏差较大.CNN-LSTM混合模型应用于股票指数预测中具有较好的效果[14]，然而应用在航线需求预测中的实验效果并不理想，整体预测结果偏差较大，曲线趋势平缓，对于峰值的预测效果较差.相比之下，基于注意力机制的LSTM预测模型得出的预测结果准确性和稳定性都有显著提升，且对于曲线中的峰值情况的预测结果相比于传统预测方法，RNN神经网络及CNN-LSTM混合模型也较为接近，偏差值较小，预测效果更为准确.

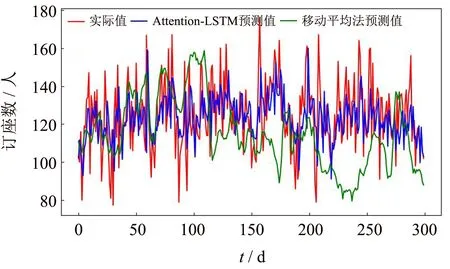
图8 Attention-LSTM与移动平均法预测对比Fig.8 Attention-LSTM and moving average prediction comparison

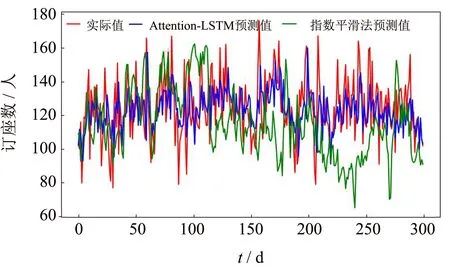
图9 Attention-LSTM与指数平滑法预测对比Fig.9 Attention-LSTM and Exponential smoothing prediction comparison

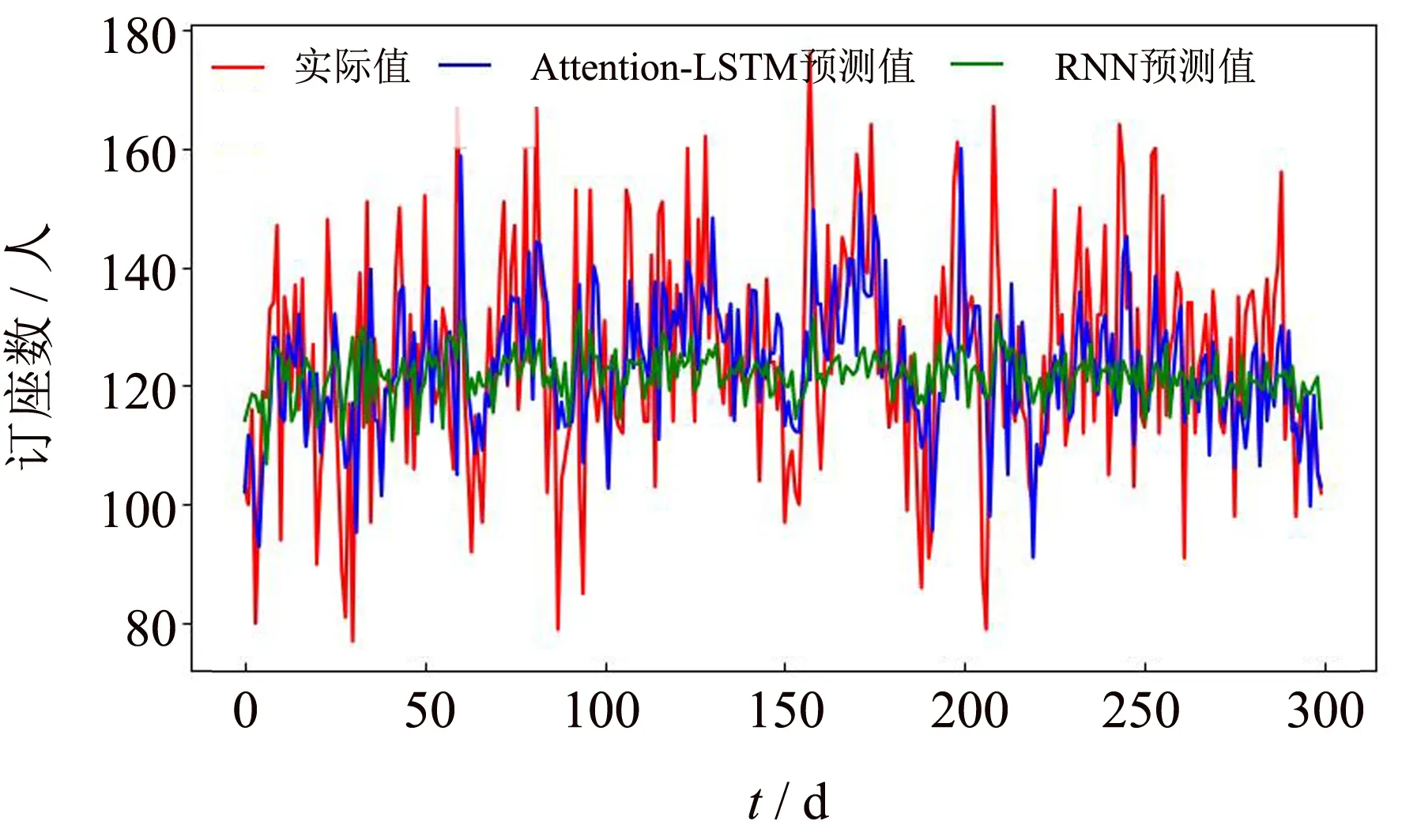
图10 Attention-LSTM与RNN预测对比Fig.10 Attention-LSTM and RNN comparison

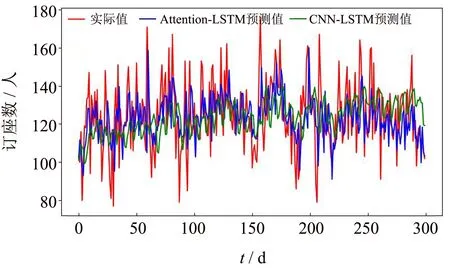
图11 Attention-LSTM与CNN-LSTM预测对比Fig.11 Attention-LSTM and CNN-LSTM comparison

根据预测结果与实际真实值计算出实验结果的平均绝对误差指标与均方根误差指标进行定量分析评价.平均绝对误差(MAE)是所有单个观测值与算术平均值偏差的绝对值平均，由于其能够解决误差相互抵消的问题，因而能够准确反映实际预测误差的大小[15];均方根误差(RMSE)是预测值与真实值偏差的平方与观测次数n比值的平方根，可以用来衡量观测值同真实值之间的偏差[16].MAE和PMSE的计算公式分别为：

(6)

分别采用移动平均法、指数平滑法、RNN神经网络算法、CNN-LSTM混合模型进行对比实验，对航线订座需求预测进行实验验证.表4为各预测模型的统计结果.

表4 预测误差统计结果Tab.4 Forecast error statistics

由表4可知，基于注意力机制的LSTM模型预测精度最高，其MAE结果为13.1，RMSE结果为17.2，与移动平均法相比，MAE降低了43.0%，RMSE降低了39.9%；与指数平滑法相比，MAE降低了41.5%，RMSE降低了37.9%；与RNN神经网络算法相比，MAE降低了9.0%，RMSE降低了5.0%；与CNN-LSTM相比，MAE降低了13.8%，RMSE降低了11.3%.

总体来看，基于注意力机制的LSTM航线订座需求预测模型相比较于其他传统预测算法精度更高，预测结果明显优于文献中已有的移动平均法、指数平滑法等传统需求预测算法，也优于新兴的RNN神经网络算法以及CNN-RNN混合模型，该模型应用于航线订座需求时序数据变换趋势的预测上明显提高了精度，可以更加准确地对航线需求的订座规律和变化趋势进行预测.

4 结论

提出的基于注意力机制的LSTM航线订座需求预测模型具有较好的预测效果，可以较好地拟合历史预售数据、航线布局、航线日期与航线订座需求之间的关系，提高了对未来航线订座情况的预测精度，为航线订座需求的预测提供一种新的思路和方法.将基于注意力机制的LSTM航线订座需求预测模型与传统的需求预测方法、RNN神经网络算法及CNN-RNN混合模型进行实验对比，代入实例验证文中基于注意力机制的LSTM预测模型应用于航线需求预测的有效性与优越性.