混合模式磁流变阻尼器的机械腿减振控制

杨坤全，黄惠

(1.漳州职业技术学院汽车工程系，福建 漳州 363000；2.福州大学机械工程及自动化学院，福建 福州 350108)

0 引言

机器人是多学科交叉和技术综合的结晶[1],目前在生产、运输、军事等领域都发挥着重大作用.其中足式机器人因具有更接近生物的行动方式、较强的环境适应能力、可代替人类开展复杂且危险的工作、节约人力成本[2]等特征，而拥有广阔的应用前景.但实际使用过程中，机械腿在高速、重载、跳跃、崎岖道路等情况下，会发生很大的振动，影响到工作的稳定性.如何消除或抑制振动以保证机器人的稳定性是足式机器人研究的关键问题之一[3].目前使用的减振控制方法主要有被动减振控制、主动减振控制和半主动减振控制.

被动减振控制的原理是在系统中加入阻尼元件来吸收振动能量并转化为其他形式，或者改变结构使得系统质量得到优化分布而实现减振效果[4].常采用的方法有：在机器人脚底安装橡胶、泡沫[5-6]一类的软质材料或弹簧缓冲装置[7-8]来减小地面冲击，又或者模仿人脚的生理结构，在脚的侧面和后部扩大稳定支撑区域[9].虽然被动减振系统性能稳定、易于维护、针对高频振动减振效果较好，但其结构一旦确定，只对固定频率的振动起作用[6]，难以适应某些足式机器人的复杂工作场所.主动减振控制需要外部能源输入提供控制力，控制过程依赖于结构反应和外界干扰信息，具有适应范围广、控制效果好等特点，但其控制系统结构复杂，造价昂贵.而半主动控制综合了前两者的优点[10]，其中，磁流变阻尼器具有响应速度快、阻尼可调范围大、能耗较低等优势，是当前振动控制领域的研究热点[11].戴金桥等[12]使用磁流变阻尼器实现对柔性机器人关节振动的半主动控制，蒋楠[13]设计了一种旋转型磁流变液阻尼并将其应用于机器人腿中，通过不同的电流控制策略调整机器人腿与地面的相互作用，实现运动过程中的半主动控制.然而这些磁流变阻尼器的出力效果仍无法满足机械腿在特殊工况下的减振需求.

因此，本研究提出一种剪切阀-挤压混合模式磁流变阻尼器对机械腿进行减振控制的方法.该新型阻尼器相较传统磁流变阻尼器而言具有更大的出力，在阻尼通道处具有更为均匀的磁场分布以及更高的磁感应强度.在刚性地面与柔性地面之间，依靠模式切换可快速提供连续可调的阻尼力，满足足式机器人对复杂工作场所的减振需求.对该阻尼器进行动力学台架试验获取其动力学数据，建立其 Bouc-Wen 模型，基于遗传算法对模型参数进行辨识，建立机械腿的Simulink仿真模型，并采用天棚控制的方法进行减振控制，为足式机器人的机械腿减振提供了一种方法.

1 新型混合式磁流变阻尼器介绍

将现有的一种新型剪切阀-挤压混合模式磁流变阻尼器应用于机械腿减振控制，其结构如图 1所示，主要结构的尺寸参数，如图2所示.

图1 新型混合模式磁流变阻尼器结构Fig.1 New hybrid mode magnetorheological damper

图2 新型混合模式磁流变阻尼器主要结构尺寸(单位：mm) Fig.2 Main structural dimensions of new hybrid mode magnetorheological damper(uint:mm)

该阻尼器具体性能可参考前期研究[14].该阻尼器的重点创新设计在于：活塞和缸筒处都安装了两组励磁线圈，实现磁流变阻尼器在两种工作模式的转换.当在一般较轻负载的情况下，只给活塞线圈通入电流，不给套筒线圈通入电流，该阀处于剪切阀式的工作模式.在特定的极端负载的情况下，给活塞处和套筒处的线圈同时通入电流，此时该阀处于剪切阀-挤压式的工作模式，活塞杆向外输出较大的阻尼力.此款新型混合式磁流变阻尼器，可根据不同的场景，通过控制输入电流的大小，控制阻尼器的最大输出力，符合足式机器人对复杂工作情况的需求.

2 混合式磁流变阻尼器正模型

2.1 混合式磁流变阻尼器力学实验

为获取该混合模式磁流变阻尼器的力学数据，利用万能材料试验机进行测试，对活塞线圈和缸筒线圈分别提供不同的电流激励，测试阻尼器在不同工作模式下的力学性能，万能材料试验机测试现场如图3所示.

图3 阻尼器力学性能测试Fig.3 Mechanical performance test of damper

设置激励信号为正弦输入信号，当测试线圈分别通入 0.1，0.3，0.6，1.0 A电流时，剪切阀式下力与位移的关系如图4所示.实验结果表明，混合式阻尼器在剪切阀式下，对活塞两线圈施加1.0 A电流时阻尼器的最大出力可达1.065 kN；当测试线圈分别通入 0.1，0.3，0.6，1.0 A电流时，剪切阀-挤压模式下阻尼器力与位移的关系如图5所示.从图5中可见，剪切阀-挤压式阻尼力位移滞回曲线与剪切阀式阻尼力位移滞回曲线有所不同，剪切阀-挤压式在两端有尖角现象.主要原因是在剪切阀-挤压式下，磁流变液与活塞相互作用时会出现拉伸和压缩状态，从而导致尖角现象的发生.试验测试结果表明，当只给两线圈施加1.0 A电流时，混合式阻尼器在剪切阀-挤压式下最大出力可达4.939 kN.相比单一形式的磁流变阻尼器，混合式阻尼器可以使阻尼力的最大出力增加364%.

图4 剪切阀式下阻尼器力与位移曲线Fig.4 Force and displacement curves of damper under shear valve type

图5 剪切阀-挤压模式下阻尼器力与位移曲线Fig.5 Damper force and displacement curves in shear valve-squeeze mode

2.2 混合式磁流变阻尼器模型识别

由于磁流变液体的非线性，选用Bouc-Wen模型作为磁流变力学模型，它是目前应用最为广泛的非线性滞回模型，通过改变模型参数就可以模拟众多的滞回特性.该模型由滞回系统、弹簧和阻尼器并联而成，如图6所示.其模型方程可表示为：

图6 阻尼器力学性能测试Fig.6 Schematic diagram of Bouc-Wen model

(1)

由于Bouc-Wen力学模型具有多个未知参数、运算较为复杂，本研究采用遗传算法进行模型参数的识别工作.具体分为如下6个步骤：

1) 通过分析具体问题采用不同的编码方式获得初始种群；

2) 利用适应度函数计算出个体的适应度值；

3) 通过对个体适应度值进行评估将满足条件的个体遗传到下一代；

4) 在计算过程中设置一定比例作为种群的交叉概率遗传到下一代；

5) 设定种群中一定的变异概率，将新得到的种群再次进行适应度计算；

6) 对种群适应度值进行评估满足条件计算结束，否则继续对种群执行选择交叉变异直至收敛为止.

首先将混合式磁流变阻尼器试验数据进行稀释得到遗传算法的初始种群，确定初始种群的个数为N=40.基于上述实验位移幅值，对频率f=5 Hz时0～1 A的试验数据进行参数辨识，将辨识后得到的参数值代入所选的力学模型进行仿真.通过对比试验数据与仿真结果的吻合情况，来确定参数辨识结果的正确性.采用仿真值与实验值之差的最小平方值为适应度值，得出适应度函数具体的数学表达式为：

(2)

式中:fitness为适应度值；Fi，仿真值为第i个点的仿真值；Fi，实验值为第i个点的实验值;Fmax为初始种群中试验数据的最大值；Fmin为初始种群中试验数据的最小值；m为初始种群的个数.

滞回力模型：

滞回位移模型:

式中：由于试验中有具体的激励信号，因此活塞的相对位移x、相对速度v都能确定;n表示滞回曲线的圆滑程度，根据前人的研究经验设n=2;模型中的未知参数有c、k、α、γ、β、A共6个.

在确定好适应度函数之后，设置交叉、变异比例分别是75%和25%.在初次参数辨识求出一组未知参数值后，找出每个参数的变化范围，并将每个参数的最大值与最小值用来设置下次参数辨识的上下限，多次重复以上步骤直到每个参数达到预期精度.

2.3 辨识结果分析与验证

1) 剪切阀式下的辨识结果.在对初始种群辨识后得到参数的最小值作其参数LB，最大值作为其参数UB，不断重复上述操作.从而缩小模型未知参数的取值范围，因此最终参数识别的精度也不断提高.经过多组运算后得到的各参数值如表1所示.

表1 剪切阀式下各参数辨识结果Tab.1 Parameter identification results of shear valve type

2) 剪切阀-挤压模式下的辨识结果.混合模式下剪切阀-挤压模式辨识结果如表2所示.给活塞和缸筒内4个线圈同时通电，当活塞运动到缸筒中间时，形成剪切阀式；当活塞运动靠近左右端盖时，将会形成剪切阀-挤压式，此时阻尼力将会瞬间增大.因此在这种混合模式下，需要做两次参数辨识工作，但活塞运动到缸筒中间可近似看成只给两线圈通电时的普通剪切阀式，因此在混合模式下只需要对剪切阀-挤压式进行参数辨识，辨识过程和方法与普通剪切阀式类似.

表2 剪切阀-挤压式下各参数辨识结果Tab.2 Parameter identification results of shear valve-extrusion type

通过遗传算法参数辨识得出的模型可以适用固定电流下，但不能适用于一般情况，因此参数辨识的结果只能接近真实值无法等于真实值.为了找出精确的模型通用表达式，可根据刘永强等[15]将c、k、α看成与电流的函数关系，β、γ、A看成为某常数对该力学模型进行改进，将Bouc-Wen模型中的c、k、α表达成电流的二次函数关系，即：

(3)

结合Bouc-Wen力学模型将其表达为：

(4)

将阻尼器在不同电流下的试验数据作为遗传算法的初始种群，以式(4)力学模型利用遗传算法对其进行参数辨识，得出a0、a1、a2、b0、b1、b2、c0、c1、c2、γ、β、A的值.混合式MRF阻尼器通过参数辨识.

在剪切阀式下辨识结果为：

(5)

在挤压模式下辨识结果为：

(6)

为检验采用遗传算法参数辨识得出的未知参数值是否正确，将在不同电流作用下得到的参数值带入力学模型中进行仿真,如图7，图8所示，并与试验数据进行对比.从图7、图8中可知，在阻尼力-位移曲线中实验值(点线)和模型预测值(实线)没有完全吻合.因为Bouc-Wen并不是磁流变液真实力学模型，但基本能够表达磁流变液的力学特性，在图中具有较高的吻合度，因此得出采用遗传算法参数辨识求解出的参数值是相对准确的.

图7 剪切阀式下阻尼器力与位移曲线Fig.7 Force and displacement curves of damper under shear valve type

图8 剪切阀-挤压模式下阻尼器力与位移曲线Fig.8 Damper force and displacement curves in shear valve-squeeze mode

3 基于混合式磁流变阻尼器的机械腿模型

3.1 Simulink建模仿真

为简化机器人运动学求解过程，给机器人加入约束条件，一般是机器人在行走过程中身躯始终保持正直状态，而且机械腿与地面接触时处于完全接触状态，减振理论模型如图9所示.其中，机身质量为m，其振动位移为u(t) ；地面振动位移为v(t).

图9 机械腿简化模型Fig.9 Simplified model of mechanical leg

假设地面振动位移为：

v(t)=Asin(ωt)

(7)

式中:A为振动幅值；ω为角频率.

建立机械腿减振系统微分方程：

(8)

式中:c为阻尼系数；k为刚度系数；u(t)为机身位移；v(t)为地面振动位移.

机身位移为：

(9)

采用Simulink建立机械腿减振系统的仿真模型，在减振模型仿真过程中，减振数学模型为式(9)，具体的仿真流程如图10所示.

图10 机械腿仿真流程图Fig.10 Flow chart of mechanical leg simulation

在机械腿减振系统仿真过程中，只分析给4个线圈同时通电时，混合式MRF阻尼器的减振性能将地面激励信号设置为0～20 Hz的正弦扫频信号.MRF阻尼器的力学模型使用自定义模块完成，在扫频信号下，对减振系统在固定电流作用下的振动与地面基础振动进行仿真，得出减振系统在地面与机身的位移幅值仿真曲线如图11所示.将Simulink仿真结果进行处理并与理论对比，得出在不同频率下传递率的变化曲线如图12所示，图中结果表明理论推导与软件仿真的结果较为吻合，说明所建立的Simulink模型具有可靠性.

图11 机械腿仿真结果图Fig.11 Simulation results of the mechanical leg

3.2 天棚阻尼控制

天棚阻尼控制的基本原理是在簧载质量与天空惯性系之间模拟连接一个阻尼减振器，能够有效地抑制目标的振动.天棚控制模型是一种具有理想化的模型，本研究建立的天棚控制机械腿模型如图13所示.

图13 机械腿天棚控制模型Fig.13 Skyhook control model of mechanical leg

理想天棚模型时阻尼力为：

(10)

式中:csky为天棚阻尼系数.它由系统特性决定，其作用主要是调节机械腿工作来改善控制系统的平顺性，其原理是将产生的天棚阻尼力与其机身运动方向相反.即：

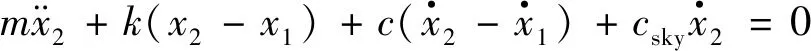
(11)

式中:m为机身质量;x2为机身位移;k为刚度系数;c为阻尼器的粘性系数.将上式进行拉氏变换得：

ms2X2(s)+k(X2(s)-X1(s))+cs(X2(s)-X1(s))+cskysX2(s)=0

(12)

解上式方程,可得到机械腿振动的传递函数为：

(13)

其加速度的频率响应函数为：

(14)

其中，由(13)、(14)式，并利用Matlab计算出机械腿天棚控制模型的幅频响应曲线，结合仿真曲线综合考虑取csky= 2 500 N·s·m-1.

在天棚控制系统中，磁流变阻尼器的输出力满足：

(15)

(16)

式中：Fmax为最大库伦阻尼力.

3.3 结果分析

在机器人减振领域，一般利用简谐信号与随机信号来测试减振系统的好坏，随机信号一般为白噪声信号，采用Simulink建立天棚控制的机械腿减振系统程序，如图14所示.

图15和图16是在振幅10 mm、频率为5 Hz的正弦信号下，混合式磁流变阻尼器机械腿的减振控制仿真结果，图17为随机信号激励下机械腿的减振仿真结果.从图15和图16可以看出，在正弦信号激励下，天棚控制相比通入固定电流，其振动幅值从6.8 mm下降到3.3 mm，降低了49%；加速度从7.5 m·s-2下降到4.0 m·s-2，降低了47%，都有较大程度的降低.图17结果表明,在随机信号激励下，机械腿振动位移也有大幅度降低，验证了该控制算法的控制效果和实用性.

4 结语

提出一种剪切阀-挤压混合式磁流变阻尼器对机械腿进行减振，对其力学性能进行试验研究.基于试验数据，选择合适的磁流变液力学模型，利用遗传算法对所选的力学模型进行参数辨识，并建立机械腿动力学模型.最后，在天棚控制策略下对机械腿进行了减振研究，得出如下主要结论：

1) 在混合式阻尼器实验中，得出在剪切阀式下阻尼力最大可达1.065 kN，在剪切阀-挤压混合模式下最大可达4.939 kN；

2) 采用遗传算法对磁流变液的Bouc-Wen模型进行参数辨识，得到新型混合模式磁流变阻尼器的力学正模型，且模型准确；

3) 将新型混合模式磁流变阻尼器应用于机械腿减振，配合天棚控制策略，能有效抑制机械腿振动，振动位移幅值与加速度分别下降了49%和47%.