基于泰勒级数的空间机器人时延神经网络控制

张宇涵，于潇雁，2，陈力

(1.福州大学机械工程及自动化学院，福建 福州 350108；2.流体动力与电液智能控制福建省高校重点实验室(福州大学)，福建 福州 350108)

0 引言

空间技术的发展为人类开拓宇宙提供了极大的便利，而太空环境多变，工作风险极高，因此空间机器人代替宇航员进行太空作业是目前的主要手段.目前为止，对高度自主的空间智能机器人的研究还在初步阶段，因而遥操作技术依然是人类探索太空的重要手段和主流研究.对于空间机器人遥操作控制系统来说，天地间距离过大，信号在传输过程中会产生时间延迟(简称时延).如果控制系统对时延影响不予考虑，其控制精度将会大大受到影响甚至导致系统控制失效.目前针对时延环境下空间机器人展开的研究相对较少.张建宇，叶柄能等提出了基于时延估计法的控制力矩设计问题[1-3],但它们均是为解决机器人参数不确定问题而设计的控制手段，而并非解决时延问题，其实际动力学系统中并不存在时延；白硕等展开了网络环境下工业机器人的时延预测研究，但地面网络环境并不适用于太空遥操作环境[4-7]；Chen等提出使用泰勒级数预测法来得到系统时延项，但他们未在三角函数展开式部分进行化简，导致系统模型过于繁冗，也未在空间机械臂系统上展开相关工作[8-10]；此外，上述研究均未对时延范围进行有效探讨.因此对具有时延的空间机器人系统进行研究，并给予良好的补偿控制手段[11-16]是非常有必要的.

针对上述问题与不足之处，本研究利用基于泰勒级数展开的预测手段，对关节空间坐标进行时延项的提取，从而得到改进的空间机器人动力学方程.与传统动力学方程相比，改进的动力学方程模拟了时延误差，更加符合客观实际情况；利用神经网络控制[14]对非线性函数项的逼近能力，弥补计算力矩法无法解决的时延误差；在神经网络控制器的基础上引入模糊和递归控制可有效降低系统的抖振并提升在线学习速度；同时对时延值的有效范围进行在线评估，在能提供良好品控的基础之上确定时延范围.利用本文所提出的控制器方案，可以实现对关节空间预设轨迹的精确跟踪.数值仿真验证了所提出方法的有效性.

1 漂浮基空间机器人系统动力学模型

不失一般性，考虑做平面运动的漂浮基空间机器人(三杆)结构模型如图1所示.

图1 自由漂浮三杆空间机器人系统Fig.1 Free-floating space-based robot system

忽略微弱的重力梯度，空间机械臂系统为无外力作用的无根多刚体系统，其重力势能为0.将总动能T代入第二类拉格朗日方程，可以得到载体位置及姿态均不受控下欠驱动形式的系统动力学方程为

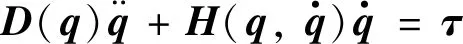
(1)

2 泰勒级数展开式在时延系统的应用

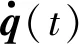
(2)

将含有时延的关节参数代入到三角函数中，并进行简化可得

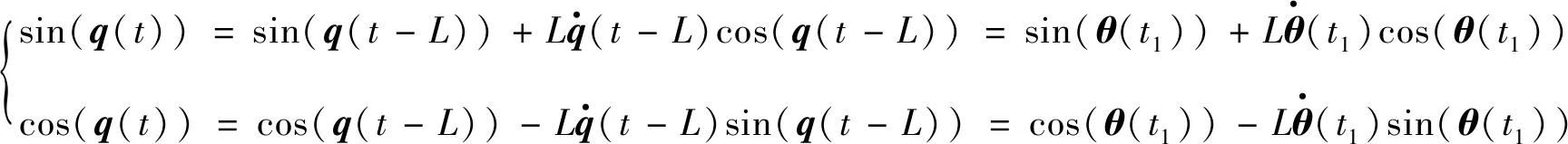
(3)

从上式可以看出，计算误差来源于对泰勒展开式高阶项的省略.

3 时延下基于泰勒级数展开的动力学模型

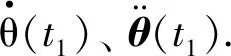
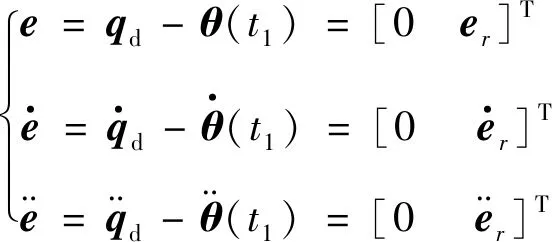
(4)

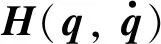
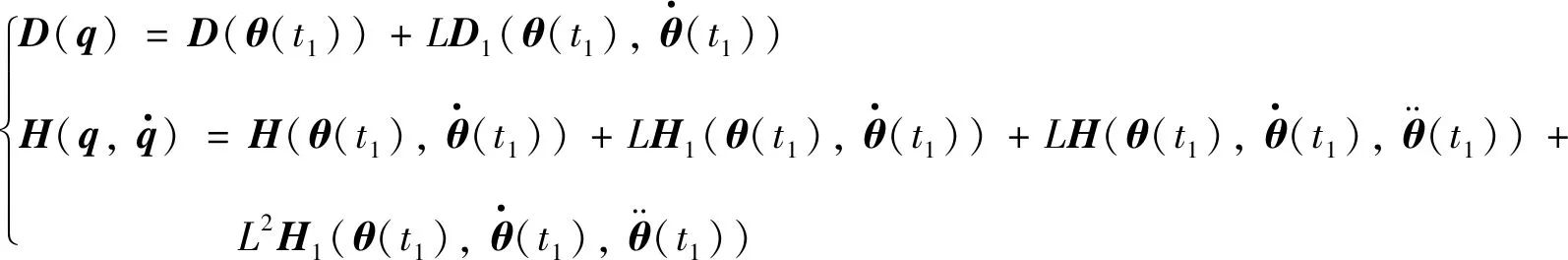
(5)

将式(5)代入动力学方程式(1)，可得到存在时延误差下的改进动力学方程为

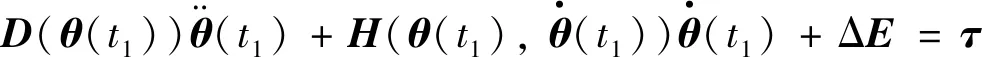
(6)

其中：ΔE为扩展后的剩余项.即系统存在的时延误差为

研究将用到以下假设.

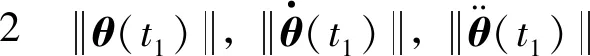
4 基于模糊递归的神经网络控制器设计

若不考虑时延误差，一般情况下对于动力学模型(1)，常规的计算力矩法反馈控制器τ可写为

(8)

其中:Kp、Kv为正定常值矩阵(增益因子).在没有时延误差的情况下，常规反馈控制器下的追踪误差逐渐收敛为0.若将常规控制器应用于改进的泰勒级数展开下的动力学模型，即将式(8)代入式(6)得

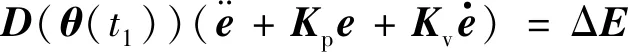
(9)

由于时延误差的存在，系统无法实现渐进稳定，需要引入补偿控制f(·)，使得在理想状况下有

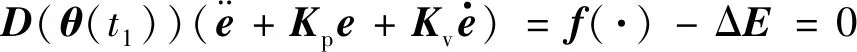
(10)

其中，时延项ΔE为未知的非线性函数.因此,这里引入基于模糊递归神经网络控制算法来补偿时延误差.

神经网络具有强大的非线性逼近能力及良好的在线学习能力，可以用其对非线性进行补偿；在此基础上引入模糊与归纳推理，将神经网络与模糊控制结合起来，构成具有推理归纳能力的模糊神经网络，提升控制品质.其综合性能更适用于非线性控制系统.所设计的模糊递归神经网络控制算法为三输入三输出的层网络结构，结构如图2所示.

图2 模糊递归结构Fig.2 Fuzzy recurrent neural structure

每一层的描述规则如下.

第一层接受输入变量.同时也作为第二层的输入变量.在姿态关节不受控前提下，设输入变量为误差函数s,有

(11)

第二层为隶属函数值计算阶段.采用高斯函数作为隶属函数，每一个节点都有一个隶属度函数,即

(12)

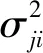
第三层为模糊推理层.由第二层得到的输出量通过规律连乘(模糊过程)得到第三层的输出量,且第三层上一时刻的输出量φjp经过bji的加权后反馈到第二层，构成了递归结构,即

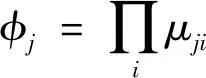
(13)

第四层为输出层.其输出表达式为

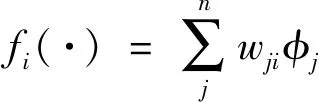
(14)

式中：fi为第四层输出量；wji为模糊推理层与输出层的连接权值，该值通过在线训练不断地调整φj第三层第j个节点的输出.将所有的输出结果进行整合，最终得到补偿控制的形式为

f(·)=WTΦ

(15)

其中:W为网络权值矩阵，Φ=[φ1φ2φ3…φn]T为最终的输出变量.

在一致估计理论和假设1的前提下，对于连续函数f(·)，对于任意给定的很小正数ε0，总是存在最优网络权值W*(f(·)的最佳逼近权值)，使得

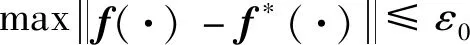
(16)

因此，定义逼近误差η=ΔE-f*(s)，并存在如下假设.

假设4 逼近误差η是有界的，即有

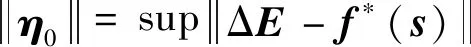
(17)

实际应用中理想补偿控制效果难以达到，因此设估计的补偿控制(实际输入控制)为

(18)

设理想网络权值与估计(实际)网络权值的误差为

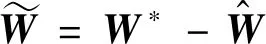
(19)

其网络权值自适应律在后续的李雅普诺夫证明中可得到.

综合式(8)、(18)，最终的控制器算法可写为

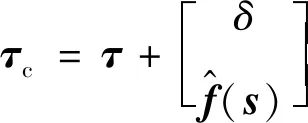
(20)

其中:δ是为保持等式右端载体姿态角项的输入控制力矩恒为0所设.

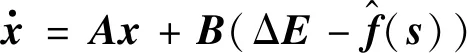
(21)

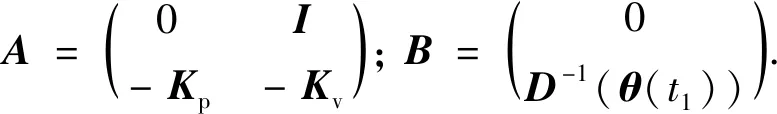
结合式定义逼近误差及式(19)，可得

因此最终状态方程可改写为

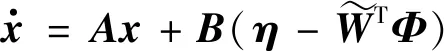
(22)

5 稳定性证明

对上述闭环系统，做如下稳定性分析，设计李雅普诺夫函数为

(23)

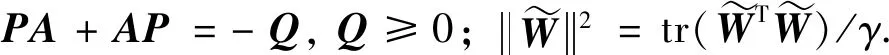
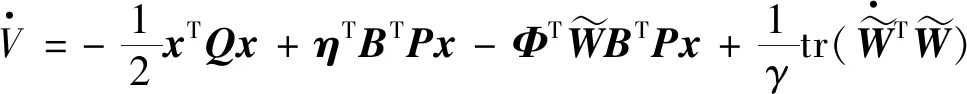
(25)

(26)

网络取值误差自适应律为

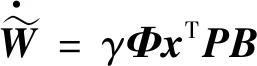
(27)

将式(27)代入到式(26)，可得

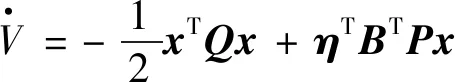
(28)

其中:λmin(Q)和λmax(P)分别为矩阵Q和P的最小特征值和最大特征值.

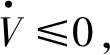
6 数值仿真算例

对图1所示的空间机器人系统进行数值仿真试验.设计参数如下：m0=40.00 kg，m1=2.00 kg，m2=1.00 kg，m3=2.50 kg；J0=34.17 kg·m2，J1=1.50 kg·m2，J2=1.50 kg·m2，J3=0.75 kg·m2；L0=1.50 m，L1=3.00 m，L2=3.00 m,L3=3.00 m;d1=1.50 m，d2=1.50 m，d3=1.50 m；隶属函数单元数为n=25;高斯基函数中心值c按间隔为0.5的均匀分布取值，基带宽度σ取值为1.2，其余值均为1；Q=diag(60,60,60，60,60,60);Kp=diag(25,25,25);Kv=diag(30,30,30).

利用本文所提出的控制手段进行数值仿真，其轨迹追踪结果如图3～5所示.为了突出本文所设计的控制方法(控制方法1)的优越性，将式(8)计算力矩法(控制方法2)和文献[14]所提出的常规RBF神经网络控制手段(控制方法3)与其进行比对，其轨迹误差e变化情况如图6～8所示.

图3 关节角1追踪结果Fig.3 Joint angle 1 tracking results

图4 关节角2追踪结果Fig.4 Joint angle 2 tracking results

图5 关节角3追踪结果 Fig.5 Joint angle 3 tracking results

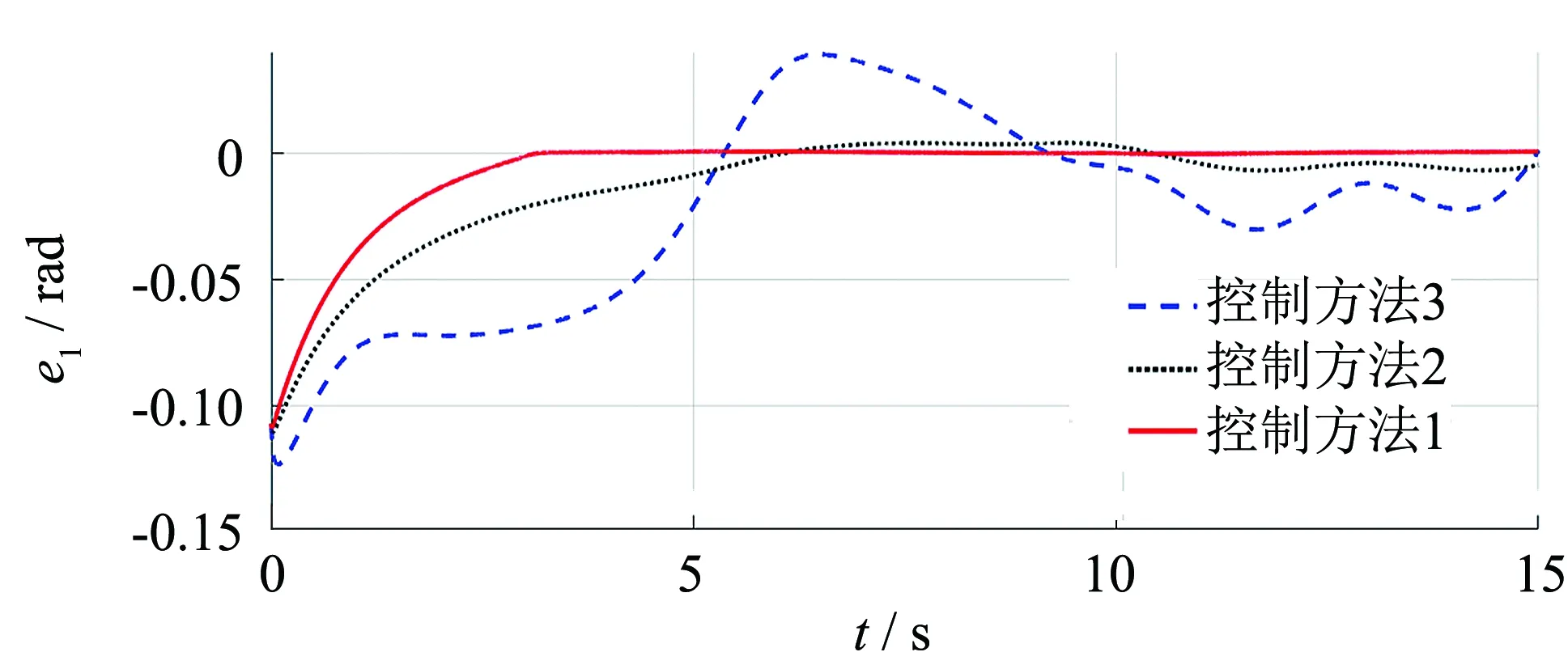
图6 关节角1追踪误差对比Fig.6 Comparison of joint angle 1 tracking error

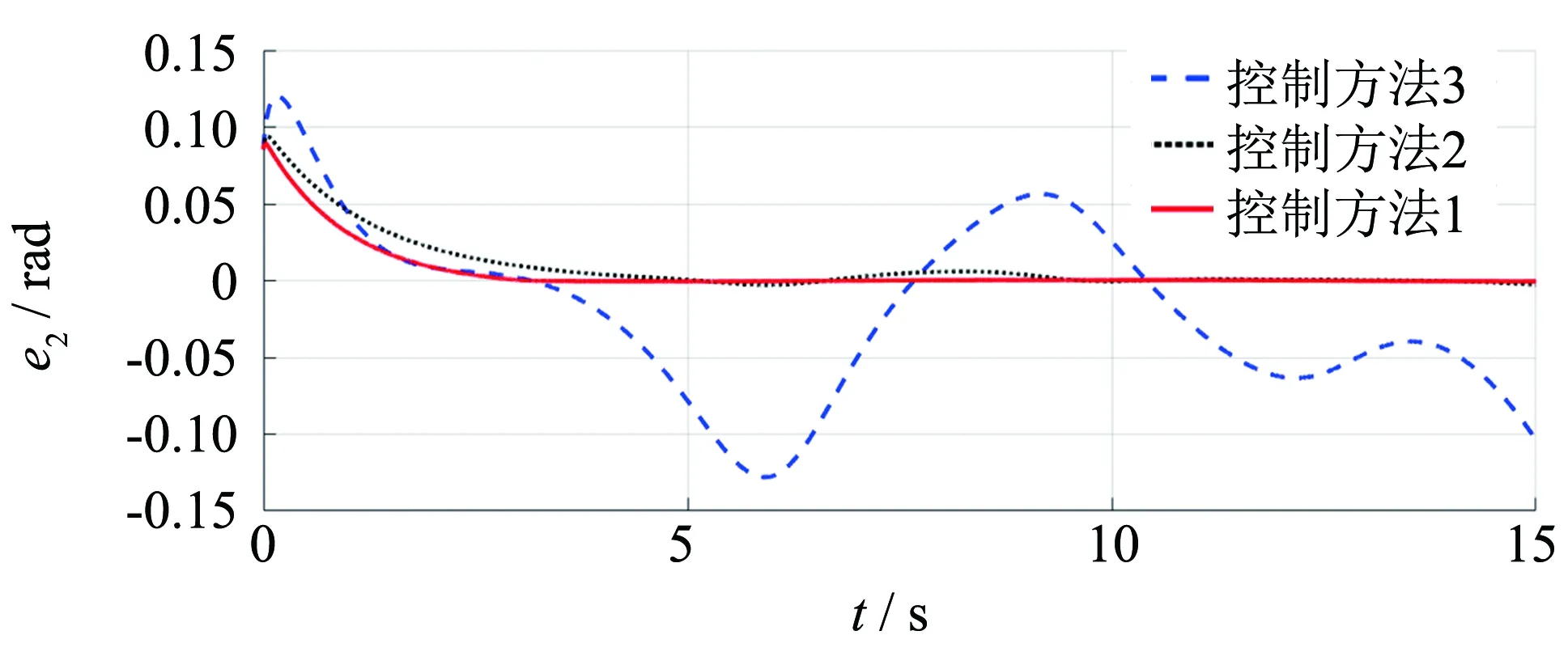
图7 关节角2追踪误差对比 Fig.7 Comparison of joint angle 2 tracking error

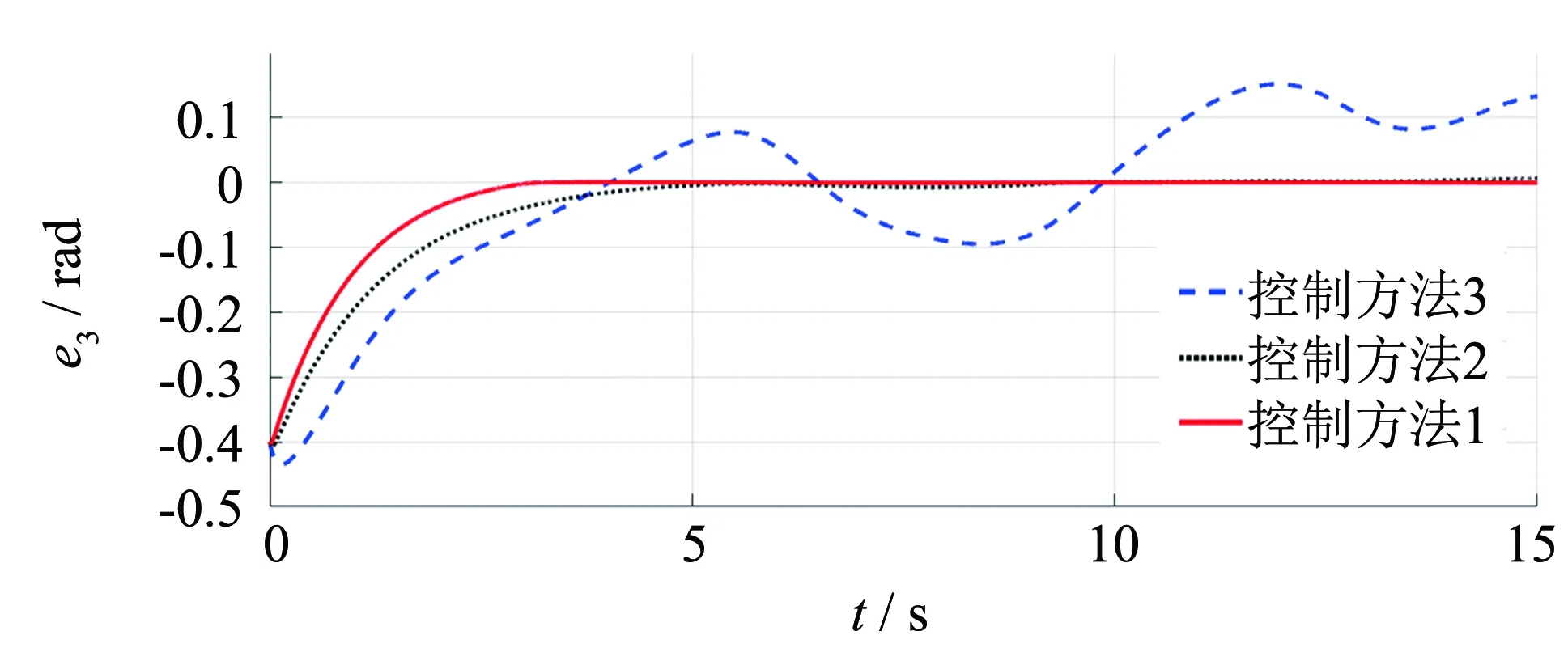
图8 关节角3追踪误差对比Fig.8 Comparison of joint angle 3 tracking error

从以上结果可以看到，用控制方法2根本无法保证系统的渐近稳定性；控制方法3可以有效追踪，但和本文所提出的控制方案1相比，收敛速度相对较慢，而且趋于稳定后会出现抖振.仿真结果说明，融合模糊递归的神经网络控制器既可以有效补偿时延误差，也可以提高收敛速度并减缓抖振现象，拥有更高的控制精度.

图9 关节角1追踪误差Fig.9 Joint angle 1 tracking error

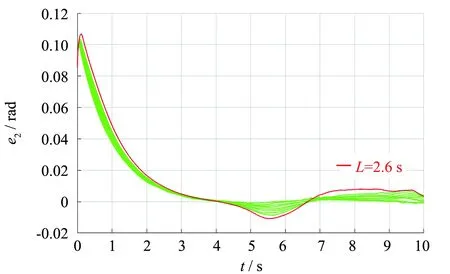
图10 关节角2追踪误差 Fig.10 Joint angle 2 tracking error

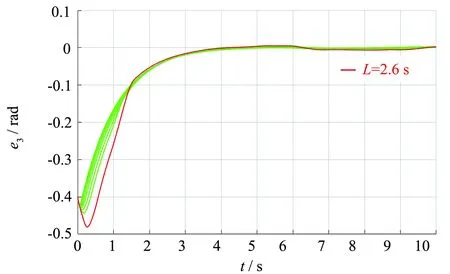
图11 关节角3追踪误差Fig.11 Joint angle 3 tracking error

结果显示，在L∈[0.1,2.6)范围内，误差在逐渐递增，当临近范围边缘，最大误差波动已经超过了0.01，虽然仍符合轨迹追踪效果，但是追踪精度已经不满足要求，这势必会影响控制品质，因此本文控制手段从理论上说延迟值在2.6 s以内都可以满足控制精度要求.

7 结语