变分自动编码器的潜变量空间解耦方法

曾青耀，郑茜颖，俞金玲

(福州大学物理与信息工程学院，福建 福州 350108)

0 引言

随着神经网络的不断发展，深度生成已经成为一项创建和操纵数据的强大工具.潜变量空间解耦这一研究方向大多是基于图像或音乐数据集的数据可控性研究.基于潜在表示的模型，例如文献[1]中变分自动编码器(variational auto-encoder,VAE)在潜变量空间解耦方面显示出卓越性能.

当前大多数无监督解耦方法都是基于VAE框架的变化.无监督方法试图解离数据中不同的变化因素，学习其表示形式.此类模型对单个基础变化因子的更改会导致学习到表示形式的单个因子发生更改.例如文献[2]中对潜在空间信息容量施加约束的β-VAE模型，文献[3]中最大化潜在编码子集和观测值之间互信息的生成式对抗网络模型(简称Info-GAN模型)，以及文献[4]中最大化潜在编码之间独立性潜在变量的解耦增强VAE模型(简称β-TCVAE模型)等.

监督方法是通过学习转换关系来控制属性的一类研究.文献[5]中属性正则化VAE模型(简称AR-VAE模型)试图沿着不同维度编码不同的数据属性.文献[6]中的乐器数字接口VAE模型(简称MIDI-VAE模型)将潜在空间分解为不同的部分，每个部分去对应特定的属性.文献[7]中的非对称多模式VAE模型(简称AM-VAE模型)则是通过学习潜变量空间和属性值之间的转换关系来控制数据属性.以上的监督学习方法也存在一些局限性，例如某些方法仅适用于某种类型的数据属性，或者模型需要通过独立改变属性来采样数据点等.同时，上述多数方法能够学习到在每一维度具体的、不相干意义的潜在表示,但其潜在表示的可解释性[8]仍不够强，其可控性和可拓展性较弱.然而在实现潜变量空间解耦的过程中，最重要的是让学习到的表征具备人类可理解的意义，让生成的数据属性更为可控.

本研究工作的主要包括以下4个方面：

1) 提出一种基于潜变量空间解耦的图像生成方法——自注意力属性VAE模型(简称TA-VAE模型)，通过改变编码结构和设计新颖的损失函数实现更优越的解耦性能；

2) 编码器阶段运用了自注意力机制[9]，使得本模型对长期依赖关系有着更强的捕捉能力，比起序列模型而言对层次结构信息能够进行更有效的表达；

3) 残差网络[10]使模型中信息的前后向传播更加顺畅，也让更深层的网络训练成为可能；

4) 标准数据集上的实验结果表明，本模型在训练过程中随着潜空间的变化，属性值变化更均匀，损失也更易于优化.

1 TA-VAE模型构建

提出一种自注意力机制下的潜变量空间解耦模型.在原始编码器的基础上使用了自注意力机制和残差网络来实现编码，在解耦方面也使用了新的损失来实现结构化潜在空间，从而沿着不同维度编码不同的数据属性.

1.1 编码器和解码器模型

1.1.1 编码器自注意力模型

本编码器结构模型如图1所示.在编码器上，运用了4层卷积层和1层线性层对图像数据进行特征映射和参数调整，能够有效地实现数据降维，并且高度保留图像特征.随后,将处理后的数据传入自注意力机制模型，捕捉数据特征的内部相关性.

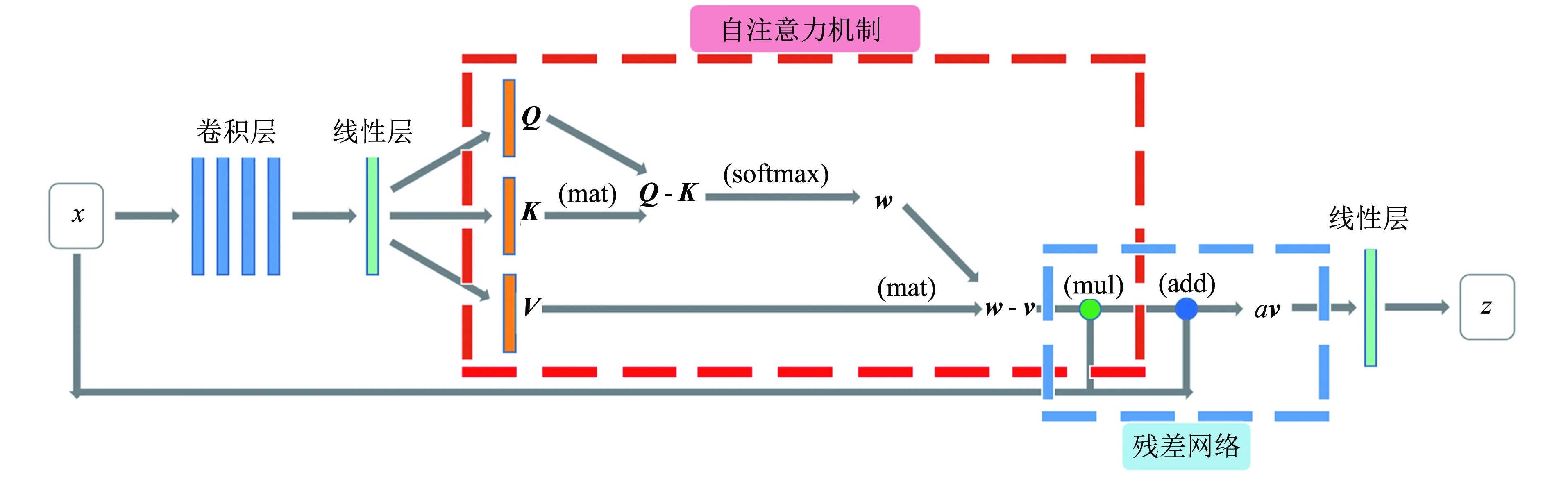
图1 编码器模型Fig.1 Encoder model

第一阶段，通过线性层将学到的数据分布式特征表示映射到样本标记空间，得到查询矩阵Q(query)、键矩阵K(key)和值矩阵V(value).

第二阶段，将Q和K网络的输出矩阵相乘，计算两者相关性，得到Q-K矩阵如下：

Similarity(Q,Ki)=Q·Ki

(1)

第三阶段，使用Softmax激活函数得到w，对第一阶段的原始分值进行归一化处理，将Q和K的缩放点积转化为注意力的相对测量.这里的计算结果ai即为V对应的权重系数，即：

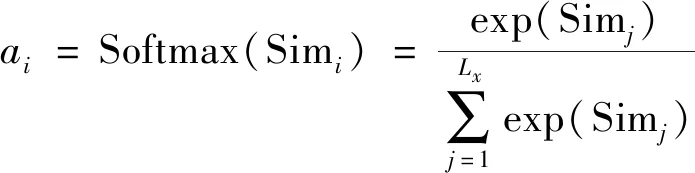
(2)

第四阶段，根据权重系数对V进行加权求和，将Softmax激活后的w与v矩阵相乘，得：

(3)

第五阶段，将得到的w-v矩阵和输入图像X进行元素级相乘，得到自注意力机制的输出w-v.总的自注意力机制计算公式为：

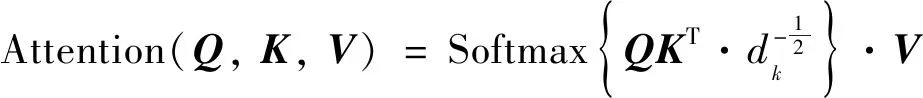
(4)

1.1.2 编码器残差网络

在得到QKV网络的输出后，将这一部分输出与输入图像相加，构成残差连接传到线性层，并从线性层输出模型所需的潜变量空间编码z.

在图1模型中的resnet部分，运用残差网络把输入图像直接映射到后面的网络层中，确保后面的网络层一定比前面包含更多的图像信息.这样能够避免网络退化现象，也能够避免可能存在的梯度消失问题.

1.1.3 解码器

本解码器结构模型如图2所示.在解码器阶段，使用三层线性层和四层转置卷积层将潜变量空间编码z解码，实现图像的重构.在每一个线性层和卷积层后都选择使用RELU函数进行激活.RELU函数在一定程度上增加了网络模型的稀疏性，使得模型提取出来的特征更具代表性.在相对小的运算量区间内成功提高网络的泛化性能.值得一提的是，在编码器和解码器阶段因参数量更少，较AR-VAE而言实现了更为轻量级的模型架构.

图2 解码器模型Fig.2 Decoder model

1.2 训练损失

提出一种新颖的潜变量空间解耦损失算法.在潜变量空间中采样z～p(z)，得到潜在空间上的先验分布.在高维数据空间采样x～pθ(x|z)，得到由θ参数化的解码器网络.本研究后验分布qφ(z|x)由编码器用参数φ近似.变分推理通过最大化证据下界(ELBO)来最小化近似后验和真实后验之间的KL散度，即：

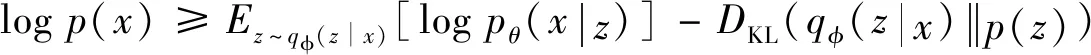
(5)

上式第一项，可被解释为最大化重构精度.第二项则是确保使用先验p(z)对潜在向量进行采样时生成真实样本.

综上，VAE的损失函数为：

LVAE(θ,φ)=Lrecons(θ,φ)+LKLD(θ,φ)

(6)

其中，重构损失为：

(7)

KL散度损失为：

(8)

接下来向VAE训练目标添加一项与属性值相关的损失：将一个潜在空间的潜在向量表示为z:{zk}，其中k∈[0,).本研究目标是能够沿着潜在空间维度r编码属性a.此时，当沿着r遍历，属性值a能够增加.

计算该损失有如下3个主要步骤.

1) 第一步，计算一个属性距离矩阵:

Da(i,j)=a(xi)-a(xj)

(9)

其中：i,j∈[0,m)；m为训练批量大小.

2) 第二步，为潜在向量正则化维度r计算类似距离矩阵：

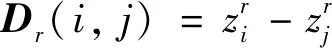
(10)

3)第三步，潜变量空间解耦损失为：

Lr,a=mean(exp(-tanh(δDr)·Da))

(11)

其中：δ是决定后验分布的可调超参数.

该潜变量空间解耦损失能够实现预计目标，即成功地沿着解耦维度r编码属性a，迫使解耦维度潜在编码与属性值具有单调关系.本研究中潜变量空间解耦损失变化均匀，且损失十分易于优化.该损失区间明显，在出现符合预期结果时loss变化剧烈，损失在(0，1)区间范围，出现不符合预期结果时损失会变为∞.

综上，总的损失函数为：

(12)

其中：β>1，鼓励潜在空间维度的独立性；γ为可调超参数，代表正则化强度；L为属性个数，l∈[0,).

该损失由三部分构成，分别是VAE重构损失、KLD散度损失和潜变量空间解耦损失.对属性距离矩阵Da和潜在空间维度距离矩阵Dr的定义部分地参考了AR-VAE.

2 实验与分析

2.1 实验环境设置

采用Python 3.7.4编程语言和Pytorch 1.3.0深度学习框架，设计了一系列定量实验，评估了包括解耦和重构上的若干指标.选取2-d sprites数据集[11]和Morpho-Mnist数据集[12]进行实验，并使用Adam优化器优化训练模型.

β-VAE作为一种非监督模型表现出与其他监督模型相当的性能，将其作为潜变量空间解耦领域的基线模型并与之对比.同时，也与使用属性正则化监督方法的AR-VAE模型进行对比.

本模型在图像数据集上进行测试，所以模型中运用到了卷积结构而不是循环结构.为了确保一致性，数据集采用相同的优化器、学习速率，并针对相同数量的Epochs进行训练.

1) 对于2-d sprites和Morpho-Mnist数据集，β-VAE、AR-VAE和TA-VAE模型都用了10种不同的随机初始化进行了训练.

2) 对于β-VAE模型,β设置为4.0进行训练.

3) 对于AR-VAE模型,γ设置为10.0，δ设置为1.0训练.

4) 对于TA-VAE模型,γ设置为10.0，δ设置为1.0训练.

2.2 数据集与属性

使用评估潜变量空间解耦的标准图像数据集2-d sprites和Morpho-Mnist.2-d sprites包含737 280个简单变化的二维形状.每一个二维形状具有五个属性，分别为：x轴位置、y轴位置、大小、方向、形状.

1)x轴位置：在[0,1]的区间范围均分，取32个不同的值.

2)y轴位置：在[0,1]的区间范围均分，取32个不同的值.

3) 大小：在[0.5,1]的区间范围均分，取6个不同的值.

4) 方向：在[0,2π]的区间范围均分，取40个不同的值.

5) 形状：有三种形状，方形、心形和椭圆形.

选取数据集总体的70%作为训练集(516 096张图片)，取20%作为验证集(147 456张图片)，取10%作为测试集(73 728张图片).

Morpho-Mnist包含70 000个手写MNIST数字，以及使用一种形态测量学获得的每个数字的复杂形态属性.这些属性包括面积、长度、厚度、倾斜度、宽度和高度.文献[12]中具体形态测量学方法如下.

因MNIST图像原始分辨率通常不足以支撑良好的形态学处理，并且直接在二值化图像上测量属性(例如长度、厚度等)可能不够准确并且量化严重.为了缓解这个问题并在测量中实现亚像素精度，Morpho-Mnist采取了以下处理步骤：1) 将图片放大；2) 二值化处理：将模糊的放大图像在其强度范围的一半进行阈值处理，以确保不会删除细小的或模糊的数字；3) 计算欧氏距离变换(EDT)：数字边界内的每个像素都包含到其最近边界点的距离；4) 提取骨架：检测EDT处理后的纹路，即检测与两个或多个边界点等距的点的轨迹；5) 运用提取出来的骨架信息为每个数字计算多种形态测量属性；6) 可选地对二值化图像应用扰动；7) 将二值化或扰动的图像缩小到原始分辨率.

2.3 实验结果

2.3.1 潜变量空间解耦指标

1) 可解释性(interpretability)[8].可解释性指标测量仅使用潜在空间的一个维度i来预测给定属性j的能力.通过对属性值j的每个测试样本点对应的结果概率对数求和，得到该属性的潜在空间可解释性得分.

2) 模块化(modularity)[13].它测量潜在空间的每个维度是否仅依赖于一个属性.如果编码维度能够理想模块化，它将与单个因子具有高互信息，而与其他因子具有零互信息.使用这个理想化案例的偏差来计算模块化分数.

3) 互信息间隙(mutual information gap,MIG)[4].它测量给定属性和与该属性共享最大互信息的潜在空间的顶部两个维度之间的互信息差异.

4) 分离属性可预测(spearman correlation coefficient,SCC)[14].SAP计算对特定属性的两个最佳预测维度之间的差值，即研究每个潜在空间维度是否只依赖于一个属性值.

5) 斯皮曼相关系数得分(spearman correlation coefficient,SCC)[15].其计算属性值和潜在空间的每个维度之间的斯皮曼相关系数的最大值.

2.3.2 指标对比分析

通过汇总所有属性的平均值，得到每个指标的得分.图3显示本模型TA-VAE与β-VAE、AR-VAE在2-d sprites以及Morpho-Mnist数据集上的解耦性能表现，所示分别是3个模型在5种解耦指标上的量化对比箱型图.图中的圆点表示不同的随机初始化情况下模型在该解耦指标上的分数.

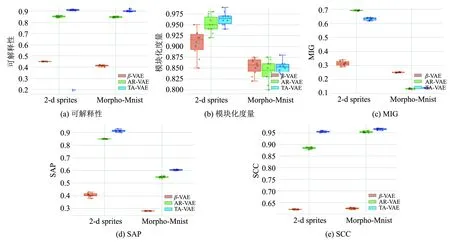
图 3 3个模型的指标对比Fig.3 Metrics of the three models

数据集2-d sprites上的模型解耦指标对比如表1所示.由表1数据对比分析可发现，本模型TA-VAE在5种指标的表现均远好于β-VAE.并且这种卓越的性能未来可能扩展到其他数据集，解耦不同领域和不同属性复杂程度的数据集.

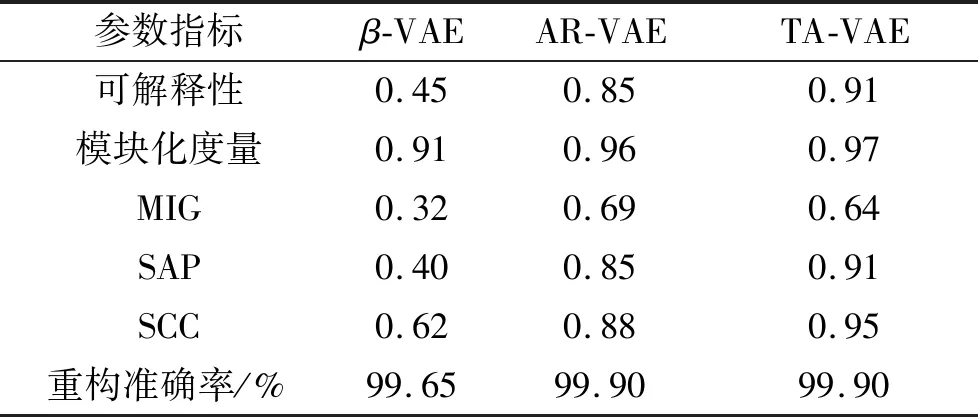
表1 数据集2-d sprites上模型解耦指标对比Tab.1 Comparison of metrics on the 2-d sprites

本模型TA-VAE与AR-VAE进行指标对比.

1) TA-VAE将可解释性指标从0.85提升到了0.91.这说明TA-VAE使用潜在空间的某一个维度预测给定数据属性的能力较AR-VAE更优.可解释性指标是潜变量空间解耦任务中最关键的指标.在可解释性上的大幅提升证明了TA-VAE模型优越的潜变量空间解耦能力.

2) 模块化度量指标上TA-VAE与AR-VAE持平.这可以通过观察所使用的指标计算方法进行解释.其计算过程中分数除以具有潜在维度的所有属性的互信息的最大值θi.这样就导致即使AR-VAE模型互信息的值相对较低，却也能够得到较高的模块化得分.

3) 互信息间隔(MIG)指标略低于AR-VAE.这表明潜变量空间中除了解耦属性的维度之外，还有其他维度与不同属性共享高度的互信息.

4) 分离属性可预测性(SAP)从0.85提升到0.91.这说明TA-VAE模型中每个潜变量空间维度更依赖于某一个属性值，属性在潜变量空间编码的分离效果上较AR-VAE更优.

5) 斯皮曼相关系数得分(SCC)从0.88提升到了0.95.这样的跃升说明TA-VAE模型某一属性的属性值与潜变量空间编码维度之间具有更为良好的单调关系.

数据集Morpho-Mnist上的模型解耦指标对比如表2所示.经表2数据对比分析可发现，TA-VAE在可解释性、SAP、SCC三种指标上均优于其他两个模型.但是在模块化指标上，TA-VAE与β-VAE、AR-VAE持平.在MIG指标上与AR-VAE持平，且低于β-VAE.

表2 数据集Morpho-Mnist上模型解耦指标对比Tab.2 Comparison of metrics on the Morpho-Mnist

从这里可以看出，Morpho-Mnist数据集上TA-VAE的表现也很好，但是2-d sprites数据集上的潜变量空间解耦度量通常会更高.出现这种结果的主要原因是2-d sprites是人工生成的数据集而Mnist是现实数据，2-d sprites数据属性复杂程度更低.

2.3.3 图像重构

2-d sprites数据集中有三种形状类别(正方形、心形和椭圆形).图4 (a)～(c)分别是3个模型在数据集上的属性遍历重构图像.这里展示心形图像进行对比.每一组图像内的不同列对应了沿着潜在空间维度对某种特定属性进行编码，从左到右的五列分别遍历了形状、大小、方向、x轴位置、y轴位置这5种属性.

图 4 2-d sprites的属性遍历图像Fig.4 Controlling different attributes of 2-d sprites

观察重构图像可以发现β-VAE重构效果最差.大小属性遍历的最后一个图像以及在心形旋转时都无法准确还原出心形.这说明β-VAE的潜变量空间解耦程度最低，难以实现很好的属性遍历效果.AR-VAE和TA-VAE在重构图像上明显更优.但AR-VAE在x轴遍历的最后一个图像上生成心形较TA-VAE更为模糊.

Morpho-Mnist数据集中有0～9共10种数字.图5 (a)～(c)分别列出3个模型在数据集上的属性遍历重构.这里展示数字7图像进行对比.每一组图像内的不同列对应了沿着潜在空间维度对某种特定属性进行编码，从左到右6列分别是面积、长度、厚度、斜度、宽度、高度的遍历.

图5 Morpho-Mnist的属性遍历图像Fig.5 Controlling different attributes of Morpho-Mnist

观察重构图像可以发现Morpho-Mnist数据集上3个模型的表现都不如2-d sprites数据集.β-VAE的重构图像最差，生成图像十分模糊.AR-VAE和TA-VAE在重构图像的清晰度以及属性遍历的完整度上明显更优.沿着潜变量空间的特定维度进行遍历，手写体数字的各种属性都在不断变大.但是在长度属性遍历中的最后一个图像上TA-VAE的长度较AR-VAE明显更长，厚度属性中TA-VAE的重构图像也更为清晰，厚度更大.

重构准确率是评估生成模型的重要指标.本实验测量了3种不同模型对2-d sprites图像,以及Morpho-Mnist手写体数据集的重构准确率，如图6所示.3个模型在2-d sprites数据集的重构准确率都很高.β-VAE为99.65%，AR-VAE和TA-VAE都高达99.90%.在Morpho-Mnist数据集，β-VAE为94.20%，AR-VAE为97.10%，TA-VAE为97.20%.虽然于目前的解耦任务而言重构准确率相对较高，并且提高解耦能力可能要以牺牲重构为代价.但本模型在解耦性能更好的情况下，重构准确率仍远高于β-VAE，并且高于AR-VAE.这也证明了本模型在潜变量空间解耦上的良好性能.

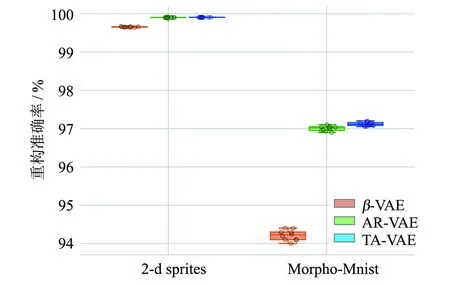
图6 3个模型的重构准确率对比Fig.6 Reconstruction metrics of the three models

3 结语

对编解码模型和训练损失进行新颖设计.通过构造沿着潜变量特定维度对数据属性进行编码的潜在空间，更好地实现潜变量空间解耦，生成图像数据.本模型在通用数据集2-d sprites和Morpho-Mnist上取得很好的解耦效果.通过客观指标对比，在保证重构精度的前提下，本模型在可解释性、分离属性可预测性(SAP)、斯皮曼相关系数得分(SCC)指标上取得提升效果，图像解耦性能优于β-VAE基线模型和AR-VAE先进方法.