典型柔顺常力模块结构参数评估与有限元优化

李玄，丁冰晓，李杨民

(1.吉首大学物理与机电工程学院，湖南 吉首 416000；2.香港理工大学工业与系统工程学系，香港 999077)

0 引言

常力机构是一种可在一定输入位移范围内，提供几乎恒定输出力的机构[1].因其力可调节特性，被广泛应用于超精密打磨和微操作等领域[2-4]，例如，使用常力机构设计的微夹钳，可用于对接触力敏感的柔软/易碎物体的夹持[5-6].传统用于操作力敏感物体的机电系统，通常配备了一系列传感器，通过闭环控制算法，输出作用力可以维持在一个特定的值[7-8].然而，精密的传感装置并不适合于复杂的环境和微尺度空间应用，同时力触觉传感器非常昂贵，控制装置也很复杂.鉴于这些考虑，部分学者提出了柔顺常力机构来解决以上问题[9-11].

柔顺机构利用柔性构件的弹性变形来实现力和运动传递，具有无需装配、无运动副间隙和高运动精度等优点，被广泛用于常力机构设计[12-14].为降低自动夹持过程中对果实的破坏，Miao等[15]设计了一种用于采摘机器人的恒力柔顺机构，其恒定夹持力约为8.03 N；为实现平稳接触未知对象，Meaders等[16]对一种近似恒力弹簧进行了优化，可用于不确定面的力接触；Liu等[17]设计了一种柔顺恒力系统，该系统具有较高的稳定性，可减缓一定的外界负载干扰；Chen等[18]设计了一种可避免抓取物损坏的夹钳，其恒定输出力为220 N，常力范围为440 μm；Pham等[19]设计了一种恒力双稳态机构，其恒定力大约为11 N，对应的输入范围为7～14 mm；Tolman等[20]设计了一种柔顺常力机构，通过伪刚体法和有限元法对其进行了建模与优化.

虽然常力机构的优势明显且发展迅猛，但对于大尺寸工作面和大接触力的场合，常力机构的应用通常受限于常力范围小和常力输出不足.针对此问题，优化机构性能显得十分迫切，同时这也是每个结构的需求.多数优化方法较为复杂，如粒子群算法(PSO)的编码过程较复杂，且具有易陷入局部最优、无法有效解决组合优化等缺点[21].有限元优化法应用较少，但其操作简单、通用性强，且具有可进行响应面分析、求出参数对结果的灵敏度并推荐最优的参数组合等优点[22].综上，本研究运用有限元优化法对常力机构的性能进行优化.首先，基于Z型梁和双稳态梁并联的结构，提出一种常力柔顺机构；其次，通过推导常力机构的力-位移表达式，得到与机构性能相关的结构参数；然后，使用有限元仿真，将所求结果与理论分析进行对比，并经由Matlab计算，得出两种梁的主要结构参数对机构常力特性的影响关系；最后，选择待优化的参数组合，运用有限元优化法求解其最优值，以获得机构的最优性能.

1 常力模块设计与分析

不同于传统机构，零刚度机构不满足胡克定律，可通过正负刚度机构组合来获得.当前，正刚度梁多采用柔性直梁，但柔性直梁存在应力硬化现象，即随着输入位移的增大，其刚度会相应增大，反过来拉伸应力的增大，导致弯曲刚度的增大.同时，该机构刚度非线性特性明显，不利于获得大范围的常力输出.为了弥补柔性直梁的不足，Z型梁被设计用于正刚度机构，两者的力-位移特性如图1所示.可以看出，随着输入位移的增大，Z型梁相较于传统柔性直梁具有更好的线性正刚度特性，能提供更大的位移行程，以便与负刚度中和形成零刚度.

图1 两种柔性梁的力-位移特性对比Fig.1 Comparison of the force-displacement characteristics of straight beam and Z type beam

1.1 模块设计

为使分析与优化方法更具典型性与通用性，选择较具代表性的Z型折叠梁与双稳态梁组合的常力模块作为研究对象，如图2所示.该模块采用正负刚度组合原理实现常力输出特性，具有无摩擦、高输出精度和结构简单等优点.整体结构由2根Z型梁和4根双稳态梁组成，为提高机构整体的刚度和紧凑性，双侧各由两根双稳态梁并联组成.由于双稳态梁的屈曲特性，机构会在一定输入位移范围内表现出零刚度特性，使得机构末端输出恒力.

图2 常力模块Fig.2 Designed constant force module

1.2 正刚度分析

通过分析两种梁的力学特性，可了解机构的常力特性，同时可得到影响其力学性能的相关结构参数，

为参数的评估与有限元优化做铺垫.机构的Z型梁由3段叶片柔性梁组成，其受力变形如图3所示.当输出力F1时，单个叶片梁因受力而产生弯曲变形.图中，l1、l2、l3分别为各叶片梁的长度；θ1、θ2、θ3分别为各叶片梁的变形角度；d为梁的厚度；b为梁的宽度；M1为梁固定端所受力矩.

图3 Z型梁受力形变图Fig.3 Deformation of the Z-shaped beam

处于悬臂状态的叶片梁，其悬臂端受到力F作用时，其受力平衡可表示为

(1)

(2)

式中：δx为自由端的输出位移；M为叶片梁固定端所受力矩；l为叶片梁的长度；E为材料的杨氏模量；I为梁的惯性矩.依据式(1)和(2)，可得

3．不同病理分级NEN的SCGN、CgA阳性表达： G1、G2、G3级NEN中SCGN阳性表达率的差异有统计学意义(H=8.472，P=0.018，表2)，其中G1与G2级、G2与G3级NEN的SCGN阳性率差异无统计学意义，而G3级NEN的SCGN表达率显著低于G1级(秩均值：13.67比24.18)，差异具有统计学意义(Z=-2.506，P<0.017)。不同病理分级NEN的CgA表达差异无统计学意义。

(3)

由于Z型梁由3段叶片梁组成，所以其输出力为

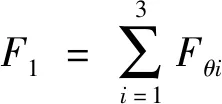
(4)

式中：Fθi为Z型梁中单个叶片梁的输出力，i=1,2,3.依据式(1)～(3)，进一步得

(5)

依据图3中Z型梁变形后的几何关系，可得

(6)

结合式(6)，可通过式(4)和(5)，求出Z型梁的力-位移关系表达式.

1.3 负刚度分析

负刚度结构采用具有屈曲特性的双稳态梁，建模如图4所示.当双稳态梁受到力F2作用时，会出现屈曲变形.图中，L、d分别为双稳态梁的长度和宽度；θ为梁相对于垂直固定面平面的倾斜角度；ε为倾斜导向梁受到F2作用而输出的位移.

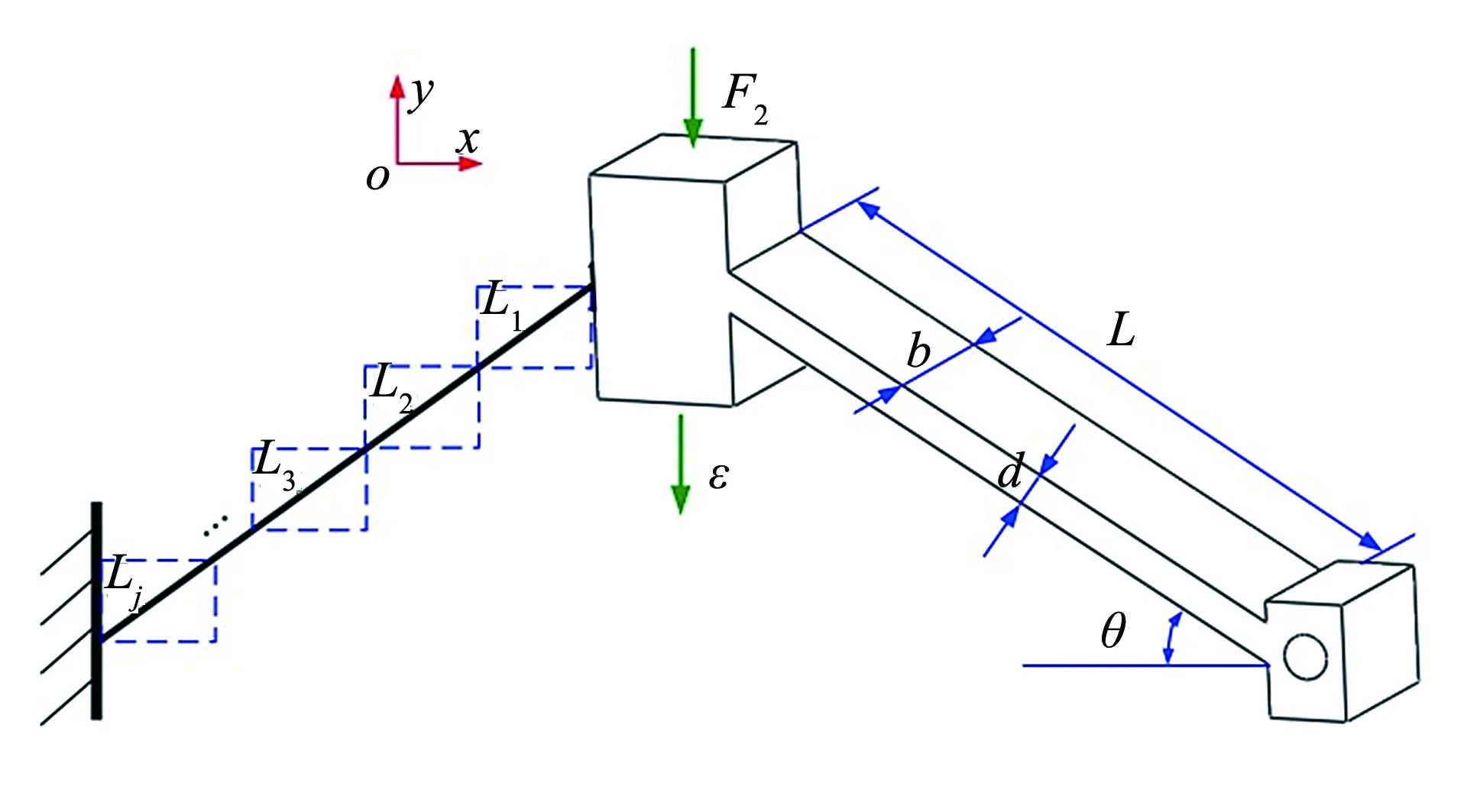
图4 双稳态梁建模Fig.4 Bi-stable beam model

其中导向梁第j个临界点的屈曲力[23]为

(7)

可得到双稳态梁的负刚度表达式为

(8)

依据式(7)和(8)，双稳态梁的力-位移关系式为

(9)

式中：S=bd为梁的横截面积.当θ为零，利用式(9)可求出传统直梁的力-位移关系式.

依据式(4)和(9)，可得常力机构整体的力-位移表达式

(10)

2 仿真结果与分析

为验证理论分析的正确性，利用Workbench进行仿真验证.运用Matlab进行相关参数对机构常力特性的影响分析.

2.1 有限元仿真

机构采用的材料为具有较高弹性的ABSplus-P340.其密度为1 040 kg·m-3，杨氏模量E=2.2 GPa，泊松比μ=0.394，常力机构的主要参数如表1所示.其中，dz、db分别为Z型梁和双稳态梁的宽度.

将机构的三维模型导入有限元软件，建立有限元模型，在所有定位孔的内圆柱面施加固定约束，在提前建立的加载节点进行位移加载，理论与仿真的力-位移曲线如图5所示.由图5可知，理论与仿真结果较为吻合，常力输出部分较为贴近.在输入位移1.2 mm左右常力机构曲线开始变得平整，常力输出对应的位移区间大约是[1.2,2.5] mm.恒定输出力大约为18 N，恒力变化范围大致为[16.8,17.5] N.

图5 理论与仿真结果对比Fig.5 Comparison of analytical and simulation results

2.2 参数影响分析

常力机构输出恒力的大小、稳定性及其输出位移范围与机构中各结构参数有关.因此，需评估机构中部分参数对机构力-位移输出特性的影响，同时为结构参数的进一步优化奠定基础.

由式(10)和表1可知，模块的常力特性主要受到Z型梁和双稳态梁各结构参数的影响.分析某一参数对常力特性的影响时，其他参数应保持不变.选取的Z型梁参数l2、dz变化时，机构的力-位移变化曲线如图6所示.选取的双稳态梁参数θ、db变化时，机构的力-位移变化曲线如图7所示.

图6 结构参数对Z型梁力学性能的影响Fig.6 Effect of architectural parameters on the performance of the Z-shaped beam

图7 结构参数对双稳态梁力学性能的影响Fig.7 Effect of architectural parameters on the performance of the bi-stable beam

分析图6、图7，可得出：

1) 由图6(a)可知，随着l2的增大，正刚度值减小，常力曲线趋向于负刚度曲线.其值在[8,12] mm区间时，正刚度与负刚度中和形成常力.

2) 由图6(b)可知，随着dz的增大，正刚度增大，常力曲线趋向于正刚度曲线，其值在区间[0.8,1.2] mm内时，正刚度与负刚度中和形成常力.

3) 由图7(a)可知，随着θ的增大，双稳态梁的屈曲点向位移更大的位置移动，且相应的输出力增大.负刚度曲线的陡峭程度变大，负刚度区域随之增大.常力范围增大，整体向位移更大的方向移动.

4) 由图7(b)可知，随着db的增大,屈曲点位置几乎不变，但输出力会增大，负刚度曲线越陡，常力范围越小，常力曲线趋向于负刚度曲线.

综上，4个结构参数中dz和θ对机构的力学性能影响最大.因此，有必要选定上述两参数参与优化，以获得机构的最优性能.

3 优化分析

由节2.2可知，通过改变结构参数的大小，机构可获得不同的力-位移输出特性.因此，在一定的参数变化范围内，通过优化参数，选择参数的最佳值，可实现机构的最优化设计.机构的优化分析可利用有限元软件ANSYS Workbench完成.该方法采用多目标遗传算法，可求解出由不同优化参数和输出参数所组成的设计点，推荐最优的优化参数组合；并可获得优化参数对输出结果的影响关系.本研究选取5个独立的结构参数作为优化参数，其上限、下限值如表2所示.

表2 优化参数变化范围Tab.2 Range variation of optimized parameters

机构的优化目标为在选定的参数变化范围内，获得最大的常力范围和大的常力值.为便于机构的优化分析，定义恒力比例因子(constant force ratio factor,CSRF) 这个物理量作为输出参数，其值为常力输出对应的位移区间大小与总输出位移的乘积.由定义可知，当恒力比例因子增大，常力范围会相应增大.结合机构的实际工作情况，另选机构的总变形最大值(total deformation maximum,TDM)和等效应力最大值(equivalent stress maximum,ESM)作为输出参数.优化的效果应使恒力比例因子和总变形最大值达到最大，等效应力最大值达到最小.

为实现优化目标，系统会计算出足够的设计点作为样本参考.采集的样本设计点越多，整体计算的误差值越小，优化的精确度越高.此次优化一共采集了1 004个设计点，样本如图8所示.图中上下两条水平边界线表示优化参数和输出参数的最大、最小值；每一条曲线对应一个设计点，表示5个优化参数的取值与对应的输出结果.图9为输出参数的响应面预测值与计算观察值之间的拟合关系，由图9可知，ESM相较于TDM和CSRF展现出更好的线性拟合度，精确度较高.

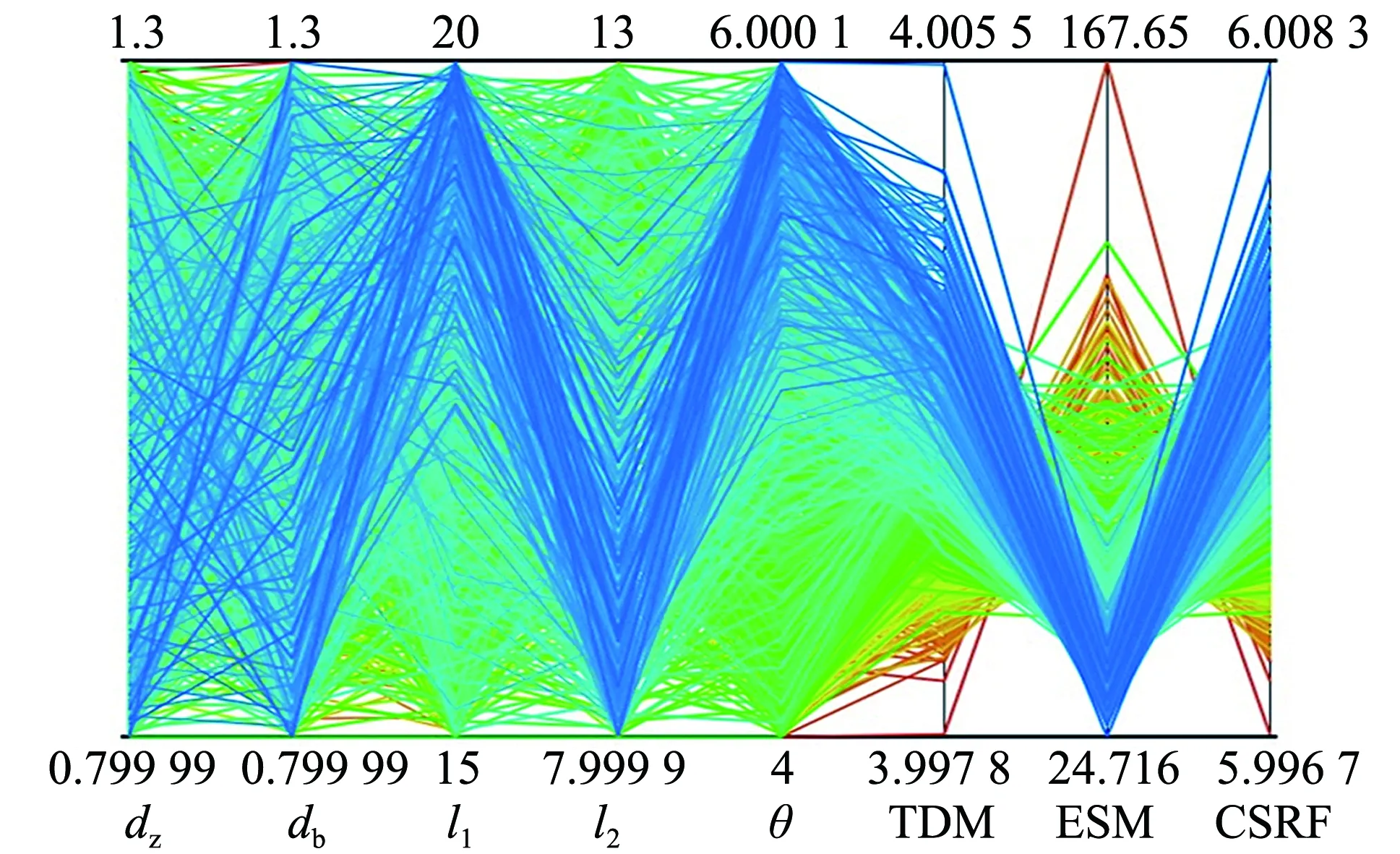
图8 设计点采样图Fig.8 Sampling of design point

图9 预测值与观察值拟合度Fig.9 Fitting of the predicted value to the observed value

通过响应面分析，可得到优化参数对输出参数的关系.针对优化目标，主要分析不同优化参数对CSRF的关系，如图10所示.选取的4个优化参数对ESM的关系如图11所示.依据图10、11，可得出：

图11 结构参数与ESM的关系Fig.11 Relationship between architectural parameters and ESM

1) 随着l1、db和θ的增大，CSRF相应呈不同幅度的增大，3个参数与CSRF为正比拟合关系；随着l2和dz的增大，CSRF相应呈不同幅度的减小，两个参数与CSRF为反比拟合关系.根据CSRF的定义，各优化参数对TDM的关系与CSRF一致.

2) 随着l2、db和θ的增大，ESM相应呈不同幅度的增大，3个参数与ESM为正比拟合关系；随着l1的增大，ESM相应呈不同幅度的减小，该参数与ESM为反比拟合关系.

由响应面分析可知，各优化参数对输出参数的影响不尽相同.此外，其影响程度也不同，即个别优化参数对输出参数的影响大于其他参数.优化参数对输出参数的灵敏度如图12所示，由图12可知，单个优化参数对CSRF和TDM的影响程度相同，θ对两输出参数的影响程度最大，其次为l1和dz，最后为db和l2；各优化参数对ESM的影响程度中，l1和l2对其影响程度最大，其次为db和θ，最后为dz.

图12 优化参数对输出参数的灵敏度Fig.12 Sensitivity of the optimized parameters to the output parameters

在已知各优化参数对输出参数的影响关系及灵敏度的条件下，需根据优化目标对优化参数进行优化.在ANSYS优化模块中，多目标遗传算法可在优化参数与输出参数生成的响应面上，寻找最佳的优化结果待选点.本研究最终选择的5个优化参数的最优取值如表3所示.

表3 优化参数的最优值Tab.3 Obtained optimized parameters

运用SolidWorks建模，将5个参数的最优值替换原值，导入Workbench进行仿真求解.优化的常力机构的力-位移输出特性与优化前进行对比，结果如图13所示.优化的常力机构仍具有常力特性.在输入位移2.0 mm左右,力-位移曲线开始变得平整，常力输出对应的位移区间大约是[2.0,4.5] mm.恒定输出力大约为68.5 N，恒力变化范围大致为[65.8,73.4] N.相较于未优化的常力机构，常力输出区间增加了1.2 mm，常力值增加了50.5 N.因此，验证了该优化方法的有效性与可靠性.

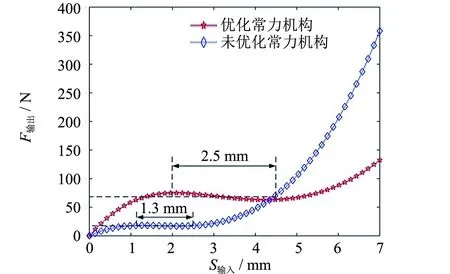
图13 优化前后力-位移曲线对比Fig.13 Comparison of force-displacement curves between original and optimized module

4 结语

本研究提出面向正负刚度组合的常力机构参数评估与有限元优化方法，通过建立Z型梁与双稳态梁的数学模型，得出机构结构参数和常力输出特性的关系.运用Matlab仿真，评估各结构参数对机构性能的影响，选择5个结构参数作为优化变量，定义CSRF、TDM和ESM作为输出参数，使用有限元优化法进行优化求解.基于优化过程中的响应面分析与参数敏感度分析，得出了θ对机构常力特性的影响较大的结论.优化的机构常力输出的位移区间为[2.0,4.5] mm，恒定输出力为68.5 N，其恒力变化范围为[65.8,73.4] N.研究成果可为常力机构的参数优化和拓展应用等方面的研究起到积极的推动作用.