结构保持图拉普拉斯正则的快速图像修复

曾勋勋，陈飞

(1.福州大学数学与统计学院，福建 福州 350108;2.福州大学计算机与大数据学院，福建 福州 350108)

0 引言

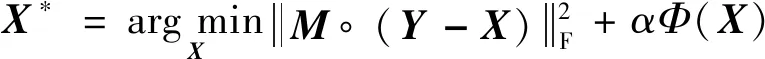
(1)

最近，图拉普拉斯作为图像的正则先验受到极大的关注[16-17]，其假设原始的图像关于一个给定的图是分片平滑.这种基于图的表达跟传统的方法相比具有更加紧、精确和结构自适应等优点[16].早期图拉普拉斯正则[18]是采用固定的图拉普拉斯矩阵提升信号的分片平滑性.之后，考虑到信号的变化对所构建的图有辅助作用，信号依赖的图拉普拉斯正则(SDGLR)[17]被提出，其中拉普拉斯矩阵的边权重的构建是依赖于图像像素的灰度值差，即拉普拉斯矩阵可以看作是信号的函数.最近，特征图拉普拉斯正则[19]被提出并应用于提升点云数据的分片平滑性质.对于图像修复，梯度有助于结构保持，可以促进待修复区域与周围图像信息的一致性.然而，如何有效将梯度特征融合至图拉普拉斯矩阵是一个关键问题.

将梯度作为图像结构保持的重要特征，利用图拉普拉斯矩阵提升梯度域图像的分片平滑性.首先将图像看作图信号，构建图拉普拉斯矩阵，然后对水平梯度图像和垂直梯度图像进行图拉普拉斯正则，接着图像修复模型可以转化为线性方程组，最后通过共轭梯度法快速求解.

1 图的构建

对于二维图像X∈RM×N，首先按列排成一维长向量x,x=vec(X)∈RMN×1,其中：vec(·)表示向量化操作算子.接着，定义一个包含MN个节点(图像像素)的图，图中每个节点包含两个信息：像素位置li和像素的灰度值xi,i∈{1,2,…,MN}.wi,j表示节点i和节点j之间的边权重,其定义用高斯核函数表示为：

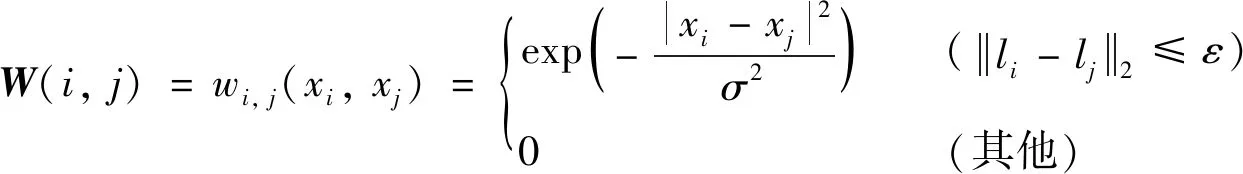
(2)

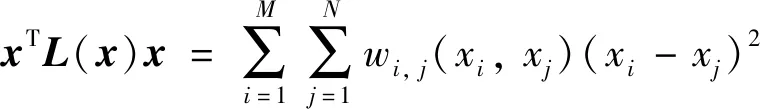
(3)

2 结构保持图拉普拉斯正则

对于图像修复来说，利用周围信息向待修复区域传播时，通过引入图像梯度信息，保持图像结构特征是一种有效方法.给定二维图像X∈RM×N，其水平梯度图像和垂直梯度图像可通过逐行和逐列计算得到.为了使得到的水平梯度图像与垂直梯度图像维数一致，将边界梯度值置0.以水平梯度图像为例，对于任意k∈{1,2,…,M},l∈{1,2,…,N-1}，定义Gh(k,l)=X(k,l+1)-X(k,l)且Gh(k,N)=0.那么水平梯度图像Gh∈RM×N可以转换为一维形式，gh=vec(Gh)∈RMN×1，其矩阵表达方式为：gh=Fhx.其中：Fh∈RMN×MN为水平梯度算子.类似地，对任意l∈{1,2,…,N}，垂直方向的梯度图像定义为：Gv(k,l)=X(k+1,l)-X(k,l),k∈{1,2,…,M-1}且Gv(M,l)=0,那么，有：gv=Fvx.其中，Fv∈RMN×MN为垂直梯度算子.

对于图像X，在点(k,l)处的梯度(Gh(k,l),Gv(k,l))指明了图像灰度值最大的增长方向.如果点(k,l)处在图像的边缘位置，那么其切线方向将近似垂直于该点的梯度方向(见图1).因此在周围已知区域向待修复区域信息传播的过程中，通过梯度方向保持一致可以保护图像的边缘结构.为了提升梯度域图像的近似分片平滑性，对图像X的水平梯度图像Gh和垂直梯度图像Gv，提出结构保持的图拉普拉斯正则项：

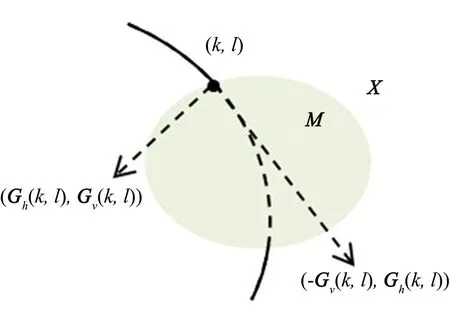
图1 图像X上边缘点(k,l)处梯度方向Fig.1 The gradient direction of edge point(k,l) on image X

(4)

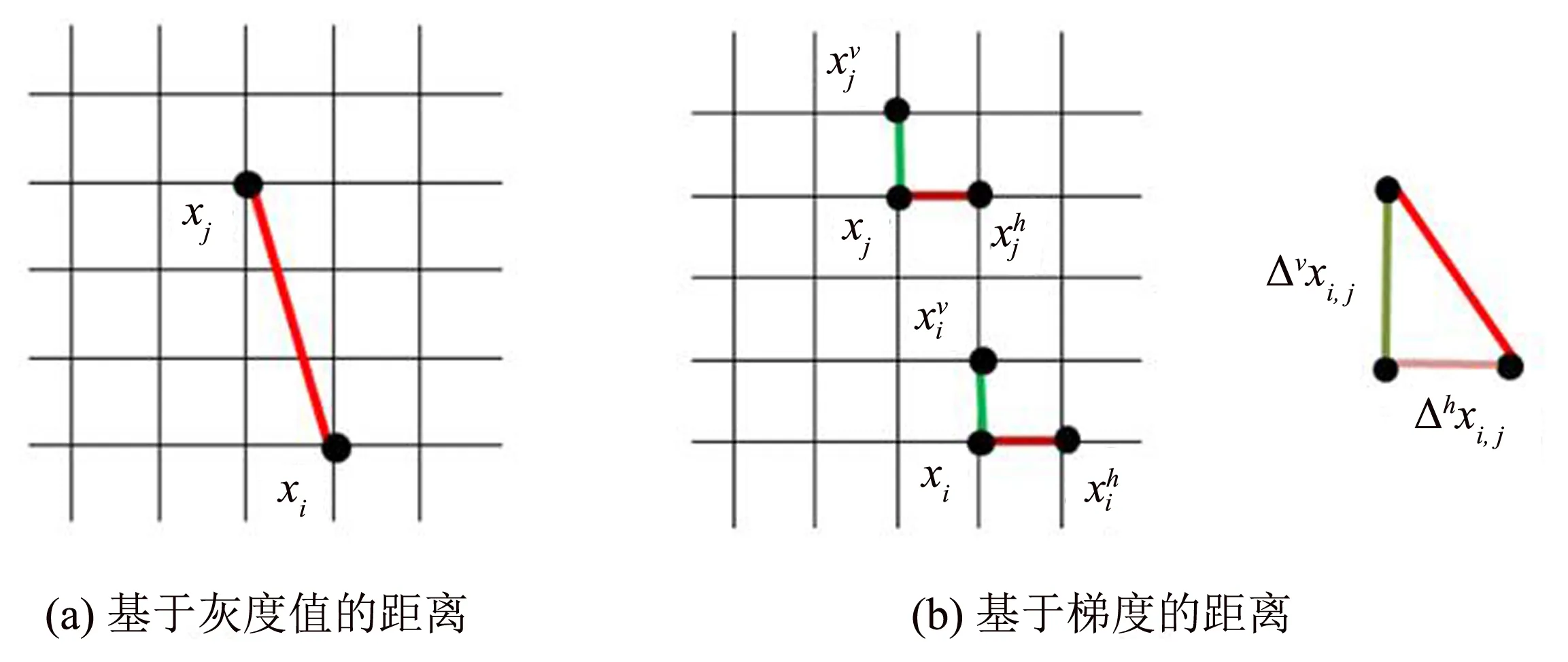
图2 两种距离的比较说明Fig.2 Comparison illustration of two distances

接下来，从连续域上证明任何分片平面图像f是正则函数Φ的全局最小值.假设Ω是图像支撑域,Ωi(i=1,2,…,T)是Ω的一个划分.那么，分片平面图像可以定义为：

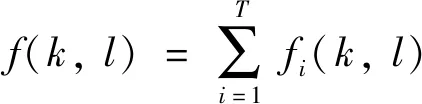
(5)

其中，

(6)

这里，组合图像f(k,l)是连续的.注意到任何两个连接的fi(k,l)和fj(k,l)必须在不同平面上，否则可以合并为一个平面.定义∂Ωi为划分区域Ωi的边缘，那么Ωi-∂Ωi是Ωi的内部.显然有

∇fi(k,l)=常数 ((k,l)∈(Ωi-∂Ωi))

(7)

那么，对于i=1,2,…,T,有：

∇2fi(k,l)=0 ((k,l)∈(Ωi-∂Ωi))

(8)

则可以得到：

∇2f(k,l)=0 ((k,l)∈(Ω-∂Ω))

(9)

对于任意两个相邻的不同平面fi和fj上，由于梯度在边界∂Ω处是不连续的，故∇fi≠∇fj.因此，∇2f(k,l)=∞,(k,l)∈∂Ω.如果权函数w(k,l)是通过高斯核函数计算得到，那么有w(k,l)=exp(-∞)=0.所以，下式成立.有：

w(k,l)(∇fi(k,l)-∇fj(k,l))=0 (∀(k,l)∈Ω)

(10)

因此，分片平面图像满足：

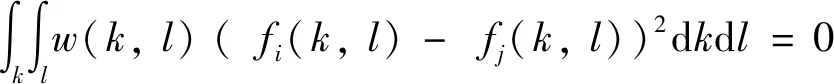
(11)

那么，Φ(f)=0.对于一个分片平面图像x及其图定义权重wi,j，在不同平面的交界处wi,j≈0，有

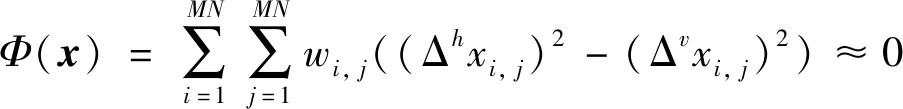
(12)

3 图像修复

给定一张退化的一维图像y∈RMN×1，引入结构保持的图拉普拉斯正则项式(4)，从中恢复潜在的真实图像x，可以用模型表示为：

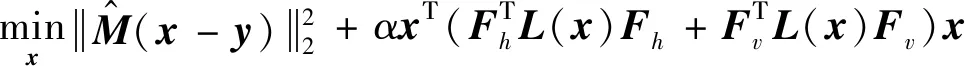
(13)

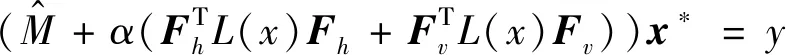
(14)

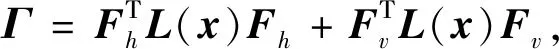
为了评价所提出算法的图像复原效果，定理1给出了图像修复误差上界，说明了该上界与矩阵Γ的特征值紧密相关.针对分片平面图像x，与传统的拉普拉斯矩阵相比，定理2给出了特征值之间的关系，从而保证所提出的解与图拉普拉斯正则得到的解相比可以得到更小的上界.

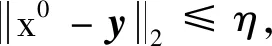
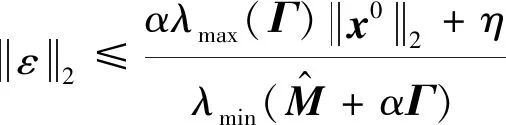
(15)

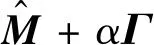
证毕.

证明 假设ρ(xi)是xi所在的平面，wi,j是指用相同的高斯核函数定义的xi与xj相似性权重，那么有：

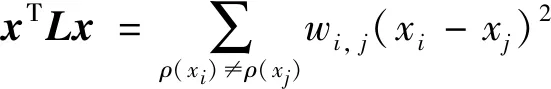
(16)

以4邻域4连接图为例，考虑xi与xj所有可能的平面，都有：

因此，Γ≥L.通过Rayleigh引理[20],有：

(17)

证毕.

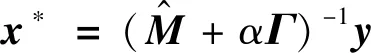
4 实验结果与分析

本研究算法在设置权重矩阵式(2)时，ε采用4邻域构建4连接图，核函数σ设置为0.58.图像修复算法中正则项参数α设置为0.01.为了评价图像复原的质量，引入PSNR (峰值信噪比)和SSIM(结构相似性)作为衡量指标：

为了验证所提出的算法，首先与图拉普拉斯正则(SDGLR)[17]做比较.图3给出了两组实验结果，SDGLR容易过于平滑，且与周围的纹理不一致，块状明显.本研究提出的结构保持图拉普拉斯正则化方法，可以更好地保持图像纹理信息，使得修复后的图像更加自然.

图3 视觉与PSNR比较Fig.3 Visual and PSNR comparison

为了综合比较所提出的结构保持图拉普拉斯正则器，比较了当前主流的图像修复算法，包括SDGLR、EPLL[22]、CSC[3]、IRCNN[23]、IDBP[2]、GSC[24].注意到IRCNN是基于深度学习的方法.以12张常见图像为测试数据[25]，随机丢失90%以上像素，采用不同方法重建图像，其修复后的的平均PSNR和SSIM列在表1.

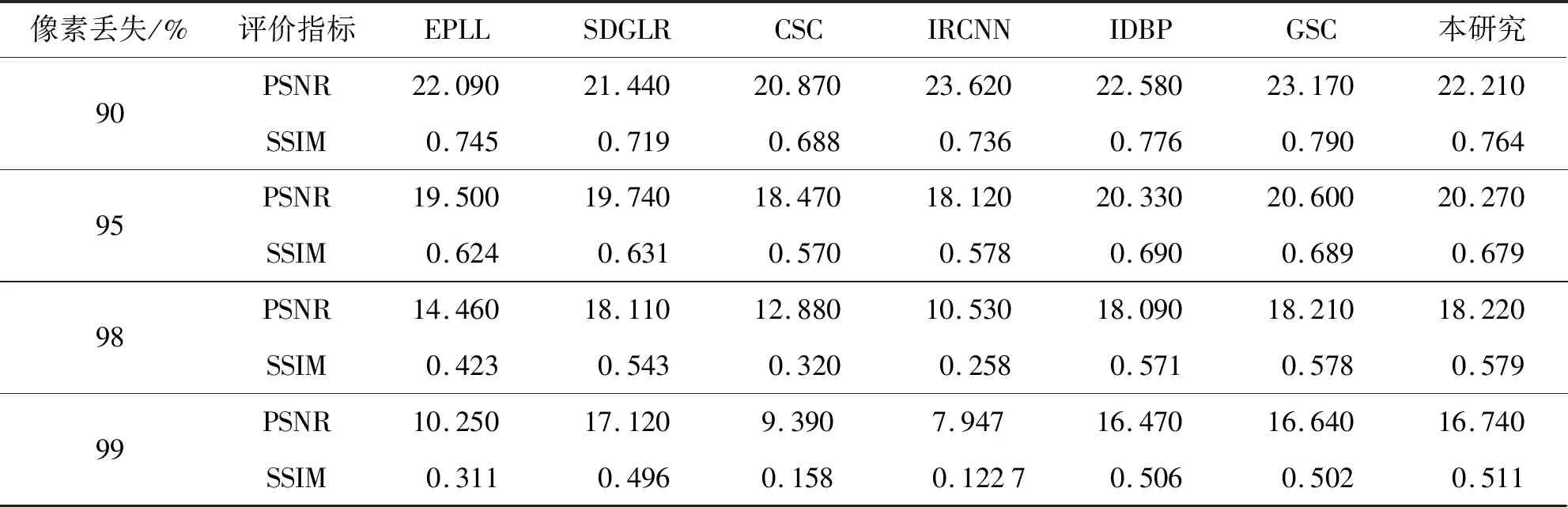
表1 不同方法在12张随机丢失90%以上像素的图像上实验结果比较Tab.1 Comparison by different methods on 12 test images with more than 90% randomly missing pixels

图4为针对Man图像随机丢失90%像素的几种算法结果比较.可以看到，本研究所提出的算法虽然PSNR不是最高，但是其视觉质量明显比主流的基于块学习的算法效果好.特别对于大量丢失像素的图像，基于深度学习和字典学习的方法，由于其性能强依赖于训练数据，使得其修复精度不高，局部图像纹理细节丢失，比如衣服袖子.基于非局部自相似算法，由于部分图像局部细节不存在明显的自相似性，因此容易造成过平滑或块效应，且会产生虚假的边缘结构信息，比如人脸面部.图5为针对Boat图像随机丢失90%像素的几种算法结果比较.同样的，本研究算法的视觉质量明显比主流的基于块学习的算法效果好，没有明显的块效应和过度平滑现象.表2列出了不同方法针对128 px×128 px图像的运行时间,其中笔记本电脑配置：Intel Core i5-8365U CPU 1.60 GHz，所有实验都运行在Matlab 2015b上.实验结果表明所提出的图像修复算法相比于现有图像修复算法速度提升6倍左右.

图4 Man图像的几种算法结果比较Fig.4 Comparison by different methods on the Man image

图5 Boat图像的几种算法结果比较.Fig.5 Comparison by different methods on the image

表2 几种算法在128 px×128 px图像上平均运行时间Tab.2 Average run time (in sec) on 128 px×128 px images (s)

5 结语

提出一种基于结构保持图拉普拉斯正则的图像修复算法.相比于传统的二阶图拉普拉斯正则化算法，引入梯度信息实现结构保持，使周围信息沿着图像梯度的法方向延伸至待修复区域，从而达到图像修复的目的.修复模型可以转化为线性方程组，并通过共轭梯度法实现快速求解，对于一张128 px×128 px的图像处理时间不到2 s.通过重建误差分析，对于分片平面图像，所提出的算法具有更小的误差下界.从结果上视觉比较，重建的图像没有明显的块效应，更加自然.