基于粒子群的三支聚类算法

高艳龙,万仁霞,,陈瑞典

(1.宁夏智能信息与大数据处理重点实验室，宁夏 银川 750021； 2.福建弘扬软件有限公司健康大数据研究院，福建 福州 350002)

0 引言

近几年,随着5G技术、物联网、云技术、区块链、人工智能产业的快速发展，这些技术时刻都在产生大量的数据，如何从复杂数据中提取有用的信息，这是数据挖掘的范畴.聚类是数据挖掘中的一个重要分支，其为一种无监督的学习方法.其中K-means算法是Macqueen[1]提出的一种基于划分聚类算法，能够从杂乱无章的数据中挖掘出有价值的信息，对这些信息进行聚类，同一类中的信息相似度高，不同类中的信息相似度低.

K-means算法对聚类中心的选择比较敏感，而且易陷入局部最优解[2-3].针对K-means算法的不足，有许多学者尝试用群体智能算法对K-means进行改进，粒子群优化算法作为群体智能算法典型，被广泛用于改进聚类算法[4-5].文献[6]首次将粒子群与K-means算法相结合，该算法的思路是用K-means方法得到的聚类中心，作为粒子群初始粒子.文献[7]提出了粒子群与模糊K-means结合的算法，该算法将k个初始数据作为初始粒子，调用粒子群优化算法寻优求得最优的聚类中心，最后再对得到的聚类中心数据进行模糊划分.文献[8]提出一种改进的粒子群和K-means混合聚类算法，该算法引入小概率随机变异操作,增加了粒子多样性，提高了算法全局搜索能力，粒子群的适应度函数采用方差来比较粒子好坏.

经典K-means算法是一种硬划分算法，也是一种典型的二支聚类算法，即对象只能属于某一类，这在相对离散的数据集中没有什么问题，但数据集中有不确定数据时，将数据强制划分，会带来很大决策风险.由此，文献[9]将类数据划分为核心域、边界域和琐碎域3部分，类由核心域和边界域两个域组成，提出了一种三支聚类算法.文献[10]用三支决策理论研究类与类的重叠部分，提出了一种处理重叠部分数据的三支决策聚类算法，把重叠部分数据划分到类的边界域.文献[11]提出了一种使用样本邻域将二支聚类转化为三支聚类的方法，该方法利用二支聚类的结果和每个类中元素的邻域收缩和扩张来刻画类组成.针对K-means算法易陷入局部最优解和聚类结果准确率低等问题，本研究引入粒子群优化算法和三支聚类，提出一种基于粒子群的三支聚类算法，来提高聚类算法的聚类质量.

1 相关概念

1.1 粒子群优化算法

粒子群优化算法(particle swarm optimization,PSO)[12]是两位学者从大自然中观察鸟类族群寻找食物信息传递中受到的启示而开发设计的群体智能算法.粒子群中的单一粒子对应于鸟类族群中的单一个体，算法赋予粒子拥有记忆，就像鸟类通过个体之间的合作与竞争来实现全局搜索食物，从而得到粒子个体最优值和全局最优值.

在PSO算法中，粒子群由n个粒子组成，由于粒子没有质量和体积，可以延伸到d维空间，Xi={Xi1,Xi2,…,Xid}，1≤i≤n.每个粒子通过调整自己的位置求得新解，通过比较并存储最优值，称为Pid；在d维空间里粒子种群寻找到最优值所对应全局最好的位置，称为Pgd.

粒子有速度v和位置X两个属性，v代表粒子移动的速率，X代表粒子移动的方位.速度v按下式更新：

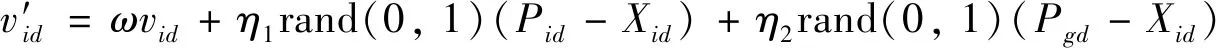
(1)

其中：vid表示第i个粒子在第d维度空间里移动的快慢；ω为惯性权重，一般取值在[0.1,0.9]之间[13]，其值越大，全局搜索能力较强，局部搜索能力较弱，其值越小，局部搜索能力较强，全局搜索能力较弱；η1、η2为学习因子，是调节Pid和Pgd相对重要性的参数，通常取值范围是[0,4][14]；rand(0,1)表示区间(0,1)随机数；Pid表示第i个变量个体极值的第d维；Pgd表示全局最优解的第d维.

粒子移动位置按下式更新：

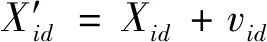
(2)

其中：Xid表示第i个粒子在第d维度空间里的位置.

粒子群优化算法有如下6个主要步骤.

步骤1粒子群初始化，设置粒子群规模，随机初始化粒子速度和位置.

步骤2计算所有粒子的适应度值.

步骤3对每个粒子的适应度值与其经历过最优位置适应度值对比，如果优于目前最好的，则更新粒子最优位置为Pid.

步骤4对所有粒子的适应度值比较，如果最好个体极值Pid优于全局极值Pgd，则全局极值Pgd更新为Pid.

步骤5用式(1)～(2)更新粒子速度v的和位置X.

步骤6若终止条件(最大迭代次数或足够好的位置等)达到，算法停止；否则,重复步骤2到步骤5.

1.2 三支聚类

三支决策[15-17]是把一个整体分为3个域来表示，即正域、负域、边界域.三支聚类[18-20]就是把三支决策引入到聚类算法中，重新定义对象和类的关系有3种，第一种是对象肯定属于某类(正域)；第二种是可能属于也可能不属于某类(边界域)；第三种是肯定不属于某类(负域).

给定一个数据集U={x1,x2,…,xn}，聚类结果为C={C1,C2,…,Ck}.三支决策聚类是由三个互不相交的集合表示一个类，即核心域、边界域、琐碎域，也称为CP、CB、CN.

CN=U-(CP∪CB)

(3)

其中：CP中的对象肯定属于这个类;CB中的对象可能属于这个类，CN中的对象肯定不属于这个类.

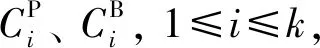
2 三支聚类算法的设计

粒子群优化算法可以整体上反映群体的簇群划分分布趋势，而三支聚类算法则可以有效地刻画类的边界点的分布细节.基于以上认识，设计一种聚类算法，以期吸收上述两算法的优点，达到更好的聚类质量.

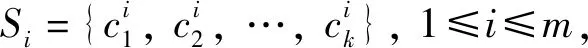
2.1 公式计算

1) 粒子的编码结构如下：

X11X12…X1dX21…X2d…X3d.…Xkd|v1v2…vk×d|f(x)

(4)

其中：Xkd表示粒子的位置;vk×d表示粒子的速度.

2) 当聚类中心确定后，根据最近邻距离把数据划分到最近的类：

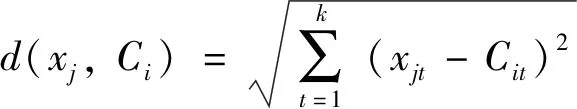
(5)

其中：xj表示第j个对象，1≤j≤n；Ci表示第i个聚类中心，1≤i≤k；xjt表示第j个对象的第t个属性；Cit表示第i个聚类中心的第t个属性.

3) 聚类中心的计算(均值)：

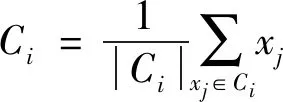
(6)

其中：xj为数据对象，1≤j≤n；|Ci|属于该类的样本个数.

4) 粒子群采用的适应度函数(误差平方和)：

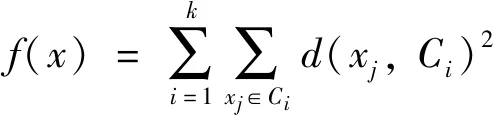
(7)

其中：d(xj,Ci)是样本xj到聚类中心Ci距离；函数f(x)是数据到相对应聚类中心的距离总和，要达到最小.

5) 为了平衡粒子的局部寻优能力和全局寻优能力，本研究中惯性权重ω采用线性递减策略：

(8)

其中：ω是惯性权重,ω∈(0.3,0.8);ωmax是惯性权重的最大值;ωmin是惯性权重的最小值;T是迭代总次数;i是迭代次数变量.

惯性权重采用线性递减有效地控制粒子的局部寻优能力和全局寻优能力强弱上的切换.

6) 选择合适的学习因子，能保证算法的收敛速度和搜索能力的均衡.本研究中学习因子采用下式更新：

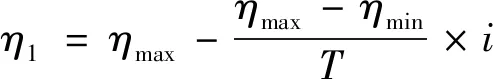
(9)

(10)

其中：η1、η2是学习因子，η1、η2∈[0.50,2.05]，ηmax是学习因子的最大值，ηmin是学习因子的最小值，T是迭代总次数，i是迭代次数变量.

学习因子采用单调递减、单调递增的方式，避免了粒子在局部最优范围徘徊和过早收敛到最优值，同时保证了算法的收敛速度和搜索能力的均衡.

7) 粒子群速度的上界和下界.粒子群中速度的上界和下界能维护粒子的探索能力平衡.速度选择过大，其探索能力强，但易于飞过最优解；速度选择过小，其探索能力变弱，易陷入局部最优.所以速度取值在速度的上界vmax和下界vmin之间.

8) 差值排序法[9].遍历类内所有数据到聚类中心的欧式距离，把距离按照从小到大的顺序排列disk(x1,Ci),disk(x2,Ci),…,disk(xn,Ci);然后依次计算disk(x2,Ci)-disk(x1,Ci),…,disk(xj,Ci)-disk(xj-1,Ci),…,disk(xn,Ci)-disk(xn-1,Ci)；最后找出第一个欧式距离最大的差值对，把x1,x2,…,xj-1对象放入Ci的核心域，xj,xj+1，…,xn对象放入Ci的边界域中.

2.2 算法步骤

输入：数据集U，聚类数目k，近邻数q，惯性因子ω，学习因子η1、η2.

步骤1初始化粒子群.在数据集中随机选取k个数据对象作为初始聚类中心，初始聚类中心值赋值给初始粒子，通过m次选取，形成m个粒子，初始化粒子的速度与位置.

步骤2用式(5)计算每个粒子中的所有数据对象到聚类中心的距离，根据最近邻距离原则对数据进行类划分.

步骤3用式(7)计算每个粒子适应度值.

步骤4对每个粒子的适应度值与其经历过最优位置适应度值对比，如果优于目前的位置，则更新粒子最优的位置为Pid.

步骤5对所有粒子的适应度值比较，如果最好个体极值Pid优于全局极值Pgd，则全局极值更新为Pid.

步骤6用式(1)～(2)分别更新粒子的速度和位置.

步骤7重复步骤2到步骤6，达到足够好的位置(或最大迭代次数)停止.

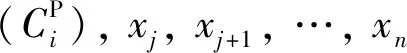
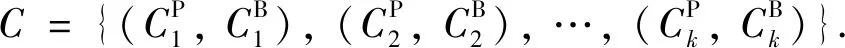
3 实验结果与分析

3.1 实验数据集

该实验环境为：Intel Core i7 2.8 GHz CPU；8 GB 内存；1 000 GB 硬盘；Windows 10 操作系统.采用 Matlab 语言编程实现.实验采用人工数据集和UCI数据集，如表1所示，其中D1、D2为人工数据集，其余7个数据集来自UCI数据库.人工数据集主要用以直观展示本研究算法PTWC(基于粒子群的三支聚类)和对比算法KM(K-means)、PSOC(粒子群聚类)的聚类效果，UCI数据集用以测试评价指标.

表1 实验数据集Tab.1 Experimental data set

3.2 聚类人工数据集

为了区别KM算法、PSOC算法与PTWC算法聚类结果，选取人工数据D1和D2做了实验，如图1～6所示(图中x、y为二维笛卡尔坐标系的坐标轴).

图1 数据集D1Fig.1 D1 data set

图1是未分类的D1数据集;图2是KM和PSOC算法在D1数据集上的聚类情况，可以看出两个算法具有相同聚类效果；图3是PTWC算法是在D1数据集上聚类情况，可以看出，算法不仅具有KM和PSOC的聚类效果，而且类的边界细节(“+”和“x”)也得到了刻画.边界细节的刻画为聚类的噪声分析提供了重要研究依据.

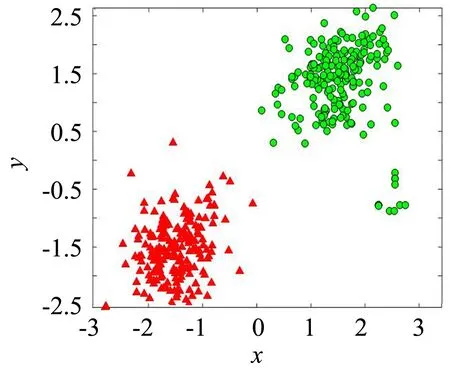
图2 KM和PSOC在D1上的聚类效果Fig.2 Clustering results of KM and PSOC on D1

图3 PTWC在D1上的聚类效果Fig.3 Clustering results of PTWC on D1

图4是未分类的D2数据集；图5是KM和PSOC算法在D2数据集上的聚类情况，可以看出两个算法仍然可以得到正确的聚类结果；图6是PTWC算法在D2数据集上的聚类结果，算法不仅具有KM和PSOC的聚类效果，而且每个类的边界细节也得到了刻画，处于上边区域的两个类存在交叠，即两个类的边界域(“+”和“◇”)存在重叠部分，类间对象的关系得到了更真实的展现.

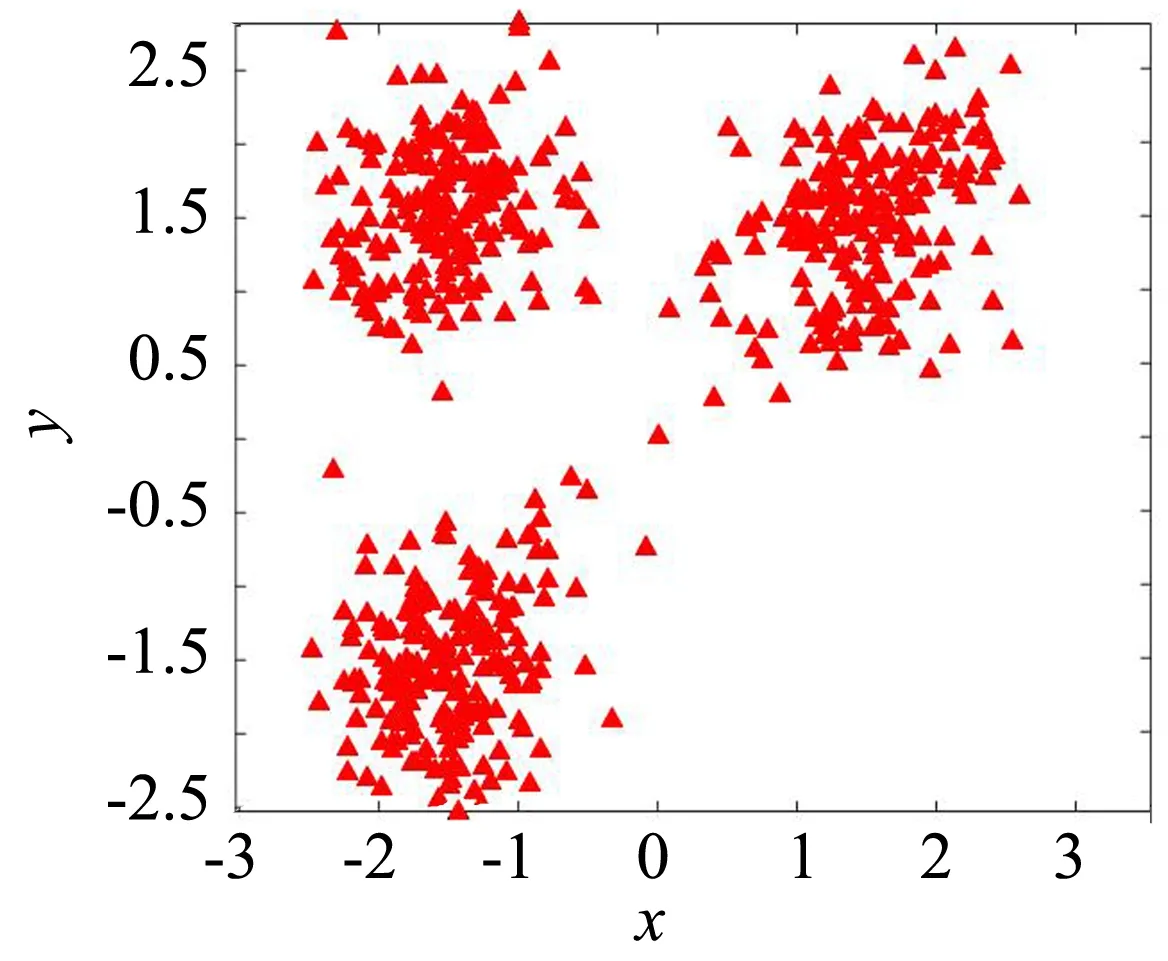
图4 数据集D2Fig.4 D2 data set

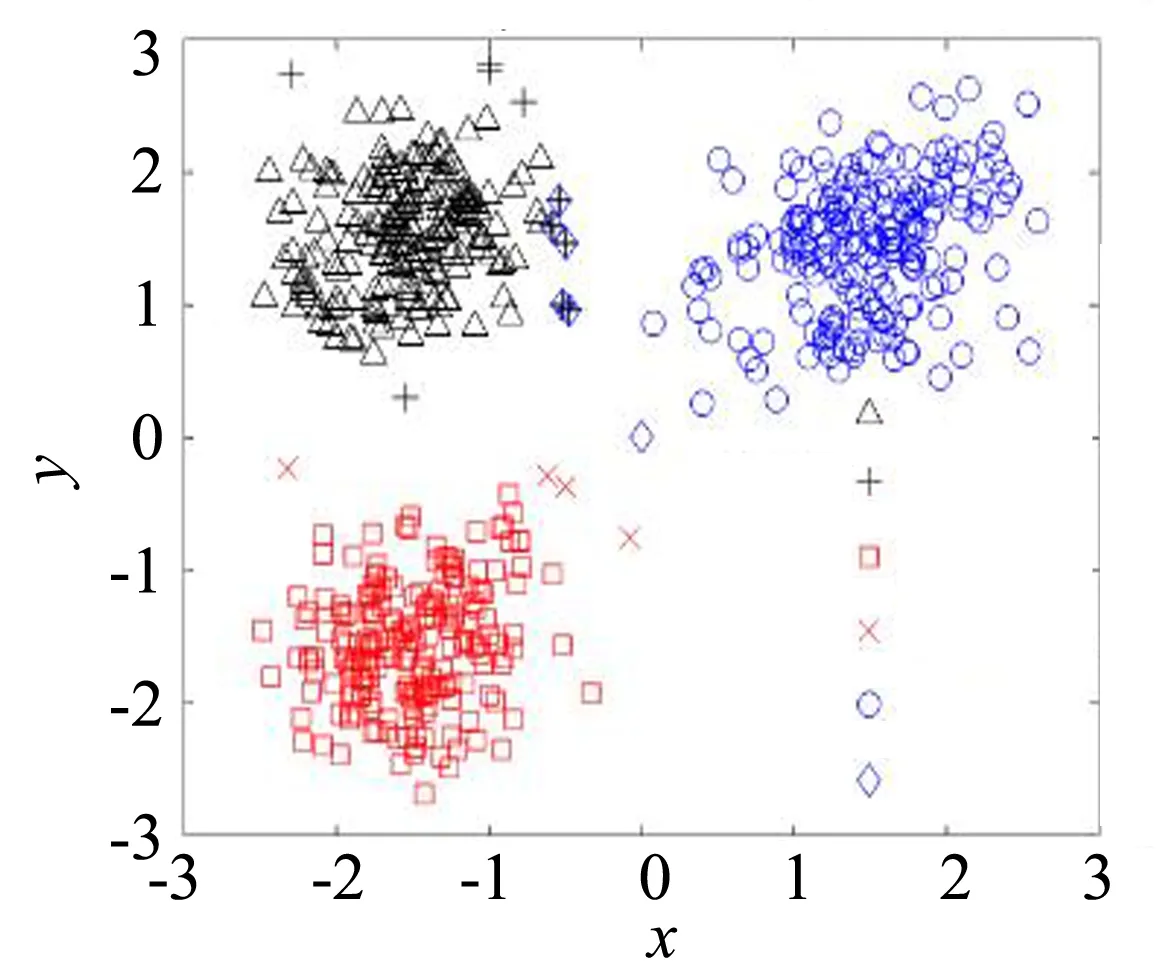
图6 PTWC在D2上的聚类效果Fig.6 Clustering results of PTWC on D2

3.3 聚类UCI数据集

3.3.1 聚类准确率与误差平方和

采用评价指标准确率ACC和误差平方和SSE来对比分析算法的优劣.

准确率(ACC)是一种类外部衡量指标，其值越高说明聚类效果越好.其计算式为：

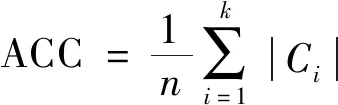
(11)

其中：|Ci|表示正确划分到类i的数据个数，n为数据的总数，k为聚类的数目.

在本研究PTWC、KM、PSOC 3种算法聚类的目标函数采用误差平方和函数(SSE).其计算式为：

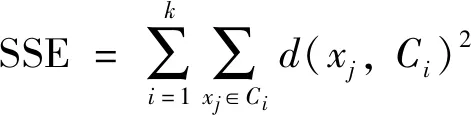
(12)

其中:d(xj,Ci)是类内数据对象到聚类中心点的距离;SSE的值是所有数据对象到其所在聚类中心的距离平方和，在相同的迭代次数下，SSE值越小，说明算法越好.

在UCI数据集Iris、Wine、German、Heart、Breast、Pima、Spambase中，分别用KM算法、PSOC算法和PTWC算法每次迭代100次，共运行100次取ACC的平均值和SSE的最小值做实验对比，实验结果如表2所示.

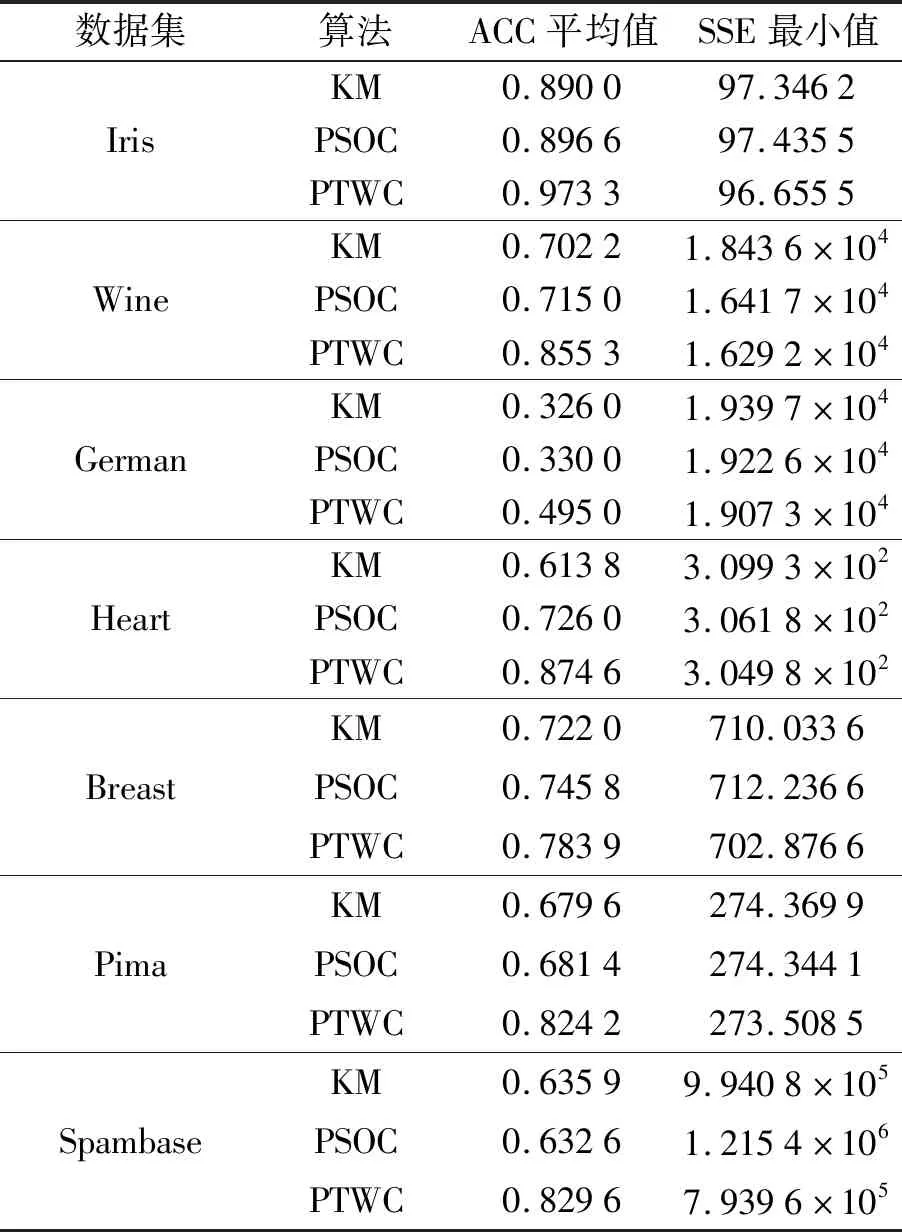
表2 UCI数据集上的实验结果Tab.2 Experimental results on UCI data set

从表2中可以看出，在7个数据集上，PTWC算法的ACC的值高于KM算法和PSOC算法的ACC值，PTWC算法的SSE值低于另外两个算法的SSE值，表明PTWC具有更好的聚类质量.这是因为通过粒子寻优，PTWC获得了最优的簇中心，确保了算法在划分数据集时的聚类结构质量，而通过边界域的最小邻居处理技术来进一步细化类间重叠部分和孤立点部分的归属，从而提高聚类的准确率.

3.3.2 寻优曲线变化

为进一步展示算法性能，记录了算法的寻优曲线过程.3种算法在UCI数据集上的最优值随迭代次数的变化趋势，如图7所示.

图7(a)～(g)分别记录了3种算法在数据集Wine、Breast、Heart、German、Iris、Pima、Spamdase的最优值在迭代100次的变化趋势.从7张图整体情况来看，在相同的条件下，KM收敛速度快，但易于陷入局部最优值；PSOC算法，在收敛时出现稍微震荡；PTWC算法全局寻优能力优于KM，且不易陷入局部最优解，收敛速度比PSOC算法快，而且PTWC比KM、PSOC更接近于最优值.这是因为KM依据最小距离原则划分数据，在一定数据规模下，能较快收敛，但易于陷入局部最小，而PSOC实际上是在KM的基础上再进行PSO寻优，双重迭代寻优导致计算时间开销增大，而PTWC借助PSO获得簇中心后，通过三支决策的方法来划分数据对象的归属，既确保了聚类的质量，又在时间开销方面避免了PSOC多重迭代的不足.

(a) Wine data set

4 结语

研究提出一种基于粒子群的三支聚类算法，算法通过粒子群全局寻优能力更新聚类中心，有效避免因收敛速度过快而陷入局部最优值，而在处理类与类的重叠数据和类内孤立数据时，采用了三支决策的方法，降低决策风险，从而提高了聚类结果的准确性.