基于支座反力影响线曲率差分的等截面连续梁损伤识别方法

唐盛华，张佳奇， 刘宇翔， 成 鹏

(湘潭大学 土木工程与力学学院 工程结构动力学与可靠性分析湖南省高等学校重点实验室，湘潭 411105)

1 引 言

桥梁服役期间，难免会因外部环境和荷载等的影响而引起结构的损伤。潜在的结构损伤甚至可能导致桥梁的坍塌，从而造成巨大财产损失和人员伤亡，因此有必要对桥梁的健康状态进行监测。目前对桥梁结构损伤的研究大致分为动力法、静力法以及模型修正等[1,2]。基于动力的损伤识别方法，一般采用频率、振型、柔度和模态曲率等因子来进行桥梁损伤识别研究[3-8]。Pandey等[9]利用损伤会引起结构刚度下降、柔度增加的特点，对损伤前后的模态柔度矩阵作差，用列向量最大值实现损伤定位； Liu等[10]根据有无损伤前信息提出了两种基于频响函数定位损伤的方法。基于动力损伤识别的方法对测量仪器精度要求较高，受外界环境的干扰较大，像温度和风等因素都会影响识别结果[11-13]。相较于前者，基于静力的损伤识别方法降低了对测量仪器的精度要求，受外界的影响也更小，因此亦具有重大的研究意义[14,15]。基于静力的损伤识别方法，一般是基于挠度、支座反力、转角和应变等因子来实现损伤识别[16-18]。王艺霖等[19]通过两跨连续梁的支座反力在受损后会有改变，然后根据损伤前后的支座反力信息作对比来判断损伤的大致位置；唐盛华等[20]用均布荷载作用下桥梁结构损伤前后的挠度曲率差进行损伤定位，依据挠度曲率差变化判断出具体的损伤程度。

上述基于静力的损伤识别方法大多要用到结构损伤前的信息，对于大部分缺少损伤前信息的在役旧桥显然无法适用。对此，李春良等[21]利用结构的对称性，实现了三跨变截面连续梁的损伤定位，并且能粗略地判断损伤大小；王艺霖[22]采用位移曲率差分的方法实现了判断简支梁结构的损伤位置。本文提出一种支座反力影响线曲率差分损伤识别方法，该方法不需要结构损伤前的信息，以三跨不等跨等截面连续梁推导了支座反力影响线曲率差分指标的损伤定位原理，而且基于该指标的规律给出了损伤程度定量方法。

2 损伤识别理论

以三跨不等跨连续梁的第一跨发生损伤为例，进行理论分析，如图1所示。其中P为从支座A移动到支座D的移动荷载，P到支座A的距离为z；图中的阴影部分为损伤区域，长度为ε，损伤单元的左端到支座A距离为a；损伤单元的刚度为kEI，其他位置的刚度为EI，桥梁三跨的长度分别为L1,L2和L3。以求中间支座B处的支座反力影响线为例，可由力法和图乘法求得。

图1 三跨不等跨连续梁

以简支梁为基本结构，当P荷载作用在梁上时，可根据力法建立基本方程，即

(1)

式中XB和XC分别为中间支座B和支座C的支座反力，δ11为单位力作用于支座B处时的点B位移，δ12为单位力作用于支座C处时的点B位移，δ21为单位力作用于支座B处时的点C位移，δ22为单位力作用于支座C处时的点C位移，Δ1P为移动荷载P作用下的点B位移,Δ2P为移动荷载P作用下的点C位移。

根据式(1)进行变化可得到支座反力影响线XB为

(2)

图2 单位荷载作用在支座B处的弯矩图

图3 单位荷载作用在支座C处的弯矩图

图4 弯矩图MP

(3)

(4)

(5)

(6)

(7)

(8)

由于Δ1P和Δ2P计算时会随损伤和移动荷载P位置的改变而不同，所以支座反力影响线分为两种不同的情况。

(1) 当损伤在跨内时

因为P作用在损伤左右两侧的计算公式相似，所以以P作用在损伤的左侧时(z≤a)为例，Δ1P和Δ2P为

(9)

(10)

(2) 当损伤在支座旁时

损伤在支座旁时即损伤的右侧和支座位置重合，此时a=L1-ε。与上相同，以P作用在损伤的左侧时(z≤a)为例，Δ1P和Δ2P为

(11)

(12)

根据损伤和移动荷载P的位置把相应式(6～12)代入式(2)，求得最终的XB值。

支座反力影响线理论上是一条由无数个点依次连接成的线，而在实际运用过程中，为减少移动荷载加载次数和支座反力影响线数据的数量，将梁等分成n-1个单元，n个节点，使移动荷载等间距加载在各节点上，并通过依次记录下各支座反力值，得到数据较少的支座反力影响线。具体的节点分布如图5所示。

图5 节点分布

图5梁下方的数字和字母代表节点编号，从左到右，从1依次递增到n。i和i+1表示损伤单元两侧的节点，f代表节点i左侧未损伤单元处的节点，j代表节点i+2右侧未损伤单元处的节点，n1和n2分别表示不同中间支座处的节点。

采用中心差分法求支座反力影响线各节点的曲率，公式如下,

(13)

2.1 损伤定位

为了简化本文的公式，令c1和c2代表公式中含有的常量，具体如下:

c1=P(δ22L2-δ12L3+δ22L3)

(14)

(15)

(1) 当损伤单元在跨内时，损伤定位指标D有以下规律。

在节点f时(损伤单元的左侧)，f取值范围为f∈[2,i-1]，

(16)

在节点i时，

(17)

在节点i+1时，

(18)

在节点i+2时，

(19)

在节点j时(损伤单元的右侧)，j取值范围为j∈[i+3,n1-1]，

(20)

从本文跨内单元损伤时损伤定位指标的规律可以看出，在未受损单元处节点的曲率差为一个定值，即在节点f和节点j处的D为定值，在受损位置(节点i，节点i+1和节点i+2位置)该值发生了变化。所以只要计算支座反力相应D值，画出图形，根据图形上发生了变化的点，即可判断发生损伤的单元位置。

(2) 当损伤单元在中间支座旁时，损伤定位指标D有以下规律。

在节点f时(损伤单元的左侧)，f取值范围为f∈[2,i-1]，具体值与式(16)相同。

在节点i时，

(21)

在节点i+1时(i+1=n1)，

(6c2kEI)

(22)

在节点i+2时,

δ22L1L2]+5kε(δ12L3-δ22L1)+ε[δ12L3-

δ22(L2+L3)]}/(6c2kEI)

(23)

在节点j时(损伤单元的右侧)，j取值范围为j∈[i+3,n2],

(24)

从本文支座旁单元损伤的五种情况可知，两跨未受损单元节点处(节点f和节点j)曲率差分值为两个定值。未发生损伤时，由于支座的影响，节点i+1和节点i+2处曲率差分值有所改变，而节点i位置处曲率差分值没改变(k=1时，式(16)与式(21)相同)；有损伤时，节点i、节点i+1和节点i+ 2处的值都发生了变化，因此可以根据此处曲率差分值变化的数目来判断是否发生损伤，也可以根据D值图是否有凸起凹下来判断。所以只要计算出支座反力相应D值，画出图形，根据图形上发生了变化的点，即可判断出损伤单元的位置。

将支座反力影响线曲率作差分，得到支座反力影响线曲率差分损伤定位指标D为

D=[D2D3…Dm…Dn - 1Dn]=

(25)

2.2 损伤程度定量

根据计算的D值结果，可以将损伤程度定量的计算方法按损伤单元位置分为三类情况，具体如下。

(1) 当损伤单元为边跨单元时

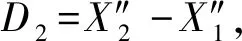
(26)

通过式(26)变形后，可得到损伤程度De，具体如下，

(27)

右侧边单元损伤时可将支座反力影响线值逆序后按左侧边单元损伤计算。

(2) 当损伤为跨中单元时

根据式(16,18)，变形化简后，可得到损伤程度De，具体如下,

(28)

式中Dj和Df两者相等，所以式(28)也可用Df替换Dj。

(3) 当损伤在中间支座旁单元时，以损伤单元在中间支座左侧为例。

根据式(16，22，24)组合化简后，可得到损伤程度De，具体如下，

(29)

当损伤单元在中间支座的右侧时，只需要将式(29)的Df和Dj互换位置。

3 算 例

3.1 三跨连续梁

三跨连续梁的跨径布置为50 cm+75 cm+50 cm， 5 cm划分一个单元，共35个单元，如图6所示。图6梁上方的数字为单元编号，下方的数字为节点编号，支座旁的数字代表支座编号。梁横截面尺寸b×h=6 cm×3 cm，材料的弹性模量为2.7×103MPa，密度为1200 kg/m3。

图6 三跨连续梁模型

由于实际桥梁结构中的损伤，如裂纹的产生、材料腐蚀或弹性模量的降低，一般只会引起结构刚度减小，而对结构的截面尺寸大小和质量影响较小。故在结构中，单元的损伤通过降低弹性模量来模拟。用有限元软件建立结构模型，移动荷载P=1 N，设定单元1、单元10和单元18发生损伤，具体的结构损伤工况列入表1，上述损伤单元位于梁的支座和跨中附近，而这些位置的剪力和弯矩值相较于其他部位更大，所以更容易发生损伤。

表1 三跨连续梁单元损伤工况

工况1的损伤定位指标D值图如图7所示。图7较为明显的一处突变在节点10、节点11和节点12，意味着这附近存在损伤，而节点10、节点11和节点12分别对应理论上的节点i、节点i+ 1和节点i+2，所以可以判断出单元10损伤，这与设定损伤单元相符。在节点2和节点3也存在不太明显的突变，且4#的D值相较于其他支座，在该处的突变不明显。这一方面是因为该处的损伤较小，同时整体D值的数值波动较大，从而掩盖了该位置的损伤；另一方面是支座离损伤位置越远，损伤引起支座反力变化也会越小，因此出现了4#的D值对该处损伤不敏感。在实际的桥梁测量过程中，可以采用隔跨布置支座反力测点来避免支座离损伤较远对损伤不敏感的情况；通过画局部的D值图来突出损伤以及规避其他D值的影响。图8为2#的局部D值图，可以明显观察到节点2和节点3为突变点。正常的损伤都会引起三个节点的D值发生突变，但对于边单元损伤，如1号单元损伤，由于1号单元无左侧点D值，所以只有节点2和3两个突变点。因此可以判断单元1也存在损伤。工况1在节点26左右发生了突变是因为支座的影响，但从突变点个数只有两个可判断该支座处没有损伤。同理，工况2从图9可判断出单元1、单元10和单元18处有损伤。同样作出2#在单元1处的局部D值图，如图10所示，可以看出单元1存在损伤。

两种工况都采用2#的D值，并根据损伤单元位置对其损伤程度进行计算，具体结果列入表2。工况1取两个不同支座的D进行计算，从结果可以看出，用距离损伤部位较远支座的D计算会对结果产生较大的误差。所以在选用支座计算损伤程度时，选用的支座不宜离损伤位置太远。

损伤定位指标判断的损伤情况和设定工况相同，说明损伤定位指标在损伤定位上具有可行性。从本文两种多损伤工况的D值判断结果可知，该指标对等截面连续梁多单元损伤的损伤程度能够准确识别。

图7 三跨连续梁工况1的D值图

图8 2#局部D值图

图9 三跨连续梁工况2的D值图

图10 2#局部D值图

表2 三跨连续梁损伤单元的损伤程度计算结果

3.2 四跨连续梁

在三跨连续梁算例的基础上，对某四跨等截面连续梁工程实例进行分析，探究该方法对实际工程是否具有实用性。某四跨混凝土连续梁的跨径布置为20 m+30 m+30 m+20 m， 2 m划分一个单元，共50个单元，有限元模型如图11所示，图11梁上圆圈的数字为单元编号，梁下数字为节点编号，支座旁的数字为支座编号。四跨连续梁采用小箱梁截面，尺寸如图12所示，采用C50混凝土。

移动荷载P=1 kN，设定桥梁的单元10、单元18和单元33同时发生损伤，具体的损伤工况列入表3，损伤单元的设定和三跨连续梁算例的原因相同。

图11 四跨等截面连续梁

图12 横截面尺寸(单位：cm)

表3 四跨连续梁单元损伤工况

四跨连续梁的算例选取了2#和4#隔跨支座的D值图，从图13可以判断出单元10、单元18和单元33发生了损伤；从图14也可以判断出单元10、单元18和单元33发生了损伤。从图14的4#值来看，单元10的损伤不是很明显，但2#值却可以较为清楚地识别，这也说明通过选取隔跨支座D值的方法能避免因支座远离损伤位置而对损伤不敏感的问题。两种工况都采用2#的D值，并根据损伤单元位置对其损伤程度进行计算，具体结果列入表4。

图13 四跨连续梁工况1的D值图

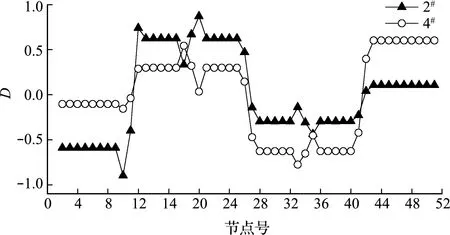
图14 四跨连续梁工况2的D值图

表4 四跨连续梁损伤单元的损伤程度计算结果

两种工况的损伤判断都和实际设定损伤单元相同，说明该方法对工程实例损伤位置的识别也有良好的效果。根据推导的公式对损伤单元进行损伤程度计算，计算得到的结果与设定的损伤程度基本相同，说明该损伤程度计算方法对四跨等截面连续梁工程实例也具有实用性。

4 结 论

(1) 基于支座反力影响线曲率差分的等截面连续梁损伤识别方法，不需要桥梁损伤前的信息；以三跨不等跨等截面连续梁做理论推导，发现支座反力影响线曲率差分值在损伤位置发生突变，根据支座反力影响线曲率差分曲线的突变，可以判别出结构的损伤位置。根据理论损伤位置的曲率差分值的变化规律，推导出了各位置损伤程度的计算方法。

(2) 用三跨连续梁以及四跨连续梁工程实例证明了支座反力影响线曲率差分的损伤定位具有可行性，针对曲线图中突变不明显的问题，采用局部详图的解决方法；对不同部位设定的理论损伤值和识别得到的损伤程度进行比较，两者的数值相近，说明该损伤程度定量方法具有可靠性。

(3) 在实际的桥梁中，一般采用千斤顶来测量支座反力，但在精度方面还存在不足，测量步骤也较为麻烦，因此有必要开发一种精度更高和测量更方便的支座反力测量系统。另外，支座反力影响线曲率差分的方法目前仅针对各单元独立损伤的情况，对于相邻多单元同时损伤和一个单元内部局部损伤情况还有待进一步研究。