幼鱼体长差异性对群游推进效率的影响研究

龙泽宇， 胡 晓，张永年， 张 奔， 杨国党， 石小涛

(三峡大学 水利与环境学院，宜昌 443000)

1 引 言

鱼类作为地球最古老的生物之一，经过亿万年的自然选择，逐步形成了超强的游动能力[1,2]。为了适应复杂的海洋环境，绝大多数鱼类都进化出了流线型的外形和柔软的身躯，不仅可以减少洋流产生的阻力，还可大大增强其游动的机动性。仿生学者们发现，超过88%的鱼类采用尾鳍摆动的推进方式，能够保证其在最小能耗下达到最理想的游动速度。另外，鱼类还能感知流场中涡流的存在，通过控制自身的游动方式来利用涡流产生的能量，从而节省能耗提高游动效率。因此，研究鱼类的游动机制，探寻其与流场间的作用机理，对研制新概念的水下仿生机器人具有重要的指导意义[3,4]。

随着数学理论建模的成熟，学者对水下鱼类的流场变化、游动机制以及推进效率进行了深入研究[5,6],发现大部分鱼类是通过与水体间的相互作用推动自身向前移动，从而根据流场变化估测鱼体产生的推力及其水动力效率[7,8]。通过数值模拟和实验的方法来研究鱼体，其中通过鱼体每次摆动产生的前缘涡周期性的变化(最终演变形成逆卡门涡街)来分析其游泳机制。Li等[9]通过数值模拟对斑马鱼进行了量化分析，准确地预测了鱼体的运动以及流场涡结构的特征，并利用二维粒子图像测速和运动学数据相结合对斑马鱼的推进效率进行研究；Akanyeti等[10]结合生物力学、流体力学和仿生学证明了稳定游泳和向前加速之间存在根本的区别，而且加速鱼类可以通过改变涡旋环的几何形状来提高推进效率；章永华[4]围绕仿生波动鳍的结构设计、数值计算和实验验证三方面综合分析了游动性能的影响，并给出了鱼鳍波动游动时流场信息以及总体受力情况,也从涡动力学角度揭示了鱼体的流体力学机理。

鱼类游动的模式各式各样，不同模式对应着不同的游动需求，常兴华[11]建立了一套适用于鱼类数值模拟的方法，通过分析单个鱼体摆动以及鱼群的群游对其推进机理进行初步探讨；Killen等[12]研究发现鱼类很少单独游动，成群游动状态下经常通过调节尾流结构来实现鱼群的相互交流；文献[13，14]采用数值模拟的浸入边界法，对鱼类游动的推进机理进行仿真研究，并分析了鱼群菱形结构的水力学特性，发现菱形结构有助于减少阻力和提高推进效率，降低了动力消耗；Herskin等[15]研究发现鱼群中不同位置的鱼体其行为变化各不相同(如尾巴拍击的频率)，发现鱼群领头鱼比跟随鱼的摆尾频率高，摆尾幅度低，能量消耗大；李超[16]首次通过卡门游动对群鱼进行数值模拟，分析了鱼群编队阵型对游动效率的影响，提出了卡门游动效率计算公式，评价了鱼体对涡流的利用率。综上所述，国内外相关学者只研究了群鱼的空间排列，并未考虑体长变化对群游效应、能耗以及推进效率的影响，因此本文基于前人的研究基础对群鱼做了进一步详细研究。

由于实验过程中真鱼的游泳形态并不是稳定不变的，且实验过程无法规律性地观察到群鱼的推进，本研究模拟结合实际条件对群鱼的游泳效率进行分析。本文首先参考文献[17]，确定分布位置为三角形的鱼群，采用数值模拟分析群鱼以及鱼体间的力学特性，结合推力系数以及功率系数等参数，揭示了群鱼运动过程中的推进效率，相关模拟结果为鱼群群游推进过程与高效游泳机制的形成提供了理论支撑。

2 材料与方法

2.1 物理模型

为了提高模拟结果的真实性，模拟的部分基本数据来自于三峡大学水利与环境学院生态实验室中草幼群鱼的动水实验。如图1所示，模拟基于草幼鱼的厚度采用具有移动波浪运动的NACA0012翼型，鱼群的排列方式和间隔距离是根据真实鱼体分布间隔和参考文献[17]的对比结合，设鱼体体长为L，将上游鱼和下游鱼的纵向间距(平均值)设置为S=0.5L，下游两条跟随鱼之间的横向距离设置为T=0.3L。

图1 鱼群的排列方式

当草鱼幼鱼开始前进时，整个身体弯曲成C形，随后开始向前加速，尾部在5～6个尾拍后游泳速度开始稳定，当7～8次尾拍后，草幼鱼身体躯干逐渐笔直(逐渐开始滑行)。所以本模拟选取(数字化图像)1～7次之间的摆尾图像，提取鱼体的中线坐标，然后将中线的点坐标进行拟合，其拟合的波动方程为[18,19]

y(x/L,t)=a(x/L)sin[2π/λ(x-StUt)]

(1)

式中L为草鱼幼鱼的体长，t为时间，λ为鱼体的波长(λ的波动区间为0.8L～1L)，f为频率，U为鱼体的前进速度。

鱼体横向体波动的振幅包络线方程a(x/L)为[20]

a(x/L)=0.02-0.08(x/L)+0.16(x/L)2

(2)

2.2 网格划分

本次模拟采用有限体积法对其进行离散化，将整个实验过程群鱼的斯特劳哈尔数St设为0.3，雷诺数Re设定为1.2×104。为了探索实际鱼群游泳机制，防止运算过程中出现负体积，保证计算结果的收敛性，实验过程中生成的网格数约为 2.63×104，大约1.34×104的结构化和非结构化的混合网格节点，从图2可以看出，整个求解域分两部分组成(为了减少计算步骤)，第一部分是鱼体摆尾影响内的变形区域，第二部分是非加密区域的不变形区域[21,22]。

图2 网格划分模型

2.3 计算方法

整个鱼体的推力系数CT表达式为

(3)

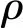
鱼体波动所需的功率Ps计算公式为

Ps=∮(pn)vsdA

(4)

式中p为鱼表面压力，n为鱼表面元法向因子，vs为鱼表面元横向速度，dA为表面元的微分。

功率系数CP为

(5)

(6)

2.4 研究方法

为研究鱼群体长变化对鱼群游动的影响，本文通过数值模拟的方法分析了不同体长条件下群鱼的游泳效果。由于群体间体长的差异，此次模拟将鱼群分为3个组合等差排列的鱼体，分别为组合1，上游鱼与下游鱼体长差异性较小，ΔL=0 cm，0.5 cm 和1.0 cm，上游鱼的体长都为L=10 cm，下游鱼体长小于上游鱼；组合2，体长差异性ΔL=2 cm，4 cm和6 cm；组合3，上游鱼的体长小于下游鱼，下游鱼体长为L=10 cm，其中体长差异性ΔL=-2 cm，-4 cm和-6 cm，如图3所示。

通过鱼群个体及群体间的涡量、推力、功率及推进效率的变化关系，分析了鱼群的群游效果，揭示了鱼群在群游状态下的理想体长分布。

图3 不同体长差值组合

3 结果与分析

3.1 单尾鱼的水动力学分析

如图4所示，为模拟单尾鱼的一个周期周身涡量变化云图，其中涡量矢量，红色表示流体逆时针旋转，方向指向平面外，蓝色表示流体顺时针旋转，方向指向平面内。

结果表明，试验幼鱼在一个周期内都有一正负尾涡脱落，涡量值相近。在t=0～1/4T和t=(3/4～1)T之间，正旋涡不断扩大，有明显的流体加速逆时针旋转。当t=1/4T时，逐渐从尾缘脱离，涡脱落的方向与鱼尾近似垂直，鱼体向左摆尾达到最大限度，此时紧靠鱼尾部的速度矢量表现为顺时针旋转。t=3/4T时，鱼的躯体处于最大弯曲阶段，鱼体振幅达到最大值，此时在鱼体尾部逐渐产生一个红色逆时针的旋涡。t=(1/4～3/4)T时，是鱼体向右回摆阶段，鱼体后方横向和轴向流体加速，涡不断扩大，直到涡脱落。除了在鱼体尾部有涡的形成脱落，鱼体周身由弱涡结构包围，未见明显的体涡脱落。

图4 单尾鱼的周身涡量变化云图

为了进一步说明模拟研究的涡量推进，对单尾鱼自推进推力进行计算分析，选取测量时间不同的两个摆尾周期，如图5所示，阴影部分为推力系数负值区域，推力系数为正值时，单尾鱼游动加速，且在t=1/4T和3/4T尾涡脱落时，推力系数达到峰值；推力系数为负值时，推力系数出现波谷，单尾鱼游动减速。

图5 单尾鱼的推力系数及游动速度

3.2 群鱼的尾流结构对比与分析

首先通过单尾鱼的水动力学变化，对群鱼进行对比分析。采用Weigand的研究理论[24](涡环的动能与涡环直径的大小成正比，与射流角度成反比，涡环d/D越接近1时，涡环具有的动能越大，推动效率越高)，对鱼群不同状态下的射流角度θ、涡环内径D以及涡核的直径d进行了测量，由于实验的缺陷不能对鱼群进行定量分析，因此本文通过数值模拟的方法分析了单尾鱼及群鱼间尾流流场的变化，并通过依次递增鱼体间的体长差值，对其尾流结构进行了分析。

鱼群在一个摆尾周期内尾涡会出现规律性变化，整体的尾涡结构先逐渐增大后减小，鱼体运动达到最大摆尾幅度时，开始有新的尾涡形成。上游鱼和下游鱼在一个摆尾周期内都生成二个旋涡，当鱼体尾部回摆到中垂面时，鱼体周身的尾流涡开始脱落，且鱼体游动尾流逐渐产生新的尾旋涡。随着旋涡的变化可以看出，上游鱼群游动时产生的尾涡结构和演化规律与下游鱼并不相同，其中上游鱼尾流中的涡结构相对比较稳定，而下游鱼尾部区域却不会形成稳定尺度的涡结构(上游鱼头部和下游鱼两侧的负压逐渐增强，尾流产生的正压相对增加)，如图6所示。

图6 鱼群的周身压力和涡量云图

本文首先分析了无体长差异性ΔL=0 cm的鱼群(鱼体体长为L=6 cm，7 cm，8 cm，9 cm和 10 cm)，如图7(a)所示，群鱼的尾流结构平均分布在0.423～0.493范围内，且群鱼的尾流结构(d/D)随幼鱼体长的增大而减小。

图7 鱼群ΔL =0 cm尾涡结构和各成员推力系数

通过实验数据对比，发现幼鱼群鱼的尾流结构d/D值降低时，群鱼的作用推力也在逐渐减低，如当幼鱼鱼群尾流涡结构d/D值下降时，推力下降到一定范围会达到波谷。如图7(b)所示，是组合一中无体长差ΔL=0 cm的三条鱼的推力系数变化曲线，上游鱼的推力系数与上节单尾鱼的推力系数对比，没有明显变化；但下游的两条鱼并排游动，水流受另一条鱼阻挡而且产生负压区，两条鱼之间的推力系数有很明显的差别。

对不同体长差异的各组合鱼群进行分析，如 图8 所示，上游鱼的尾流涡结构d/D平均为 0.423，通过对尾流涡结构的函数积分，得出组合一中ΔL=0 cm 的鱼群(鱼体体长为L=10 cm)尾流涡结构d/D平均为0.493，为上游鱼的1.2倍；ΔL= 0.5 cm 的鱼群尾流涡结构d/D平均为0.489，ΔL=1 cm的鱼群尾流涡结构d/D平均为0.493；组合二中ΔL=2 cm的鱼群尾流涡结构d/D平均为0.506，ΔL=4 cm的鱼群尾流涡结构d/D平均为0.520，ΔL=6 cm的鱼群尾流涡结构d/D平均为0.524；组合三中ΔL=-2 cm的鱼群尾流涡结构d/D平均为0.456，ΔL=-4 cm的鱼群尾流涡结构d/D平均为0.415，ΔL=-6 cm的鱼群尾流涡结构d/D平均为0.344。

图8 尾流涡结构数值

综上所述，上游鱼体长大于下游鱼体长ΔL>0 cm时，整体鱼群尾流结构(d/D)随体长差异的增大而增大；上游鱼体长小于下游鱼体长ΔL< 0 cm 时，整体鱼群尾流结构(d/D)随体长差异的增大而减小，且ΔL<0 cm时的尾流结构(d/D)均小于ΔL>0 cm时的尾流结构。

3.3 群鱼的游泳水动力学分析

分析群鱼的推力系数，如图9所示，结合推力系数发现组合一中无体长差异性ΔL=0 cm的鱼群整体产生的推力系数通过函数积分计算得平均为4.66×10-3，ΔL=0.5 cm的推力系数平均为5.11×10-3；ΔL=1 cm的推力系数平均为 3.89×10-3；组合二中ΔL=2 cm的鱼群整体产生的推力系数平均为1.71×10-3；ΔL=4 cm的推力系数为-8.0×10-4；ΔL=6 cm的推力系数为 -5.1×10-4；组合三中ΔL=-2 cm的鱼群整体产生的推力系数平均为2.75×10-3；ΔL=-4 cm的推力系数为9.51×10-4；ΔL=-6 cm的推力系数为 1.07×10-3。

图9 鱼群整体的推力系数

对比不同体长组合的群鱼，发现上游鱼的推力系数随下游鱼的大小不会有明显改变，但整体会随体长的变化发生明显的差异，上游鱼体长大于下游鱼体长ΔL>0 cm或上游鱼体长小于下游鱼体长ΔL<0 cm时，鱼群整体推力系数随体长差异的增大而减小，且组合一中ΔL=0.5 cm排列下的鱼群整体产生的推力系数要远高于其他组合鱼群。

3.3 群游的推进效率分析

通过对上游鱼和下游鱼的功率消耗进行比较，发现下游鱼的平均功率消耗较小(模拟中发现下游鱼的游泳行为可能会受到上游鱼的影响，整个游泳过程中下游鱼可能会降低其波动幅度或频率，来调整其推力，与其形成相对固定的距离，以便高效地利用上游鱼产生的尾涡效果，近似于鱼体的圆柱绕流效应)。首先通过群鱼中各成员的推力系数，对模拟结果进行了对比分析，发现下游鱼体之间的推力系数随着上游鱼尾部推力系数的变化而变化，从图7(b)可以看出,上游鱼和下游鱼之间的推力差异(其中上游鱼的推力系数小于下游鱼的推力系数，近似于单尾鱼的推力系数，且相较于单尾鱼群鱼的平均推力系数至少增加)。另外发现，随着鱼群之间体长差值的增加，整体的推力系数也在发生改变，当鱼群之间存在差异性时，随着鱼群间体长差值的逐渐增加，鱼群的平均推力系数在降低(近似于正态分布)，如图9所示。

图10 功率系数变化

如图10所示，当整体摆尾频率、摆尾幅度和游泳速度不变时，随着鱼群中体长差值的增大，下游鱼的功率系数逐渐降低，所以推进效率也在逐渐降低。本文分析了不同体长组合鱼群的功率系数，组合一中无体长差异性ΔL=0 cm的鱼群整体的功率系数平均为1.70×10-2，ΔL=0.5 cm的功率系数平均为1.49×10-2，ΔL=1.0 cm的功率系数平均为1.31×10-2；组合二中ΔL=2 cm的鱼群整体的功率系数平均为1.03×10-2，ΔL=4 cm的功率系数为7.10×10-3，ΔL=6 cm的功率系数为5.79×10-3；组合三中ΔL=-2 cm的鱼群整体的功率系数平均为1.58×10-2，ΔL=-4 cm的功率系数为1.51×10-2，ΔL=-6 cm的功率系数为1.57×10-2。对比发现鱼群上游鱼与下游鱼无差异性，体长差值为ΔL=0 cm时，整体的功率系数最高。

如图11所示，最后结合推力系数与功率系数，得出推进效率进行分析，发现群鱼产生的推进效率最高的组合一中ΔL=0.5 cm为17.2%，最低的组合二ΔL=4 cm平均为负值效率。综上所述，与单尾鱼相比，整体的功率消耗降低，组合一无差异性ΔL=0.5 cm的群鱼推进效果最佳。

图11 推进效率变化

4 结 论

本文分析了单尾幼鱼游动过程中的周身流速及涡量。之后采用数值模拟的方法对比分析了多组鱼群(上游一条鱼，下游两条鱼)体长不同的自推进状态下的游动，通过推力以及能耗等方面的参数对其进行了分析，间接揭示了群鱼运动过程中的推进效率，为水下仿生鱼组合提供了新思路。

(1) 对群鱼的尾流涡结构进行了分析，不同组合鱼群中上游鱼的体长不同，其脱落的尾涡对下游鱼游动推进影响不同。

通过对比不同体长差异性的群鱼，发现ΔL=6 cm时产生的尾流涡结构相对较高，上游鱼体长大于下游鱼体长(ΔL>0 cm)时，整体鱼群尾流结构(d/D)随体长差异的增大而增大；上游鱼体长小于下游鱼体长(ΔL<0 cm)时，整体鱼群尾流结构(d/D)随体长差异的增大而减小。

(2) 随着鱼群自身体长的变化以及布局的改变，鱼群的平均推力也相对增加，不同组合推力系数依次为0.5 cm>0 cm>1 cm>-2 cm>2 cm>-6 cm>-4 cm>6 cm>4 cm，功率系数为0 cm>-2 cm>-6 cm>-4 cm>0.5 cm>1 cm>2 cm>4 cm>6 cm，对其推进效率进行对比发现，ΔL=4 cm时整体的推进效率最低，ΔL=0.5 cm时整体的推进效率最高，为最佳的鱼群组合。