三阶模态耦合效应下悬索的1∶1主共振与稳定性分析

闵光云，刘小会，蔡萌琦，易航宇，孙测世2,

(1.中山大学 中法核技术与工程学院，珠海 519082；2.重庆交通大学 省部共建山区桥梁及隧道工程国家重点实验室，重庆 400074；3.重庆交通大学 土木工程学院，重庆 400074； 4.成都大学 建筑与土木工程学院，成都 610106)

1 引 言

悬索结构具有质量轻、阻尼小和柔度大的特点，因而广泛运用于土木工程中，如拱桥[1,2]、斜拉桥[3,4]和架空输电线[5，6]等。在风雨激励、地震作用和车辆冲击荷载等的作用下，悬索结构易发生振动，其振动行为非常复杂，因此分析悬索结构的振动特征已成为学术界的热点研究。

悬索的计算理论最早形成于16世纪末，成熟于20世纪中期,19世纪初，Poisson建立了悬索的运动方程[7]。Routh[8]在Poisson的研究基础上求解了松弛悬索的固有频率。20世纪中期，Pugsley[9]对比了张紧悬索和松弛悬索的振动特性，发现垂度是影响两者振动特性最为关键的因素。当悬索发生振动时，其模态之间会发生复杂的耦合效应。Benedettini等[10]研究了悬索面内和面外模态之间的非线性耦合现象，提出了一个简单而有意义的二自由度模型，并用三阶摄动分析法求解了该模型的动力学平衡方程，给出了模态耦合效应的证据。Rao等[11]在文献[10]的基础上研究了悬索结构面内和面外模态之间的 2∶1 内共振，发现当平面内的振动频率约为平面外的振动频率两倍时，振动方程的二次非线性项对悬索的性能有显著影响。20世纪末期，lee等[12]采用三自由度模型研究了平面激励作用下悬索面内模态和面外模态间的共振效应，用二阶非线性摄动法得知面内模态和面外模态之间存在 1∶1 和 2∶1 两种共振模式。21世纪初期，Zhao等[13]进一步研究了悬索在主共振作用下的模态间的 3∶1 内共振，利用Newton-Raphson法得到了悬索结构的幅-频响应曲线，并对解的稳定性进行了分析。

为了简化振动模型和便于推导振动方程，大部分科研学者们都忽略了悬索的弯曲刚度，而理论上悬索的弯曲刚度会随着其自身直径的增加而增加。基于此，赵跃宇等[14]研究了弯曲刚度对悬索非线性固有频率的影响，发现弯曲刚度对高阶频率和面外频率的影响更为显著。吴庆雄等[15]推导了考虑弯曲刚度影响的悬索自由振动解析解，修正了传统的Irvine参数。弯曲刚度会影响悬索的固有频率，进而使得其发生共振的条件产生偏移。吕建根等[16]在文献[14]的基础上研究了弯曲刚度对悬索面内和面外模态之间的 1∶1 内共振的影响。另外学者们还考虑了白噪声[17,18]和风雨激励[19，20]下悬索复杂的动力学特性，促进了悬索非线性动力学研究的发展。

由于非线性理论的蓬勃发展，学者们逐渐由研究单个悬索构件的振动转向索-梁耦合振动[21,22]和索-拱[1，2]耦合振动等。赵跃宇等[2]建立了索-拱耦合结构的动力学模型，并运用多尺度法分析了该模型中拉索可能发生的共振模式，确定了拉索参数共振和亚谐波共振的发生条件，并探讨了影响拉索共振的因素。彭剑等[19]采用时滞减振技术对索-梁组合结构进行了振动控制分析，发现通过调节控制增益和时滞值，可增大阻尼比，避免共振域，从而对索-梁组合结构实现减振。

本文在以上学者们的研究基础上，基于哈密顿准则推导了悬索的振动方程，考虑了悬索的前3阶模态之间的耦合效应，利用Galerkin离散方法将无穷维系统转化为三维耦合振动系统，采用多尺度法分析了悬索的一阶、二阶和三阶 1∶1 主共振，得到了一些具有现实意义的结论，能给予实际工程一定的参考。

2 振动微分方程

首先建立图1所示的悬索数学模型，悬索无高差且两端铰接，以左铰接点为坐标原点建立笛卡尔坐标系，x轴正方向沿两铰接点的连线向右，y轴正方向竖直向下。

图1 悬索数学模型

图1中u1为悬索轴向的动态位移，u2为悬索竖向的动态位移。

根据哈密顿变分准则可得

(1)

式中δkv为悬索的动能，δΠ为悬索的势能，δw′为非保守力做功。

悬索发生振动时，轴向的振动很微弱，主要以竖向的振动为主。根据式(1)可得到悬索竖向的振动方程

(2)

式中m为悬索的单位质量，y为悬索的静态构型曲线，t为时间变量，l为跨径，EA为拉伸刚度，EI为抗弯刚度，H为初始张力，μ为阻尼系数。

经实验观测到的悬索的一阶和二阶模态的振幅较大，三阶模态振幅较小，而第四阶模态的振幅几乎观测不到[23]，因此本文只考虑前3阶模态。

将悬索的竖向位移写为

(3)

(4)

考虑外部激励的作用效应，接着将式(3)代入式(2)，并根据Galerkin法可得到考虑悬索的前3阶模态耦合的振动常微分方程组为

(5a)

(5b)

(5c)

式(5)涉及的系数详见附录，本文不再赘述。

3 摄动分析

近年来，学者们采用不同的非线性定量分析方法来解决不同的非线性振动问题，其中多尺度法[21-28]应用最广泛。为满足多尺度法的求解形式，引入小参数ε，并将式(5)改写为

2Vεcos(Ωt)

(6a)

(6b)

(6c)

可将式(6)的解近似表示为

q1(t,ε)=q10(T0,T1)+εq11(T0,T1)+O(ε2)

(7a)

q2(t,ε)=q20(T0,T1)+εq21(T0,T1)+O(ε2)

(7b)

q3(t,ε)=q30(T0,T1)+εq31(T0,T1)+O(ε2)

(7c)

式中T0=t，物理意义为时间t的快变化；T1=εt，物理意义为时间t的慢变化；q10,q20和q30为系统的周期位移，q11，q21和q31为系统的修正位移。

将式(7)代入式(6)并将所得结果按照ε的同阶次展开可得

(8a)

(8b)

(8c)

ε1：

2Vcos(Ωt)

(9a)

(9b)

(9c)

式中D0=∂/∂T0，D1=∂/∂T1。

式(8)为齐次微分方程，其通解可表示为

q10=A1exp(iω1T0)+cc

(10a)

q20=A2exp(iω2T0)+cc

(10b)

q30=A3exp(iω3T0)+cc

(10c)

式中A1，A2和A3为周期位移的振幅(关于T1的函数)，i为虚数单位，cc为共轭项。

首先研究外部激励频率满足Ω≈ω1的 1∶1 主共振情况，引入调谐小参数σ，并令Ω≈ω1+εσ。接着将式(10)代入式(9)可得

Vexp(iσT1)]exp(iω1T0)+

α3A3exp(iω3T0)+

α5{A1A3exp [i(ω1+ω3)T0]+

(11a)

Vexp [i(σT1+iω1T0)]+

β2{A1A2exp [i(ω1+ω2)T0]+

β3{A2A3exp [i(ω1+ω3)T0]+

(11b)

Vexp [i(σT1+ω1T0)]+

(11c)

根据微分方程的可解条件，式(11)有解的充分必要条件为其久期项等于零，即

(12a)

(12b)

(12c)

引入极坐标变换，可将式(12)的A1,A2和A3分别表示为

A1(T1)=0.5ν1exp(iυ1)

(13a)

A2(T1)=0.5ν2exp(iυ2)

(13b)

A3(T1)=0.5ν3exp(iυ3)

(13c)

式中ν1，ν2和ν3为系统的振幅，υ1，υ2和υ3为系统的相位。

将式(13)代入式(12)并分离实部与虚部，进而可得

(14a)

(14b)

(14c)

(14d)

(14e)

(14f)

式中ο1=σT1-υ1。由式(14)可知,ν2与ν3呈衰减趋势，其振动不会受到激发。

求解系统非稳定状态下的解析解不易做到，因此本文只分析系统稳定状态下的动力学行为。对于稳定状态，可令ν1与ο1对时间尺度T1的一阶导数为零，进而消除式(14)的ο1，得到关于ν1的幅频响应方程，即

(15)

同理，可得到当Ω≈ω2+εσ与Ω≈ω3+εσ时系统对应的幅频响应方程，分别表示为

(16)

(17)

4 稳定性分析

根据Lyapunov稳定性理论，稳态解的稳定性可根据式(14)的Jacobi矩阵的特征值来判定。引入坐标变换，使得

ξV=ν1cosο1,ζW=ν1sinο1

(18a,18b)

当Ω≈ω1+εσ时，将式(18)代入式(14a，14b)，进而可得到坐标变换后系统一阶共振的线性化方程，即

(19a)

(19b)

根据式(19)可得Jacobi为

(20)

矩阵J的特征多项式为

det(J-λE)=λ2+Θ1λ+Θ2

(21)

式中E为单位矩阵，λ为特征方程的根，Θ1和Θ2为特征方程根对应的系数，其表达式为

(22a)

(22b)

根据Routh-Hurwitz判据

(23a,23b)

式(23)还可以进一步简化为

Θ2>0

(24)

同理，用类似的方法也可得到Ω≈ω2+εσ，Ω≈ω3+εσ时系统的稳定性判断条件，限于篇幅，本文不再详细赘述。

5 算例分析

悬索的弹性模型E=2.0×1011Pa，初始张力H=4×106N，直径D=0.1385 m，质量m=48.62 kg/m，跨径l=100 m。当F分别为5，10和15时，得到了悬索系统的一阶、二阶和三阶 1∶1 共振的幅值-σ曲线，如图2所示。接着对解的稳定性进行定量判断，图2中幅值-σ曲线的左支和右支的下端是稳定解，右支的上端是不稳定解。

图2 幅值-σ关系

可以看出，系统的 1∶1 共振的幅值-σ曲线具有向右偏移的趋向，表现为硬弹簧特性，存在多值和跳跃现象；当给定同一小参数σ时，一阶共振的幅值远大于二阶和三阶共振的幅值；在同阶次共振的幅值-σ曲线中，左支稳态解的幅值随着小参数σ的增加而增加，右支稳态解的幅值随着小参数σ的增加而减小，非稳态解的幅值一直随着小参数σ的增加而增加；随着F的增加共振产生的幅值有所增加，但悬索系统的振动属于弱非线性振动，因此随着F的增加，幅值的增加是有限制的，并不会存在量级的增加。

图3为 1∶1 主共振的幅值-V曲线，对于σ=0.01，当ν1位于0.11～0.18时，一阶主共振的幅值-V曲线是非稳定的；对于σ=0.02，当ν1位于 0.15～0.255时，一阶主共振的幅值-V曲线是非稳定的；对于σ=0.03，当ν1位于0.19～0.31时，一阶主共振的幅值-V曲线是非稳定的。可以看出，随着σ的增加，临界跳跃点有向右偏移的趋势，且幅值有明显的增加趋势；二阶和三阶主共振的幅值-V曲线与一阶主共振的幅值-V曲线有着相同的变化趋势，但二阶和三阶主共振的幅值-V曲线的幅值比一阶主共振的幅值-V曲线的幅值小许多。

图3 幅值-V关系

为了更清楚地对比一阶、二阶和三阶主共振的幅值-σ曲线与幅值-V曲线的区别，得到了幅值-σ对比分析(F=15)(图4)和幅值-V对比分析(σ=0.03)(图5)。可以看出， 1∶1 主共振发生时，一阶幅值远大于二阶和三阶幅值，即当悬索系统开始振动时，系统的能量主要以一阶模态幅值的形式散发。

图4 幅值-σ对比分析

图5 幅值-V对比分析

中国地域广阔且地形复杂，不同档距的悬索系统适用于不同的地区，因此档距是悬索系统的重要参数，且是变化最多的参数。为分析档距对幅值的影响，图6给出了档距分别为100 m，300 m和500 m时悬索的 1∶1 主共振的幅值-σ曲线，可以看出，随着档距的增加，悬索幅值增加明显，因悬索的振动以一阶模态振动为主，因此一阶共振产生的幅值随着档距的增加最为明显，对于大跨越构件因尽量避免共振的发生。

图6 幅值-σ关系(l =100 m，300 m，500 m)

6 结 论

本文考虑了悬索系统的前三阶模态耦合振动，利用多尺度法分析了悬索系统的共振模式，并基于Lyapunov稳定性理论进行了稳定判定，进而得到如下结论。

(1) 悬索系统 1∶1 主共振的幅值-σ曲线具有向右偏移的趋向，表现为硬弹簧特性，存在多值和跳跃现象，当给定同一小参数σ时，一阶主共振的幅值远大于二阶和三阶主共振的幅值。

(2) 在同阶次 1∶1 主共振的幅值-σ曲线中，左支稳态解的幅值随着小参数σ的增加而增加，右支稳态解的幅值随着小参数σ的增加而减小，非稳态解的幅值一直随着小参数σ的增加而增加。

(3) 在同阶次 1∶1 主共振的幅值-σ曲线中，随着F的增加，共振产生的幅值有所增加，但悬索系统的振动属于弱非线性振动，因此随着F的增加，幅值的增加是有限制的，并不会存在量级的增加。

(4) 悬索系统的幅值-V曲线具有随着σ的增加临界跳跃点向右偏移的趋势，且幅值有明显的增加趋势；二阶和三阶主共振的幅值-V曲线与一阶主共振的幅值-V曲线有着相同的变化趋势，但二阶和三阶主共振的幅值-V曲线的幅值比一阶主共振的幅值-V曲线的幅值小许多。

(5) 随着档距的增加，悬索系统 1∶1 主共振产生的幅值增加明显，因悬索的振动以一阶模态振动为主，因此一阶主共振产生的幅值随着档距的增加最为明显。

附录：

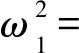
α3=-ϑ5/ϑ1,α4=-ϑ6/ϑ1,α5=-ϑ7/ϑ1

α6=-ϑ8/ϑ1,α7=-ϑ9/ϑ1,α8=-ϑ10/ϑ1

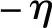
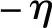
γ3=-δ5/δ1,γ4=-δ6/δ1,γ5=-δ7/δ1

γ6=-δ8/δ1,γ7=-δ9/δ1