基于等效系统假定的变厚度板弯曲广义积分变换解

付光明，庹宇航，李明亮，彭玉丹，孙宝江，张 健

(1.中国石油大学(华东) 石油工程学院，青岛 266580;2.中国石油大学(华东)，山东省油气储运安全重点实验室，青岛 266580；3.中国石油技术开发有限公司，北京 100009)

1 引 言

在实际工程中，除了等厚度板之外，变厚度板已经逐渐受到工程设计人员的重视。在航空航天器、新型船舰及建筑等设计中，变厚度板已经成为一种重要的结构元件。变厚度板相比于等厚度板有助于减轻结构元件的重量，提高材料的利用率。因此，变厚度板力学性质的研究有着重要的意义，变厚度板力学响应问题也引起了国内外学者的关注。

目前，有限元法、有限差分法[1,2]、积分变换法[3,4]和等几何法[5]等算法广泛应用于求解各向同性板和正交各向同性板弯曲问题。李锐等[6]通过辛-叠加方法求解了地基上矩形中厚板的弯曲问题。Heydari等[7]利用变分法优化了厚度呈线性和二次变化的Pasternak双参数弹性地基上圆形功能梯度板的稳定性方程，并利用谱里兹法求解该稳定性方程，进一步讨论了线性、二次厚度变化系数和材料泊松比等对该圆形功能梯度板屈曲的影响。Zenkour[8,9]采用小参数法讨论了机械外力和湿热载荷作用下Levy型变厚度薄板的弯曲问题。Zhang等[10]利用二维广义有限积分变换方法求解了正交各向异性矩形薄板的弯曲解析解。Li等[11]利用有限积分变换法求解了完全夹紧的正交各向异性矩形薄板在任意载荷下的精确弯曲解。Tian等[12]提出了双有限积分变换法来求解弹性地基上各边自由的中厚矩形板的弯曲解析解。

广义积分变换(GITT)是近年发展起来的一种混合数值分析方法[13]，目前该计算方法已广泛应用于求解流动与传热问题[14-16]、固体力学问题[17-20]以及结构振动等问题[21-23]。变厚度板相比于等厚度板其弯曲刚度存在明显的非线性行为，利用广义积分变换方法求解该问题具有明显的优势，目前未见相关的文献报道。本文建立了求解基于等效系统假定的变厚度板弯曲的广义积分变换算法。通过求解满足给定边界条件的辅助方程的特征函数和特征值，利用积分变换方法，将变厚度薄板弯曲问题控制方程变换成常微分方程组并进行求解。将本文计算结果与已发表的结果和有限元数值模拟结果对比，发现本文建立的基于广义积分变换(GITT)的计算结果满足精度要求。利用该算法分析了不同边界条件和载荷分布条件下变厚度薄板的弯曲问题，分析了不同长宽比、边界约束与载荷条件对变厚度板挠度和弯矩的影响规律。

2 变厚度薄板弯曲控制方程

考虑长为a，宽为b的各向同性变厚度矩形薄板，如图1所示。基于小变形假设，横向载荷作用下的变厚度板弯曲控制方程为

(1)

当考虑板厚度t仅沿y方向发生变化，即t=t(y)，则方程(1)可简化为

(2)

式中D=Et3/12(1-ν2)为板的弯曲刚度，ν为泊松比，w为挠度，t为厚度，E为弹性模量。

若变厚度板的厚度t在y方向上满足

t=t0[1+kfN(y)]

(3)

图1 变厚度板

变厚度板弯矩方程为

(4a)

(4b)

为了简化变厚度弯曲控制方程(2)数值求解的复杂性，Fertis等[24-26]提出了基于小参数假定的变厚度板等效系统。根据该假定，厚度沿y方向呈线性和二次分布的弯曲控制方程可简化为

(5a)

(5b)

式中w0为厚度为t0的等厚度板在载荷q作用下的挠度，满足控制方程

4w0=q/D0

(5c)

如图2所示，考虑三种载荷分布形式，即均布载荷UN，q(x,y)=q0，沿x方向线性分布载荷TX，q(x,y)=q0(2x+a)/2a和沿y方向线性分布载荷TY，q(x,y)=q0(2y+b)/2b。同时，考虑六种边界条件，如图3所示，C为固支边界，S为简支边界条件。

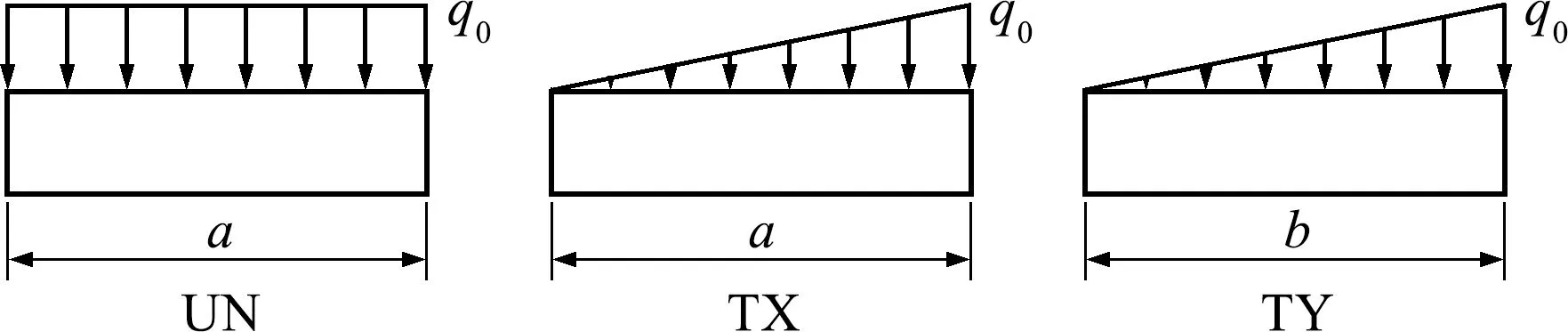
图2 载荷加载

引入无量纲量，

(6)

方程(5)可表示为无量纲形式，

(7a)

(7b)

(7c)

图3 变厚度板边界条件

同理，弯矩方程的无量纲形式为

(8a)

(8b)

式中 当N=1和2时，分别为厚度沿y方向呈线性和二次变化时板内任意点的弯矩。

简支边界条件S和固支边界条件C满足

(9)

3 广义积分变换解的建立

(1) 两端固定边界条件CC

(11)

(12a)

(12b)

(2) 一端简支一端固支边界条件SC

(13)

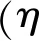
(i=1,2,3，…) (14a)

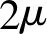
(i=1,2,3，…) (14b)

(3) 两端简支边界条件SS

(15)

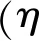
(16a)

μi=iπ/2

(i=1,2,3，…) (16b)

特征向量Yi满足正交特性,

(17)

建立归一化表达式为

(i=1,2,3,…) (18)

建立方程(7a,7b)的积分变换与逆变换如下,

(19a)

同理，方程(7c)的积分变换与逆变换的表达式为

(19b)

将原方程(7)乘以特征函数并在[-1,1]区间积分，利用逆变换公式化简方程，原偏微分方程(7)可转化为常微分方程组形式为

(20a)

(20b)

(20c)

式中

同理，积分变化后的弯矩方程可表示为

(21a)

(21b)

式中 当N=1和2时,分别为沿y方向呈线性和二次变化的变厚度板内任意点弯矩。

考虑ξ方向不同边界条件如下。

两端固定边界条件CC，

(22a)

一端简支一端固支边界条件SC，

(22b)

两端简支边界条件SS，

(22c)

表1 变厚度板挠度弯矩和计算结果及其与文献[8]数据的对比

4 算例与结果分析

表1为等厚度板(N=0)、厚度沿y轴线性(N=1)和二次(N=2)变化的变厚度板中心点处的挠度和弯矩计算结果。该算例中，边界条件为y方向对边固支x方向对边简支(CSCS)边界条件，载荷边界条件为均布载荷(UN)和沿x方向线性分布载荷TX，泊松比为0.3，变厚度系数k=0.2。通过与文献[8]的结果对比，利用GITT方法求得的变厚度板中心处的挠度和弯矩与文献的结果吻合较好。

同时，利用GITT方法计算了不同长宽比、载荷分布(UN、TX和TY载荷)以及边界条件下的变厚度板弯曲问题。图4～图6分别表示在不同边界条件(CCCC，CSCC，CSCS，CSSS，CSSC，SSSS)和载荷分布条件(UN，TX及TY)下变厚度板弯曲挠度的GITT计算结果(ANA.N)和有限元数值模拟结果(FEM.N)的比较，其中，N=1和N=2分别表示变厚度板的厚度沿y轴线性和二次分布。假定泊松比为0.3，变厚度系数k=0.2。可以看出，基于GITT的计算结果(ANA.N)与有限元数值模拟结果(FEM.N)吻合较好。

图4 UN载荷作用下变厚度板挠度与有限元数值模拟结果对比

图5 TY载荷作用下变厚度板挠度与有限元数值模拟结果对比

图6 TX载荷和多种边界下变厚度板挠度与有限元模拟结果对比

5 结 论

本文基于广义积分变换原理，建立了求解变厚度板弯曲问题的广义积分变换法GITT算法。通过与已发表的文献数据和有限元数值模拟计算结果比较，证明建立的GITT方法具有较高的计算精度。利用建立的广义积分变换法算法分析了线性和二次变化的变厚度板在均布载荷UN、载荷沿x方向和y方向线性分布条件下的挠度和弯矩值，同时讨论了不同边界约束条件和长宽比等几何特征对中心点处挠度的影响规律，计算结果可为实际工程计算提供参考。

本文以厚度沿y方向变化为例建立了求解的变厚度板弯曲问题的GITT模型，该方法同样适用于求解厚度沿x和y两方向变化以及任意载荷作用下的变厚度板弯曲问题。