带有障碍物溃坝流动问题的有限元数值模拟研究
高普阳, 杨 扬
(1.长安大学 理学院,西安 710064;2.西北工业大学 航空学院,西安 710072)
1 引 言
溃坝流动问题出现在海洋工程、水动力学和泥石流滑坡等诸多领域,该过程会遇到运动界面的翻转、飞溅及破碎等大变形情况,一直都是学者们关注的热点问题[1-5]。
溃坝坍塌流动过程会涉及到牛顿或者非牛顿流体和空气之间的相互作用,可以将其视为两相流动问题。王吉飞等[6]采用Level Set方法追踪运动界面,并通过SUPG格式数值求解Level Set方程。对于Navier-Stokes方程的求解,则在FEM中加入了SUPG和PSPG的稳定化方法。Issakhov等[7]依据流体体积函数法捕捉运动界面,以保证流体的质量守恒性,并考虑了湍流模型。以上学者们的研究仅限于牛顿流体。
自然界中诸多流动现象也常涉及到非牛顿流体,Cremonesi等[8]研究了宾汉非牛顿流体的溃坝流动过程,并模拟了泥石流现象。采用显式粒子有限元方法数值求解了拉格朗日形式的Navier-Stokes方程,但是并没有考虑下游带有障碍物的非牛顿流体溃坝流动情况。目前对于非牛顿流体溃坝流动问题,特别是下游带有障碍物情形的研究鲜有报道。
Level Set方法可以简单和有效地追踪运动界面,但其最大的缺陷就是容易引起流体的质量误差。Yu等[9]采用CLSVOF方法模拟了带有障碍物的溃坝流动,通过Level Set方法追踪运动界面,同时利用VOF方法对流体质量进行追踪,以保证良好的质量守恒性,但这时需要另外求解VOF输运方程。Level Set方程属于对流型方程,直接采用标准有限元方法求解时,容易引起数值振荡现象。Touré等[10]将Level Set方程转化为一个带有参数的对流-扩散方程,并采用稳定化SUPG方法进行空间离散,但这会产生一些额外的数值误差。间断有限元方法在求解双曲型方程时具有诸多优点[1,5],因此本文采用了间断有限元方法对Level Set 方程进行求解,以保证计算过程的稳定性和数值精确度。
本文主要目的是基于两相流动模型,在有限元算法框架下,数值模拟研究带有障碍物的牛顿和非牛顿溃坝流动问题。对于自由界面的追踪,采用简单和有效的Level Set方法,并引入了一个质量矫正技术,以保证长时间计算以及界面大变形过程中的流体质量守恒性。另外,本文在控制方程中加入了幂律型本构模型,用以描述非牛顿流体的流动特性。通过基于分裂格式的SUPG稳定化有限元算法求解统一的Navier-Stokes方程,并采用间断有限元方法求解双曲型Level Set及其重新初始化方程。
2 数学模型
2.1 Level Set方程

随着时间发展,Level Set函数值会根据速度进行更新。对于不可压缩流体,守恒形式的Level Set方程为

(1)
为了保证计算过程中Level Set函数的符号距离函数特性,需要求解如下的Level Set重新初始化方程[12],即
(2)

2.2 统一的Navier-Stokes方程
溃坝流动中会涉及到两种不同的流体,为了求解方便,本文将整个流场控制方程写成统一形式为
(3)
∂u/∂+(u·)u=-p+(1)·
{μ[u+(u)T]}+(1)f
(4)
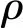
(5)
2.3 幂律型本构模型
根据流变学理论,非牛顿流体的粘度会受到剪切速率变化的影响。本文采用幂律型本构模型[13]描述剪切应力和形变速率之间的非线性关系,应变率张量定义为d=[u+(u)T]/2,量级γ定义为对于幂律型本构模型,粘度与应变率张量的关系为
μl=μlγn - 1
(6)
式中n为幂律指数。n=1时,该模型表示牛顿流体;n<1时,该模型表示假塑性非牛顿流体;n>1时,该模型表示胀塑性非牛顿流体。
3 统一Navier-Stokes方程的数值求解
3.1 分裂格式及时间离散
对于统一Navier-Stokes,本文采用Euler向前格式进行时间离散,对于非线性对流项和表面张力项进行显式处理,并隐式处理压力项和粘性项。这样,可以得到半离散格式
(7)
本文采用分裂格式,首先忽略方程(7)右端的压力项和粘性项,得到双曲型子方程
(8)

(9)
(10)
根据pn + 1,就可以计算中间速度
(11)
最后,可以得到关于速度的Helmholtz方程为
(1/ρ)·{μ[un + 1+(un + 1)T]}+(1/Δt)un + 1=

(12)
将分裂所得的子方程 (8,9,12)叠加,就可以得到半离散方程(7)。
3.2 空间离散
本文采用Ωh表示对求解区域Ω进行正则三角剖分,Ωi(i=1,2,…,N)代表网格上的小三角形,有限元空间可以定义为
Ck(Ωh)={v∈C0(Ω)∀Ωi∈Ωh,v|Ωi∈Pk(Ωi)}
(13)
式中Pk(Ωi)为Ωi上不低于k次的多项式。
对于双曲型子方程(8),采用SUPG方法[14]进行空间离散,对方程两边同时乘以试探函数。u速度分量方程的具体形式为
(14)

另外的几个子方程均属于椭圆型方程,因此采用标准FEM进行空间离散。方程(10)的空间离散形式为
(15)
类似的,可以得到方程方程(11,12)的空间离散格式。
4 Level Set方程的数值求解
在求解Navier-Stokes方程得到速度后,就可以进一步求解Level Set方程以更新运动界面的位置和形态。对于Level Set方程(1)的时间离散,采用向前Euler格式

(16)
由于Level Set方程(1)属于双曲型方程,因而本文采用稳定和有效的间断有限元方法进行空间离散。首先在之前网格三角剖分的基础上,定义间断有限元空间为
Dk(Ωh)={l∈L2(Ω)∶∀Ωi∈Ωh,l|Ωi∈Pk(Ωi)}
(17)
另外,Lax-Friedrichs数值通量f*可以定义为
(18)
在方程(18)两端同时乘以试探函数lh,并关于对流项做两次分部积分,可得
(19)
(20)
类似的,可以得到Level Set重新初始化方程的全离散格式。计算过程中时间步长的选取依据为
(21)
5 质量矫正技术
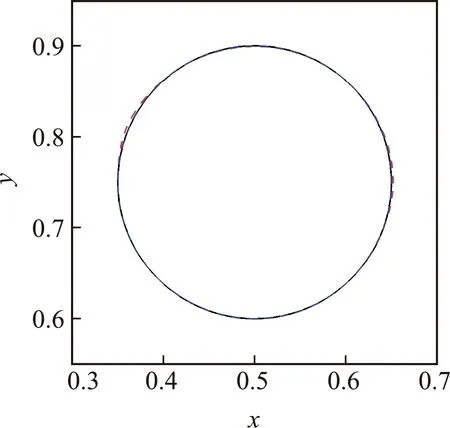
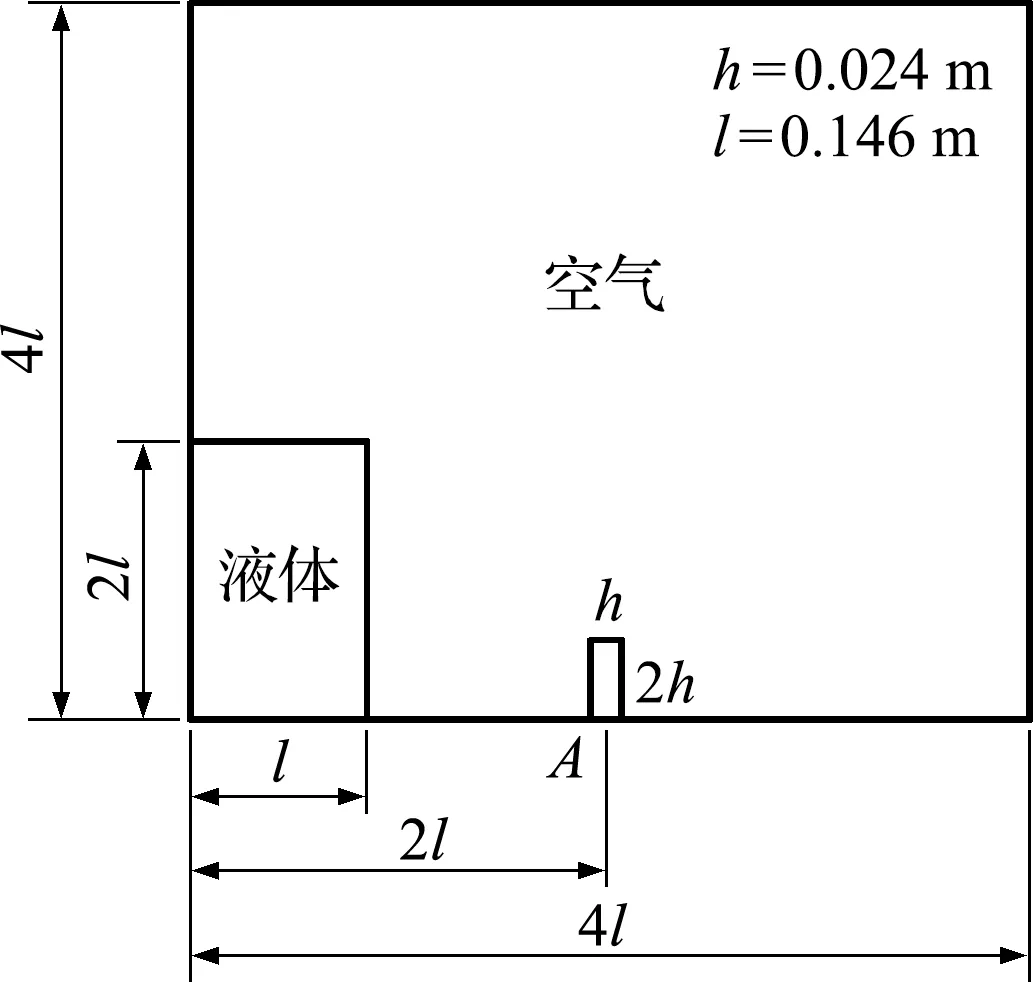
为了保证流体的质量守恒性,在整个求解过程中加入了一个简单的质量矫正技术。如图1所示,假设现在计算得到的运动界面为G,这时得到的液体质量为S,而真实的流体质量为Se。S与Se之间可能会存在一个比较小的误差(假设S (22) (23) 图1 质量矫正技术 根据前面发展的耦合算法,数值模拟研究牛顿、非牛顿溃坝流动问题以及下游带有障碍物的情形,所有的数值模拟均是基于Freefem++[15]开源计算平台进行。 首先研究单涡剪切流动问题,用来验证数值方法较好的质量守恒性。初始时刻圆心所在位置为(0.5,0.75),圆的半径为0.15,整个计算区域为[0,1]×[0,1]。速度场设定为[16] u=-sin2(πx)sin(2πy),v=sin2(πy)sin(2πx) 在t=1时,将整个速度场进行翻转。因此,理论上单涡会在t=2时回到其初始位置。计算时分别采用了两套规则的三角形网格1(Δx=Δy=1/100)和网格2(Δx=Δy=1/100),时间步长均取为Δt=0.001。 图2中黑色实线、红色虚线以及蓝色虚线分别表示t=2时的精确解以及Mesh 1和Mesh 2上的数值解。在Mesh 1和Mesh 2上得到数值结果的相对质量误差分别为1.1%和0.5%,验证了数值算法较好的质量守恒性。可以看出,数值解具有很好的网格收敛性,而且和精确解吻合较好。 图2 t =2时刻精确解和数值解的比较 图3 下游带有障碍物溃坝流动问题示意图 初始时刻,液柱右侧会有一个挡板,当瞬间抽走这个挡板时,液柱会在重力的作用下发生坍塌,向右下方流动。整个流动过程由于中间障碍物的存在,液体前沿界面会发生碰撞和飞溅等大变形现象。 计算过程中用到了三套逐次加密的非结构网格,网格1,2和3的最大网格尺寸分别为1/100,1/120和1/150,求解区域内的小三角形单元数分别为8983,13386和20539,图4(a)给出了计算过程用到的网格2。本文所有的数值模拟中,时间步长均取为0.0002。图4(b)展示了三套计算网格上,t=0.2 s时的前沿界面形态。其中,红色、黑色和蓝色线条分别表示在网格1,2和3上计算得到的数值结果,可以看出,耦合算法具有很好的网格收敛性。为了保证数值结果的精确性并减少计算量,后续的数值模拟均在网格2上进行。 图4 计算用的网格2及三套计算网格上t =0.2 s时的界面形态 图5给出了在网格2上计算得到的(t=0.1 s,0.3 s和0.5 s)液体的界面位置和形态。本文数值结果和实验结果均吻合较好,这验证了耦合算法的可行性以及准确性。整个流动过程中,流体质量的最大误差为1.2%,证明了耦合算法较好的质量守恒性。本文数值模拟结果的最大相对质量误差,要比文献[10]稳定化有限元方法计算得到的最大相对质量误差小一些。 图5 不同时刻牛顿流体的前沿界面形态 图6(a)给出了左侧边界上流体高度随时间的变化,图6(b)给出了障碍物左下角(点A)处的压力随时间的变化。当液柱坍塌下来冲击到障碍物左下点时,该点的压力瞬间增加,峰值约为6000 Pa。可以看出,本文的数值结果和文献[7]几乎一致,进一步验证了数值算法的准确性。表1给出了若干时刻障碍物左下角(点A)处液面的垂直高度。 图6 左边界上液面高度及障碍物左下角(点A)处的压力随时间的变化 表1 障碍物左下角(点A)处若干时刻液面的垂直高度 图7给出了若干时刻液体的前沿界面形态,其中浅灰色表示本文的计算结果,深灰色表示文献的计算结果。 图7 流体前沿界面形态 另外,图8进一步展示了液体前沿界面位置随着时间的变化曲线。可以看出,本文的数值结果和文献[8]已有的计算结果以及实验结果[18]均吻合得很好,这验证了数值算法处理非牛顿流体溃坝流动的准确性。 图8 x轴上液体前沿界面位置 继续研究非牛顿流体的溃坝流动情况,整个求解区域及边界条件和6.2节一致,所有的数值模拟均在图4给出的网格2上进行。首先考虑n=0.5时的假塑性非牛顿流体,图9给出了若干时刻液体的自由运动界面形态,可以看出,这时前沿界面相比于图5的结果更为紊乱一些,尤其是在和右壁面碰撞之后,液体的飞溅和破碎现象更加明显,这些都是因为随着流动速度的增加,假塑性非牛顿流体的粘度会变小,更容易发生形变。 图9 假塑性流体(n =0.5)溃坝流动中若干时刻的运动界面形态 进一步,图10给出了障碍物左下角(点A)处压力的变化曲线,可以看到其峰值约为6600 Pa,较高于6.2节的情况。另外,流动过程中,流体质量的最大相对质量误差为1.5%。 接着,本文进一步考虑n=1.5时的胀塑性非牛顿流体,图11展示了若干时刻流体的运动界面形态,相比于图5和图9的结果,这时的前沿界面更加光滑。这是因为胀塑性非牛顿流体在速度增加时,粘度会变大,不容易发生飞溅和破碎等现象,与文献[8]的描述一致。图12展示了障碍物左下角(点A)处压力随时间的变化曲线,压力峰值约为4200 Pa,相比于牛顿流体和假塑性非牛顿流体,该值都要低很多。此外,流动过程中,液体的最大相对质量误差为0.8%。 图10 障碍物左下角(点A)压力随时间的变化 图11 胀塑性流体(n =1.5)溃坝流动中若干时刻的运动界面形态 图12 障碍物左下角(点A)压力随时间的变化 本文基于两相流动模型,采用Level Set前沿界面追踪方法,在有限元框架下数值模拟研究了下游带有障碍物的牛顿和非牛顿溃坝流动问题,并分析了不同特性流体自由界面的发展形态。 对于牛顿流体,本文数值模拟结果和文献已有报道均吻合得很好,这表明本文耦合算法具有较高的准确性。对于非牛顿流体,数值结果表明,假塑性流体对于障碍物的最大冲击力最大,而且在流动过程中液体界面最容易出现破碎和飞溅等大变形现象;胀塑性流体对于障碍物的最大冲击力最小,在整个流动过程中界面最为稳定和光滑。整个流动过程均保证了较好的质量守恒性,所有模拟结果中最大的质量误差为1.5%。剪切变稀的非牛顿流体在溃坝流动问题中,对于下游障碍物的破坏性最大。因此,当实际问题涉及到这类流体物质时,需要注意对下游障碍物的加固,防止流体将障碍物冲垮。


6 数值算例
6.1 单涡剪切流动
6.2 带有障碍物的牛顿流体溃坝流动
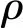




6.3 非牛顿流体溃坝流动
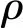


6.4 带有障碍物的非牛顿流体溃坝流动




7 结 论

