基于态型近场动力学的准静态数值仿真方法
孙璐妍,余 音,郑晓玲
(1.上海飞机设计研究院,上海 201210;2.上海交通大学 航空航天学院,上海 200240)
1 引 言
2000年,Silling[1]提出了一套能够求解多尺度不连续力学问题的近场动力学理论,其优势得益于借助相同的数学模型描述物体从原子尺度到宏观尺度的力学行为。它是在空间域中将对象离散为一系列物质点,物质点之间通过非局部作用产生联系,物质点的运动由空间积分方程表达,可以使用统一的数学模型求解多尺度力学行为,突破了空间微分方程及连续性假设的瓶颈,不连续现象随求解自然发生[2]。
Silling等[3]提出的态型PD理论利用物质点间的力状态和变形状态来构造本构关系,物质点之间相互作用力和相对变形分解成和传统力学概念类似的各向同性量和偏量,周围环境对物质点的影响通过各向同性量表达,PD模型参数和传统材料力学参数通过能量推导建立关系,弥补了早期键型PD理论无法正确反应某些材料属性的不足。Silling[4]又推导了态型PD线性化理论,得到了模量状态。在Silling的指引下,态型PD理论推广应用于瞬态动力学问题的求解[5]、弹塑性[6]和准脆性断裂特征[7]本构模型的描述。态型PD理论相应的计算体系也进一步完善,如特定条件下计算塑性变形的隐式算法[6]、态型PD材料失效判别准则[8]和影响非局部作用的权函数设定[9]等。
真实的薄壁结构往往存在钉孔连接等疲劳细节,而失稳是薄壁结构主要的失效模式之一,PD理论为后续研究失稳对疲劳细节裂纹萌生与扩展的影响开辟了一条新路。动力松弛法是一种借助带临界阻尼的动力学方程求解静力学问题的方法,尤其适用于材料和几何非线性问题的求解。Kilic等[10]以键型PD理论为基础,运用动力松弛法求解了轴压屈曲和热屈曲问题。
本文将在态型PD线性化理论基础上,推导节点刚度矩阵和结构刚度矩阵的表达关系,改进 Kilic 等[10]基于键型PD理论的动力松弛法,构建态型PD理论中准静态仿真的数值计算方法,并将该方法用于金属矩形薄板的轴向压稳定性预测。使用合理的离散方法建立薄板的态型PD模型以提高计算速率,通过矩形薄板拉压的基准数值实验与有限元仿真结果对比,验证薄板态型PD模型的正确性。最后,本文通过经验公式证明了金属平板轴压稳定性仿真结果的可靠性。
2 态型PD理论简介
2.1 基本理论
假设物体占据某一空间域R,线性化态型PD理论[4]将域内物质点x的运动方程描述如下,
P(x)u(x,t)+b(x,t)
(1)
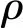
2.2 节点刚度矩阵与结构刚度矩阵
设结构离散后,节点总数为N,有Nx个节点qi(1≤i≤Nx),满足|qi-x|<2δ,将式(1)的积分展开,得到节点x的增量平衡方程如下,
(2)

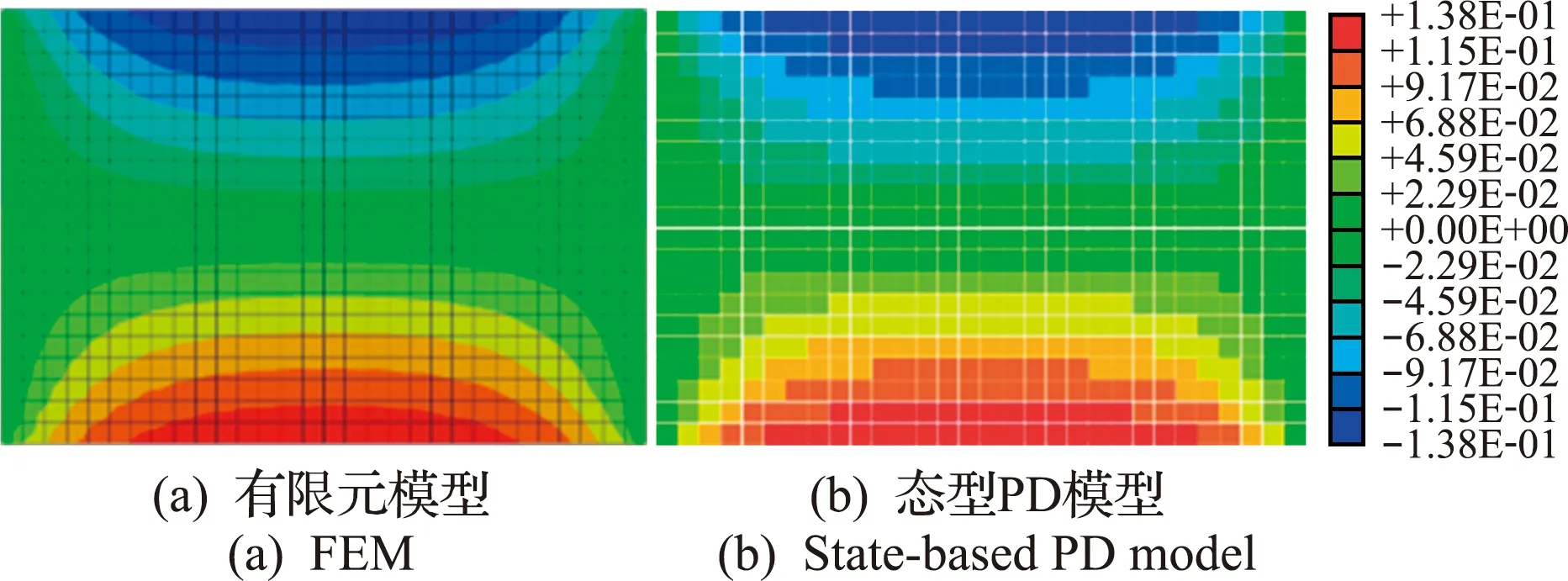
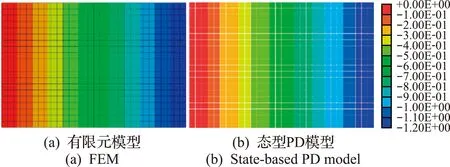
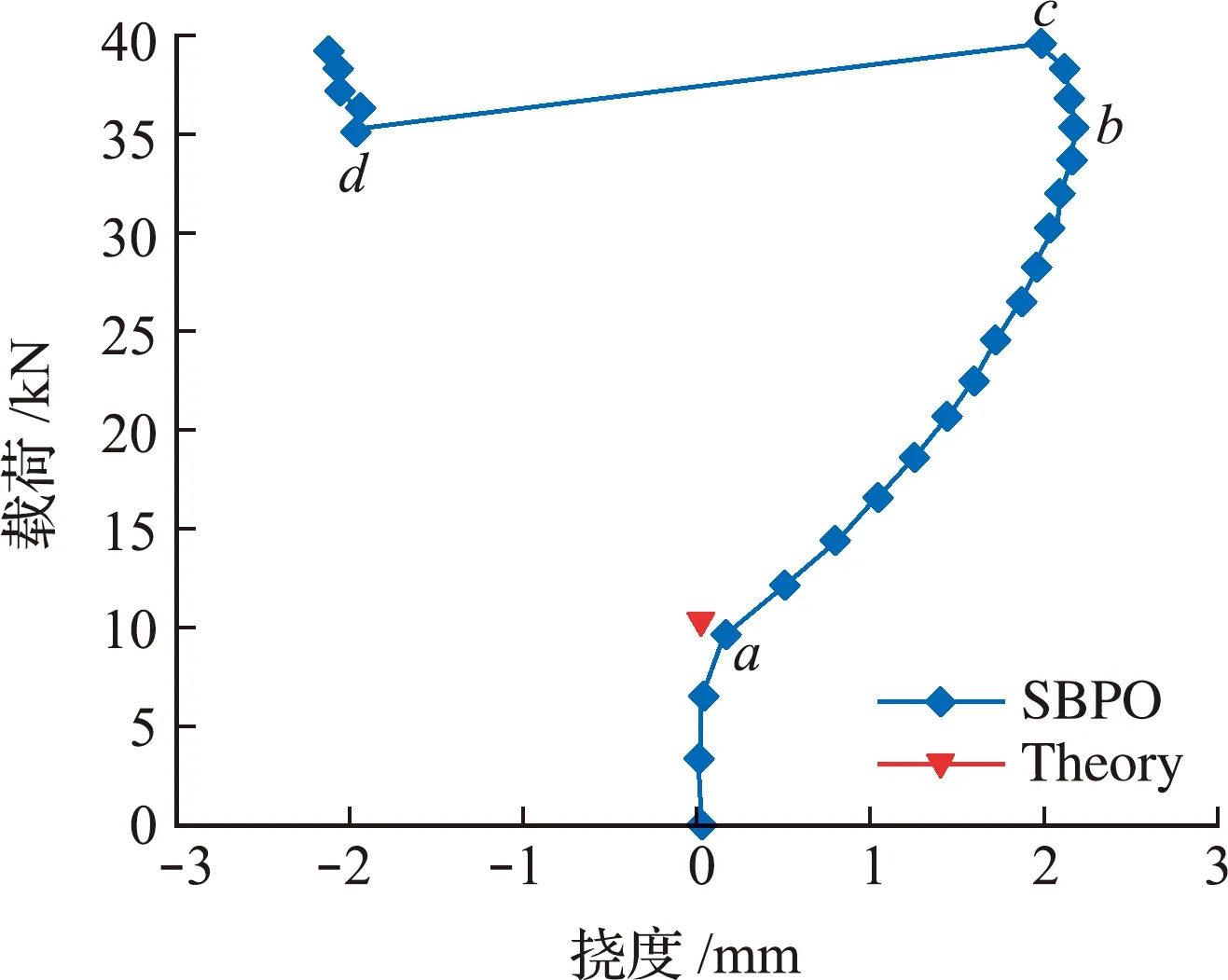
从零开始编号,xi(0≤i (0≤i 式中Ci j=C(xi,xj),uj=u(xj),bi=b(xi),结构刚度矩阵具有对称性[4]。 按照达朗贝尔原理,建立节点x的运动方程为 (t=nΔt) (4) 虚拟阻尼一般不高于系统临界阻尼系数,cn(x)为对角矩阵,对角元素取值如下, (6) 将式(4)进行有限差分写成分量形式即为 (7) t+Δt时刻节点的位移为 初始位移场的选择直接影响到算法的收敛速度,故节点的初始位移根据节点空间位置插值得到。 本文选取的初始位移场引起的系统不平衡力较小,在进行系统平衡判定时,若选用绝对不平衡力收敛准则,则迭代次数过少影响求解精度,若选用相对不平衡力收敛准则,则迭代次数过多影响求解速度。本文融合了相对及绝对两种准则的优势,得到了一种修正的收敛准则为 (8) 本文分析借助了结构分析软件SBPD(State -Based Peridynamics),软件求解器基于VC++语言,通过统一计算设备架构技术CUDA(Compute Unified Device Architecture)和共享存储并行编程语言扩展OpenMP(Open Multi-Processing),提供了CPU+GPU协同和CPU多核两种并行计算方式。 以矩形薄板拉压作为基准试验,将SBPD与ABAQUS的仿真结果进行对比。矩形薄板长为 300 mm,宽为200 mm,厚为2 mm,弹性模量为 69 GPa,泊松比为0.33,载荷形式为沿长度方向的位移。平板拉伸的边界条件为双边简支,双边自由;压缩的边界条件为四边简支。拉和压施加的位移大小均为1.2 mm。 在PD理论的数值仿真中,物体通常划分成大小一致的正方体晶格,节点设在晶格的正中,对于薄板问题,若厚度方向只划分一层晶格,会使节点刚度矩阵中与厚度方向有关的量为0,导致方程无法求解,不仅如此,薄板结构发生屈曲时,面内的应力应变在厚度方向上是变化的,因此在厚度方向上至少划分两层晶格。而薄板结构的长宽方向的尺寸远大于厚度方向的尺寸,正方体晶格的离散方法会导致模型节点的数量过于庞大,影响求解效率。本文将结构离散成方板晶格,在板厚方向划分了两层晶格,晶格长宽为10 mm,厚为1 mm,晶格数量为1200,方板晶格的对角线长为14.2 mm,即为节点的近场范围,节点2倍近场范围内一般有49个节点与之关联。与之相比,常规离散方法至少需要划分120000个正方体晶格,节点2倍近场范围内一般有73个节点与之关联,节点刚度矩阵计算需要经过两次关联节点的遍历,其计算时间与关联节点数量的平方正相关,整个模型的求解时间与节点数量和节点刚度矩阵计算时间正相关。综上所述,本文方法将求解效率提升了约200倍。 在ABAQUS中做了类似的离散处理,单元类型为三维实体减缩积分单元C3D8R。分析得到的平板拉伸沿y方向的位移场云图如图1所示。 ABAQUS得到的拉压外力值分别为112.2 kN和-124.6 kN,SBPD得到的拉压外力值为119.9 kN和-131.9 kN,SBPD的结果比ABAQUS大6%~7%。这是由于两者离散方法的差异造成的,PD模型的实际加载端距为290 mm,相同的位移载荷下,需作用的外力也更大,因此两者结果差异的趋势也是合理的,证明了金属矩形薄板态型PD模型的正确性。 图1 平板拉伸沿y方向的位移场云图(单位:mm) 图2 平板压缩沿x方向的位移场云图(单位:mm) 对于对称结构而言,数值仿真稳定性问题需要先引入初始几何缺陷作为扰动,本文引入的初始缺陷形态为ABAQUS屈曲分析的第1阶模态位移场,设置的缩比因子为0.2(幅值大小为1/10的平板厚度)。 仿真得到的轴向载荷位移变化曲线如图3所示,可以看出,平板在点a发生了初始屈曲,载荷为9.6 kN,轴压刚度突变,与初始值比下降了40%,此时平板仍然具有承载能力;初始屈曲后轴压刚度缓慢降低,在点b发生了二次分支型屈曲,载荷为35.2 kN,此时的平衡状态并不稳定;很快在点c发生了三次跳跃型屈曲,载荷为39.6 kN,在点d达到新的平衡状态,从点c到点d的过程中,平板的轴压刚度突变,出现不连续跳跃,点c和点d的轴压刚度分别约为初始值的40%和30%;此后平板继续承载,面内刚度保持缓慢下降。平板中心点挠度随载荷变化的曲线如图4所示,屈曲模态变化如图5所示,可以看出,屈曲前中心点挠度变化很小,初始屈曲后迅速变大,在中心区域出现一个半波波形,半波慢慢鼓起,在波峰挠度无法继续变大时,发生二次屈曲,一个半波扩展为两个方向一致的半波,然而这个状态并不稳定,迅速发生三次屈曲,中心点挠度发生了突变,在两个波之间出现第三个方向相反的半波。 图3 载荷位移曲线 图4 中心点挠度随载荷变化的曲线 图5 屈曲模态 常用的矩形平板压缩稳定性临界应力σc r公式[11]如下, (9) 式中 杨氏模量E取69×103MPa,泊松比μe取 0.33,平板厚度δ取2 mm,加载边宽度b取为 200 mm,压缩临界应力系数Kc与平板长宽比和边界约束有关,对于本文问题,Kc取4,计算得到σc r=25.47 MPa,乘以加载边截面面积得到临界压力10.190 kN,数值仿真结果与该值相差约5.7%,证明仿真得到的初始屈曲结果是可靠的。 从仿真结果可知,矩形平板初始屈曲后仍具备一定的承载能力,且三倍初始屈曲载荷内,平板的屈曲模态形式不会发生变化,这与矩形薄板轴压稳定性的试验研究成果一致[12,13]。试验研究发现金属矩形薄板是否发生多次屈曲与矩形薄板的长宽比和边界条件有关,而最终破坏与金属材料进入塑性状态有关[13]。 本文提出了一种基于PD状态理论准静态问题仿真的数值方法。 (1) 针对PD薄板模型提出了合理的离散方法以提高计算效率。 (2) 推导了节点刚度矩阵和结构刚度矩阵的表达关系,改进了Kilic[9]基于PD键理论的动力松弛法。 (3) 结合绝对准则和相对准则,提出了一种新的修正迭代收敛准则,并将该方法成功运用于薄板拉压及轴压稳定性的数值仿真中。 目前,态型PD理论的研究工作还处于起步阶段,相信待理论框架和计算体系成熟之后,将在不连续力学领域发挥更大的作用。3 准静态问题的数值方法



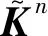
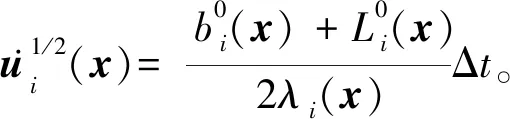

4 数值仿真
4.1 基准数值试验
4.2 金属平板轴压稳定性分析


5 总 结

