基于贝叶斯支持向量回归机的自适应可靠度分析方法

汪金胜，李永乐，杨 剑，徐国际*

(1.西南交通大学 土木工程学院，成都 610031；2.中南大学 土木工程学院，长沙 410075)

1 引 言

工程结构在建设和服役期内不可避免地存在各种不确定性因素，如荷载条件、材料性质和环境因素等。在这些不确定性因素作用下结构系统的响应也表现出一定的随机性。因此，在结构分析过程中，合理考虑随机因素的影响对于结构的安全性评估和相应的决策分析至关重要。作为不确定性量化分析领域的一个重要分支，可靠度理论为考虑上述不确定性因素提供了一条有效的途径[1]。结构可靠度分析的主要目的是计算结构在一定极限状态下发生失效的概率Pf。国内外学者对此进行了大量的研究，并提出了许多近似分析方法[2-7]。近年来，以代理模型为基础的一系列可靠度分析方法因能有效地平衡计算精度和计算效率而得到大量研究和越来越广泛的应用[8]。该类方法通过少量的训练样本(模型计算)建立原问题的代理模型来进行结构可靠度分析，可以在保证失效概率计算精度的前提下显著提高计算效率。常用的代理模型包括响应面法(RSM)[9,10]、人工神经网络(ANN)[11]、支持向量机(SVM)[12]和Kriging模型[13]等。其中，以基于Kriging模型为代表的主动学习算法因在精度和效率之间优异的折中性逐渐成为可靠度领域一个热门的研究课题。此类算法利用代理模型提供的预测值和局部误差估计(如Kriging的预测方差)构建学习函数，在迭代过程中自适应地选取新的重要样本点对模型进行更新，直至满足设定的收敛条件[13]。相关的研究重点可概括为以下几个方面。(1) 构建高效学习函数，如U函数、EFF函数、H函数、FNEIF函数和REIF函数等[14]； (2) 推导收敛准则，如基于相对误差估计的收敛准则及其改进策略[15-17]； (3) 提出有效抽样区域概念，如自适应抽样域法[18]； (4) 高效混合算法计算小失效概率，如基于Kriging和重要抽样的方法[19]以及基于Kriging和子集模拟的方法[20]等； (5) 解决系统失效概率计算[21,22]和结构优化设计[23]等问题。

目前，大多数自适应学习算法都是基于Kriging模型建立的，而基于其他代理模型的学习算法相对较少。这主要是因为Kriging模型不仅能得到新点的预测值，而且还能给出其局部误差估计，为高效地构建主动学习算法提供了便利；而传统的支持向量机等其他代理无法直接得到预测方差，需要额外采用Bootstrap等方法才能得到近似误差估计，计算比较繁琐。针对此问题，一些学者在贝叶斯推理框架下进行代理模型的构建，如近期提出的贝叶斯稀疏混沌展开(Bayesian sparse PCE)[24]和贝叶斯支持向量回归机(Bayesian SVR)[25]。与Kriging模型类似，Bayesian sparse PCE模型和Bayesian SVR也能直接得到预测方差值，因此现有的主动学习算法可直接适用于贝叶斯推理框架下的PCE模型和SVR 模型。不过，与基于经验风险最小化原则建立的PCE和ANN等模型不同的是，SVR模型采用结构风险最小化原则进行构建，具有严格的理论基础和良好的泛化能力，有效地避免了过拟合，且能很好地处理小样本、高维度和非线性等问题。因此，基于Bayesian SVR模型建立的自适应学习算法有望进一步提升该类算法的有效性和适用性[26]。

鉴于此，本文提出一种新的基于贝叶斯支持向量回归机的高效自适应学习算法(ABSVR)用于结构可靠度分析。首先，借鉴优化算法中惩罚函数的概念，提出了一种新的学习函数。该学习函数综合考虑了样本点的预测值、预测方差、概率密度函数值以及与已有样本点的距离等因素，能有效地引导算法在学习过程中选取位于极限状态曲面附近且对失效概率贡献大的样本点。其次，考虑到失效概率估计的特点，提出了一种新的有效抽样域策略，以筛选出对失效概率计算误差贡献大的点作为备选样本点，提高算法的学习效率。此外，为确定合适的收敛准则，防止因欠学习产生较大估计误差或过学习产生冗余样本而降低计算效率，本文引入一种基于相对误差估计的停止条件，确保算法在达到给定误差阈值的情况下自动停止。最后，通过三个算例验证本文所提方法的适用性、准确性和高效性。

2 贝叶斯支持向量回归机

支持向量机最初是由Vapnik等[27]在统计学习理论指导下提出的用于解决模式识别问题的算法，之后进一步推广到函数回归分析中，并在不同领域得到了广泛应用。为进一步提升支持向量回归机的构建效率和性能，文献[25，28]在贝叶斯推理框架下采用不同的损失函数建立了支持向量回归机(Bayesian SVR)模型。考虑到不同Bayesian SVR模型性能的相似性，本节仅对文献[26]中基于平方损失函数(式(1))构建的Bayesian SVR进行简要介绍，并用于后续自适应可靠度分析算法的建立。

(1)

2.1 贝叶斯推理框架

给定由输入变量点集X={x1,x2,…,xN}T和相应的结构响应Y={y1,y2,…,yN}T组成的训练样本集D={(X,Y)|xi∈n,yi∈(i=1,2,…,N)}，则在回归分析中训练样本对关系为

(i=1,2,…,N)(2)

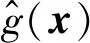
(3)

式中λ为待求常数,l(δ)为式(1)的损失函数。

(4)

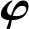
(5)

式中Σ为大小为N×N的协方差矩阵，每个矩阵元素可通过式(4)得到。此外，由于δi为服从独立同分布的变量，给定训练样本集下的似然函数为

(6)

根据贝叶斯理论，g的后验概率分布为

(7)

式中P(D|φ)为归一化常数。将式(5,6)代入式(7)可得

(8)

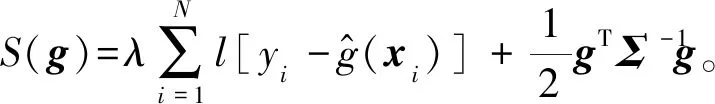
(9)

2.2 Bayesian SVR模型

针对模型采用的平方损失函数，文献[25]推导出了式(9)中g的最优估计值为

(10)

式中I为大小为N×N的单位矩阵，β=(Σ+I/λ)-1Y。对于Bayesian SVR模型中涉及的超参数φ={θ,λ}，可通过求解极小值问题(11)得到。

(11)

(12)

(13)

式中κ(x,X)=[κ(x,x1),κ(x,x2),…,κ(x,xN)]T，可由式(4)计算得到。

至此，在贝叶斯推理框架下建立了Bayesian SVR模型，得到的预测值和预测方差的表达式可直接用于构建结构可靠度分析的自适应算法。关于该模型更详细的推导过程和基于其他损失函数建立的模型参见文献[26,29]。

3 ABSVR算法

本文将Bayesian SVR模型用于自适应学习算法(ABSVR)的建立，主要从三个方面提升其整体性能，一是基于可靠度分析中重要样本点的特征，利用优化算法中惩罚函数的概念，提出一种新的高效学习函数；二是构建有效抽样域，选取对失效概率估计误差贡献大的点作为备选样本点；三是引入一种基于相对误差估计的停止条件，防止因欠学习或过学习而降低算法性能。

3.1 学习函数

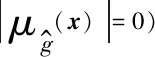
(14)

学习函数U能有效表征样本点在代理模型中错误分类的概率，即

Pw=Φ[-U(x)]

(15)

式中Pw为样本点的错误分类概率，Φ(·)为正态分布累积概率密度函数。由式(15)可知，函数U值越小，样本点属性错误分类的概率就越大。因此，文献[13]采用函数U的极小值作为选点策略，

(16)

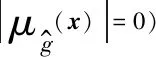
(1) 利用优化算法中惩罚函数的概念，构建函数式为

(17)

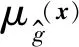
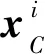
(18)

因此，综合考虑以上各种因素的影响，本文提出一种新的学习函数(NLF)，其表达式为

(19)

式中γ为常数，可防止式中分母为零，本文取γ=1×10-5；max(·)为一簇x∈SC对应估计值的最大值。学习过程中，选取备选样本集SC中使学习函数NLF(x)最小的点xnew加入现有样本集SD中，即

(20)

本文通过学习函数NLF和Bayesian SVR模型构建的自适应算法记为ABSVR2。为选取更具代表性的样本点，备选样本集SC的点应具有较好的空间满布性和均匀性。因此，将利用UQLab[30]抽取Sobol序列作为样本集SC的点。

3.2 有效抽样域

由式(15)可知，位于极限状态曲面附近或预测方差大的点错误分类的概率更大，是失效概率估计的主要误差来源，因而在自适应学习过程中需重点关注该区域内的样本点。其中，错误分类的情况有两种，一是属于安全域内的点以一定的置信度(如95%)误分为失效点，该类点记为SS；二是属于失效域内的点以一定的置信度误分为安全点，该类点记为SF。这两类样本点主要分布在极限状态曲面附近区域，可分别表示为

(21)

(22)

3.3 收敛准则

收敛准则在自适应学习算法中十分重要，为使算法能更好地在计算效率和精度间达到平衡，需要设置合适的停止判据，否则过学习和欠学习都可能使算法的性能大打折扣。常用的方法是，给学习函数设定一个阈值，当满足阈值条件时停止学习，如文献[13]中针对学习函数U的收敛准则。然而，此类准则可能过于保守，导致不必要的计算开销，而且合适的阈值有时很难确定。为此，一些学者提出了基于相对误差估计的收敛准则[15-17]，将停止条件与失效概率估计误差联系起来，可在保证精度的前提下减少功能函数的调用。本文采用文献[17]的方法建立ABSVR1和ABSVR2的收敛条件。

(23)

(24)

(25)

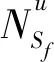
(26)

因此，给定误差阈值εt，相应的收敛准则为

εr≤εmax≤εt

(27)

3.4 ABSVR算法基本流程

根据3.1节～3.3节的阐述，本文所提ABSVR算法用于结构可靠度分析的主要步骤如下。

(1) 从Sobol序列中抽取NC个样本点组成备选样本集SC；利用拉丁超立方抽样(LHS)抽取ND个初始训练样本集SD。

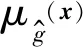
(5) 判断式(27)的收敛条件是否满足。如果满足，执行步骤(7)；否则，执行步骤(6)。

(6) 根据步骤(4)所得学习函数值选出最佳样本点xnew，计算其对应的结构响应值，并扩充到训练样本集SD中，即SD=SD∪xnew，ND=ND+1，并返回步骤(2)。

(28)

4 算例分析

(29)

算例1由四个失效模式组成的串联系统

考虑一个二维输入变量条件下的串联系统，其极限状态函数为[13]

(30)

式中x1和x2为相互独立的标准正态随机变量。

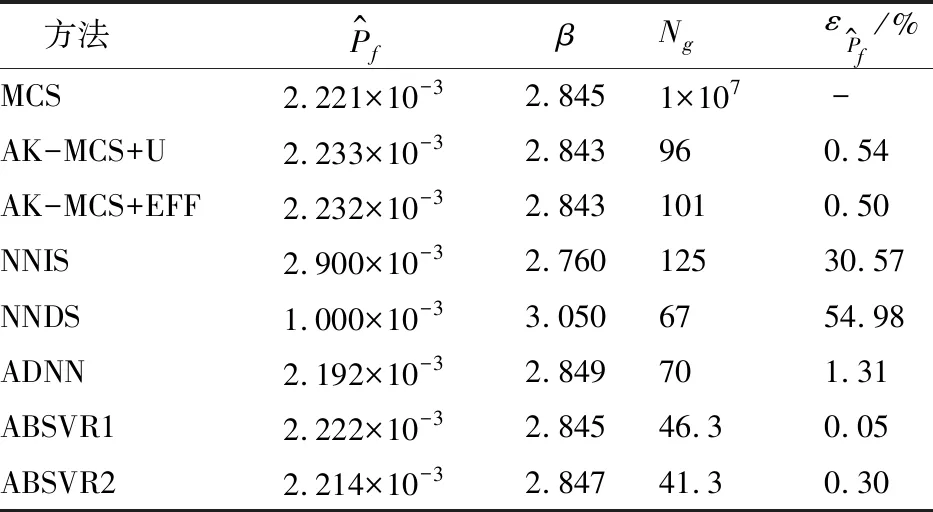
表1 算例1可靠度分析结果对比

为更好地展现ABSVR算法的优异性能，图1给出了ABSVR1和ABSVR2的收敛模型及相应的训练样本点。可以看出，虽然初始训练样本点分布于整个样本空间，但是通过学习函数U和学习函数NLF选取的新样本点绝大多数位于失效边界附近，因此ABSVR1模型和ABSVR2模型能够在重要区域对原极限状态曲面表现出很高的拟合精度。由于考虑了距离测度，相比于学习函数U，本文所提学习函数NLF选取的样本点均匀性更好。此外，由于四个角点区域的概率密度函数值很小，对失效概率估计的贡献基本可忽略不计，所以该部分的拟合精度对最终的计算精度无显著影响。

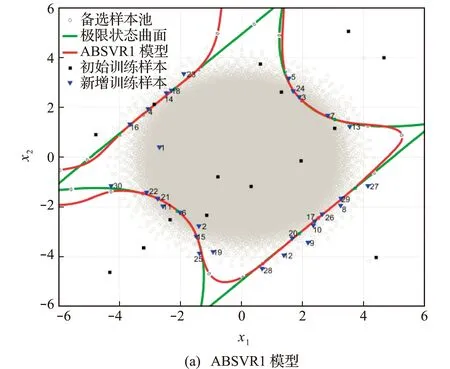
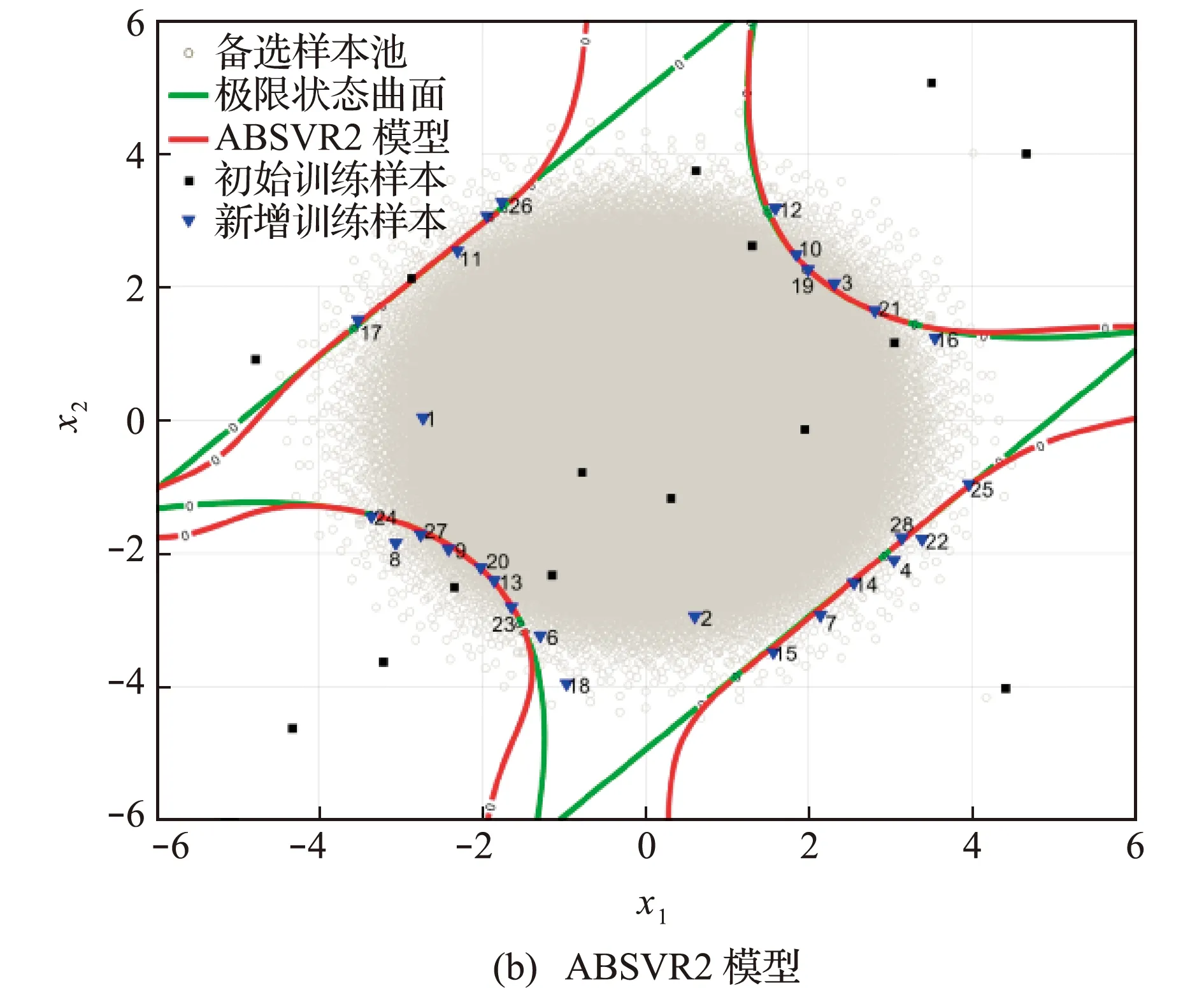
图1 收敛后的Bayesian SVR模型及其训练样本

算例2非线性弹簧振子模型

考虑如图2所示的非线性弹簧振子模型，其极限状态函数为[13]

(31)

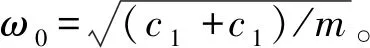
图2 非线性弹簧振子模型

表2 算例2基本随机变量分布参数

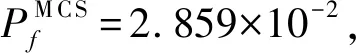
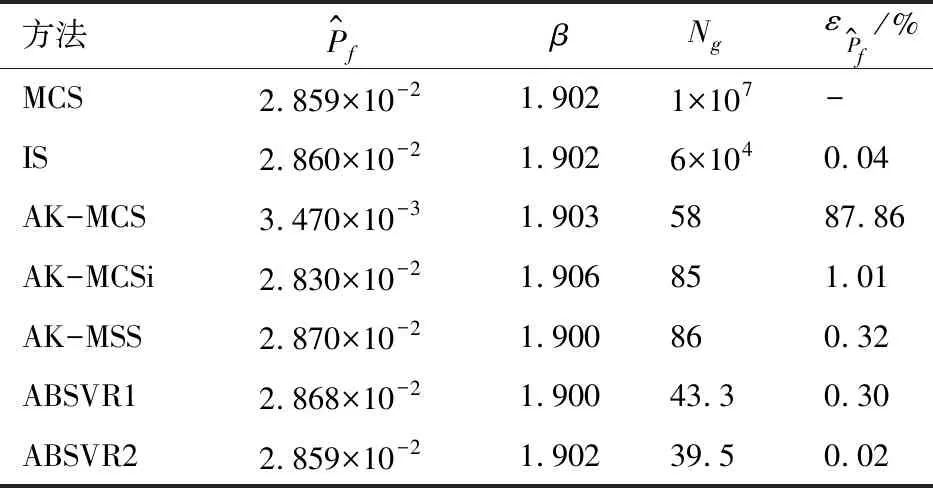
表3 算例2可靠度分析结果对比

图3给出了ABSVR1算法和ABSVR2算法5次独立运算的收敛过程。可以看出，虽然各次运算在前几次迭代过程中有比较大的波动，但在第10次迭代后便能从不同程度迅速逼近精确解，说明了本文方法的精确性、高效性和良好的鲁棒性。

算例3悬臂管结构

考虑如图4所示的悬臂管结构，该结构受3个外荷载及1个扭矩的作用。当结构的屈服强度σ小于最大von Mises应力σmax时,认为结构失效。因此，该结构对应的极限状态函数可表示为[15]

图3 ABSVR1算法和ABSVR2算法5次独立运算的收敛过程

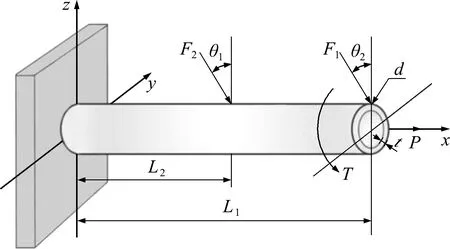
图4 悬臂管结构

g(x)=σ-σmax

(32)

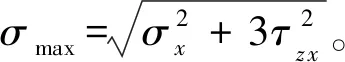
(33)

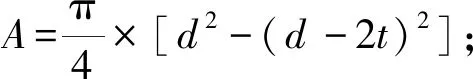
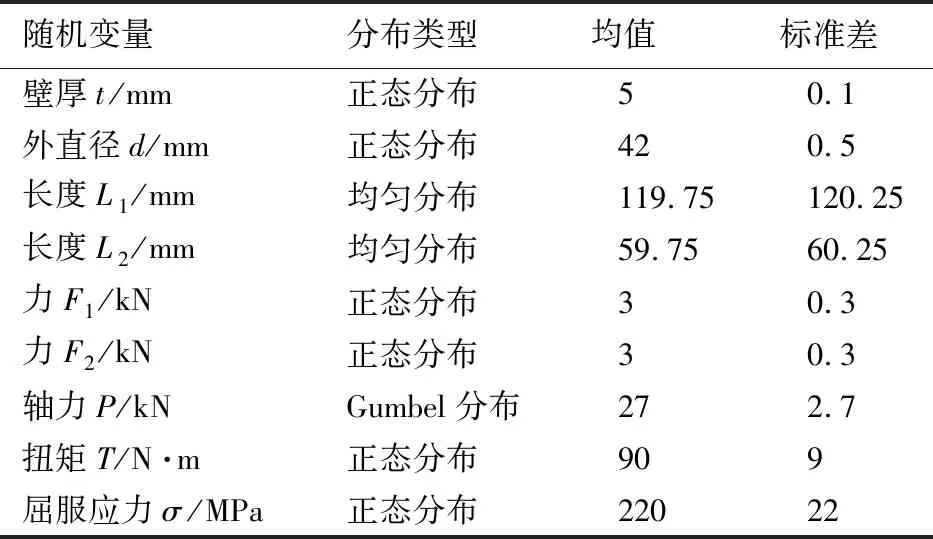
表4 算例3基本随机变量分布参数

表5给出了本文所提算法与其他方法的结果对比，其中参考值由样本量为NT=1×106的MCS经10次重复计算的均值得到，而FORM,SORM,IS、SS以及AK-MCS的结果则是通过默认参数设置的UQLab[30]计算得到。由表5可知，对于本算例涉及的高维度和非线性问题，一阶可靠度法FORM存在较大的计算误差 (12.12%)。虽然二阶可靠度法SORM能有效提高FORM的计算精度，但其功能函数调用次数显著提升。与MCS方法相比，基于方差缩减技术的抽样方法(IS和SS)能在保持一定精度的情况下减少大量的函数调用，但其计算效率仍然很低。相较而言，基于自适应代理模型技术的方法(AK-MCS,ABSVR1和ABSVR2)在计算效率和计算精度上都保持着明显的优势。得益于高效学习函数、有效抽样域策略以及合适收敛条件的综合利用，本文所提的两种方法在整体性能上均优于传统的AK-MCS，能在更少功能函数调用的情况下得到精度更高的失效概率估计。

表5 算例3可靠度分析结果对比

图5给出了ABSVR1算法和ABSVR2算法5次独立运算的收敛过程。可以看出，虽然各次运算在前几次迭代过程中有比较大的波动，但在第6次迭代后便能从不同程度迅速逼近精确解，说明了本文方法的精确性、高效性和良好的鲁棒性。

图5 ABSVR1算法和ABSVR2算法5次独立运算的收敛过程

5 结 论

本文基于Bayesian SVR模型建立了可靠度分析的高效自适应算法(ABSVR)，该算法综合利用了SVR模型在处理小样本、高维度和非线性等问题时表现出的优异性能和贝叶斯推理框架下的概率估计，为进一步提升该类算法的有效性和适用性奠定了基础。此外，本文还从三个方面提升ABSVR的整体性能，一是为有效地引导算法在学习过程中选取位于极限状态曲面附近且对失效概率贡献大的样本点，提出了一种可综合考虑样本点预测值、预测方差、概率密度函数值以及与已有样本点间距等因素的学习函数；二是考虑到失效概率估计的特点，提出了一种新的有效抽样域策略以提高算法的学习效率；三是为防止欠学习或过学习对算法性能产生不利影响，引入一种基于相对误差估计的停止条件，能有效地保证算法在达到给定误差阈值的情况下自动停止。通过三个算例分析得出以下结论。

(1) 本文的算法框架综合利用了贝叶斯支持向量机提供的概率估计信息、有效抽样策略以及合理的收敛准则，通过与学习函数U(即ABSVR1算法)或提出的新学习函数NLF(即ABSVR2算法)结合能很好地适用于结构可靠度分析。相较于其他算法，本文提出的两种方法能更好地平衡计算精度和效率。

(2) 通过学习函数U和学习函数NLF选取的新样本点绝大多数位于失效边界附近，基于此得到的ABSVR1模型和ABSVR2模型均能在重要区域对原极限状态曲面进行高精度的拟合。其中，由于学习函数NLF考虑了样本间的距离测度，所选取的样本点(相比于学习函数U)均匀性更好，因而ABSVR2算法在达到相同精度水平时所需要的功能函数调用次数一般较ABSVR1更少。

(3) 由于概率密度函数值很小的区域对失效概率估计的贡献基本可忽略不计，该部分的拟合效果对最终的计算精度无显著影响，因而在结构可靠度分析中可通过合理的抽样区域策略予以过滤，在不损失精度的情况下可进一步提高计算效率。

(4) 本文方法在学习过程中不涉及复杂的优化算法或非正态变量的等概率变换，简单易懂，有利于进一步推广自适应算法在实际工程中的应用；但所提方法对涉及复杂有限元模型的可靠度分析问题的适用性还需结合算例进一步验证。