碟式离心机层流边界层方程的对称性和不变解

郑明亮

(无锡太湖学院 机电学院，无锡 214064)

1 引 言

碟式离心机作为一种常见分离设备，由于其分离性能好、结构简单和操作方便等优点，已经在化工、冶金、石油和食品等诸多工业领域获得了广泛的应用[1]。碟式离心机内的薄层流动结构不仅与颗粒分离轨迹和分离效率等密切相关，而且直接影响到该单元操作的能量耗损和结构优化[2]。这其中碟片间薄层流动边界层的存在，会产生摩擦阻力，对流体分离与漩涡产生重要影响，因此，研究边界层的流场分布特性，对碟式离心机的碟片结构参数设计有重要意义。

长期以来，碟式离心机薄层流动边界层流场的特性与控制是分离过程科学中的基础问题，主要分为理论数理模型和实验黑箱模型。一般实验方法费用高，周期长；而理论数理模型能有效逼近真实现象，具有预测效果，故得到科研工作者广泛采用。从数学上看，多相流流动模型都是通过非线性流体力学方程组来表达的，所以计算流体边界层方程的显式近似解或精确解析解是流体流动分析和分离控制的首要任务。同时，一般化的N-S方程组的精确解析解是世界级科学难题，若能够首先对一些简化的N-S方程组如层流边界层方程给出有用的解析计算结果，将会大大促进流体动力学基本理论的发展。目前，国内外相关学者在碟式离心机薄层流动分布特征数值计算方面(计算流体动力学软件Fluent仿真和差分格式算法模拟等)集中做了大量工作[3-10]。然而现有计算方法都忽略从方程本身特点出发，缺乏广泛的解析理论推导，从而造成结果有一定误差，也无法进行流场分布的连续性定量显示和灵敏度分析。微分方程的李群分析方法[11,12]源于学者索菲思·李，主要是利用微分方程在群变换下的不变性特性，给出方程的分类、约化、守恒律、降阶甚至积分型解等。该方法对于求解各类常微分方程组和偏微分方程组都是统一适用的，且无论方程是线性或非线性、常系数或变系数，其算法的主要步骤都是固定一样的，因此其极易大规模编程化。可以说，李群分析方法是现今研究微分方程解析解最有效方法之一。然而，国内外还未有关于利用李群分析方法解析计算碟式离心机边界层流场动力学的研究成果，本文针对碟式离心机碟片间隙层流边界层，建立斜板式二维边界层方程，通过李群变换和Lie对称性分析，得到系统偏微分方程的多组生成元和不变解，并对解的有关性质进行了探讨，成功给出边界层速度和厚度的解析表达式和影响因素分析，理论计算完全符合流场实际分布特征。

2 碟式离心机层流边界层方程

碟式离心机的结构[13]如图1所示，混合液经加速后由进液道流入转鼓，由碟片中性孔流入碟片间隙，高速旋转的分离腔带动物料做高速离心旋转运动。碟式离心机转鼓内是一个复杂流动，其流场主要包括速度场和压力场，流体流速是反映转鼓流场的主要特征。

图1 碟式离心机结构

当流体的流动路程较短时，碟片空间的流体不一定能保持层流状态，如图2所示，边界层由二层组成，紧靠壁面很薄的流体层几乎以层流状态流动，故称为层流边界层(层流薄膜)，在层流层上面的液流称为湍流边界层。层流边界层对于已沉降在碟片下表面上的颗粒具有重要影响。

图2 碟片空间边界层

本文讨论的碟片空间与平行板流动仅相差一斜置倾角θ，其中细小颗粒的重力场相对旋转形成的离心场，量级较小，为了简化平面流动的N-S方程，本文忽略重力和科氏力项。按照平板边界层理论[14]，二维定常不可压缩层流边界层方程组的形式为

∂P/∂y=0 位势流动匀速

∂u/∂x+∂v/∂y=0 连续性

(1)

式中f1=Rω2sinθ为流体的离心惯性力沿程分量，ω为离心主轴转速，ρ为流体密度，(u,v)为速度场，P(x,y,t)为压力场，γ为流体动力黏度。与定常的Prandt1边界层微分方程组相比，方程(1)多了离心力位的作用。

3 边界层方程的李对称性

令矢量式的自变量为x=(x,y)，矢量式的因变量为u=(u,v,P),偏微分导算子D为

(2)

引进单参数的李群变换群，

(3)

根据李群的延拓理论，变换式(3)的生成元以及一阶和二阶延拓向量场为

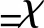
(i,j,i1,i2=1,2;r,q,h=1,2,3) (4)

式中ζ(i)为扩展的i阶无限小生成元函数。

按照微分方程的Lie对称理论，方程(1)在变换式(3)下的不变性为

(5)

求解这些二阶偏微分确定方程组(5)，有如下两组系数函数的表达式为

(6)

式(6)即为边界层方程允许的Lie对称性生成元，可构成相应李代数结构，其中ci为任意常数。

4 边界层方程的不变解

第3节已经得到碟片空间层流边界层方程(1)的允许Lie点变换群(6)，现主要讨论式(6)中一个特殊形式的Lie对称群变换的不变解，即特征方程为

(7)

u=Φ1(λ),v=Φ2(λ)/y,P=Φ3(λ)

(8)

将方程(8)代入式(1)得

(9)

则方程(9)有不变解为

Φ1=6γλ+f1/(6γ),Φ2=0,Φ3=C

(10)

式(10)即为边界层方程的不变解，有这个不变解，本文可从方程的旧解得到新解。

5 结果分析

设某碟式离心机碟片的主要尺寸为R0=107 mm，R1=79 mm，碟片高为70 mm，碟片间隙为1 mm，入口流速度为 0.32 m/s，碟片转速为ωrad/s，液相选择清水，其密度和粘性系数可查表，现定义无量纲速度Ψ和速度比例参数ξ为

Ψ=u/R1ωsinθ,ξ=-0.32/R1ωsinθ

(11)

将Lie对称求解结果(10)和式(8)代入式(11)，得到无量纲速度分布为

(12)

式中τ=y/x为无量纲坐标比，(x,y)为无量纲的碟片平面位置坐标。

边界层厚度在实际问题中具有重要的应用，其直接关系到碟式离心机的生产能力。张乾生[16]指出碟式离心机边界层厚度的近似公式为

(13)

将Lie对称求解结果式(8,10)代入式(13)，则进一步得到边界层厚度为

(14)

本文分别对无量纲速度分布与其影响因素(无量纲坐标比和速度比例参数)的关系，以及边界层厚度与其影响因素(坐标幂律指数和速度比例参数)的关系作拟合曲线。图3反映了不同转速下无量纲边界层速度的分布。可以看出，对于同一种流体，无量纲速度Ψ是碟片速度比例参数ξ的减函数，即边界层内的速度随碟片逆流方向运动速度的增大而减少。图4为不同转速比下边界层厚度σ随x1/2的变化曲线。可以看出，无论碟式离心机转速升高或减少，边界层厚度σ随x1/2的变化是近似线性的。综上所述，Lie对称理论分析与实际现象基本吻合，都很好地验证了Lie对称性方法求解流体边界层流场的有效性。

图3 无量纲速度与y /x的关系

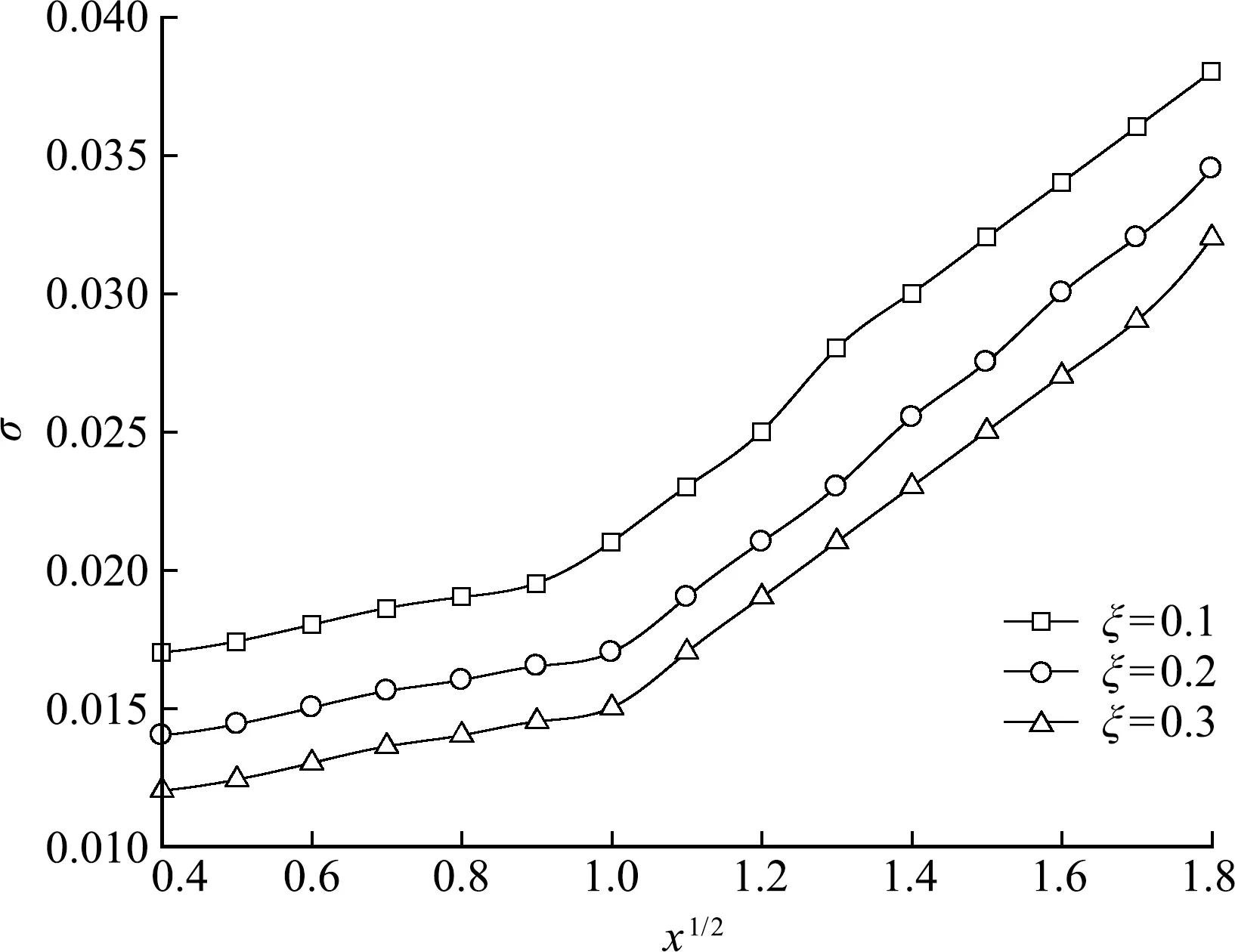
图4 边界层厚度与x1/2的关系

6 结 论

李群分析方法是一类从动力学方程本身出发的解析算法，充分利用了动力学系统内含代数学的群属性以及几何分析的可微属性，是求解非线性微分方程(组)通解的高效算法。该算法的难点就是Lie对称无限小生成元的快速获取。本文运用经典李群分析法求出了碟式离心机斜窄流层流二维边界层方程组的不变性，得到了系统的2组Lie对称生成元和1组不变解，并将这个不变解用到边界层速度和厚度特性分析中。可以看出，斜窄流层流边界层方程和李对性解法可以从流体动力学角度解释离心机料液速度分布和边界层厚度的变化规律。主要结论有,(1) 碟式离心机碟片间隙层流边界层问题存在不变相似解，边界层厚度σ与坐标幂指数x1/2几乎成正比关系；(2) 通过量级分析，无量纲的水平速度Ψ是转鼓速度比例参数ξ的减函数，即边界层内的速度随转鼓逆来流运动速度的增大而减小。本文方法可进一步推广到各类离心机含有固体颗粒的多相流场流动模拟中。