考虑损伤效应的悬索非线性共振响应分析

郑攀攀， 赵珧冰，吴先强

(华侨大学 土木工程学院,厦门 361021)

1 引 言

索结构因其轻质、高强和造型优美等优点，近年来在大跨度空间结构、航空航天领域和海洋工程中应用极其普遍[1]。但由于索结构所处的自然环境较为复杂，在风、雨、温度和外荷载等多因素作用下，不可避免地会出现结构受损，属于典型的易损结构[2]。然而早期损伤具有较大隐蔽性，常规损伤检测难以准确识别，加上温度变化等外界因素影响，导致损伤识别难度更大[3]。事实上，部分索结构在其施工、运营和维护阶段处于一定程度的损伤状态，从而导致其振动特性发生改变。因此，全面描述索结构在损伤后的动力学行为虽难度较大，但无论是对于理论分析还是工程实践，均有重大意义。

近年来，研究人员从理论研究和工程实践等方面对损伤后的索结构开展了相关研究。Lepidi等[4]通过引入损伤程度、范围和位置三个基本参数来系统描述悬索损伤效应，建立了损伤悬索静力学模型。Bouaanani[5]则采用有限差分法探究了损伤位置和损伤范围对悬索模态的影响。Zhu等[6]基于数值方法，分析了损伤对索梁结构动力学性能的影响，发现斜拉索损伤会引起索梁系统动态特性显著变化。Sun等[7]对钢丝腐蚀分布模型、腐蚀速率和腐蚀拉索力学模型进行了研究。研究表明，随着腐蚀时间的增加，拉索的张力垂度和固有频率将出现明显变化。王立彬等[8]通过推导拉索损伤后的索力和线形公式来分析损伤拉索的等效弹性模量。兰成明等[9]对已经服役18年的拉索平行钢丝进行承载力评定，发现拉索腐蚀钢丝屈服强度和极限应变都有所降低，但对于弹性模量而言，腐蚀钢丝与未腐蚀钢丝基本相同。Xu等[10]建立了受损钢丝索力学模型和平面内自由振动的控制方程。研究表明，拉索断丝对短索的静态特性有显著影响，同时拉索断丝数量增加，其固有频率随之降低。Liu等[11]通过实验研究了桥梁钢丝索在腐蚀、微动和疲劳耦合作用下的行为，发现微动疲劳会促进腐蚀介质和钢丝之间的接触，使得钢丝表面的裂纹扩展，钢丝失效，导致钢丝索寿命降低。

上述研究大多集中于损伤后索的静力学特性、材料特性、频率和模态等方面。此外，对于裂纹梁[12]、索网[13]、粘弹性薄板和开孔浅球壳[14]等结构，众多学者对其损伤后的振动特性亦开展了系统研究。然而对于索这类典型的非线性系统而言，已有研究表明，温度变化等因素导致其参数的微小变化可能引发系统共振响应特性的显著改变[15,16]，而从非线性动力学的角度分析损伤对索共振响应特性的影响则鲜有报道。因此，本文引入损伤程度、范围和位置三个参数，利用Hamilton变分原理，推导了损伤悬索的非线性运动微分方程，基于Galerkin法[17]，建立损伤悬索离散后无穷维动力学方程。以主共振为例，采用高阶多尺度法求解其共振响应近似解及幅频响应方程。最后通过数值算例探究损伤效应对不同垂跨比悬索非线性主共振响应的影响。

2 损伤悬索的动力学建模

假定悬索由均匀连续的弹性材料构成，且只考虑索横截面上均匀分布的拉应力和拉应变，忽略剪切刚度和抗弯刚度。损伤悬索无应力状态下的构形如图1所示，采用弧坐标s贯穿悬索全长，EA表示轴向刚度，EAd(s)为悬索的残余轴向刚度。其中Ad(s)为悬索锈蚀后的残余截面面积，通过借鉴锈蚀钢筋测量截面面积的方法可以得到[18]。本文为了研究方便，假设锈蚀部分的悬索残余截面面积相等。悬索损伤区域为[a1,a2]，L0为悬索无应力状态下的索长。

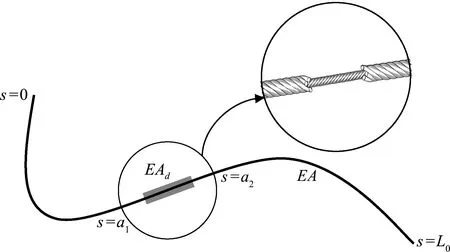
图1 损伤悬索无应力状态下的构形

引入以下三个无量纲参数来定义悬索的损伤程度、范围和位置[4],

(1)

悬索损伤程度在整个索长上的变化用分段函数(2)表示,

(2)

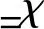
(3)

式中Hd(H)和bd(b)分别为损伤(无损伤)悬索的初始水平张力和垂度，通过求解其静力学平衡方程可以得到。

2.1 运动微分方程

(4)

(5)

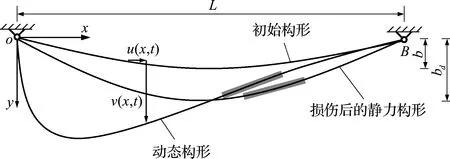
图2 悬索构形及其特性

该非线性系统的边界条件和连续条件为

(6)

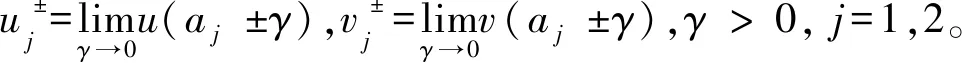
由索轴向张力平衡可得

(7)

式中ε1和ε2为悬索的拉格朗日应变。

基于拟静态拉伸假设，并结合方程(7)得到损伤悬索轴向应变的拟静态解，即

ε(x,t)=e(t)/[1-ζ(x)]

(8)

式中e(t)是一个只与时间t相关的量。

对式(8)从0～L积分并引入边界条件(6)可得

(9)

因此，损伤悬索面内运动方程可以简化为

(10)

引入以下无量纲参数

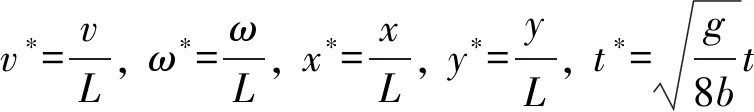
(11)

因此，式(10)可变换为

(12)

2.2 Galerkin离散

采用Galerkin法对式(12)进行无穷维离散，面内运动的位移函数可表示为

(13)

(14)

式中

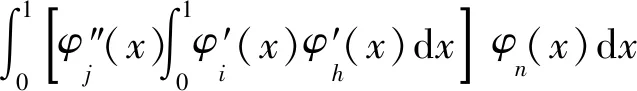
3 摄动分析

摄动分析是采用摄动方法求得方程的近似解，通过引入一个小参数作为摄动量，然后假设解可以按照小参数的幂级展开。本文采用摄动法的高阶多尺度法(小参数的幂级为4)来求解悬索单模态非线性主共振响应的近似解，引入新的独立时间变量Tn=εmt(m=0,1,2,3,4)，可知

(15)

式中ε为无量纲小参数。

外激励频率和固有频率通过引入调谐参数表示

Ω=ωn+ε2σn 1+ε4σn 2

(16)

式中ωn为固有频率，σn 1和σn 2为两个调谐参数，总的调谐参数可表示为

σn=σn 1+σn 2

(17)

采用高阶多尺度法[15]求解方程(14)，可得

(18)

(19)

此时，稳态响应可表示为

(20)

式中an为响应幅值，t为时间，γn为相位，

(21)

4 算例分析

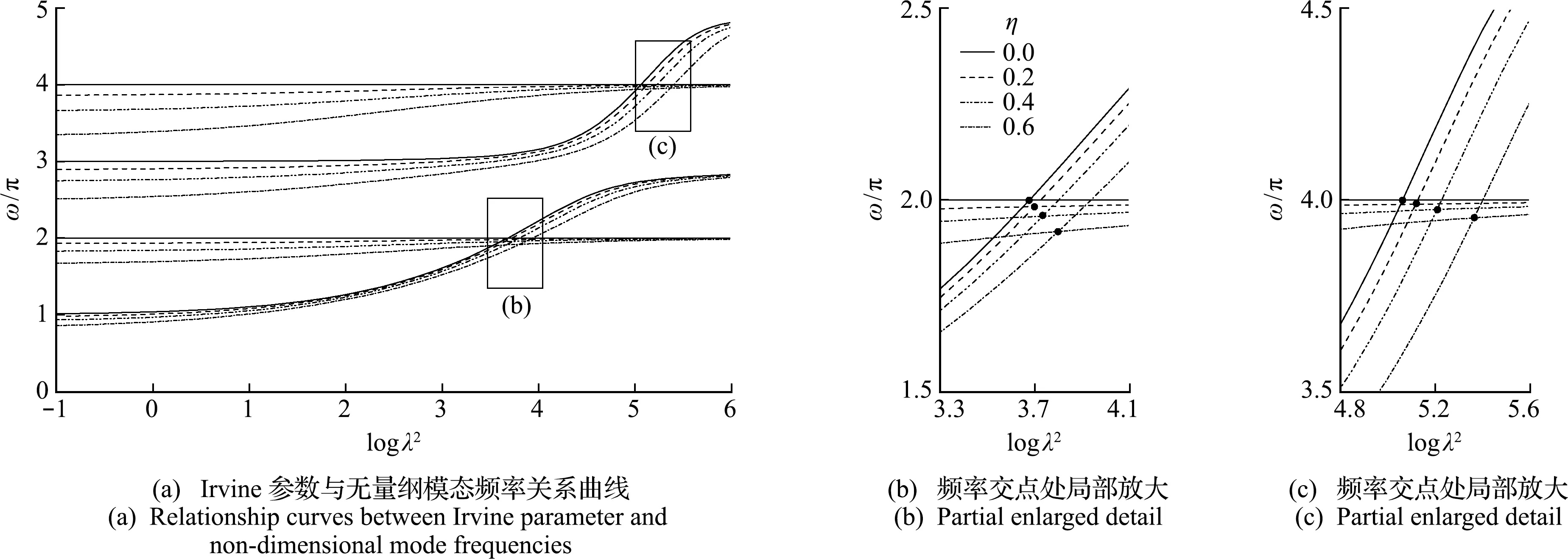
图3 损伤对模态频率的影响

如图4(c,d)所示，当悬索垂跨比为0.015和0.02时，悬索均展现出先软后硬的弹簧特性。且随着损伤程度和范围增大，幅频响应曲线向右偏转程度降低。可以明显看出，垂跨比为0.02时损伤对悬索振动特性的影响大于垂跨比为0.015时。悬索垂跨比继续增大至0.025，如图4(e)所示，此时除未损伤外，悬索均展现出先软后硬的弹簧特性，且随着损伤强度增加以及损伤范围增大，系统多解区域明显增大。尤其是大幅振动区间，系统振幅在损伤影响下呈明显增大的趋势。图4(f)中，悬索垂跨比继续增加至0.03，系统均展现出明显的硬弹簧特性，随着损伤强度和范围增加，幅频响应曲线向右偏转程度降低。倘若垂跨比继续增加，损伤效应对振动特性影响将逐渐下降，且均展现出明显的硬弹簧特性，不再赘述。

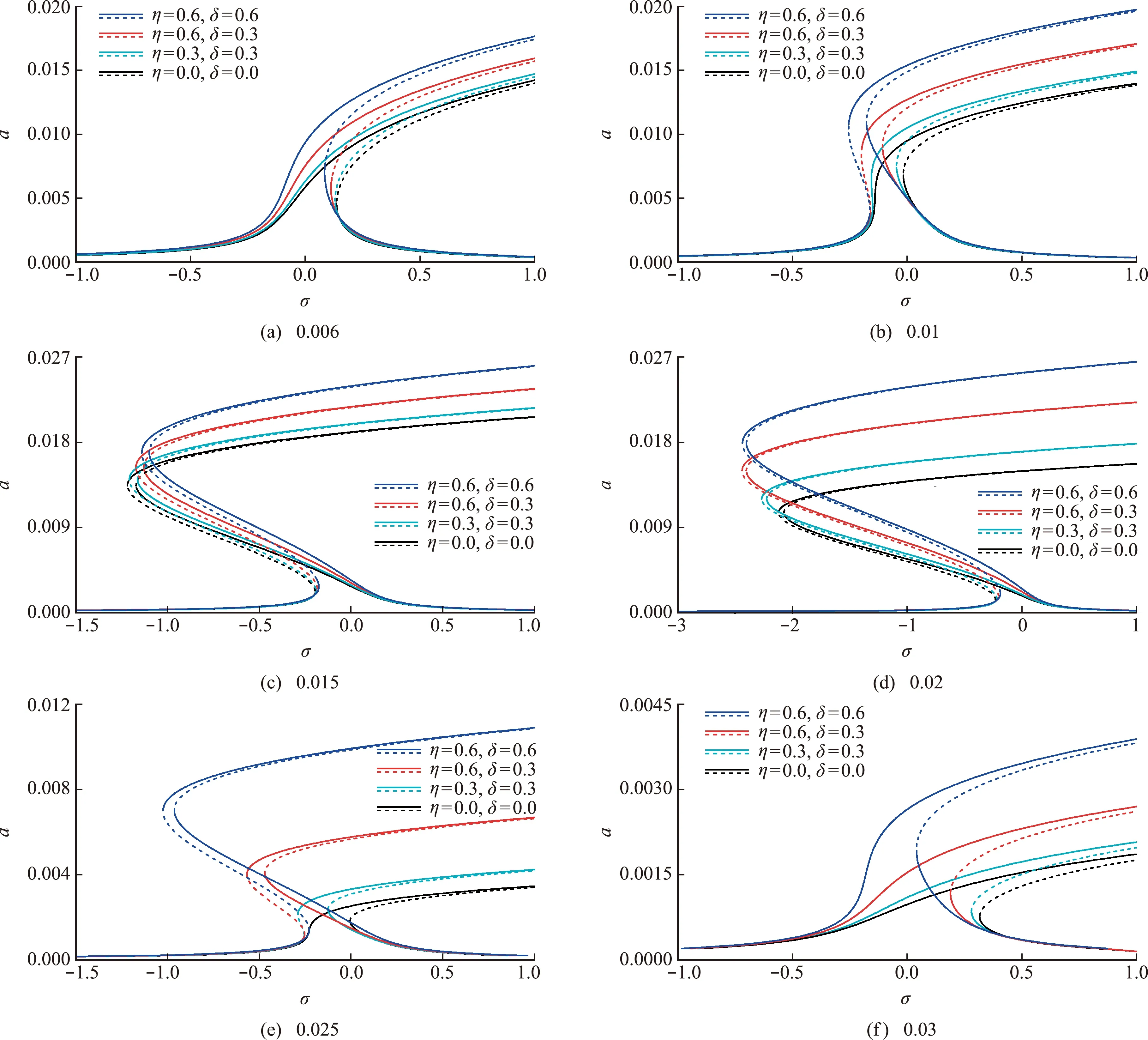
图4 损伤对悬索幅频响应曲线的影响

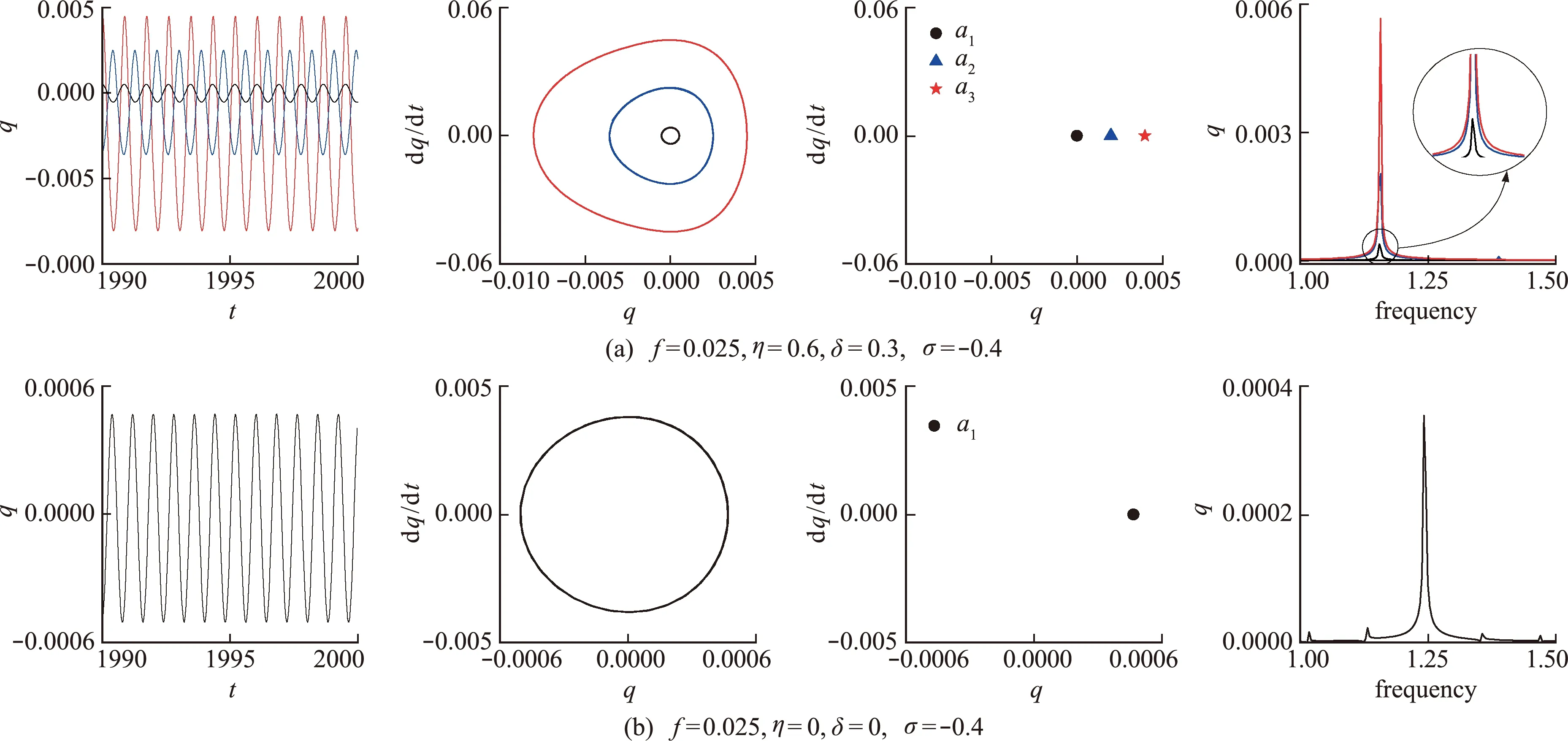
图5 考虑损伤影响的时程曲线、相位图、庞加莱截面以及频率谱

5 结 论

悬索一旦发生损伤，其张力减小，垂跨比增加，将形成新的静力构形。受损悬索的固有频率将随着损伤程度的增加而减小，且不同垂跨比悬索，其正/反对称模态频率受损伤影响程度区别明显。损伤使得正/反对称模态频率交点发生偏移，影响系统内的共振响应特性。当悬索垂跨比较小(如0.006)或者大于某值(如0.03)时，悬索硬弹簧特性将随着损伤程度和范围的增大而减弱。当悬索垂跨比介于两者之间时，系统先软后硬的弹簧特性也与损伤程度和范围密切相关，展现出定量和定性改变。损伤效应甚至会直接改变系统稳态响应幅值以及其解的数量，可能引发系统发生大幅振动，危害结构安全。