探究碰撞速度关系 深化碰撞作用模型——碰撞模型的拓展与应用

湖北 许 文

碰撞是物体间相互作用的一种方式，在相互作用过程中物体的速度、动量、能量等均会发生变化。对于碰撞问题，我们一般会根据动量关系、能量关系、速度关系等进行分析与判断，但在能量关系中往往涉及二次方程(或不等式)，运算过程较复杂。本文根据碰撞过程中物体间相互作用的特点，探究碰撞问题中隐含的速度关系，深化碰撞模型，拓展碰撞问题的分析思路，简化解题过程，提高解题效率。

一、碰撞中两个速度关系

物体的碰撞过程一般要经历两个阶段。第一阶段，两物体从接触开始相互挤压，接触区域因物体间的相互挤压而发生形变，当两物体的速度相等时形变达到最大；第二阶段为形变恢复阶段，可分为三种情况。(1)如果两物体的形变完全恢复后，两物体脱离接触，这种碰撞称为弹性碰撞，整个碰撞过程无机械能损失；(2)如果两物体的形变部分恢复(未完全恢复)后，两物体脱离接触，这种碰撞称为非弹性碰撞，整个碰撞过程有机械能损失，损失的机械能与物体形变恢复的程度有关；(3)如果两物体的形变完全不能恢复，碰撞结束后粘在一起运动，这种碰撞称为完全非弹性碰撞，相较于前两种碰撞，完全非弹性碰撞过程损失的机械能最大。

通常情况下，由于碰撞过程时间极短，且物体间相互作用的内力远大于外力，碰撞全程都遵循动量守恒定律。分析碰撞的相关问题，一般可用以下三个关系。(1)动量关系：动量守恒，即碰撞过程中系统的总动量守恒；(2)能量关系：动能不增，即系统碰撞前的总动能大于或等于碰撞后的总动能；(3)速度关系：速度合理，如碰前两物体同向运动，若要发生碰撞，则有v后者>v前者；若碰后两物体同向运动，有v后者≤v前者。

一般来说，应用以上三个关系式，就能够对碰撞问题进行分析与判断，但能量关系涉及二次方程(或不等式)，其运算过程较复杂且容易出错，因此我们可根据动量与能量关系，探究碰撞中隐含的速度关系，简化问题的分析与计算。

1.碰撞前后相对速度大小不增加

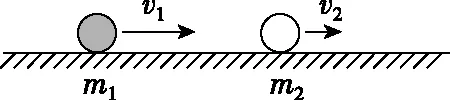
图1

①

由能量关系有

②

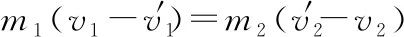
③

由②式得

④

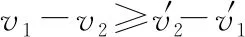
⑤

第⑤式表明，碰撞前后物体的相对速度大小不增加，即碰撞前物体的相对速度大于或等于碰后物体的相对速度(取等号时对应着弹性碰撞)。

【例1】如图2所示，质量为m的A球沿光滑的水平面以速度v0向右运动，与静止的质量为4m的B球发生碰撞，碰后A球以v=av0(待定系数a<1)的速率弹回，并与固定挡板P发生弹性碰撞，若要使A球能与B球能再碰，则a的取值范围为

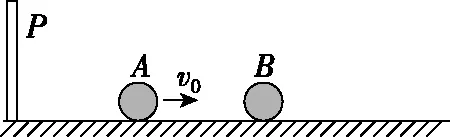
图2

( )

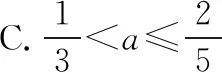
【解析】设碰后B球的速度为vB，选取向右为正方向。

解法1：由动量关系有mv0=-mav0+4mvB

A球与挡板P碰后返回的速度大小为av0，若A球再与B球相碰，则有av0>vB

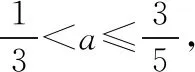
【答案】D

【例2】(原创)如图3所示，质量为m=2 kg、长度为L=0.5 m的木板静止在光滑的水平地面上，木板的两端固定有弹性挡板M、N。一质量为m0=4 kg的小物块(可视为质点)静止在木板的中点，让小物块以v0=6 m/s的速度水平向左运动。已知小物块与木板之间的动摩擦因数μ=0.1，小物块与挡板的碰撞时间很短且没有能量损失，重力加速度g=10 m/s2。求小物块在木板上相对滑动的时间t。

图3

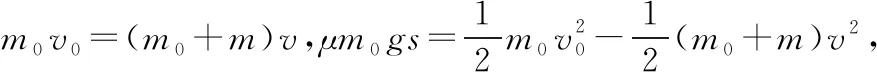
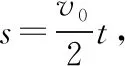
【点评】本题求解小物块相对木板运动的时间，若以地面为参照系，求出小物块每次与挡板碰撞后运动的时间，再求总和，这种解题过程较为繁琐。而上述分析求解中利用了两物体弹性碰撞前后相对速度大小不变，选取木板为参照系，小物块相对木板的运动等效为一个匀减速直线运动，求解过程较简洁明了。

2.弹性碰撞速度变化对称

由动量守恒定律有

由能量守恒定律有

两式联立解得

一般情况下，两物体弹性碰撞后的速度可由上述二元二次方程组解出，但数学运算过程较复杂，其结果的表达式也难以记住，使学生将大量时间用在求解此类问题的数学运算上，导致解题效率不高。

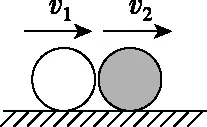
(a)

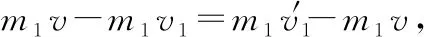
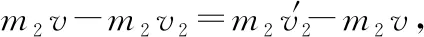
又由m1v1+m2v2=(m1+m2)v可知，只要求出形变最大时(即发生完全非弹性碰撞时)的速度v，由以上两式即可得出弹性碰撞后的速度，从而简化计算过程。

【例3】(多选)质量分别为mA=1 kg、mB=2 kg的两个小球A、B在光滑水平面上沿同一直线，同一方向运动，B球在前，A球在后，它们的速度分别为vA=6 m/s，vB=3 m/s。当A球与B球发生碰撞后，A、B两球的速度可能为

( )

A.vA=4 m/s，vB=4 m/s

B.vA=2 m/s，vB=5 m/s

C.vA=-4 m/s，vB=6 m/s

D.vA=7 m/s，vB=2.5 m/s

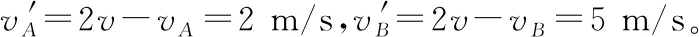
【答案】AB

二、碰撞模型的拓展

碰撞过程中物体间发生相互作用，相互作用的物体可以接触，也可以不接触；碰撞中物体间相互作用过程可能很短暂，也可能持续一段时间。下表中列举了几种两物体间的相互作用过程，这些作用过程均可等效为两物体的碰撞过程。

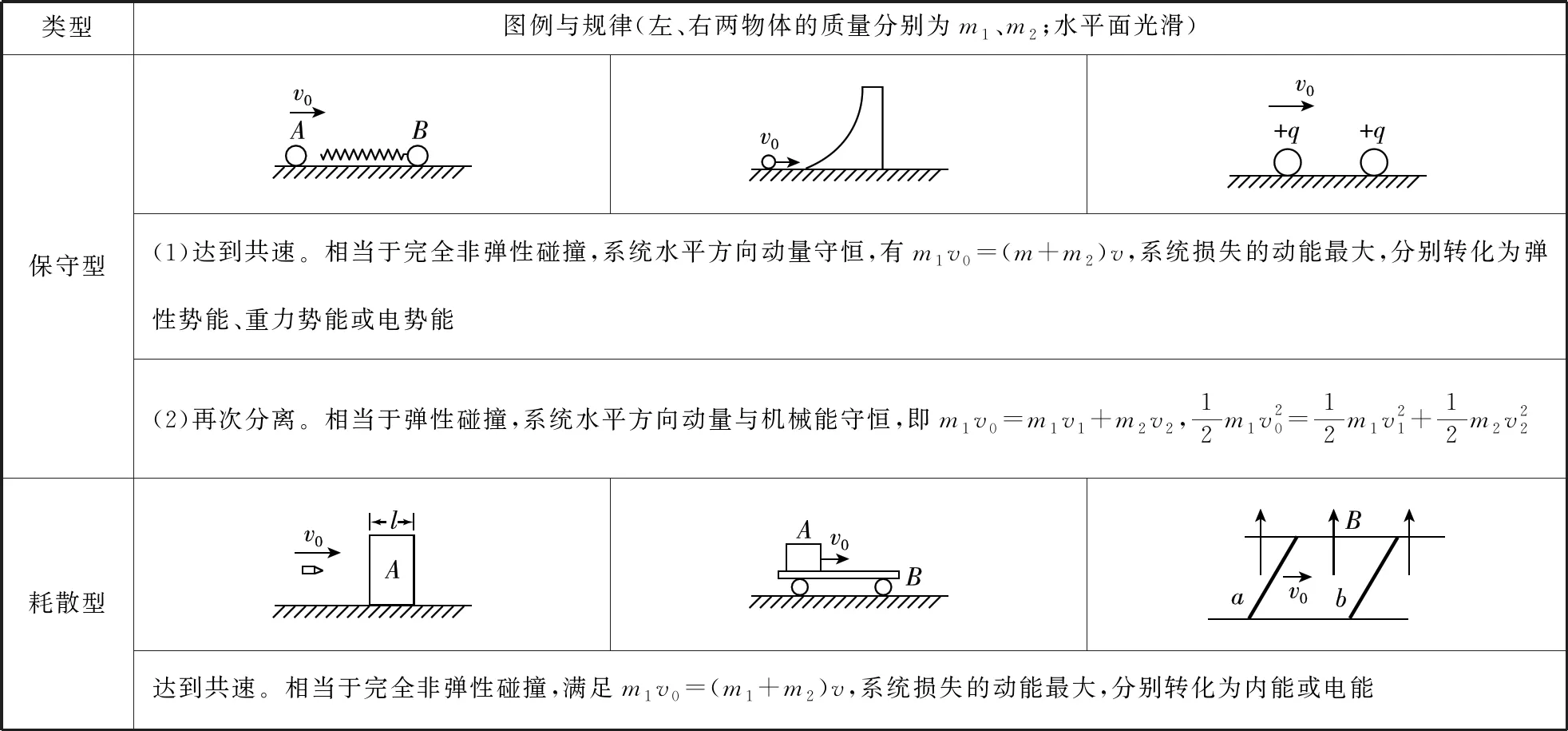
类型图例与规律(左、右两物体的质量分别为m1、m2;水平面光滑)保守型(1)达到共速。相当于完全非弹性碰撞,系统水平方向动量守恒,有m1v0=(m+m2)v,系统损失的动能最大,分别转化为弹性势能、重力势能或电势能(2)再次分离。相当于弹性碰撞,系统水平方向动量与机械能守恒,即m1v0=m1v1+m2v2,12m1v20=12m1v21+12m2v22耗散型达到共速。相当于完全非弹性碰撞,满足m1v0=(m1+m2)v,系统损失的动能最大,分别转化为内能或电能

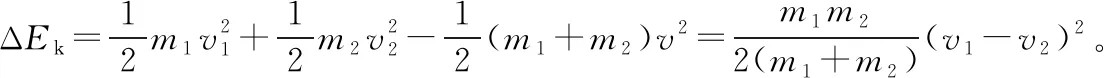
【例4】(多选)如图5所示，质量为M的四分之一光滑圆槽B静置于光滑水平地面上，槽底端与水平面相切，一质量为m的小球A从水平地面以初速度v0滑向圆槽，从底端沿槽上滑，未冲出圆槽，最后滑回水平地面。已知重力加速度为g。下列说法中正确的是

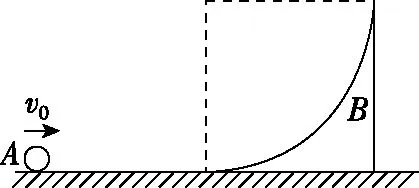
图5

( )

C.小球上滑过程比下滑过程的动量变化大

D.小球上滑过程圆槽的动能增加量是下滑过程圆槽的动能增加量的3倍

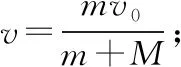
【答案】AD

【例5】如图6所示，光滑悬空轨道上静止一质量为3m的小车A，用一段不可伸长的轻质细绳悬挂一质量为2m的木块B。一质量为m的子弹以水平速度v0射入木块(时间极短)，在以后的运动过程中，细绳离开竖直方向的最大角度小于90°，不计空气阻力，已知重力加速度为g。求：

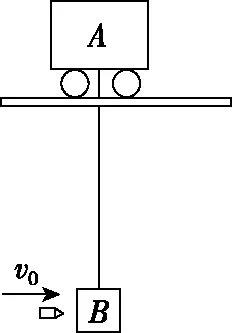
图6

(1)木块B能摆起的最大高度；

(2)小车A在运动过程中的最大速度大小vA。

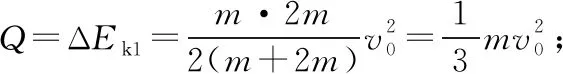
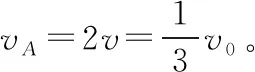
【点评】子弹射入木块的过程是一个完全非弹性碰撞过程，此过程中系统的动量守恒，损失的动能转化为内能；此后木块(含子弹)与小车通过细绳发生相互作用，木块(含子弹)从最低点向右摆到最高点的过程等效木块(含子弹)与小车组成的系统发生完全非弹性碰撞，损失的动能转化为木块(含子弹)的重力势能；当子弹射入木块后，木块(含子弹)最低点摆到最高点后，又从最高点再次摆回到最低点的过程可等效为弹性碰撞过程，由弹性碰撞的相关结论，可快速得到解题结果。

碰撞过程往往会涉及动量与能量的综合分析，涉及碰撞后物体速度的计算。本文通过对碰撞过程与特点的分析，揭示出碰撞过程中两个隐含的速度关系，优化解题的计算过程；拓展碰撞模型，为分析此类相互作用问题建立合理的物理模型，提学生高知识的迁移与应用能力。