粗糙元对微通道稀薄气体流动换热影响研究

许 啸，沈 妍，姚寿广, 谷家扬，刘 锐

(1.江苏科技大学 机电与动力工程学院，张家港 215600)(2.江苏科技大学 能源与动力学院, 镇江 212100)(3.江苏科技大学 海洋装备研究院，镇江 212003)

近年来，随着微机电系统技术的迅猛发展，微尺度流动与换热问题成为了科技前沿领域的研究热点.微尺度流动是一种运动尺度远小于宏观流场的流动现象，其空间尺度通常在毫米级以下，达到微米量级[1].在这种情况下，不但流体运动会呈现出壁面速度滑移、稀薄效应、边界层/主流相互干扰等与宏观流体迥异的特殊现象，其传热性能也出现了热蠕动、粘性加热等特殊效应[2]，同时由于宏观连续性假设在微观尺度下逐渐失效，传统的计算流体力学理论和数值方法也开始出现难以适用的问题，这表明了微尺度流动与换热从理论到现象均具有极大的特殊性，亟待深入探索.据此，众多学者对该类问题进行了研究，并在各方面获得了相应的成果[3-7].

在微尺度流动与换热的研究中，壁面粗糙元对其特性的影响是一类重要的研究方向.由于流动和换热的空间尺度趋于微型，固壁表面粗糙元的细微变化对流动换热的影响被放大，宏观条件下相对粗糙度不超过5%则其对摩擦因数的影响可忽略这一结论已然不再适用[8]，文献[9]实验研究表明，当直径620 μm的微管道相对粗糙度增加至0.355%时，该管道的摩阻系数有明显变化；文献[10]通过实验观测到特征尺度为50～254 μm的硅或不锈钢微管中，相对粗糙度的范围为0.7%～3.5%时，泊肃叶数大约增加10%～20%.而另一方面，表面粗糙度的增加将提升流体与固体相互接触的表面积，由于微尺度流动具有较大的面容比，这种改变将明显提高其换热性能，文献[11]在壁面上设置不同形状的粗糙元，并采用数值模拟的方法进行分析研究，结果显示随着粗糙元高度的增加，流体传热效果显著增强；文献[12]以R134a为工质，测试其在3种不同表面粗糙度的微型蒸发器中的流动与换热性能变化，结果表明，随着粗糙度的增加，在低到中等热流流量情况下，两相传热系数增强了45%.由此可见，微尺度流动中表面粗糙元的变化对其流动传热性能的影响是多方面的，为进一步研究该类问题，文献[13]基于热力学第一和第二定律对三角形凹穴加梯形肋片等六种结构的微尺度通道流动进行了模拟研究；文献[14]通过试验研究了具有不同表面粗糙度的不锈钢制微通道的流动和传热特性；文献[15]采用实验和数值模拟相结合的方式，研究了表面粗糙度变化对不同结构微通道内流动传热系数的影响；文献[16]采用数值模拟方法对双电层作用下的幂律流体在正弦粗糙微通道中的流动和传热问题进行了研究；文献[17]采用有限元方法分析了壁面随机粗糙度对流速、压降等流动性能的影响；文献[18]采用直接模拟蒙特卡洛法(direct simulation of Monte Carlo，DSMC)对具有三角形粗糙元表面的微通道内气体流动进行了模拟研究；文献[19]以分形几何学理论为基础，采用数值方法对多尺度自仿射的表面粗糙度进行了模型化表述，并对建立在该模型基础上的微尺度通道流动进行了模拟研究等等.

综上所述，壁面粗糙元对微尺度流动和换热的影响研究具有十分重要的意义，若能够掌握不同状态下粗糙元对微尺度流动和换热的影响关系，则其对各类型高性能微尺度流动和传热装置的设计与优化将有很大帮助.然而，受研究设备和方法的限制，目前的微尺度流动换热研究主要集中在尺度相对较高的连续流态，更低尺度的稀薄流态研究则较少.因此，针对微通道中的稀薄气体流动和换热问题，文中采用数值模拟方法展开研究，首先验证方法的正确性，然后通过改变粗糙元的数量、分布与结构尺寸，研究并分析壁面粗糙元对微通道中稀薄气体流动和换热性能的影响，从而为相应的高性能流动换热装置的设计提供参考.

1 理论基础

1.1 微尺度稀薄气体流动

从微观上看，流体运动可以视为大量分子运动的集合，通常情况下，宏观流动中的分子运动尺度与其整体的流动尺度相比基本可以忽略不计，流动总体上呈现连续性特征.然而，当流体密度或流动空间尺度降低到一定程度时，流体中的分子碰撞间距与空间尺度相比将不再是可忽略的小量，此时流体不再满足连续介质假设条件，其对应的控制方程中的输运系数开始失效，这就意味着传统计算流体力学理论中经典的Navier-Stokes方程无法适用于模拟这一领域的流动问题，转而需要采用基于Boltzmann方程的稀薄气体动力学方法进行模拟[19].

连续流和稀薄流属于不同类型的流动，两者的控制方程有所区别，因此在进行数值模拟研究时，如何对流动类型进行划分是首要问题.目前，学术界通用的方法为Knudsen数法[20]，稀薄流特征参数Kn的表达形式为：

Kn=λ/L

式中：λ为平均分子自由程；L为流动特征长度.钱学森最早采用Kn数将稀薄气体流动分为三大领域：滑流领域、过渡流领域和自由分子流领域，其中Kn数均大于等于0.01；而当Kn数小于0.01时，流动为连续流[19].

从上式来看，平均分子自由程的增大或流动特征长度的减小都将使流动的Kn数增大，即趋向于稀薄，微尺度稀薄流动的成因主要是后者.当流动空间尺度降低至数个微米时，常压条件下空气流动的Kn数也将接近甚至超过阈值0.01，文中主要研究的流动与传热问题即属于这一类型.

1.2 DSMC方法

文中采用直接模拟蒙特卡洛(DSMC)法[21]进行研究，该方法以分子运动模型为基础，采用大量的模拟分子代表真实气体分子，并将模拟分子的位置、速度等信息保存在计算机内；计算时将分子的运动与碰撞相互解耦，即将分子的真实运动划分为位移和碰撞两种过程，分子位移可以直接表述为单位时间内分子在速度方向上的运动，碰撞过程则需要在单元内选取合适的分子对，并采用合理的碰撞模型处理相应的分子信息变化；当流场最终趋于稳定时，采用统计方法得出单元中的宏观信息值.DSMC方法的核心思想是通过直接模拟分子的物理运动来获得流场的宏观统计结果，相比于直接求解Boltzmann方程，不仅更易于引入真实情况下的物理运动模型，而且已被证明收敛于Boltzmann方程[22]，其有效性和可靠性均已得到了充分的验证，因此成为了目前在稀薄气体流动模拟中应用最为广泛的方法.

2 数值方法验证

采用非结构网格DSMC方法对文献[23]中的微管道流动(微尺度泊肃叶流)进行数值模拟.根据文献中的参数，该管道长2 μm，高0.4 μm，结构尺寸和网格如图1.气体种类为氮气，进出口均为压力边界，出口压力为1个标准大气压，入口压力为出口压力的2.5倍；管内气体和壁面温度均为300 K.根据文中的参数，初始状态下其入口和出口处的Kn数分别为0.055和0.123，均大于0.01，因此该算例中的流动为稀薄流，采用DSMC方法进行模拟是合理的.计算中采用约101万模拟分子，共计算40 000时间步，其中计算35 000时间步，统计5 000时间步，单位时间步长为1×10-12s.

图1 微通道的结构尺寸和网格Fig.1 Structure size and grid of the microchannel

图2为微通道流场的计算结果.

图2 微通道流场计算结果Fig.2 Computational results of the microchannel flow field

从图中可以看出，在进出口压差的驱动下，密度与压力呈均匀的段状分布，由于管道平直且没有粗糙元的干扰，各分段的长度基本相同，入口高压来流在管道中的膨胀受两侧壁面的限制，其压力和密度等值线在近入口处的中心线上略向下游方向凸起，而出口中心线上的高速膨胀则导致该位置处的压力和密度等值线向管内略微凹陷；速度变化主要集中于通道的中心线位置，由于中心线上的密度逐渐下降而前后压差基本为均值，该位置处的流体质点呈逐渐加速的状态，导致流场速度在入口处增长缓慢而在出口处变化剧烈，整体分布呈锥形；在管道两侧近壁面处，流体受固壁粘性作用速度较低，但最低值并不为0，与此同时，近壁面流场速度分布沿管道流向存在差异，靠近入口的壁面流速最低，而接近出口的壁面流速已上升至50～60 m/s，速度滑移现象明显；在管道的直径方向上，速度边界分层结构明显，尤其在入口近壁面处，边界层厚度约占总通道高度的50%，对主流产生了不可忽视的影响.由此可见，文中方法的计算结果体现了微通道流动的各类效应，其整体趋势与微尺度压差流动特征相符，初步证明了结果的合理性.

图3为微通道流场内壁面和中心线上的部分特征值分布情况，包括速度分布、Re数分布和中心线压力与出口压力的比值，图中L为通道总长度.从速度和雷诺数的分布图中可以看出，在压差的驱动下，壁面和中心线上的速度均出现了近似线性式的增长，其中入口和出口处的壁面速度约为26 m/s和79 m/s，比率约为1∶3，中心线速度约为80 m/s和166 m/s，比率约为1∶2.1，可见壁面速度增长率更高，主流加速受到了粘性的抑制，这不仅清晰地反映了微通道中壁面速度滑移的发展过程，而且表明了与宏观尺度流动相比，微尺度流动中壁面粘性对流体分子的阻滞作用相对较弱，无法有效的将流体约束在壁面上；另外，主流速度的发展受到了来自边界层粘性的干扰，这表明分子间粘性碰撞的影响在微尺度流动中更加突出.

图3 微通道流场中的特征值Fig.3 Characteristic values of the microchannel flow field

在Re数的计算中，文中将管道高度取为特征长度，氮气的动力粘性系数为1.78×10-5Pa·s，结果显示，通道内流动的Re数最大值约为5，说明微通道流动属于极低Re数流动，其粘性效应对流动的影响占主导；中心线上的Re数约从5.0降至4.75，降幅占总变化范围的5%，而壁面上的Re数除进出口边界点上的值受边界条件影响有波动外，其它值呈线性增长趋势，数值约从1.25升至1.8，升幅约占总变化范围的55%，这进一步表明了微通道壁面粘性效应偏弱，导致来流惯性力对壁面流场的影响逐渐升高，而主流气体受边界层粘性的干扰，惯性力影响略有下降，这些特征均与微尺度流动中的特性相符.图3(c)给出了中心线压力与出口压力的比值，并将该值与文献[24]的计算值进行了比较，可以看出，中心线压力变化接近于线性，表现出明显的层流特征，文中计算值与参考值也符合较好，最大差异不超过总变化幅度的1.6%，由此可以证明文中方法的准确性.

3 粗糙元结构和分布不同时微通道内流动与换热模拟

文中采用DSMC方法对含有粗糙元的微通道内稀薄气体流动和换热过程进行模拟.为方便对照分析，仍采用验证算例中的微通道为基础模型，进出口边界条件中的压力比仍为2.5∶1，但来流温度设为200 K，而壁面温度设为常温300 K，以便分析相应的换热效应；粗糙元设为不同半径的二维半椭圆结构体，其在X和Y方向的半径分别为0.07 μm和0.02 μm，上下壁面对称分布，在模拟中通过改变粗糙元的数量、分布位置以及高度尺寸来分析其对微通道稀薄流动与换热的具体影响.

3.1 粗糙元数量与位置分布

文中研究粗糙元数量和分布位置变化所产生的影响，各模型和网格结构如图4.

图4 不同粗糙元数量和分布的微通道网格结构Fig.4 Grids and structures of the microchannels with different number and distribution of rough elements

图5～7为不同结构微通道流场的速度、温度和压力分布.从结果中可以看出，随着粗糙元数量的增加，流场出口处的速度有所下降，温度则呈上升趋势；另一方面，粗糙元的数量和位置变化并没有对管内流场的结构产生较为明显的影响，固壁表面速度和温度与参考流场中对应位置处的数值基本相同，通道内流场的边界层结构并未发生较大改变；从压力结果来看，粗糙元的存在使管道内对应位置处的等值线簇发生了一定程度的弯曲，并使其向粗糙元中心方向集中.这说明了粗糙元对微通道流动的主要影响是增大流固体接触面积和产生局部压缩效应，从而导致通道内的流动换热性能发生变化，但在该结构尺寸不变的条件下，粗糙元数量和分布的变化不会明显改变原有的速度滑移效应和边界层结构，对流动和换热的整体趋势也不会产生重大的影响.

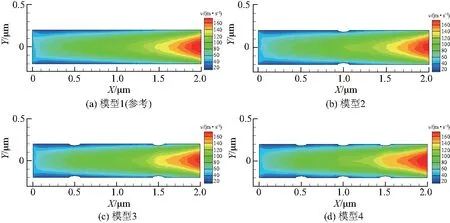
图5 不同结构微通道内流场速度分布Fig.5 Velocity distribution in the microchannels with different structures

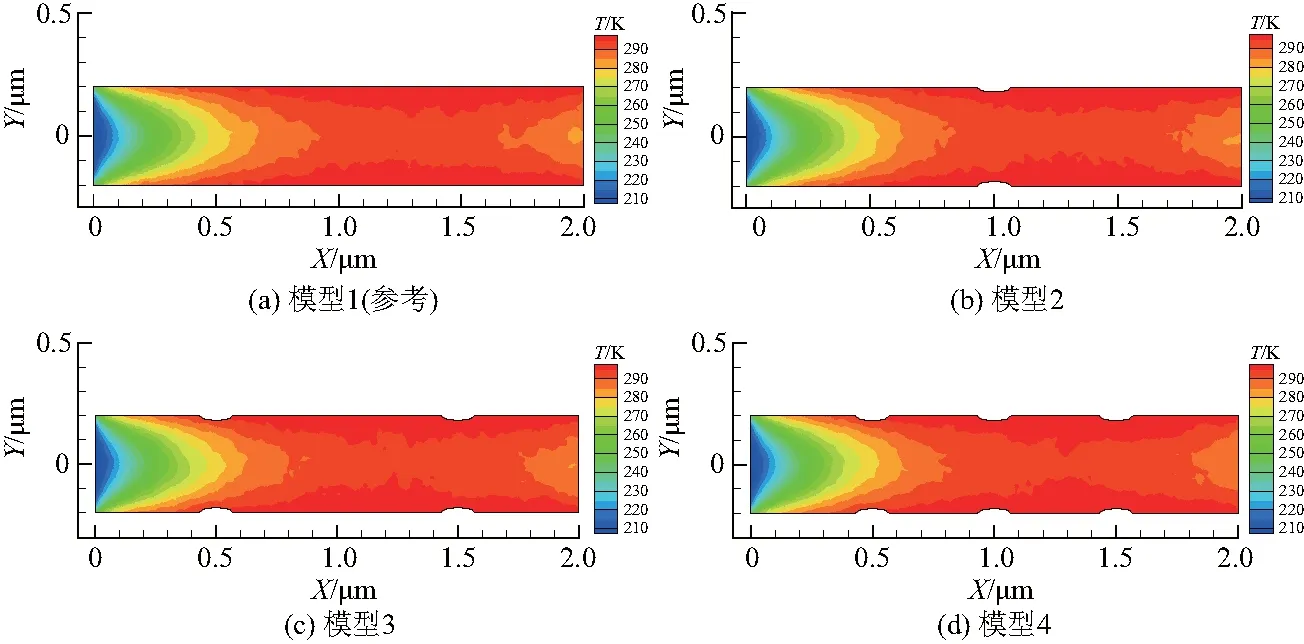
图6 不同结构微通道内流场温度分布Fig.6 Temperature distribution in the microchannels with different structures

图7 不同结构微通道内流场压力分布Fig.7 Pressure distribution in the microchannels with different structures

图8为不同结构微通道流场的特征值分布情况并进行了比较，结果说明了压差驱动下的微通道流动和换热特性变化过程：在流动方向上，壁面压力线性式下降；热流通量呈对数型变化；壁面摩擦阻力受分子热运动影响波动较大，但基本呈线性上升的趋势；通道中心线上的Re数先急速上升后缓慢下降.整体来看，压力和热流通量与粗糙元数量与分布的相关度不大，粗糙元对这两种特征参数的影响仅仅是在其对应的分布位置处产生了相近幅度的波动，各模型中壁面压力和热流通量值总体的变化范围和分布趋势仍基本相同；而固壁表面摩阻和流动中心线上的Re数总体变化范围值则随着粗糙元数量的增加而有所降低，从数值上看，每增加一组粗糙元，固壁表面平均摩阻下降约3%，中心线上的Re数平均值下降约1.5%，而壁面压力和热流通量的平均值变化在1%以内波动，变化幅度比较有限.结果表明，粗糙元分布与数量的变化对整体壁面的流动传热性能影响有限，当单个粗糙元本身结构不变时，其产生的阻滞和压缩效应仅能对微通道内流动与传热性能产生局部影响.另外，随着粗糙元数量的上升，流动受到的正向阻滞不断增多，整体速度随之下降，从而导致壁面摩擦阻力和Re数的整体数值略有降低.

另一方面，从局部来看，粗糙元对各流动参数均会产生波动式影响，但对壁面参数的影响则较为明显，波动峰谷值明显且幅度较大，中心线上的Re数变化则相对较缓；同时，当存在多个粗糙元时，粗糙元产生的特性参数波动沿流线方向逐渐增大，例如模型4中，沿流动方向的粗糙元表面压力波动幅值分别约为2.81×104、3.27×104和3.99×104，热流通量波动幅值分别约为8.05×105、1.75×106和2.34×106等.流动特性参数的计算公式与流动物理量密切相关，因此其波动幅度与该处流场物理量梯度的变化存在关联.结合上文，在粗糙元表面的各物理量中，仅速度梯度沿流线方向不断增加，温度和压力梯度分别为逐渐减小和基本不变，因此可以看出，微通道内的速度梯度是特性值波动的主要影响因素.

综合上述内容可以得出推论：粗糙元对微通道内的流动和换热系数会产生波动式影响，其波幅大小主要取决于局部速度梯度；在流动方面，粗糙元对通道内部流场会产生明显的阻滞效应，但该效应主要是由于粗糙元对正向流动产生了阻挡并导致了局部逆压梯度的出现，从而增大了流动阻力，而壁面粘性并没有因为粗糙元的存在而有所增长，壁面摩擦力整体数值变化范围的下降证明了这一点.在换热方面，由于粗糙元对流动产生的压缩效应提高了局部流速，该位置的热流通量出现了极值，同时，粗糙元增大了壁面与流体的接触面积，该处的换热量明显提高.

图8 不同结构微通道内流场特征值分布Fig.8 Characteristic values distribution in the microchannels with different structures

3.2 粗糙元高度尺寸

以模型4的粗糙元分布结构为参考，通过改变粗糙元的高度来研究其形状尺寸变化所产生的影响.各模型中粗糙元Y方向上的高度分别为0.04、0.06和0.08 μm，其网格结构如图9.

图9 粗糙元高度不同时各微通道模型结构Fig.9 Grids and structures of the microchannels with different heights of rough elements

图10～12为粗糙元高度不同时各微通道内的流场速度、温度和压力分布.图中结果清晰的显示，随着粗糙元高度的增加，其对微尺度稀薄气流的压缩效应越发明显，通道内流场的高速区域逐渐向粗糙元对应的中心线位置集中，例如在模型7中，流场最高速度已离开出口，出现在近出口粗糙元所对应的中心线位置，但与此同时，流动中的正向阻力显著增强，流动速度的下降也较为明显；此外，由于压缩效应逐渐加强，粗糙元表面的流场压力梯度和等值线弧度进一步增大，在模型6和7中，该处已出现了密集的压力渐变等值线簇，而且粗糙元附近的等值线形状和分布也逐渐发生了改变；在温度场中，通道内高温区域不断扩大，入口低温扩散区域逐渐减少，在模型7中，低温来流的温度梯度变化基本被压缩在入口至第一个粗糙元之间，除出口处流体受膨胀作用影响，温度出现局部降低外，其余流场均处于接近壁面温度的状态.结果表明，与数量和分布变化相比，粗糙元高度的增加对微通道内流动和换热状态有着更为明显的影响，边界层结构、等值线形状和分布等均发生了较大改变，进一步证明了粗糙元对微通道稀薄流动的正向作用是影响流场变化的主导因素.

图10 不同结构微通道内流场速度分布Fig.10 Velocity distribution in the microchannels with different structures

图11 不同结构微通道内流场温度分布Fig.11 Temperature distribution in the microchannels with different structures

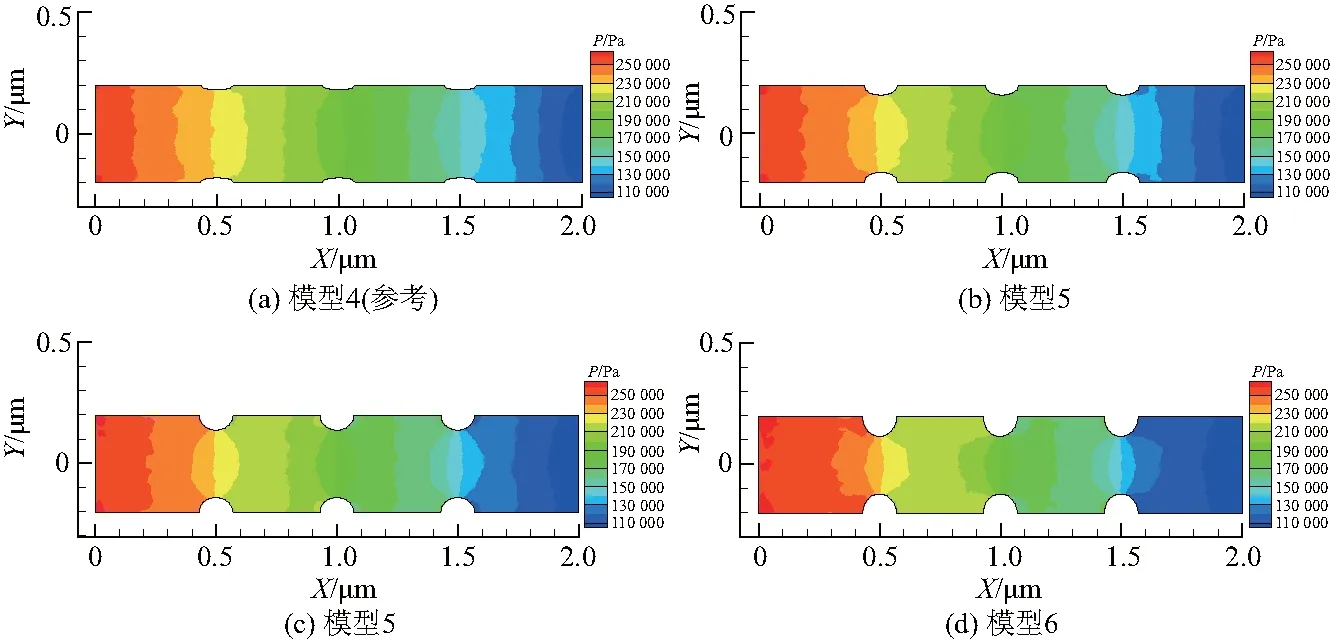
图12 不同结构微通道内流场压力分布Fig.12 Pressure distribution in the microchannels with different structures

图13为粗糙元高度不同时各通道流动和换热特性参数的变化情况.参考图8中的特性参数变化，粗糙元高度变化时微通道内流动和换热特性参数的整体趋势和波动规律与之相比基本一致，而其不同之处为：① 各模型中固壁表面压力和热流通量的数值分布出现了比较明显的差异；② 不同模型中粗糙元之间平直段的壁面摩擦阻力差异较大，除粗糙元分布位置外，其他位置的壁面摩阻呈逐次降低的趋势；③Re数的分布态势和波动幅值均出现了大幅度的变化，粗糙元高度的增加不但使Re数大幅降低，而且使其波动幅值不断上升.

图13 不同结构微通道内流场特征值分布Fig.13 Characteristic values distribution in the microchannels with different structures

从具体数值来看，粗糙元高度每增加0.02 μm，其所在位置处的壁面压力峰值提高约1.5%，热流通量平均值降低约7.7%，壁面摩阻平均值比前一种模型约低20%，Re数平均值降低约10%，其峰值降低约2.4%～6%.结合流场物理量分布的计算结果不难分析得出：粗糙元高度的增长提升了通道内流动的正向阻力，同时也提高了粗糙元对流体的压缩效应，因此，通道内的平均流速明显降低，而粗糙元位置的流场物理量梯度变化大幅上升，进而导致通道内流场的边界层结构发生改变、壁面摩阻和流场中心线上的Re数下降、特性参数的波动幅度增加等变化的发生，流动和换热中的非稳态特征有所增加.

4 结论

针对壁面粗糙元对微通道流动和传热产生的影响问题，采用DSMC方法开展研究，首先通过参考算例验证了方法的有效性，然后通过调整粗糙元的数量、分布位置和高度尺寸，模拟了不同状态下微通道内的流动和换热状态，并分析了粗糙元对微通道流动与换热特性的影响机理，得出以下结论：

(1) 粗糙元对微通道稀薄流动的主要影响在于其对正向来流产生的阻滞和压缩效应，前者使通道内流动速度有所降低，后者则增强了粗糙元位置的物理量梯度，并导致流动和传热特性产生波动，波动幅度与局部速度梯度相关.总体来看，粗糙元能够降低微通道内稀薄流场的流动性，并增强流动中的非稳态特征.

(2) 在传热方面，粗糙元的阻滞效应会降低通道内的气流速度，导致微通道内平均对流换热量降低；但粗糙元表面面积的增加会提高该处的局部换热量，同时受压缩效应的影响，粗糙元迎风面的对流换热量将急剧增大，而随着流动中非稳态特征的发展，流体内部的对流换热也将更加强烈.由此可见，粗糙元对通道壁面的换热量会产生聚集效应，换热性能会在其本身的位置显著增强，但微通道的平均换热性能仍会随着流动速度的降低而下降.

(3) 与粗糙元分布和数量变化相比，粗糙元模型高度的改变能够更加明显的改变通道内的流动和换热特性，这主要是由于粗糙元的高度变化能够将其对流场的阻滞和压缩效应在局部位置放大化，在壁面粘性较弱的微尺度流动条件下，局部效应产生的影响更加明显.