融合随机因子的协方差自适应进化策略

韩束丹，田雨波，李 睿，丁伟桐

(江苏科技大学 电子信息学院， 镇江 212100)

协方差自适应进化策略(covariance matrix adaptation-evolution strategy,CMA-ES)[1]，是演化启发式算法的一种，主要用于解决高维复杂问题，被认为近百年来最为成功的连续黑盒优化方法之一[2].该算法通过扰动其协方差和步长来学习适应度函数的核心特征，从而引导累积步长向全局最优点移动[3]，且在不可分离的高维病态问题上表现良好且具有空间不变特性[4].在其较多的内部参数赋予了算法处理复杂问题能力的同时，如果这些参数值选择不恰当，CMA-ES算法就易出现陷入局部最优、收敛速度慢等问题.为了提高CMA-ES算法的性能，众多学者进行相关的研究与改进.文献[5]提出Cholesky因式分解，将算法的时间复杂度由Θ(n3)降为Θ(n2)；文献[6]提出将协方差矩阵对角化的方法，将时间复杂度和空间复杂度降为线性，大大缩短了算法的时间复杂度；文献[7]解决了引入Cholesky因式分解导致的计算演化路径复杂度过高的问题，显著提高CMA-ES算法在解决非低维度问题上的效率；文献[8]提出一种带有限记忆的协方差矩阵适应进化策略，提高了CMA-ES算法在处理不可分离的高维病态问题上优化速度和处理性能.文中提出了一种带有随机因子的协方差自适应进化策略(random-factor CMA-ES，RFCMA-ES)，通过在全局步长更新时加上具有随机因子的差值项，避免陷入局部最优，能更好地保持进化群体的多样性，从而提高算法全局寻优的能力，并采用6种不同的标准测试函数进行数值仿真，实验结果验证了RFCMA-ES算法在搜索能力、收敛速度方面相比于原始算法有了很大提高.

1 CMA-ES算法及其改进

1.1 CMA-ES算法

在CMA-ES算法中，初始种群规模λ较为关键，λ值选取过小，算法评价数据较少，全局搜索能力弱，易陷入局部最优；λ值选取过大，会引入冗余量，影响算法寻优速率.为了使λ值相对合理，一般使其与问题参数的维数N挂钩，通常取种群粒子数为：

λ≥4+3lnN

(1)

λ值确定之后，便可调用独立于优化算法的适应度函数计算种群中λ个粒子的适应度值，并将其按升序重新排序，选取其中前μ个粒子构成初始种群的子孙种群.

更新后问题参量的各维度期望值:

(2)

Cg决定Bg和Dg，式(3)为Cg奇异值分解：

Cg=BgDg(BgDg)T=Bg(Dg)2(Bg)T

(3)

表1 CMA-ES内部参数计算公式

1秩更新量C1g+1定义为:

C1g+1=c1pcg+1(pcg+1)T

(4)

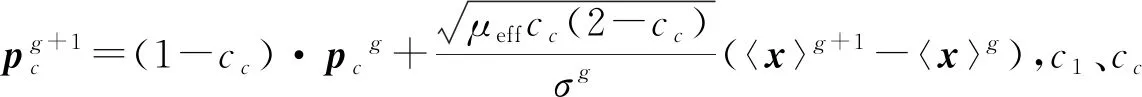
μ秩更新量定义为:

(5)

其中,ωi和cμ的具体意义和计算公式见表1．

总的协方差矩阵Cg+1更新公式为:

(6)

上述的协方差矩阵是去除各维度量钢差异之后的归一化值,最终高斯分布的协方差还会受到方差步长σ的影响．σ值的大小表示了搜索区域粒子各维度参数值调整的幅度,全局步长σg+1的更新公式为:

(7)

式中：dσ为尼阻系数,dσ≈1；cσ的具体意义和计算公式见表1,E‖N(0,I)‖表示N维多元正态分布,具体表达式为:

(8)

(9)

1.2 RFCMA-ES算法

1.2.1 基本原理

文献[9]根据Rechenberg的“MSC”概念上提出了协方差算法的多路径累积步长方法来扩充目标策略控制参数的自适应模型,即在调制策略参数基础上,增加与之相匹配的变异因子变化形成了“CMA-ES”．“MSC”中变异因子是算法在种群寻优更新路径上产生变异的根本原因,但是,通过增加变异强度不能同时解决提高变化速率与选择差异性性能[10]．鉴此,在“MSC”概念、累积步长思想和原始全局步长σg+1更新公式的机理研究上提出带有随机因子新的全局步长更新方程:

(10)

1.2.2 算法流程

Step1: 根据所求解问题各个维度变量的取值空间,确定种群粒子的初始分布空间.

Step2: 利用高斯分布在初始种群空间中随机选择λ个种群粒子,种群粒子每个维度的协方差矩阵来表示各个粒子的高斯分布幅度.

Step3: 被选中λ个种群粒子构成母系种群,根据适应度函数计算其适应度值,并判断种群中是否存在满足停止条件的粒子；如满足条件则转Step6,不满足则转Step4．

Step4: 在λ个母系种群中选出μ个相对最优的粒子构成子代种群,由子代种群的分布结合相应的权重,根据式(2)得出新的期望值、根据式(6)得出新的协方差及根据式(10)更新全局搜索步长,从而获得新的满足高斯分布的样本空间．

Step5: 重复Step2到Step4的步骤,直到得到满足判定停止条件的适应度值．

Step6: 停止算法运行．

2 实验结果与分析

文中通过6个多维多峰测试函数对CMA-ES与RFCMA-ES性能进行全方面对比评价,分为3个部分:① 通过对6个标准测试函数寻最小值过程对改进算法收敛性性能进行评价;② 将每个测试函数独立实验200次对改进算法稳定性性能进行评价;③ 设置相同测试函数的停止标准,对改进算法收敛速度进行评价．

2.1 算法收敛性评价

选用标准6个多峰多维度测试函数Ackley(在解空间中存在大量局部极小值点)、Rastrigin(在解空间内存在大量的正弦凸起极小值点)、Shubert、Shekel、Styblinski-Tang、Powell对优化算法收敛性能进行评价,其测试函数表达式、变量输入维度、变量输入范围、优化算法适应度寻优次数如表2．

图1为两种优化算法寻优迭代图．

从图1(a)可以看出,经过7代迭代后,RFCMA-ES算法的收敛性优于CMA-ES算法;图1(b,c)中,在F2、F3整个迭代寻优过程中,RFCMA-ES算法性能始终优于CMA-ES算法；图(d～f)中,在算法迭代前期,RFCMA-ES算法与CMA-ES算收敛性时高时低,但是最终趋势为RFCMA-ES算法收敛性优于CMA-ES算法,即RFCMA-ES相较于原始算法更具有全局寻优能力,不易陷入局部最优．

表2 标准测试函数相关参数设定

图1 优化迭代曲线Fig.1 Iteration curve of optimization

2.2 算法稳定性评价

RFCMA-ES收敛性能优于CMA-ES算法,但优化算法的寻优结果具有一定偶然性，因此，将6个标准测试函数分别进行200次独立仿真实验,分别记录CMA-ES算法与RFCMA-ES算法的平均最小值、均值和方差值,如表3,具体利用200次重复实验结果的平均方差来验证RFCMA-ES算法较CMA-ES算法在寻优稳定性上是否有一定的提升．从表3可以看出,RFCMA-ES算法最终寻优结果的均值、最小值和方差值均小于或等于CMA-ES算法,尤其针对像F1,F6这样的在解空间中存在大量局部极小值的函数,即RFCMA-ES算法的寻优能力和稳定性较原始算法有较大提高．

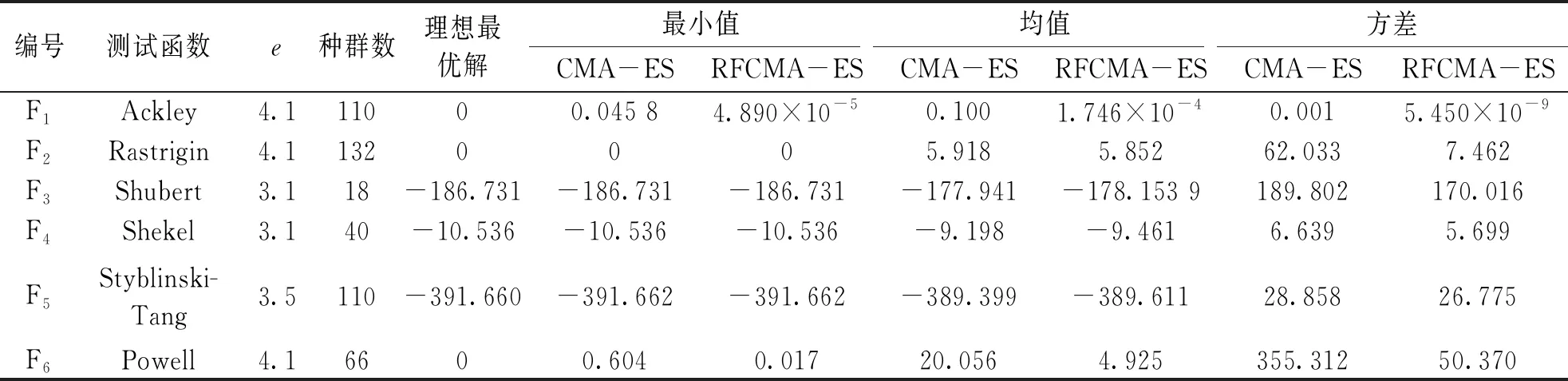
表3 标准测试函数重复200次的平均仿真结果

2.3 算法收敛速度评价

实验PC机处理器为Intel(R) Core(TM) i5-8265U CPU @1.6GHz, RAM为8GB．现在就设置相同停止条件下,对比两种算法应用于6种测试函数的200次平均寻优时间．从表4给出寻优时间可得,RFCMA-ES算法收敛速度较原始算法平均提高36.256%,即所提出的算法较原始算法在寻优效率上有很大的提高．

表4 相同停止条件下标准测试函数重复200次的仿真结果

3 结论

(1) RFCMA-ES算法在原始CMA-ES算法全局步长的更新公式上融合了带有随机因子的差值项,该方法保证了种群个体在进化迭代中彼此之间的差异性,一定程度上避免算法陷入局部最优,有效扩大算法全局搜索范围和提高其寻优效率．

(2) 实验结果可证明,RFCMA-ES算法相比于原始CMA-ES算法具有更加优越的性能,平均收敛速度提升36.256%,且有更强的全局搜索能力．

(3) RFCMA-ES在处理多维多峰问题表现出优越性,将来进一步探索该算法在新领域中的应用,扩展该算法的适用范围,并且将该算法应用到具体工业实际问题的解决中去．